爆炸荷载作用下高速列车车窗玻璃的动态响应
2021-10-31张文岚杜礼明章芝霖李梓豪
张文岚,杜礼明,章芝霖,李梓豪
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)*
在国内外铁路运输系统中,意外爆炸事件以及恐怖袭击对列车的安全运行造成极大威胁.列车侧面爆炸环境下,爆炸冲击载荷主要作用于车体侧墙、车门、车窗玻璃等部位,车窗玻璃在强冲击载荷作用下更容易发生破坏.
在爆炸冲击波研究领域中,辛春亮等[1]根据Henrych、Kinney推导出的爆炸冲击波超压峰值以及正压区段持续时间的经验公式,结合Krauthammer[2]、Martin Larcher等[3]预测得出的冲击波负压峰值以及负压区段持续时间的经验公式,得出球形TNT炸药在自由场中的工程计算模型.廖真等[4]基于AUTODYN软件建立不同装药形状以及类型的近地面TNT的空中爆炸计算模型,研究了马赫波的传播规律以及冲击波参数的变化规律.在夹层玻璃以及玻璃幕墙的抗爆性能研究领域中, Wei,Jun等[5-7]基于弹性力学中的薄板小挠度弯曲理论、大挠度弯曲理论与有限元模拟相结合的方法,对比夹层玻璃的理论挠度与仿真模拟得到的实验挠度,并模拟出玻璃板上的应力分布.P.A. Hooper等[8]在研究爆炸荷载对PVB夹层玻璃的破坏作用时,得出夹层玻璃的破坏原因在于玻璃与PVB胶的分离,并总结出网格大小、不同材料模型以及边界条件对夹层玻璃动态响应影响.张晓颖、李志强等[9-10]研究了爆炸荷载作用下不同的内外层玻璃厚度、PVB夹层厚度、空气层厚度等对夹层玻璃动态响应的影响.邓荣兵等[11-12]利用ALE结合流固耦合算法,研究了爆炸荷载作用下玻璃幕墙的三维动态作用.
目前国内外学者对静态的玻璃幕墙和夹层玻璃的抗爆性能研究较多,而对高速移动的交通工具抗爆性能及车窗破损带来的危害研究相对较少.爆炸冲击波的突出特点为传播速度快、破坏性大,试验测试十分困难且成本巨大,本文采用LS-DYNA软件中的CONWEP计算模型[13-14],结合ALE多物质算法进行仿真分析[15],在2009年俄国客运列车166次“涅瓦特快号”的列车爆炸事故,爆炸产生的威力相当于7 kg TNT.此外高速铁路普遍采用无砟轨道,爆炸装置很难埋藏在轨道下面,相比较于车辆底面爆炸,侧面爆炸更容易发生.美国俄克拉荷马城爆炸案中70%伤亡人员就是由爆炸冲击波对玻璃损伤后产生的高速飞溅碎片造成.考虑列车运行在线路上遭遇爆炸荷载袭击的实际情况,本文以7 kg TNT为爆炸物输入条件,爆炸荷载的模拟采用单点爆炸,研究不同爆距时受载侧车窗玻璃的动态响应,防范这类爆炸(如恐怖爆炸、燃气管爆炸、加油加气站爆炸以及石油化工罐体爆炸等)对列车冲击,为列车在线路上的安全运行与高速列车车窗玻璃的防爆设计提供参考.
1 数值模型与计算方法
1.1 数值模型建立
以某型高速列车二等座车厢的车窗为研究对象,车窗实际采用中空夹层玻璃,结合中空玻璃与夹胶玻璃的特点.车窗总厚度为34.5 mm,中空惰性气体层两侧均为夹层玻璃,玻璃厚度从车体外侧到内部依次为6、4、4、3 mm,共计4层玻璃,夹层为0.76 mm的抗穿透性PVB胶.中空夹层玻璃的结构示意图如图1所示.

图1 中空夹层玻璃结构示意图
车窗内外层玻璃采用目前应用范围较广的MAT_ JOHNSON_ HOLMQUIST_ CERAMICS塑性损伤模型,主要用于对陶瓷、玻璃等易碎材料的模拟;玻璃材料的主要参数为:密度R0=2.53g/cm3,剪切模量G=45 GPa,应变率系数C=0.003,抗拉强度T=0.15 GPa,相对应变率EPSI=1.0,归一化强度SFMAX=0.5GPa,Hugonist弹性极限HEL=5.95 GPa,Hugonist弹性极限上压力PHEL=2.92 GPa,塑性断裂应变参数D1= 0.043、D2=0.85.PVB胶采用MOONEY_RIVILIN_ RUBBER材料模型,在玻璃失效后,PVB胶与玻璃黏结能够增强车窗玻璃的抗爆性能;PVB胶的主要参数为:密度R0=1.1 g/cm3,泊松比PR=0.495,材料常数A=0.0016、B=6e-5.内外层玻璃与PVB胶之间设置带有失效形式的面对面接触来模拟黏结.
车体外部的空气材料以及车窗中空惰性气体层分别采用MAT_ NULL材料模型,并结合线性多项式EOS_LINEAR_POLYNOMIAL状态方程加以描述.假设地面由混凝土、石块等材料构成,可近似看成刚性地面使用刚性壁面来模拟地面.
1.2 数值模拟方法
ALE方法能够直接将爆炸冲击波传递到车体迎爆面上,但模拟计算边界时需要建立从车体外部到炸药的空气域,计算效率低下.仿真过程中为提升计算效率,结合ALE方法与CONWEP计算模型进行爆炸冲击波对车窗玻璃的动态响应模拟,只需要建立车体模型以及包围车体的部分空气域,在CONWEP计算模型中定义爆炸物.需要在ALE算法的外侧设置Ambient Layer,通过Ambient Layer将以CONWEP方法产生的爆炸载荷传递到ALE网格中,图2为Ambient Layer相对车体的位置.
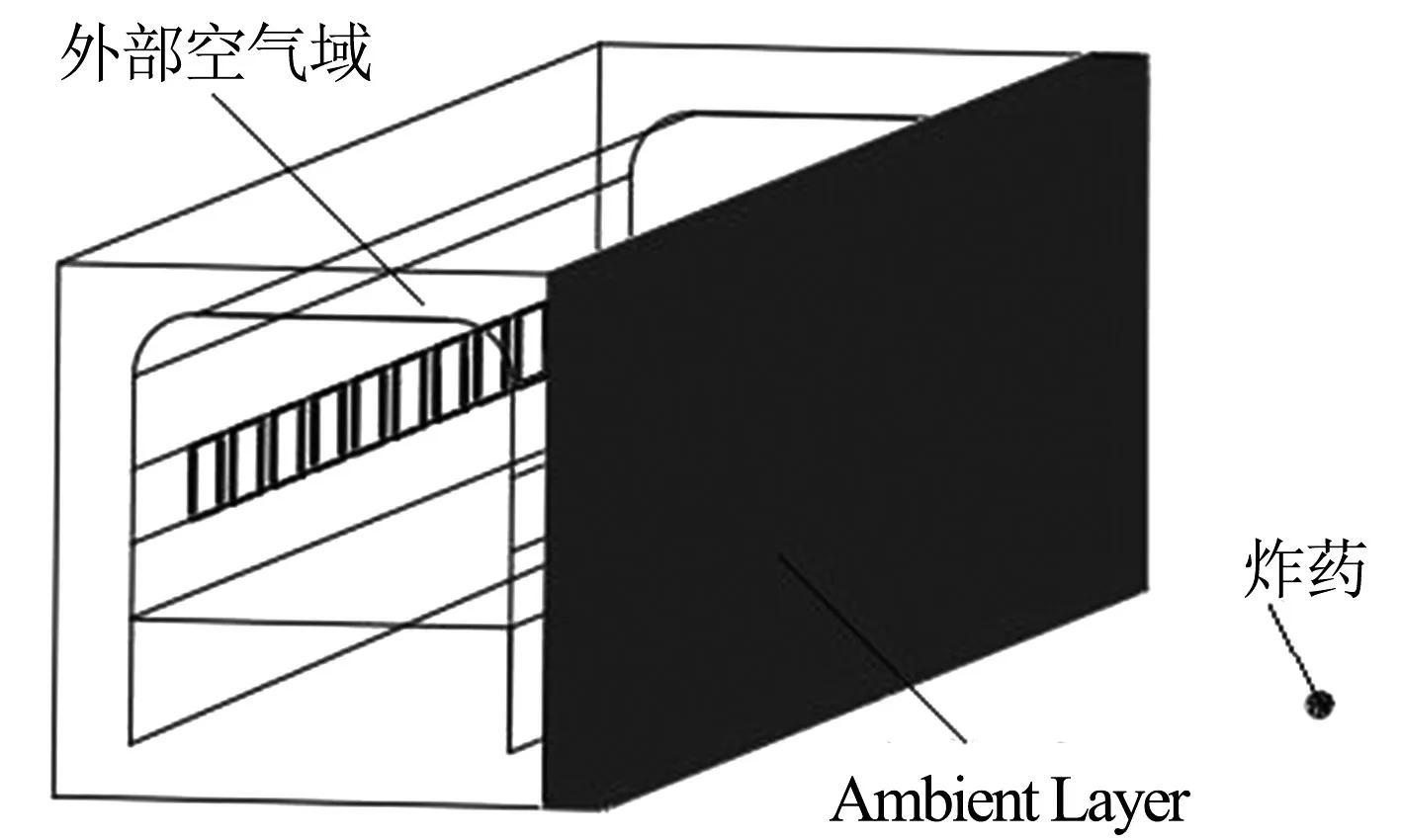
图2 Ambient Layer的建立
车体外部空气域与引入的Ambient Layer 为多物质耦合,分别定义两种单元算法,其中车体外部空气采用单点积分ALE多物质单元,环境单元类型设置为AET=0(非环境),而Ambient Layer也采用单点积分ALE多物质单元,环境单元类型设置为AET=5作为爆炸载荷的受体.建立的外部空气域与Ambient Layer的多物质耦合采用MULTI_ MATERIAL_ GROUP进行界面重构.外层空气域与车体以及车窗玻璃的流固耦合作用采用CONSTRAINT_ LAGRANGE_ IN_ SOLID定义,利用罚函数定义流固耦合.
在边界条件的设置中,通过在车体外部空气域施加无反射边界条件模拟爆炸冲击波向空气场的传播,在模型的边界处通过吸收纵波和横波能量,避免冲击波在边界处反射从而影响爆炸冲击波的传播规律.
2 结果分析
2.1 超压峰值验证
考虑列车运行在线路上遭遇爆炸荷载袭击的实际情况,列车以300 km/h的速度运行在线路上,初步选择炸点的横向位置为距离车体迎爆面4 m处,定义爆炸源类型为近地面爆炸,以7 kg当量TNT为爆炸物输入条件,数值模拟过程中,爆炸荷载的大小直接影响着仿真结果的准确性.分析车窗玻璃的动态响应,首先要保证施加在车体迎爆面上的爆炸冲击荷载的准确性,其中超压峰值是衡量冲击波的重要参数.经过仿真计算,得到车体迎爆面上超压随时间的变化规律.
图3给出了数值仿真过程中爆炸冲击波与车体相互作用的过程,列车以300 km/h的速度运行,由于爆炸时间极短,在t=3.58 ms时,冲击波扩散到车体迎爆面,近地面爆炸后瞬间产生高压,冲击波以半球形向车体传递,此时在车体侧面上超压峰值点为A点(如图3(a)所示),超压峰值大小为886.13 kPa,爆炸产物作用在车体迎爆面上由A点向整个车体迎爆面展开,最终作用在车体以及车窗玻璃上.爆炸冲击波沿车体垂向正方向传播,在车体顶部发生衍射并逐渐消失,所以冲击波超压峰值沿高度方向逐渐减小,同时沿车体纵向的正负方向,冲击波超压峰值也逐渐减小.对照Kingery-Bulmash 经验公式得出的超压峰值为924.28 kPa,冲击波到达时间为3.52 ms,这与采用ALE结合CONWEP方法得出的超压峰值与到达时间基本一致,这种传播特点也符合半球形表面爆炸.由此表明,本文所采用的模拟方法可行.
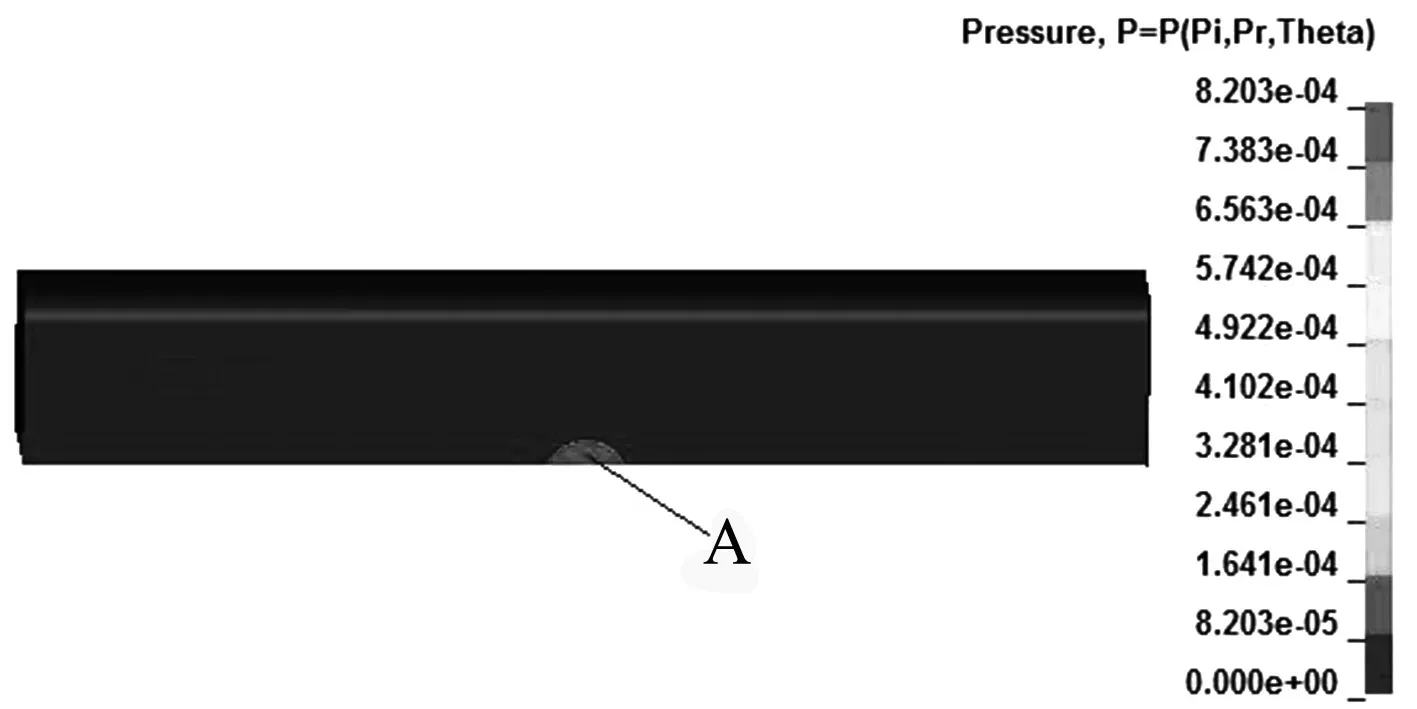
(a) 3.7 ms时超压分布规律

(b) 6.74 ms时超压分布规律图3 典型时刻超压分布规律
2.2 不同爆距下玻璃板心冲击波时程曲线
爆炸荷载作用下,冲击波对车窗玻璃的破坏力主要用冲击波超压峰值来衡量.由于初始时刻,炸药在列车纵向正中间位置,冲击波传递过程中,列车以300 km/h的速度前进了很小一段距离,此时迎爆面上受到最大冲击作用的车窗玻璃为车体纵向中间位置的大窗,而且高速列车车窗采用从外部黏结安装方式,由于车窗的长宽比越大,车窗的安装强度越高,所以高速列车车窗玻璃本身的强度是小于安装强度的,因此不存在由于爆炸冲击波的作用而导致车窗玻璃整体被弹出,车窗与车体之间的连接认为是理想连接,以下模拟过程都基于中间位置的大窗.其中在当量TNT给定的条件下,爆距是影响车体迎爆面上冲击波超压峰值的主要因素,考虑目前高速铁路采用无砟轨道,单线的路基面宽度为8.6 m,车体宽度为3 380 mm,确定距离车体最近的爆距点为2.5 m.图4为不同爆距下车厢迎爆面上超压峰值点,即图3中A点的超压时间历程曲线;图5为车厢受载侧距离炸点最近的车窗外层玻璃板心冲击波超压时间历程曲线,爆距分别为2.5、4、5.5、7、8 m.
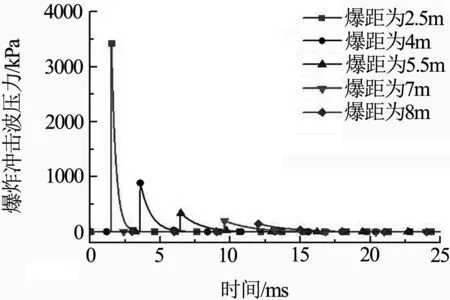
图4 车厢迎爆面上爆炸压力时程曲线

图5 迎爆面上车窗玻璃板心爆炸压力时程曲线
通过分析5组仿真超压峰值对比图可知,炸药起爆位置不同,冲击波随时间衰弱的总趋势基本一致.由图4、图5可见,当爆距为2.5 m时,作用在车体迎爆面上的超压峰值点为3 428.5 kPa,而车窗玻璃板上的峰值点为971.4 kPa,由于炸药放置在地面上,将爆炸类型设置为半球面爆炸,所以冲击波以半球形向车体传递;在冲击波传递过程中,存在正压区段和负压区段,CONWEP计算模块对此负压区段进行了一定的简化,虽然持续时间长,但由于冲击波负压很小,且对车窗玻璃起破坏作用的主要是正压区段,因此负压区段可以忽略.在传递过程中,爆炸产物不断膨胀,波阵面表面积持续增大,此外,在冲击波向车体的传递过程中,还伴随着对空气的绝热压缩,从而产生了部分不可逆的能量耗散,因此,冲击波在空气中的传播不是等熵的.当爆距为8 m时,作用在车体迎爆面上的超压峰值点为145.4 kPa,而车窗玻璃板上的峰值点为125.36 kPa,表明炸药距离车体越近,这种不可逆的能量耗散越多,当炸药距离车体越远,能量耗散越少;爆炸后随着时间的增长以及冲击波在空气中的传播,爆距越长,其正压区越宽.因此炸药距离车辆越近,作用在车体上的冲击波压力值越大,变化速度越快,从而对车窗玻璃的破坏程度也越严重.
2.3 车窗内外层玻璃破坏特征
所研究的车窗采用的中空夹层玻璃具有很高的抗冲击性能,且玻璃板间的PVB胶附着力强,能够在车窗玻璃受到强冲击作用破碎后紧紧附着在PVB胶上,不会飞溅伤人.当爆距为2.5 m时,车窗外层玻璃冲击波超压峰值达到971.4 kPa,内外层玻璃无法承受强烈的冲击波作用而发生破坏,且破坏程度严重,存在大面积的车窗玻璃脱落.在爆炸荷载作用下,为避免单元发生与实际不相符的大变形,考虑车窗玻璃的损伤,将车窗玻璃假设为弹性模型并添加失效准则,定义失效应力的阈值来控制单元失效,当单元失效应变大于阈值,该失效单元将从模型中删除,通过删除失效单元模拟得出内外层玻璃的破坏特征,如图6所示.

图6 车窗内外层玻璃破坏特征
相同当量TNT下,当爆距为2.5 m时,车窗玻璃基本全部脱落.图6为当爆距为2.5 m时车窗内外层玻璃的破坏特征,其外层玻璃最大应力可达到330.4 MPa,内层玻璃最大应力可达到299.1 MPa,远超过车窗外层玻璃的极限抗拉强度,冲击波作用在玻璃上导致几乎所有单元失效从而被删除,外层玻璃破坏后,车窗玻璃的抗冲击性能大大降低.由应力波理论[14]可以得到,当爆炸冲击波传递到车窗内层玻璃上,经过反射会产生同等大小的拉伸波,由于车窗玻璃抗拉强度小于抗压强度,同样导致车窗内层玻璃破坏.
2.4 外层玻璃板心的动力响应
列车在高速运行的过程中,即使没有爆炸荷载作用,内外层车窗玻璃板心也会存在微小振动,本文略去由于列车运行速度导致的车窗玻璃微小振动,分析研究某型动车组二等座车窗玻璃在爆炸载荷作用下外层玻璃板心的位移、速度、加速度历程曲线来衡量其抗爆性能,因此在距离引爆点最近的车窗外层玻璃板中心处分别总结出位移、速度和加速度时程曲线.
分析图7(a)、(b)、(c)得出不同爆距下车窗玻璃在冲击波作用下的振动趋势基本一致.当爆距为2.5 m时,在3.25 ms时板心单元应力瞬间达到其破坏临界值,单元失效;当爆距为4、5.5、7、8 m时,随着爆距增大,其响应速度减慢,位移、速度、加速度峰值越小.
由图7(a)可见,当爆距为4 m时,炸药从起爆时刻开始,经过5.15 ms到达车窗玻璃板中心,在外层车窗玻璃上呈现平面波并迅速向周围扩展,开始产生位移响应,引起车窗玻璃出现振荡现象,在5.15 ms后车窗玻璃板心单元先向车厢内侧运动,并带动四周形成强迫振动,经过8.45 ms左右达到第一个位移峰值点16.9 mm,从起爆后8.45~12.55 ms,车窗玻璃是向外侧振动的过程,此时车窗玻璃变形发生了一定程度的反弹.
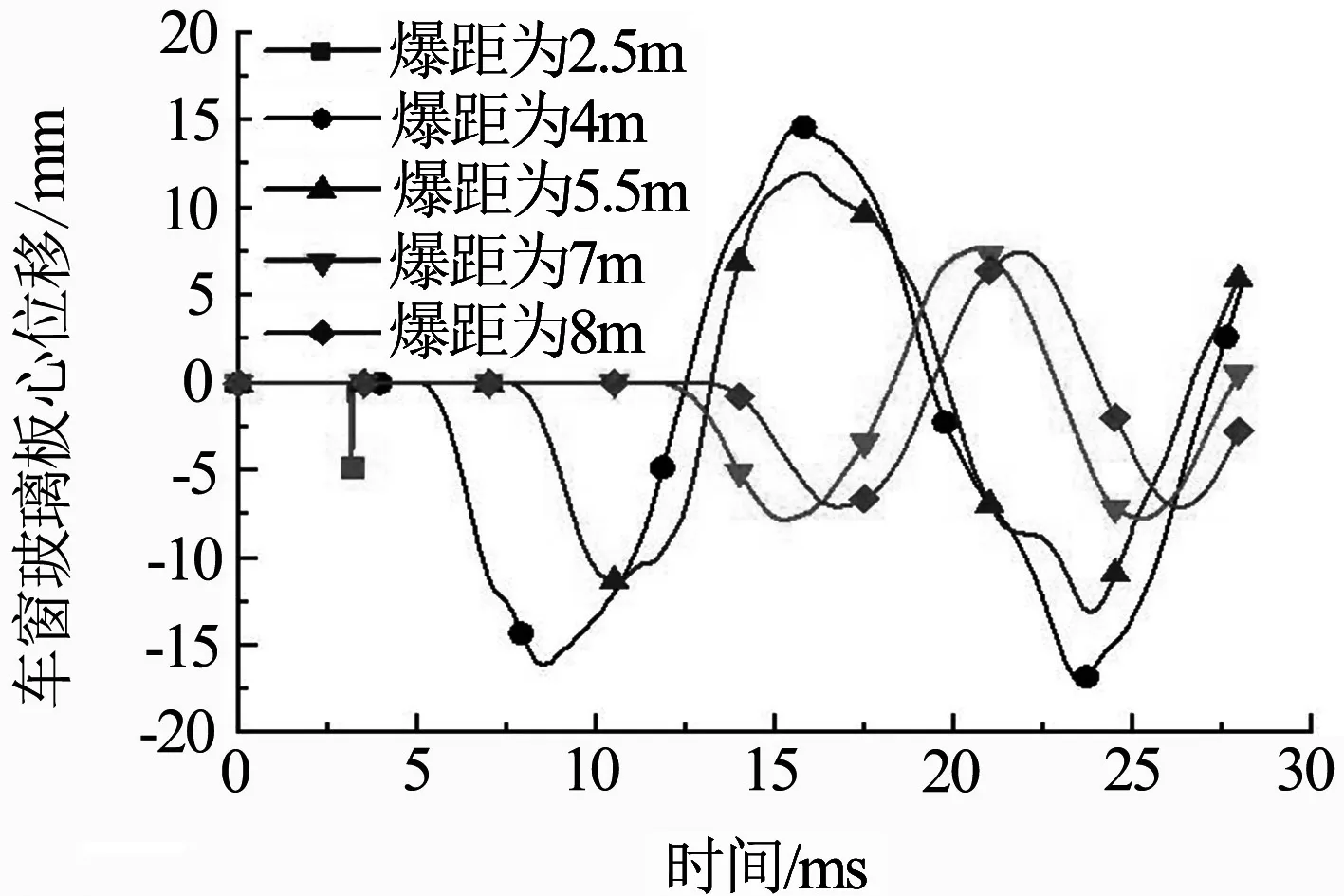
(a) 位移

(b) 速度

(c) 加速度图7 车窗玻璃板心时程曲线
图7(b)为不同爆距下的车窗外层玻璃板中心的速度时程曲线,在相同的TNT当量下,当内外层车窗玻璃未破坏的情况下,爆距越小,其玻璃板心速度峰值越大,振荡越剧烈;爆距越小,响应速度越快.加速度响应也是衡量冲击波做功的重要指标,图7(c)为不同爆距下车窗玻璃板中心的加速度时程曲线,其在爆距为2.5 m时车窗玻璃脱落,加速度响应的最大值为945.5 mm/(ms2),远远大于爆距为4 m及5.5 m等爆距下的加速度峰值,可见,爆距越小,加速度响应的峰值越大,振荡频率越大.
当爆距为2.5 m时,在3.25 ms时刻板心单元应力瞬间达到其破坏临界值时,此时不考虑失效准则,得出不同爆距下车窗玻璃板心的位移峰值、速度峰值、加速度峰值,总结出车窗玻璃板心各个峰值与爆距的关系曲线.
其中位移峰值与爆距离关系的拟合式:
速度峰值与爆距离关系的拟合式:
加速度峰值与爆距离关系的拟合式:
在研究爆炸荷载作用下车窗玻璃板心的位移峰值、速度峰值、加速度峰值与爆距的关系时,通过迭代算法求得拟合函数中的各个参数.其中,各拟合式中最低相关性水平分别大于0.999,拟合度较高,可以根据拟合函数反映车窗玻璃板心各峰值与爆距的关系.车窗玻璃板心位移、速度、加速度峰值与爆距的拟合曲线分别为图8(a)、(b)、(c),根据拟合曲线得出,在保持TNT当量一定时,车窗玻璃板心位移峰值、速度峰值、加速度峰值随着爆距增大呈指数型衰减.

(a) 位移

(b) 速度
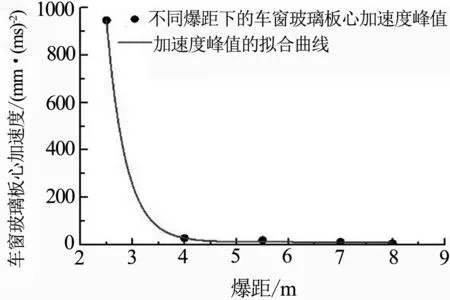
(c) 加速度图8 车窗玻璃板心峰值与爆距关系
3 结论
(1)采用CONWEP计算模型结合ALE多物质算法进行模拟,结果表明:该方法准确高效地模拟了冲击波扩散到车体迎爆面以及在车体顶部发生衍射到逐渐消失的过程,发现车体侧墙上的超压峰值点为886.13kPa,并且不同爆距下车体侧墙以及车窗玻璃上的超压峰值呈指数型递减;
(2) 当爆炸距离较近时,冲击波压力导致内外层玻璃单元发生与实际不符的大变形,通过添加失效准则,删除失效单元得出内外层玻璃大面积脱落的破坏特征;
(3) 研究了不同爆距下车窗玻璃板心的响应指标,得出在TNT当量一定时,车窗玻璃板心的位移峰值、速度峰值、加速度峰值随着爆距增大呈指数型函数衰减,为车窗玻璃的抗爆设计以及改进提供参考.
