方格网法在山地选址问题中的应用

陈雨杉

摘要：随着科技的进步与社会的发展，城市建设对土地的需求越来越大，对于山地城市而言，向山要地更是发展的一个必然选择。其中，工厂的选址更是成为山地城市中的一个焦点问题。本文基于以上背景对该问题进行分析，结合方格网法建立了离散优化模型并进行求解，从而得到不同条件下的满意选址结果。

关键词：方格网法;区域土方平衡;最优分层模型

一、背景介绍

近年来，随着我国经济的不断发展以及人口的迅速剧增，城市建设对土地的需求越来越大。因此，为了满足社会发展的用地需求，人们迫切需要对山地进行开发，尤其是位于城市周边的山区地带则成了人们的首要选择。所以说"开发山地，利用山地"是我们所面对的必然选择。[1]在建设过程中，对于山区城市而言，向山要地更是成为发展的一个必然的选择。

但是如何在一片山地之中选择合适的地域，不仅涉及合适的方位与开挖深度，还需要在挖、填方尽可能平衡的前提下，使工程费用最小。因此，对山区城市的工厂进行合理选址对城市的合理规划与企业的发展起着至关重要的作用。

二、问题的提出及分析

某山区城市的某工厂需在一片长度为1500米，宽度为1000米的山地之中开挖出一个800米×600米平坦连续的长方形地块作为工厂的厂房地基选址，在挖、填方土方量尽可能平衡的前提下，考虑在什么地方，什么海拔高度可以平整一块800米×600米的水平面连片土地，使选址的工程费用最小。

考虑底面区域对应的山体是一个曲顶柱体，根据微积分的知识，可将山地分成n个区域。在底面区域内取一个800米×600米的矩形，建立以矩形左下标点为旋转中心，旋转角度为变量的离散连续方程模型，且在挖、填的土石方量尽可能平衡的情况下，确定合适的高度使选址的工程费用最小。基于方格网法，让底面区域在地面区域范围内枚举，即可计算出对应的土石方量最小的值。

三、模型的假设

①假设除了挖土和填土以外，在平整土地的过程中其他作业产生的费用都与800米×600米的连片土地所处的位置方向和海拔高度均无关。

②不考虑计算体积的过程中，分割的小曲顶柱体不能达到无穷小，取一个很小的步长去划分，使其划分尽可能的小，而产生的误差忽略不计。

③不考虑平整土地后表面的凹凸石块，忽略该局部高度差产生的影响。

四、模型的建立与求解

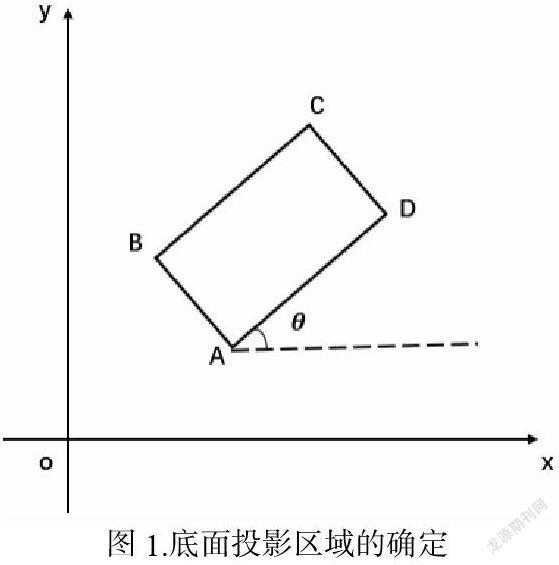
确定开挖方向，即要确定平整块的底面位置。首先，将平整区域投影到底面（XOY平面），显然底面是800米×600米的矩形，假设矩形的四个顶点分别为A、B、C、D。已知山地是长度为1500米，宽度为900米的矩形区域，因此平整块底面投影矩形ABCD可以在1500×900的区域范围内任意移动，但四个顶点不能超出这个范围。

设矩形ABCD的边长AB=W=600，AC=L=800，各頂点的坐标分别为A（xa，ya），B（xb，yb），C（xc，yc），D（xd，yd），沿A点将矩形ABCD进行旋转，旋转角度为θ。已知A点坐标和旋转角度θ，即可确定B、C、D三点坐标。

基于全搜索法的模型求解：在对1500米×900米的区域进行划分时，当步长τ越小时，每一个网格的边长越小，每个小网格对应的海拔高度就越可以用一个值来代替。当τ无限小的时候，每个小网格即可以看作区域上的一个点。所以，在该模型中，τ越小，模型的精度越高。同理，对于旋转角度θ，当旋转角度的递增步长越小，矩形ABCD可供选择的方案就越多，模型的覆盖范围越广，但这将增加算法的时间复杂度和空间复杂度，因此在求解时，我们选取τ=30，ε取0.1%，旋转角度θ依次递增5°进行计算。

Step1：令步长τ为30，对1500×900的区域范围进行划分;

Step2：选取一点A，给定旋转角度θ，计算其余三点坐标，并检查该平整区域D是否符合约束条件;

Step3：遍历所有网格，得到在该区域D中的最低高程h1和最高高程h2，从h1开始，以步长为0.2逐步增加得到H，计算H对应的填挖平衡度，此处取ε=0.1%。若填挖平衡9度小于给定的ε值，则进入下一步;否则，舍弃该H。

Step4：计算符合填挖平衡的H所对应的土方石头量费用，经过比较得到在该区域内的最小费用值和H。

Step5：以步长为10°增加θ，依次计算在该A点符合条件的矩形ABCD的最小费用值和H。

Step6：在约束条件下遍历所有A点，经过比较得到最小费用和对应的H。

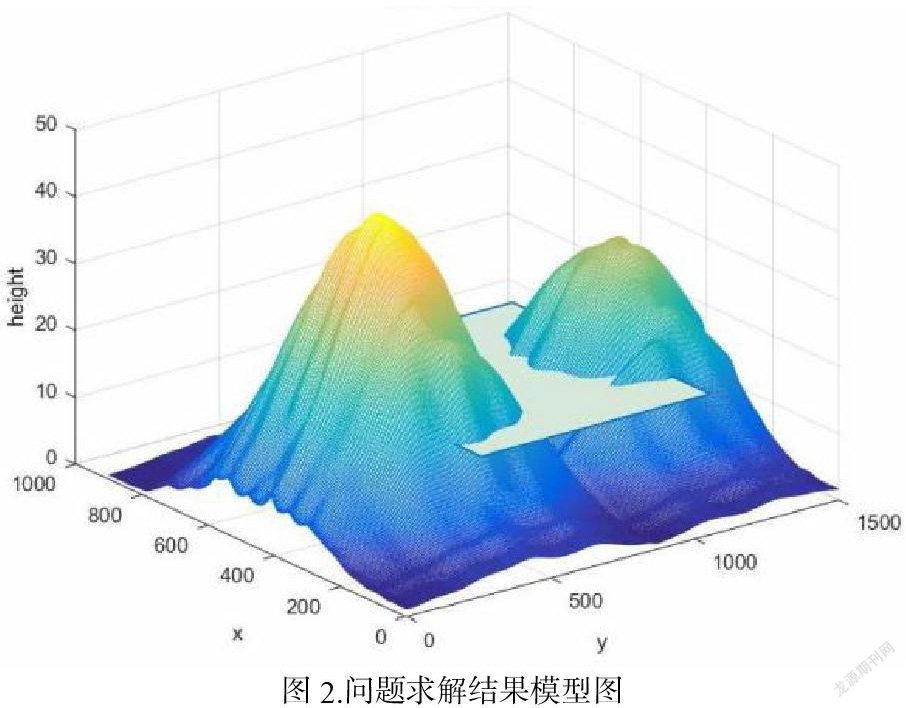
其中各点坐标分别为，A（481，150），B（127.96，219.72），C（1225.66，817.44），D（428.71，747.72），即在以这样的ABCD构成的矩形区域为底面，在海拔h=15.63751米处平整一块800米×600米的连片土地，所需要的土石方量费用最低。

五.灵敏度分析

根据对模型相关参数的分析，我们可以发发现，当τ无限小的时候，每个小网格即可以看作区域上的一个点。所以，在该模型中，τ越小，模型的精度越高。因此我们选取τ为30m、15m、10m、5m依次进行求解，得到的最终挖填差：

由图可以发现，随着步长τ的减小，挖填差的数量也逐渐减少，但填挖和总量增大。步长为5m的搜索结果填挖几乎相同，但总填挖量比其他三个步长的大，填挖差的减小带来了较大的工程量波动，权衡考虑我们选择步长为10m或15m时的结果作为方案。再对角度的搜索步长与挖填差做灵敏度分析，当搜索角度步长从3°减小到1°时，搜索出的填挖差显著下降，从10.84降低至0.24，但同样出现了填挖工程量增大的情况。

六、模型的总结与推广

该模型具有合理性，使用MATLAB软件描述山地的三维图形和等高线图形，在此基础上可以得到具有很高的拟合度和适度性。对模型的进一步讨论便可以得到一系列可靠而实用的信息，所得结论与客观事实很好地吻合，从而进一步说明模型是合理的。

本模型虽然讨论的是以通过土石方量费用最小的原则来确定平整土地海拔的开挖高度，但是可以推广到各种合理开挖土地的问题中，用类似的方法进行建模求解。

解决该问题时，我们首先利用MATLAB软件的三维绘图功能，画出工厂这片土地的三维图形，再确定平整块开挖的方向。本文所建立的模型可以推广到其他各种模型。

参考文献

[1]刘晓梦.论城市周边山区人居环境的保护与开发[D].2013.

[2]范玉忠.散点法与方格网法在土方量计算中的应用比较[J].山西筑，2015，41（32）：194-195

[3]田昌贵，朱志林，肖雪，黄良取，李明，汪振东.三维矿业工程软件优化挖填土石方的方法[J].武汉工程大学学报，2013，35（05）：27-31.

[4]王宁，曹娟.土地整理中坡改梯土方量的计算方法[J].地理空间息，2018，16（06）：112-113+118+9