数形结合思想运用于小学高段问题解决中的案例研究

龚苏梅

摘要：数形结合思想是重要的数学思想之一，即用直观的形表征数的关系、用精确的数表达形的内在特征和规律这样一种思想方法。问题解决贯穿于数学学习始终，数学思想可较为便捷地解决问题。小学高段中遇到较多问题，可运用数形结合思想进行解决，因此运用具体的案例研究小学高段问题解决中的数形结合思想。

关键词：数形结合思想，问题解决，案例研究

1前言

在上世纪，美国的布鲁纳强调了数学思想的重要性，认为用数学思想引领学生进行学习，好处极多，可使得学生的学习变得更简单，更能锻炼学生的总结概括能力，从而增强对其他学科的学习能力。0进入21世纪之后，我国开始重视数学思想，在《义务教育数学课程标准（2011版）》（以下简称《课标》）中，对义务教育阶段的学生提出了要求，要求学生不仅掌握数学基本知识和基本技能，而且要获得数学的基本思想和基本生活经验，0在此处开始强调数学思想的重要性。数学思想直接显现出来的作用是提高数学成绩，还存在一些深层次的推动作用，可帮助思维发展，提高创新能力。有部分人存在一些疑惑，从小学、初中、高中乃至大学都在学习数学，但是这些知识在生活中又不能直接使用，是不是可以不学呢？答案是否定的，学习数学的目的不是在于学会了多少知识，关键在于是否学会了基本的数学思想。

《课标》要求中小学教师渗透数学思想之后，关于如何渗透数学思想的研究逐步火热，一些常见的数学思想再次回归到大众视野，那么数形结合思想也理所当然的再次被人们所重视。所谓数形结合思想，即建立在数形优势互补基础上，抓住数与形之间本质上的联系，以“形”直观地表达数，以“数”精确地研究形的思想方法。0查阅相关文献可知，对于数形结合思想的研究，大致分为如下几类：用以数解形、以形助数、数形相依的方式进行研究;研究整个学段教材中“数与代数、几何与图形、概率与统计、实践与综合”能够体现数形结合思想的内容;利用数形结合思想实际解决数学题目等。在真正的数学学习过程中，问题解决贯穿始终，是数学学习的重要任务之一，却也是部分学生学习数学的重大障碍之一。数形结合思想在问题解决中有着相当丰富的应用，教师若能够利用数形结合思想指导学生，可以帮助学生较好的理解题意，从而快捷、简单的解决问题;学生若能够掌握数形结合思想，则可以将这种思想灵活地运用于解决问题中，当学生看到一大推数字理不清楚头绪时，数形结合思想可以引导学生使用图形的方式表达题意，从而找到问题解决的关键，增强学生学习数学的信心;当图形结构越来越复杂时，学生利用数形结合思想，将复杂的图形结构用已经掌握的数、算式、代数式、方程等进行准确表达，从而提高问题解决的准确性，提升学生数学学习兴趣。

通过文献查询和资料分析可知，数形结合思想有相当重要的作用，而在已有研究中，单纯研究小学高段中数形结合思想的并不多，而又以问题解决为落脚点的研究显得相对更少。因此笔者基于数形结合思想对小学高段的问题解决进行案例研究，希望为一线教师提供一些借鉴和参考，通过课堂中数学思想的渗透，提高教师的课堂教学效果、学生的学习效率。

2案例研究

数形结合思想在各学段、年级均有所涉及，而在小学高段，数形结合思想是使用频率最高的学段之一。在小学高段让学生感知数形结合思想，不仅可以加深学生对基础知识的理解，让学生可以创造性地解決问题，还可以改变学生的思维方式，提升思维能力，让学生更够准确的把握数学关系和规律，提高数学核心素养。那么究竟怎么给学生渗透数形结合思想，让学生明确数形结合的意义和价值，运用具体的案例进行分析是最好的方式。因此本文运用具体的案例分析实际问题中蕴含的数形结合思想，本文中笔者将数形结合思想中以形助数、以数解形这两种具体形式进行案例分析。

2.1以形助数解决问题

进入小学高段，需要解决的问题有更高的难度，要求学生有更高水平的思维能力。虽然小学高段的学生较小学低段学生而言，思维有所进步，但还是比较受局限，因此要让学生掌握一些思想方法，有助于更快捷、准确的解决问题。其中数学结合思想是众多的数学思想之一，运用数形结合思想使得数的特征与形的特征可以相互转化，开阔学生的思路，为学生解决问题提供新方式。

在实际解决问题的过程中，当题目中数量关系过于复杂时，可以利用形进行直观的解决问题;当形过于简单，可以使用数来明确数量关系。0当实际问题过于抽象时，可用画图方式进行直观展示。下面给出一个具体的案例，此案例能够较好的体现以形助数。

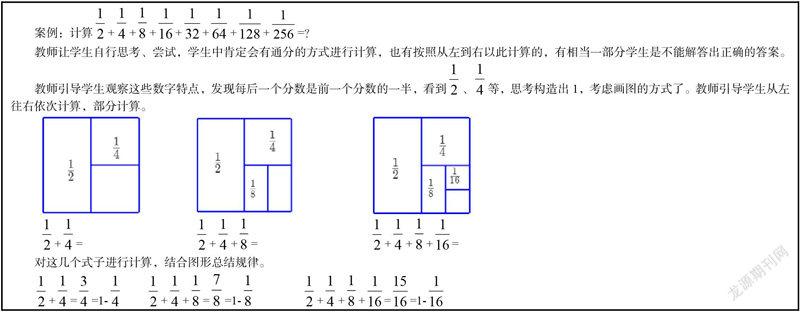
教师让学生自行思考、尝试，学生中肯定会有通分的方式进行计算，也有按照从左到右以此计算的，有相当一部分学生是不能解答出正确的答案。

教师引导学生观察这些数字特点，发现每后一个分数是前一个分数的一半，看到、等，思考构造出1，考虑画图的方式了。教师引导学生从左往右依次计算，部分计算。

对这几个式子进行计算，结合图形总结规律。

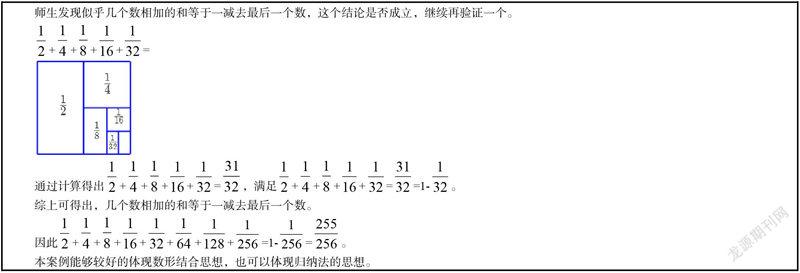
师生发现似乎几个数相加的和等于一减去最后一个数，这个结论是否成立，继续再验证一个。

综上可得出，几个数相加的和等于一减去最后一个数。

本案例能够较好的体现数形结合思想，也可以体现归纳法的思想。

以形助数对于学生解决实际问题有重要的价值和意义。在这里需要我们思考的地方在于若想使用以数助形，必须思考数量关系，找寻到合适的图形来表达数量关系，而找寻恰当的图形对学生有一定的挑战，但是这正是锻炼学生思维的好机会。所以教师在教学中，不仅仅重视对数形结合思想的渗透，让学生能够耐心地观察数量关系，探索内在的规律，从而选择适宜的图形来表达数量关系。同时，教师还要为学生提供足够多的历练机会，使学生能够见识足够多的图形结构，掌握常见的以数助形策略，积累更多的经验，逐步提升应用数形结合思想的自觉性。

2.2 以数解形解决问题

数形结合思想涉及到多方面，不仅仅包括以形助数，还存在以数解形。所谓以数解形，就是看到图形的结构特征，可以找到恰当的数字表达方式，使得图形的特征可以数字化。在实际的学习生活中，遇到以数解形的并不多，因此易被师生所忽视。但是正是由于其稀少性，则教师更应该抓住这种少有的机会锻炼学生，培养学生的思维能力。面对小学生实际的知识储备情况和思维发展水平，应该加强学生用已经掌握的数、算式、代数式、方程等来表示相关图形的特征，使列写出来的表达式子能够恰当的解决相关问题。下文给出两个具体案例，案例能够较好的体现以数解性。

案例：找长方形个数，并给出相应规律。

根据图形找出长方形的个数，得出规律：直接看到n个小长方形，

长方形个数=（1+2+······+n）个。

以上就是以数解形的典型案例，这个案例难度并不大，实际还存在一些稍微复杂的案例，那么在本文中，笔者对一个稍显复杂的案例进行展示。

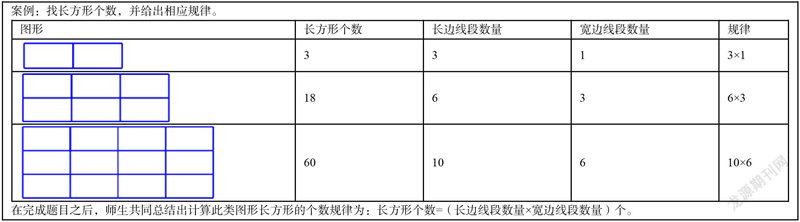
案例：找长方形个数，并给出相应规律。

在完成题目之后，师生共同总结出计算此类图形长方形的个数规律为：长方形个数=（长边线段数量×宽边线段数量）个。

以数解形的方法能够准确表征图形特征，也有利于开拓学生的解题思路。在教育教学中，教师应该为学生挑选恰当的例子，让学生感知以数解形的方式方法。在讲解和探索基础知识过程中，教师应该从多方面寻找数形结合思想相关的素材，给学生体会数形结合思想的机会，帮助学生开阔眼界，拓宽知识面，让学生积累丰富的经验，增强学生对数形结合思想的应用意识，例如遇到判断一个角是否为直角、两边是否相等、图形的周长是多少等类似问题时，让学生明确不仅仅可以直接进行测量，还可以通过计算得出相应结论。0除了教授应该掌握的知识外，教师可以根据学生掌握知识的实际水平，适当拓展一些几何与图形的问题，以此增强学生对数形结合思想的体验，例如去探索一些平面图形边的长度关系，角、周长、面积的大小关系。

3结语

數形结合思想在问题解决中起着重要作用，不仅可以以数解形，也可以以形助数。数形结合思想是一种有效的数学思想，可以发展学生的思维能力。在小学高段的教育教学中，教师引导学生探索基础知识和解决实际问题时，要深度挖掘数与形的本质关系，让学生意识到可以利用直观的形表征数的关系，也可以用精准的数表达形的内在特征和规律。0在学生学习过程中，会多次见识到数形结合的典型例子，学生需多加积累，进行归纳总结，在头脑中形成数形结合的概念，在实际解决问题时，形成自觉利用数形结合思想的习惯。

参考文献

[1]布鲁纳.上海师范大学外国教育研究室译.教育过程[M].上海：上海人民出版社，1973.

[2]中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2012.

[3]邵光华.作为数学认为的数学思想与方法[M].上海：上海教育出版社，2009.

[4]张艳红.数形结合思想在小学数学教学中的应用[D].山东师范大学，2016.

[5]王永春.小学数学与数学思想方法[M].上海：华东师范大学出版社，2014.

[6]陈蕾.让小学生感受“数形结合”的教学策略[J].上海教育科研，2016（02）：83-87.