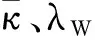一种新型非对称五自由度混联机器人的尺度综合

董成林 刘海涛 杨俊豪

1.中国核动力研究设计院核反应堆系统设计技术重点实验室，成都，6100412.天津大学机构理论与装备设计教育部重点实验室，天津，300354

0 引言

近年来，一类由三自由度1T2R(T表示平动，R表示转动)位置型并联机构和二自由度A/C转头组成的高性能五自由度混联机器人越来越受到工业界和学术界的关注。这类机器人在灵活性、可重构性，以及速度、精度、动态特性等方面，不同程度地继承或弥补了数控机床和关节型机器人的优点或不足，是两种装备技术结合的产物[1-2]。采用该类机器人搭建的机器人化加工装备正逐渐成为航空航天、核能、船舶等高端制造领域大型结构件现场短流程、高柔性、高效率制造的一种重要技术选择[3-5]。目前，这类高性能混联机器人的典型代表有Trciept机器人[6]、Exechon机器人[7]和TriMule机器人[8]等。

尺度综合是实现机器人本体工程设计的关键步骤，涉及根据运动学、静刚度或动力学等性能评价指标优化机构的尺度参数。长期以来，一些学者围绕机器人机构的尺度综合开展了大量的研究。基于运动学性能的优化设计是最为常用的方法之一。该方法一般以反映工作空间能力，以及关节与操作瞬时运动/力传递特性的指标作为目标函数和/或约束条件，以归一化的尺度参数为决策向量开展设计。所涉及的传递特性指标通常为采用雅可比矩阵的代数特征(行列式、条件数、奇异值等)来构造的各种局部和全域评价指标[9-12]。注意到仅当位姿耦合并联机构的雅可比矩阵具有齐次量纲时[13]，其代数特征才能作为正确评价机构运动性能的指标。为此，一些学者先后提出可构造并联机构齐次量纲雅可比矩阵的方法，如特征长度法[14]、特征点法[15]、转动/平动最大灵敏度法[16]等。然而，特征长度法将灵活度在齐次空间中最优的一组量纲一D-H参数作为特征长度，对雅可比矩阵作归一化处理，但因缺乏明确的物理意义而鲜被采用。特征点法是用动平台上若干特征点的线速度来表征操作速度，虽简单直观，但尚无选择这些点的普适性准则可资利用。转动/平动最大灵敏度法物理意义明确，但在优化设计中面临如何选择权重的问题。鉴于上述原因，由BALL[17]提出的虚系数发展而来的传递率已成为评价位姿耦合并联机构运动学性能的主流方法。虚系数被定义为作用在动平台的力旋量在相应运动旋量上所做功的归一值，其几何意义可以被理解为二者螺旋轴夹角的余弦。这类指标包括传递因子、传递指标、传递率、广义传递指标等。它们的共同之处是量纲一化且与坐标系的选择无关，取值越大则运动/力传递特性越好，而主要区别在于归一化方法不同，以及对驱动-约束、串联-并联等特征的细分。近年来，基于虚系数的各种指标被广泛应用于位姿耦合并联机构的运动学优化设计[18-22]。

本文面向大型结构件现场加工的需求，提出一种新型非对称五自由度混联机器人，以期为高性能机器人化加工装备的搭建提供又一可资利用且具有工程实用价值的构型。以其中三自由1T2R并联机构为研究对象，在运动学分析及借助旋量理论构造出量纲一雅可比矩阵的基础上，开展该机构尺度综合方法研究，旨在获得一组使该机器人兼具优良的运动/力传递特性及大作业空间/机构占地比，且具有近似面对称性能的尺度参数。

1 系统描述

图1示出了本文所提出新型非对称五自由度混联机器人的CAD模型。该机器人由三自由度1T2R位置型并联机构和二自由度A/C转头串接组成。其中，前者为R(RPR&RP)&UPS并联机构，包含一条无约束UPS主动支链，和一个由一条RPR支链、一条RP支链组成的1T1R平面并联机构，且该平面并联机构的连架杆件(即转动支架)通过一对连架R副与机架连接。其中，R、U、S分别表示转动副、虎克铰和球铰，P表示主动移动副。在三个P副的驱动下，1T2R并联机构的末端动平台可做绕连架R副的转动，以及RP支链中R副的转动和P副的平动，具备实现大作业空间/机构占地比的能力。动平台上串接的A/C转头则可进一步实现末端执行器的姿态能力。

图1 新型五自由度混联机器人CAD模型Fig.1 CAD model of the novel 5-DOF hybrid robot

上述机器人继承并有机融合了Exechon机器人和TriMule机器人的优点，其特色主要如下：

(1)与Exechon、TriMule机器人中的1T2R机构相同，并联机构由空间支链和平面运动链组成，故仅采用两组占地很小的轴承座作为静平台即可，从而大幅减小模块质量、降低制造成本。此外，转动支架上集成了连架R副，以及RPR支链、RP支链与转动支架连接的R副，是一个二合一构件，故可采用精密立加或精密坐标镗一次装夹加工完成全部孔系加工，保证整机的装配精度和效率。

(2)与TriMule机器人类似，可在A/C转头转轴输出端，R(RP)支链的三个关节上安装圆光栅与直线光栅，故具备实现全闭环反馈控制的功能。同时相较于TriMule机器人，该机器人中平面并联运动链减少了一条从动支链，铰链自由度数目更少，结构更加简单。

(3)相较于Exechon机器人，该机器人中空间支链为六自由度无约束UPS支链，仅承受拉压载荷，容易实现轻量化设计，且装配工艺性更好。

(4)与Exechon和TriMule机器人类似，根据其结构紧凑、可重构能力强的优点，可搭建出形式多样的机器人化作业单元和移动工作站。

值得指出的是，不同于Exechon和TriMule机器人，该机器人中的三自由度1T2R并联机构具有非对称结构，而这一结构特点将导致其工作空间受到限制，同时影响机构受力[23-25]。因此，为了有效避免非对称结构对工作空间的影响，同时获得近似面对称的性能，必须合理设计该并联机构的尺度参数。

2 位置逆解分析及量纲一雅可比矩阵构造

2.1 坐标系建立

为了便于描述，现将UPS支链记为支链1，将转动支架与RP支链(RPR支链)构成的UP运动链(UPR运动链)记为支链2(3)。据此，令点Bi为支链i连架U副的中心，点A1、A2和A3分别表示支链1中S副中心、支链2轴线与动平台平面交点，以及支链3中R副中心，点B和A则分别为B2B3和A2A3的中点。其中，点Bi和Ai分别构成等腰三角形ΔB1B2B3和ΔA1A2A3，如图2所示。此外，又令sj,i表示支链i中第j个单自由度关节轴线的方向矢量，它们满足如下关系:

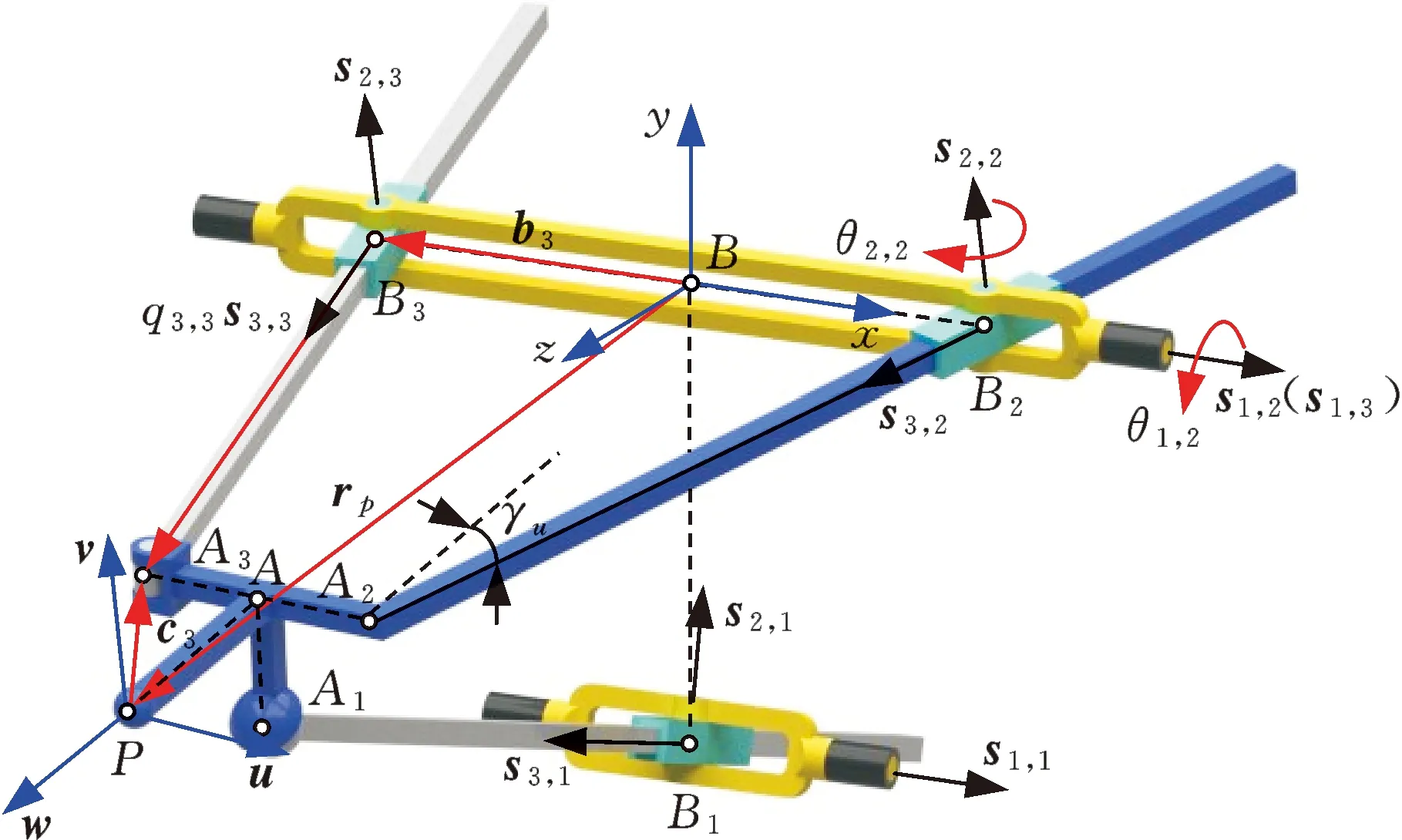
图2 R(RPR&RP)&UPS并联机构的结构简图Fig.2 Schematic diagram of the R(RPR&RP)&UPSparallel mechanism

(1)

为了不失一般性，在点B和动平台参考点P(A/C转头两转轴交点)上分别建立固定参考系B-xyz和连体参考系P-uvw，且满足y⊥B2B3、z⊥ΔB1B2B3，v⊥A2A3、w⊥ΔA1A2A3。注意到UP支链为恰约束支链，故系B-xyz首先绕s1,2轴转动θ1,2，然后绕s2,2轴转动θ2,2+γu即可得到参考连体系P-uvw。据此，参考连体系P-uvw相对于参考连体系B-xyz的姿态矩阵可用关节转角θ1,2和θ2,2表示为

R=Rot(s1,2,θ1,2)Rot(s2,2,θ2,2+γu)=[uvw]=

(2)

其中，c=cos，s=sin；γu为支链2相对于动平台的方位角，即支链轴线与动平台平面法相的夹角，如图2所示；u、v、w分别为参考系P-uvw三个正交轴的单位矢量。

2.2 位置逆解分析

位置逆解分析是R(RPR&RP)&UPS并联机构量纲一雅可比矩阵构造、性能分析及优化设计的重要基础，涉及已知机构的尺度参数，末端参考点P的位矢，求解各支链的杆长。

如图2所示，在参考系B-xyz下，动平台参考点P的位矢rP=(xP，yP，zP)T可表示为

rP=bi+q3,is3,i-ci

(3)

bi=bi(cosφi,sinφi,0)Tci=ai-ew

ai=Rai0ai0=a(cosφi,sinφi,0)T

b1=byb2=b3=bx

q3,i=BiAibi=BBi

a=AAie=AP

根据机构中运动副轴线的布置，存在

(4)

(5)

λ1=xP-bxλ2=yPsinθ1,2-zPcosθ1,2

λ3=acosγu-esinγu

据此，可求解得到

(6)

在此基础上，可构造出姿态矩阵R，进而确定

(7)

2.3 量纲一雅可比矩阵构造

雅可比矩阵表征了关节空间与操作空间之间的瞬时运动/力传递特性，故雅可比矩阵的构造是机构运动学性能评价和优化设计的必要前提。

注意到UPS支链为六自由度主动支链，它仅对动平台提供一个沿轴向的驱动力旋量ξWa,1。而连架R副与平面并联机构组成的R(RPR&RP)平面混联运动链除提供两个分别沿支链2和3轴向的驱动力旋量ξWa,2和ξWa,3之外，还提供机构所需的整个约束力旋量系。如图3所示，根据约束力子空间与许动运动子空间互为零化子空间的原理，该约束力旋量系可分解为：①由UP支链提供的约束力旋量ξWc,1用于限制动平台在面内沿n1,2方向的平动；②由平面混联运动链中两条支链共同提供的约束力ξWc,2和ξWc,3，前者用于限制动平台沿s2,2方向的平动，后者用于限制动平台绕n3,2=s1,2×s2,2方向的转动。

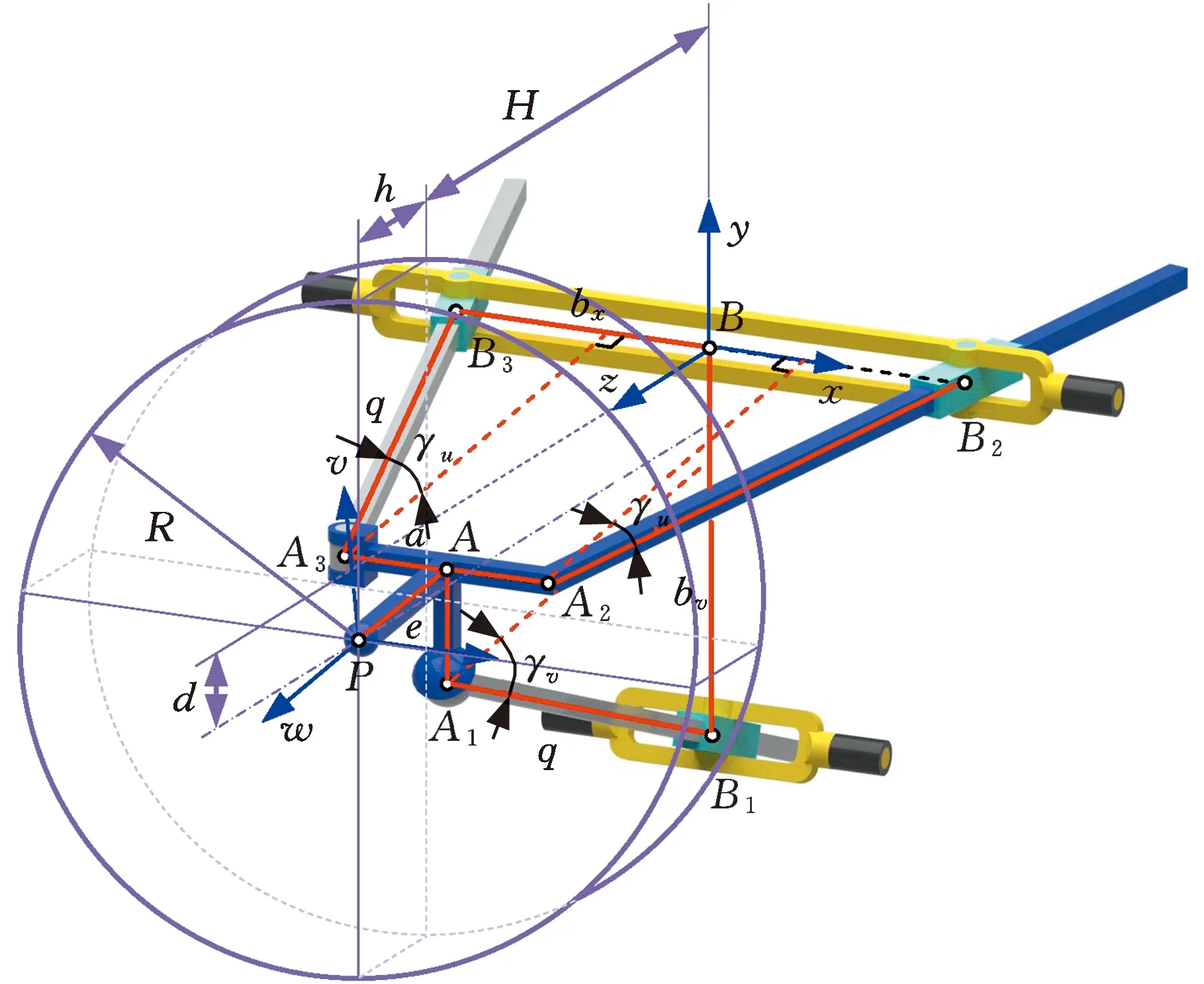
图3 R(RPR&RP)&UPS并联机构的参考位形Fig.3 Reference configuration of the R(RPR&RP)&UPSparallel mechanism

因此，根据驱动/约束力旋量在从动关节上不做功的原理，可构造出动平台关于点P的运动旋量ξt=(δT,εT)T与驱动关节变分之间的雅可比矩阵映射矩阵：

(8)

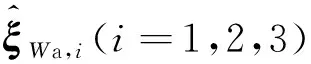
注意到R(RPR&RP)&UPS并联机构为一位姿耦合机构，故ξt的6个Plücker坐标中仅有三个是独立的。因该机构为位置型1T2R机构[2, 26]，不妨取δ为主坐标、ε为副坐标，则按主副坐标对W分块后，可将式(8)改写为

(9)

式中，Waf(Wcf)、Waτ(Wcτ)分别为由Wa(Wc)的线性部、角性部构成的3×3矩阵。

由上式可解出

(10)

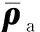
3 运动学性能分析

并联机构的运动学性能主要体现在任务空间/机构占地比，以及运动/力传递特性两个方面，它们可用于构造尺度综合中的目标函数和/或约束条件。本节提出一种凝练R(RPR&RP)&UPS并联机构尺度参数及求解任务空间参数的方法，并定义可定量描述运动/力传递特性及其面对称程度的指标，进而揭示尺度参数对运动学性能的影响规律，旨在为尺度综合提供理论指导。

3.1 尺度参数凝练与任务空间定义

考虑到并联机构一般集中在可达空间中心附近区域工作，因此首先定义三条支链达到各自行程一半的位形为参考位形，如图3所示，则

(11)

式中，q3,imax、q3,imin为支链i的最大、最小杆长。

为了获得近似面对称或轴对称的性能，限定三条支链的最大/最小杆长相等(即q3,imax=qmax，q3,imin=qmin)，且在参考位形下支链3的方位角与支链2的方位角γu相等。据此，不难发现在参考位形下，v-w坐标平面与y-z坐标平面重合，如图3所示。此外，记q3,imean=q、支链1的方位角为γv。

现不妨选取支链行程Δq=qmax-qmin，行程与最小杆长之比μ=Δq/qmin，动平台半径a，以及参考位形下的支链方位角γu和γv为独立的尺度参数，则根据图3中的几何关系，可将其他参数表示为上述参数的函数：

(12)

考虑到R(RPR&RP)&UPS并联机构的可达空间为一非规则几何体，现定义其中的一内接圆柱体作为任务空间，记为WT。如图3所示，WT的半径和高分别为R和h，距离静平台平面高度为H，其轴线与z轴的距离为d，且WT底面的中点对应于所定义的参考位形。现提出一种确定上述参数的数值方法。首先，根据参考位形的定义可确定

(13)

其中，ψ=arccos((qcosγu-qcosγv)/by)表示平面并联机构运动平面与静平台平面的夹角。其次，若by≥bx(或γv≥γu)，且令WT上平面与支链最小杆长约束边界曲面相切，则H取决于支链2的最小杆长，满足

H=

(14)

在此基础上，可进一步由式(13)确定出h。最后，因R取决于支链最大杆长约束，故在q3,i=qmax所约束曲面与z=H+h平面的交线上搜索到点(0，-d，H+h)T的最小距离，该值即为WT的半径R。

3.2 运动学性能指标

任务空间/机构占地比是位置型1T2R并联机构的重要运动学性能指标之一，它反映了用占地较小的机器人模块实现大范围作用的能力。在此，定义R(RPR&RP)&UPS并联机构的任务空间/机构占地比为

(15)

式中，S为ΔB1B2B3的外接圆面积。

运动/力传递特性取决于机构的雅可比矩阵，是并联机构设计必须重点考虑的性能。通常以量纲一雅可比矩阵J条件数的倒数作为评价机构运动/力传递特性的指标，即

(16)

式中，σmax(J)、σmin(J)分别为J的最大和最小奇异值。

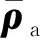
此外，为了反映机构运动学性能的面对称程度，又定义如下指标：

(17)

式中，κ+、κ-分别表示在y-z坐标平面右侧WT中某一给定点，以及该点关于y-z平面对称点所对应位形下的局部运动/力传递特性。

3.3 尺度参数对运动学性能影响规律

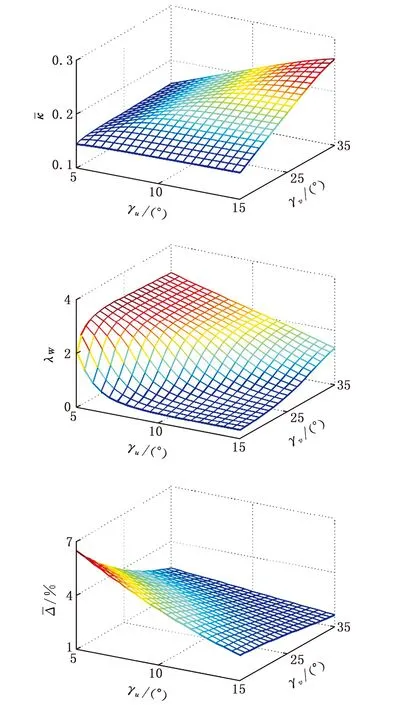
图和随γu 和γv的变化规律Fig.4 Variations of λW and versus γu and γv

4 尺度综合

(18)

在此，xj,min和xj,max表示xj的下界和上界，D={x|c(x)≤0}表示在满足约束条件下决策向量x的可行域。

采用2-范数定义偏差函数并引入权重，进而可将问题(18)改写为

(19)

式中，wi为度量第i个目标重要程度的权重，且满足w1+w2=1。

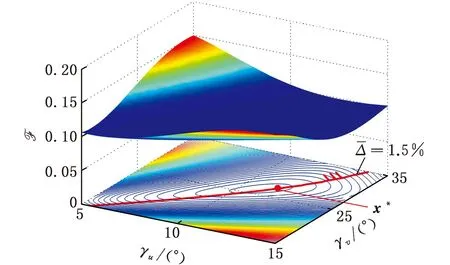
图5 F随γu和γv的变化规律Fig.5 Variations of F versus γu and γv

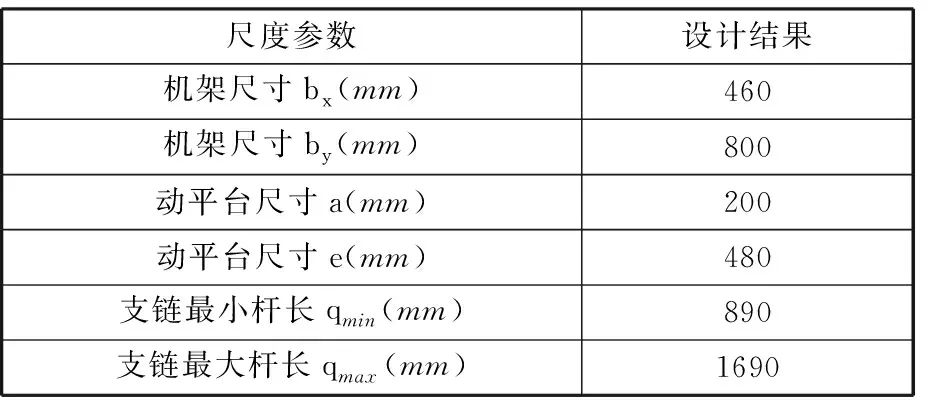
表1 R(RPR&RP)&UPS并联机构尺度参数设计结果

表2 任务空间参数

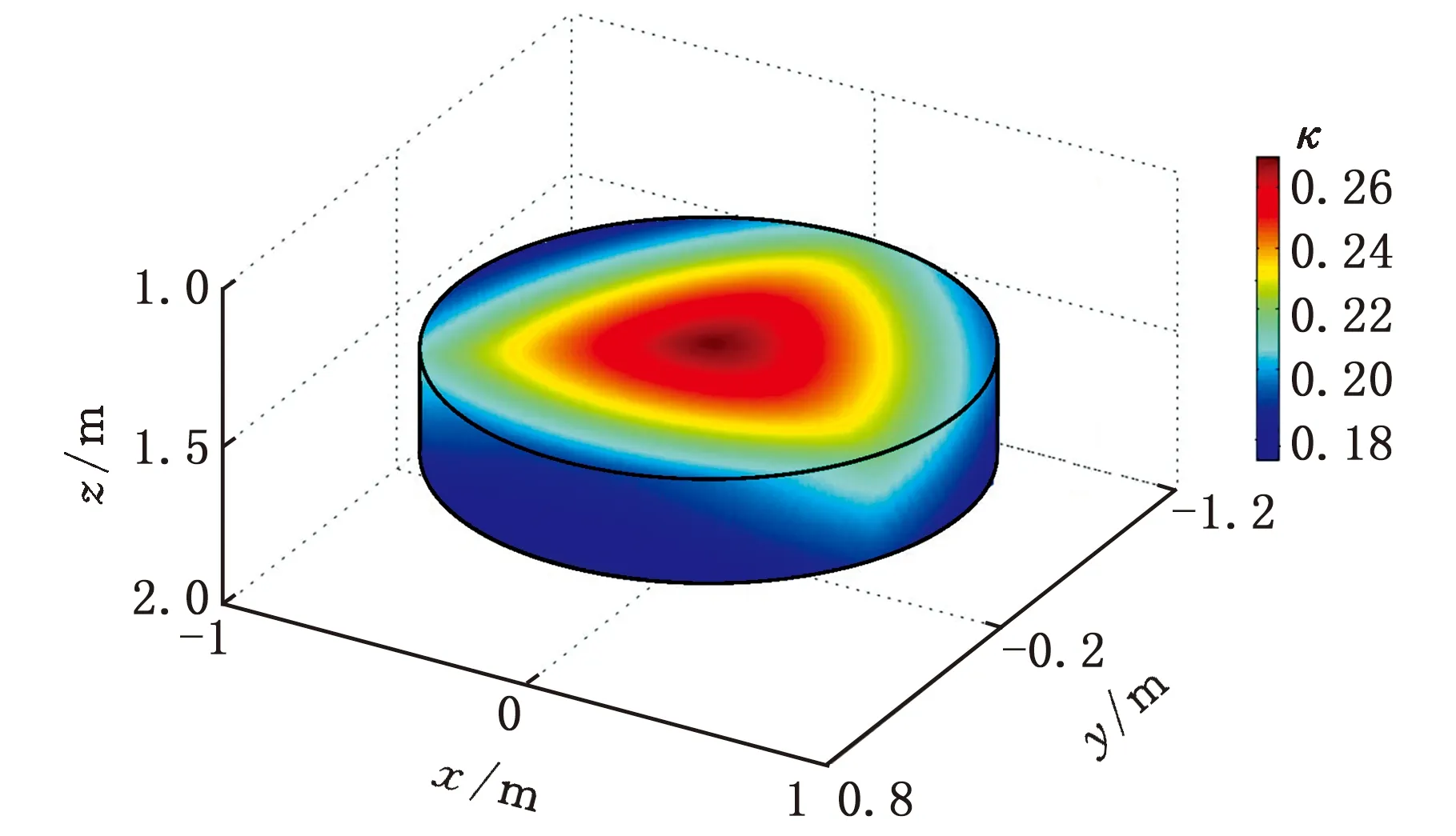
图6 κ在WT中的分布规律Fig.6 Distribution of κ within WT

在同尺度参数下，现将R(RPR&RP)&UPS并联机构的运动/力传递特性与TriMule机器人中R(2-RPR&RP)&UPS机构(图7a)、Exechon机器人中R(2-RPR)&SPR机构(图7b)进行对比。二者的运动学建模及量纲一雅可比矩阵构造分别参见文献[12]和文献[27]。

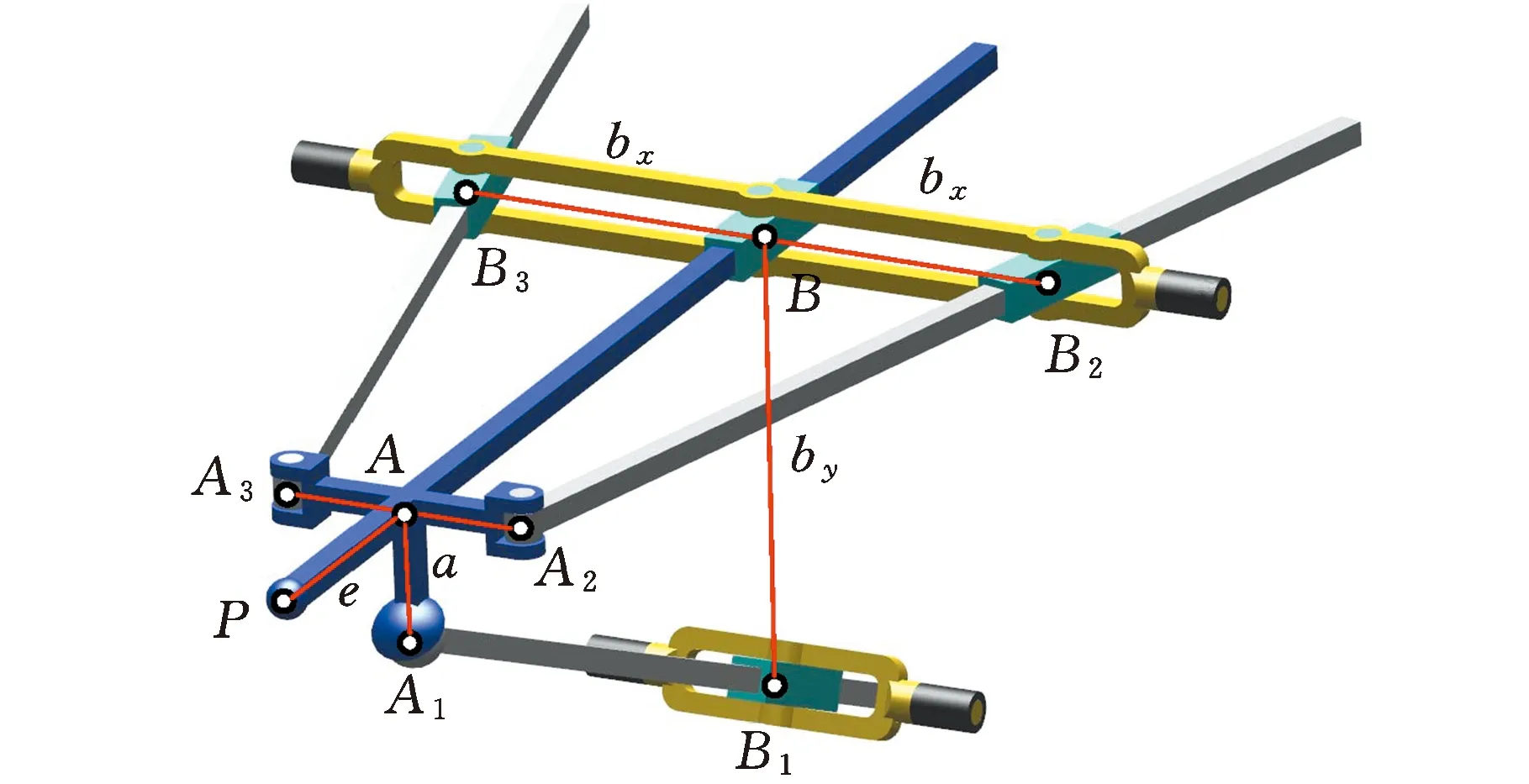
(a)R(2-RPR&RP)&UPS

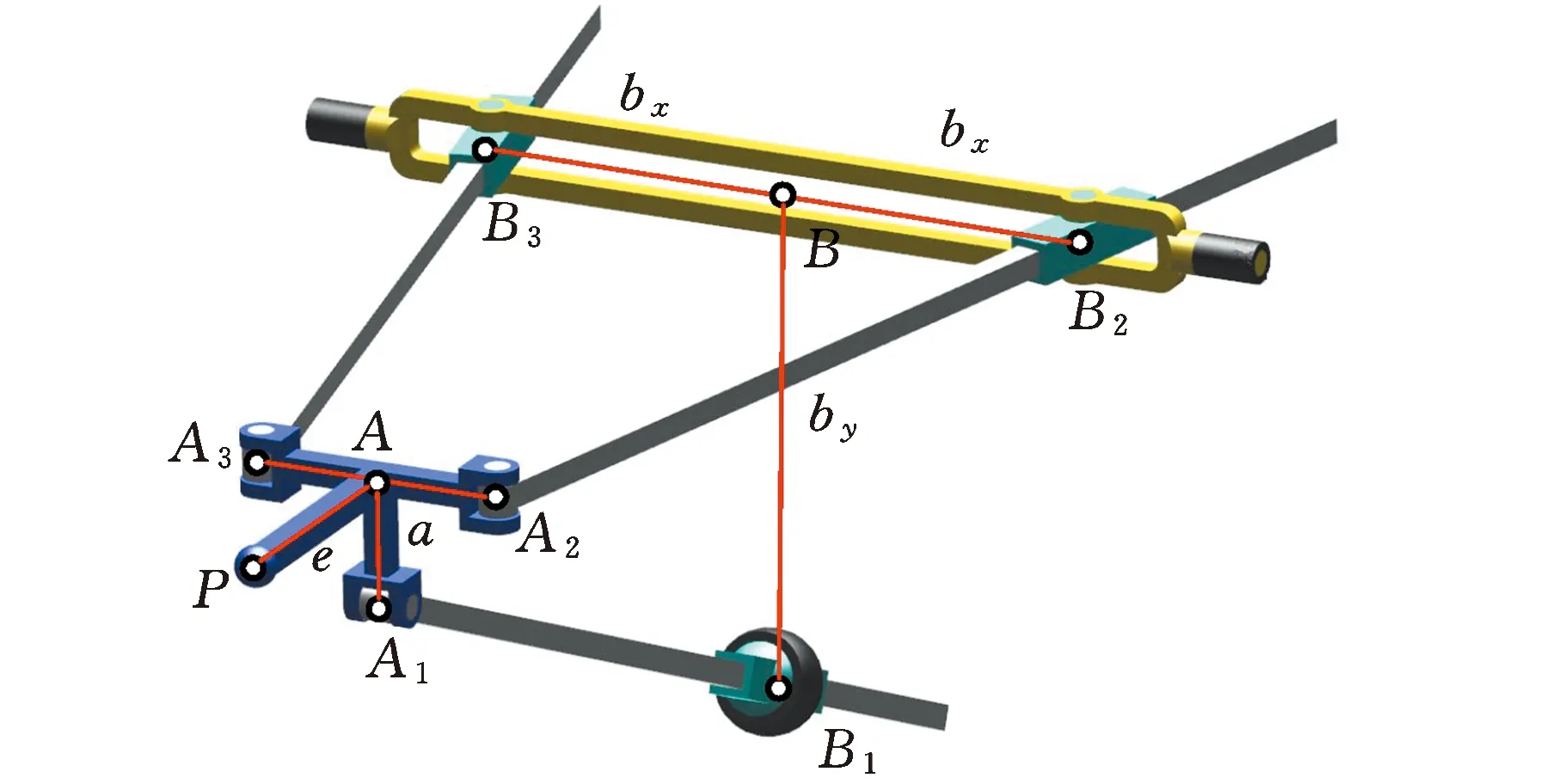
(b)R(2-RPR)&SPR图7 R(2-RPR&RP)&UPS与R(2-RPR)&SPR并联机构的结构简图Fig.7 Schematic diagram of the R(2-RPR&RP)&UPSand R(2-RPR)&SPR parallel mechanism

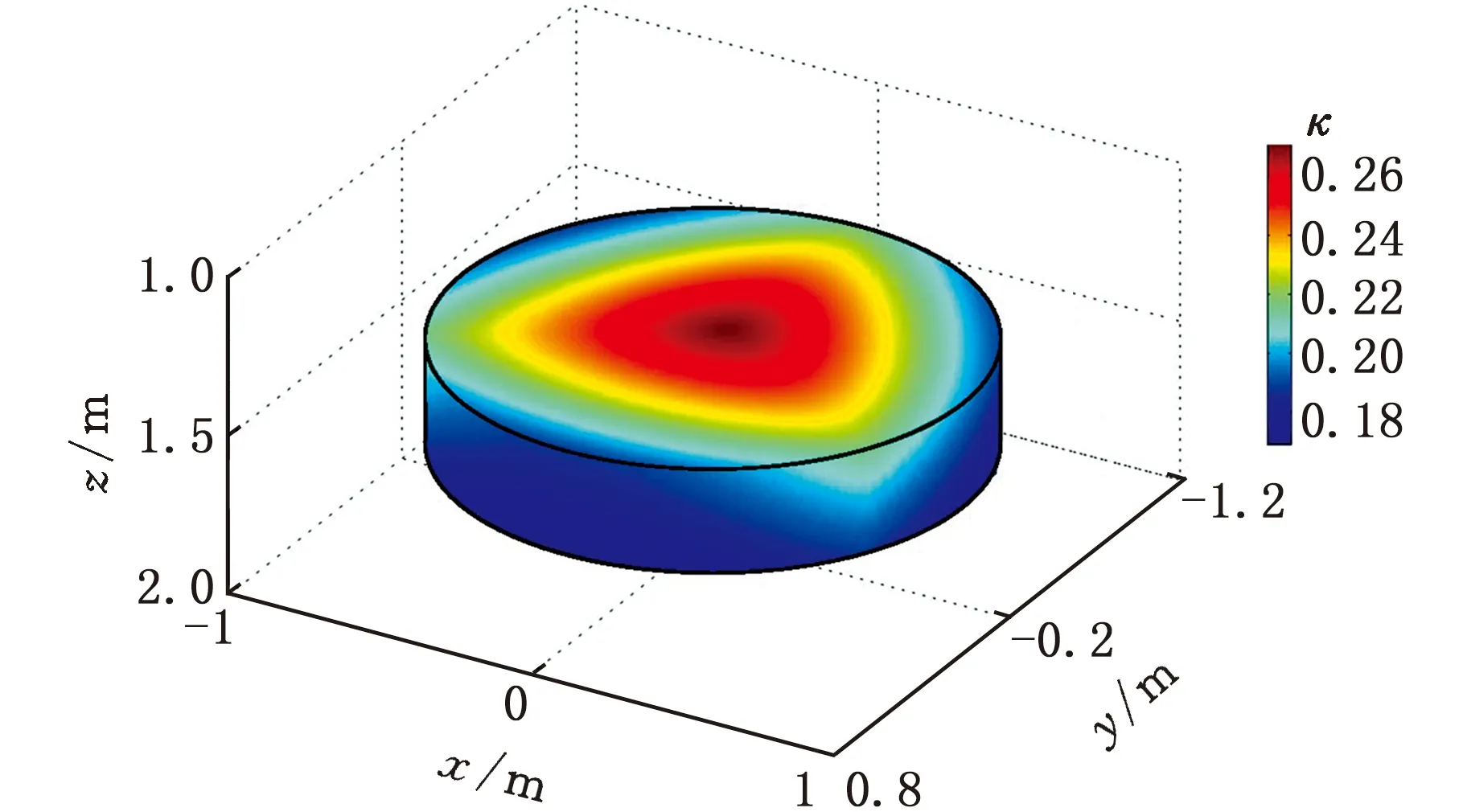
(a)R(2-RPR&RP)&UPS

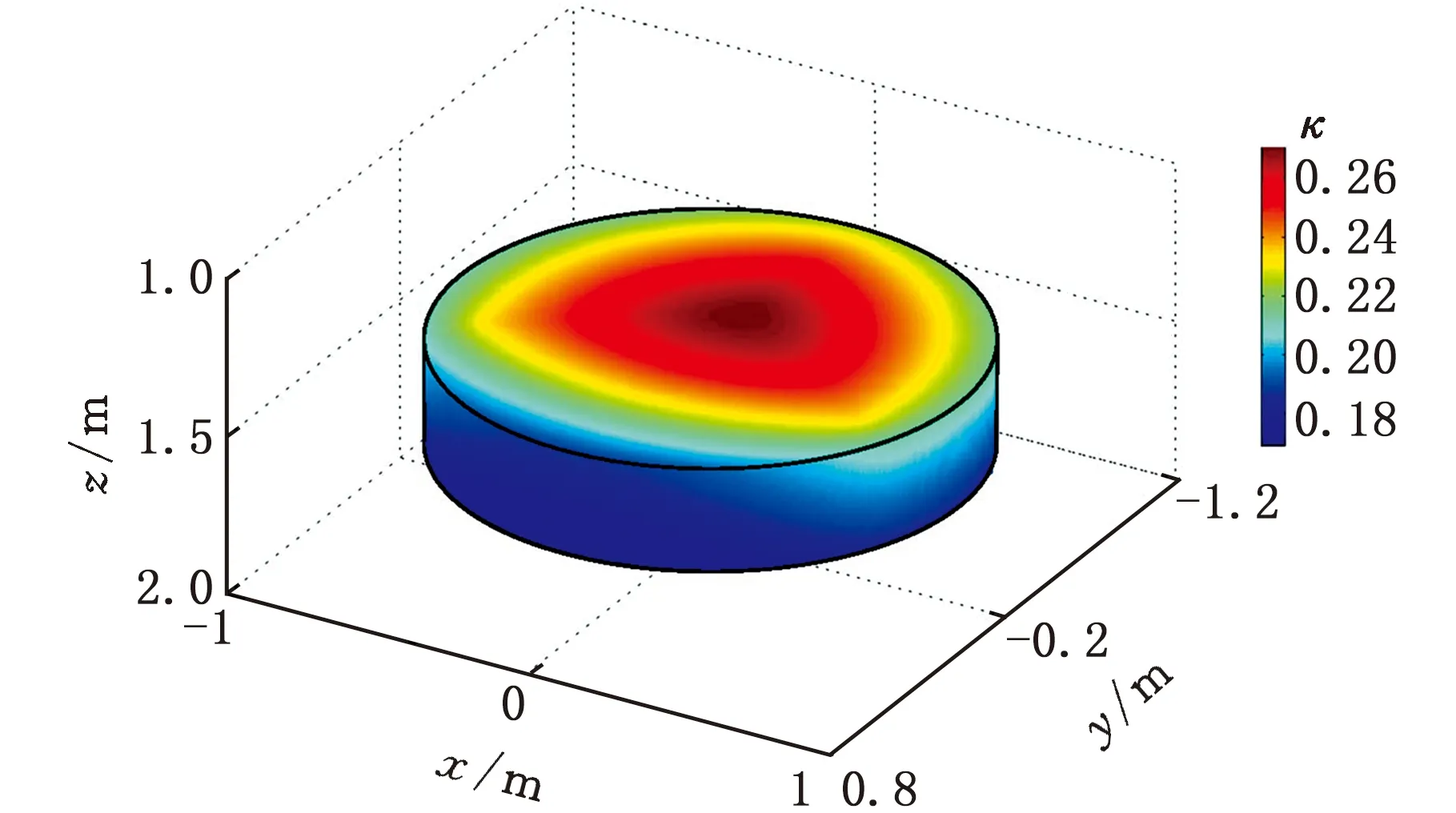
(b)R(2-RPR)&SPR图8 R(2-RPR&RP)&UPS与R(2-RPR)&SPR并联机构的运动/力传递特性分布规律Fig.8 Motion/force transmissibility distributions of theR(2-RPR&RP)&UPS and R(2-RPR)&SPRparallel mechanism

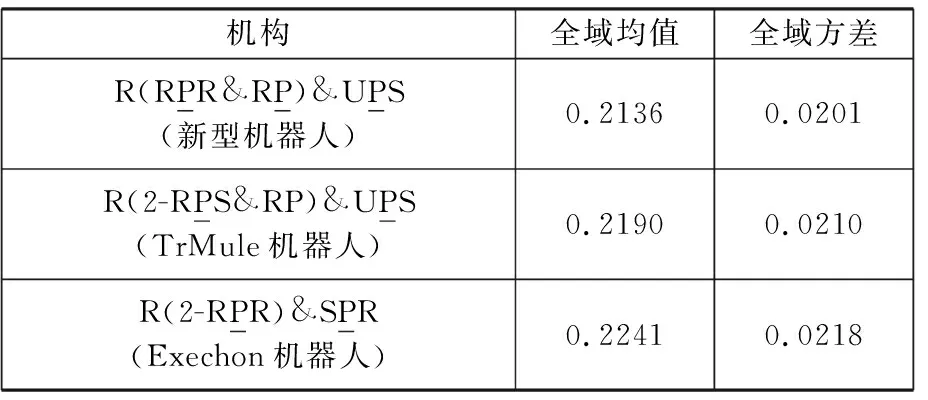
表3 全域运动/力传递特性对比

考虑到上述对比分析局限于给定的任务空间WT，故图9进一步示出了三种并联机构在可达工作空间中x-z和y-z坐标平面上的运动/力传递特性分布规律。由图可见，三种机构的可达工作空间接近，且力/运动传递特性基本相当。上述对比分析结果有效验证了本文所提出尺度综合方法的有效性，同时为该新型混联机器人的应用提供了理论依据。

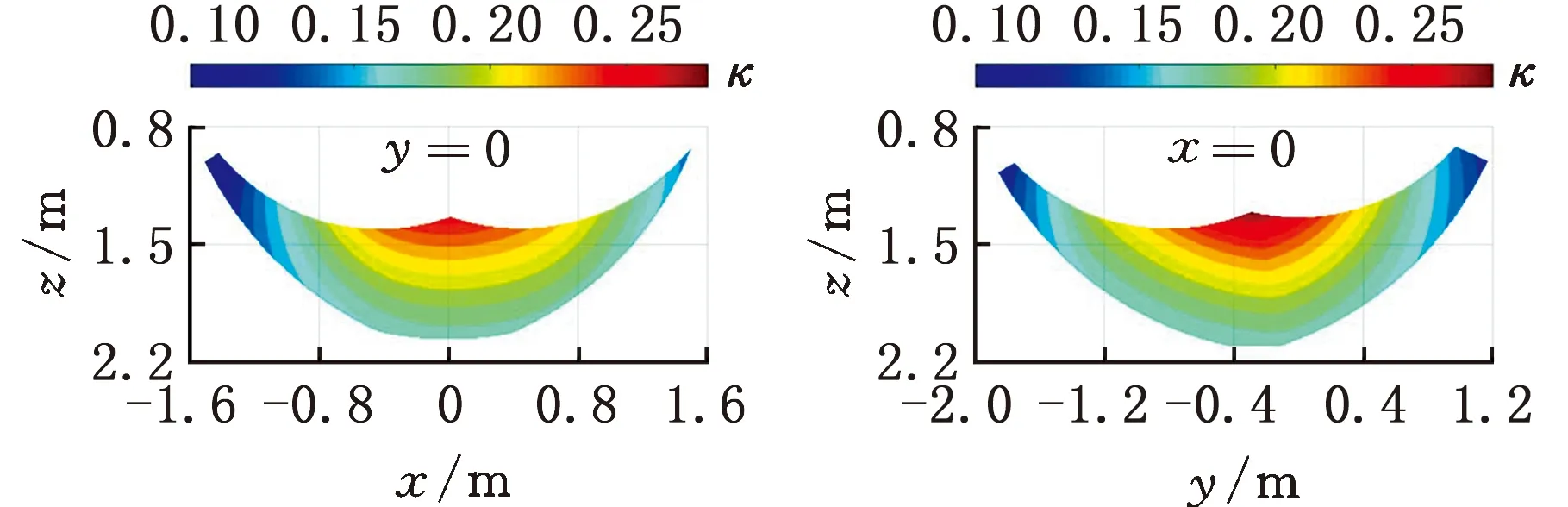
(a)新型机器人：R(RPR&RP)&UPS

(b)TriMule机器人：R(2-RPR&RP)&UPS

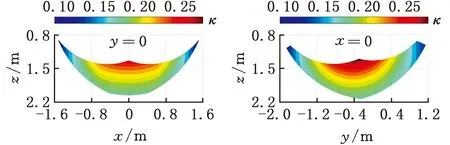
(c)Exechon机器人：R(2-RPR)&SPR图9 三种并联机构在可达工作空间中的运动/力传递特性对比Fig.9 Comparison of the motion/force transmissibilityof three parallel mechanisms in the reachable workspace

5 结论

(1)提出了一种新型非对称五自由度混联机器人，其中的三自由度1T2R位置型并联机构包含一条无约束UPS主动支链，和一个由一条RPR支链、一条RP支链组成的1T1R平面并联机构，且该平面并联机构的连架杆件通过一对连架R副与机架连接。这一特殊构型使得该机器人有机融合了Exechon和TriMule机器人的优点。