海洋平台分布式动力吸振

王 禹， 缪旭弘， 王 娜， 李海超， 庞福振,

(1.中国船舶及海洋工程设计研究院， 上海 200011； 2.哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001；3.中国人民解放军92578部队， 北京 100161； 4.哈尔滨工程大学 烟台研究院， 山东 烟台 264000)

0 引 言

海洋平台结构尺度大、激励载荷复杂，由此带来的振动问题较为明显。国际标准化组织(ISO)及各大船级社对海洋平台各区域的振动水平提出明确的限值要求[1]，与其他区域相比，对上层建筑区域内的振动水平要求更严格。在海洋平台设计初期，可通过仿真计算等方法预估振动水平可能超标的区域，并对局部结构进行优化设计[2]，但对于试航阶段的海洋平台，一旦发现振动水平超标问题，采用结构优化[3-4]等方法进行振动控制对原有平台结构改动较大、成本较高，且不易实现。考虑到上述问题，拟采用动力吸振器降低试航阶段海洋平台上层建筑低频振动。动力吸振具有结构简单可靠、对原有结构改装小、成本低等优点[5-6]，广泛应用于海洋工程领域。杨志荣等[7]将动力吸振技术应用于船舶轴系，解决其纵向振动问题，给出动力吸振器特性参数(质量比、频率比、阻尼比)与减振效果之间的关系。金咸定等[8]概述舰船尾部振动特点，用实例证明动力吸振技术在舰船尾部减振降噪方面具有一定的应用前景。郑涛等[9]通过有限元方法，利用动力吸振方法解决浮筏隔振装置在低频范围内减振效果较差的问题。然而对分布式动力吸振的研究并不多见。

为此建立四自由度主从耦合动力吸振系统的数学模型及其动力学方程，探究动力吸振器布放位置对吸振性能的影响规律；在此基础上，以板架结构为例，进一步分析动力吸振器在不同布放方案下的减振效果差异；最终结合实际问题，提出海洋平台分布式动力吸振设计，并通过有限元仿真，验证分布式动力吸振的有效性。

1 分布式动力吸振原理

动力吸振器是一种通过弹性元件把辅助质量连接到主系统(被减振结构)上的减振装置，其本质是子振动系统。分布式动力吸振器在传统动力吸振器的基础上，将单个动力吸振器分解为多个动力吸振器，并保持子振动系统的总质量不变，具有布放灵活、占用空间小、减振效果佳等优势。本节建立四自由度主从耦合动力吸振模型，探究分布式吸振器布放位置对吸振性能的影响规律。

1.1 主从耦合动力吸振模型

在工程中，实际问题往往是多自由度或无限自由度问题，为方便计算又不失一般性，建立四自由度振动系统，从理论角度展开研究。主从耦合动力吸振模型如图1所示。该模型由主结构和2个动力吸振器组成，其中主结构质量块长度为2a、质量为m1，弹簧关于质量块形心对称放置，与形心间的距离为L，刚度分别为k′1、k′2，阻尼器与弹簧位置相同，阻尼大小分别为c′1、c′2。在主结构上耦合2个动力吸振器：一个布置在形心处，质量为m2，刚度为k2，阻尼大小为c2；另一个布置在形心右侧，与形心距离为d，质量为m3，刚度为k3，阻尼大小为c3。周期性激振力作用于形心左侧，与形心距离为b，激振力大小F=F0eiω t，其中，F0为激振力幅值，ω为激振力的圆频率，t为时间。

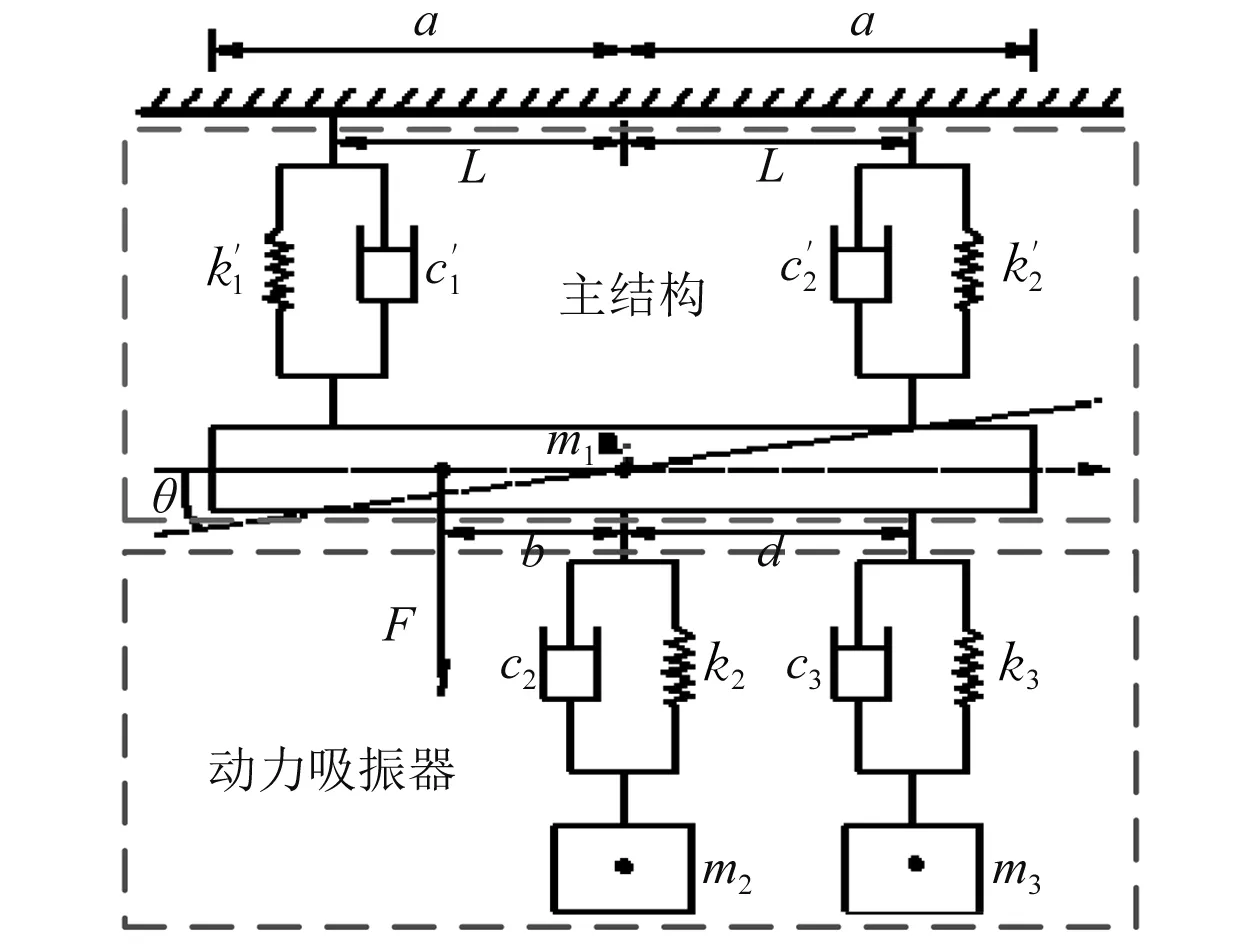
注：θ为主结构质量块绕重心旋转的角度图1 主从耦合动力吸振模型

1.2 主结构振动响应求解

求解过程较为简单，仅给出求解流程和重要步骤。

先列出主结构平动、转动和2个动力吸振器的运动微分方程。

主结构垂向平动微分方程为

(1)

式中：x1为主结构质量块重心在竖直方向上的位移；x2和x3分别为2个动力吸振器质量块在竖直方向上的位移；θ为主结构质量块绕重心旋转的角度。

主结构转动微分方程为

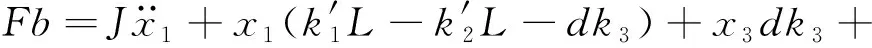
(2)

式中：J为主结构的转动惯量。

(3)

动力吸振器的运动微分方程为

(4)

(5)

联立式(1)～式(5)并整理为

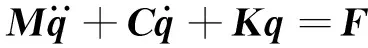
(6)

式中：M为质量矩阵；q为广义坐标列向量；C为阻尼矩阵；K为刚度矩阵；F为载荷列向量。

再定义无量纲常数，包括：动力吸振器的质量比μ(动力吸振器质量与主结构质量之比) 、频率比υ(动力吸振器固有频率与主结构固有频率之比)、阻尼比ζ(动力吸振器阻尼与其临界阻尼之比)、外激励频率与主结构频率比η。

在此基础上，利用MATLAB软件，可得到主结构垂向平动动力放大系数β1和转动动力放大系数β2为

(7)

(8)

式(7)和式(8)中：X1为主结构垂向平动幅值；δ1为主结构在F0作用下的质心垂向位移；θ0为主结构转动幅值；δ2为主结构在F0作用下的转角；t1、t2和N为关于μ、ζ、υ、η的代数式。

1.3 布放位置对吸振性能的影响

已有文献[10-15]指出：(1) 动力吸振器质量比越大，吸振性能越好，但应综合考虑吸振器其他方面的影响；(2) 动力吸振器阻尼比越小，在共振频率下的减振效果越好，反之可拓宽吸振器工作频带；(3) 当动力吸振器的固有频率与激励力频率相同时，吸振效果最佳。

从理论角度对动力吸振器布放位置开展的研究较少，为此，基于所得主结构的振动响应，探究布放位置对主结构减振效果的影响规律。动力放大系数β1和β2是关于无量纲参数μ、υ、ζ、η和d′(d′=d/L)的函数。分别令μ=0.05、υ=1.00、ζ=0.15，则可绘制d′=0.2、d′=0.5和d′=0.8时主结构的幅频响应曲线，如图2所示。

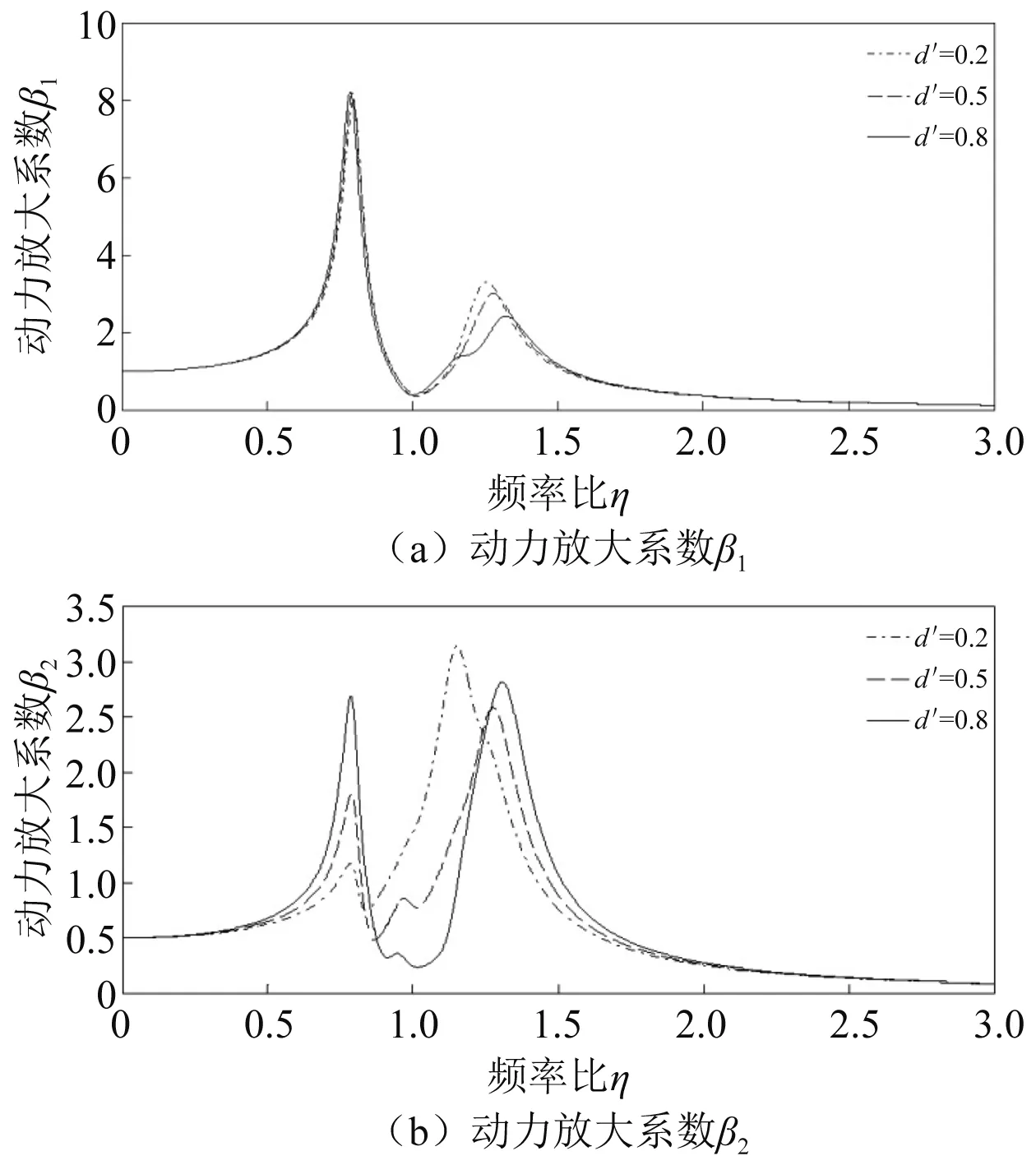
图2 布放位置对动力放大系数的影响

在其他条件不变的情况下，由图2可知：对于β1而言，将动力吸振器布放在不同位置对其几乎没有影响；对β2而言，动力吸振器布放位置距主结构形心越远，减振效果越好。发生这种现象的原因如下：在主结构垂向平动时，各个位置的振动响应相同，因此布放位置对减振效果影响不大；在转动时，远离形心位置的振动更显著，将动力吸振器布放在振动响应大的位置能更好地降低结构振动响应。

此外，可根据该方法探究μ、υ、ζ对吸振效果的影响规律，所得规律与文献一致。

2 海洋平台板架结构分布式动力吸振

由第1.3节可知：动力吸振器应布置在振动响应大的位置。在海洋平台板架结构中，振动响应最大的位置为固有振型下的波腹位置，二阶以上的振型中均存在多个波腹，此时可采用分布式动力吸振对各个波腹进行同时控制，但仍需进一步探究动力吸振器数量和布放方案对减振效果的影响。

2.1 板架结构模型

根据海洋平台图纸，建立与上层建筑区域甲板具有相同尺寸的板架结构，板架尺寸为13.5 m×5.0 m，厚度为16 mm，如图3所示，板架结构总质量为12 404 kg。四周边界条件为简支，可计算得到该板架的一阶模态固有频率(f=16.6 Hz)和二阶模态固有频率(f=21.0 Hz)，如图4所示。

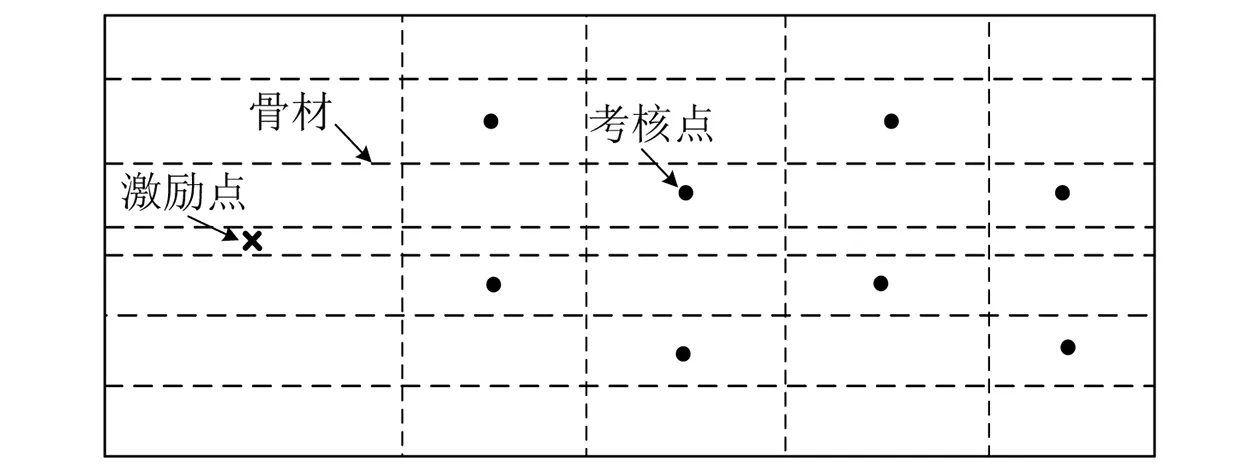
图3 板架结构模型示例

图4 板架结构模态

2.2 板架结构分布式动力吸振

为探究动力吸振器数量对吸振性能的影响规律，开展针对板架结构二阶模态的分布式动力吸振研究。图3中已注明激励点和考核点位置，在激励点加载单位力，以8个考核点的平均振动加速度级为考核指标，对板的振动响应情况进行考核。动力吸振分布方案如图5所示。

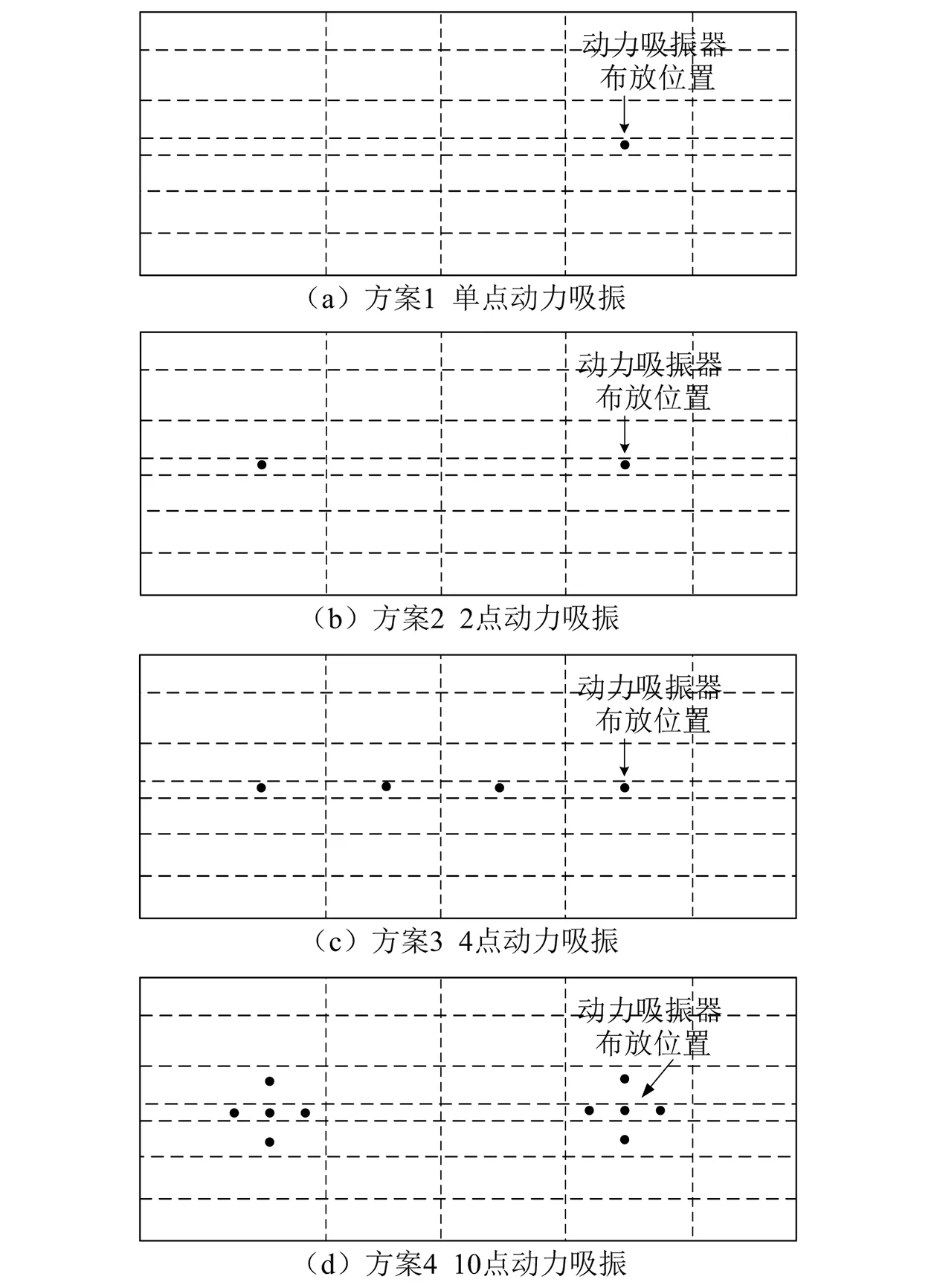
图5 动力吸振器布置工况

在各工况下，动力吸振器总质量均为板架结构质量的5%，动力吸振器自身固有频率为21.0 Hz，阻尼比为0.15。计算结果如图6所示。

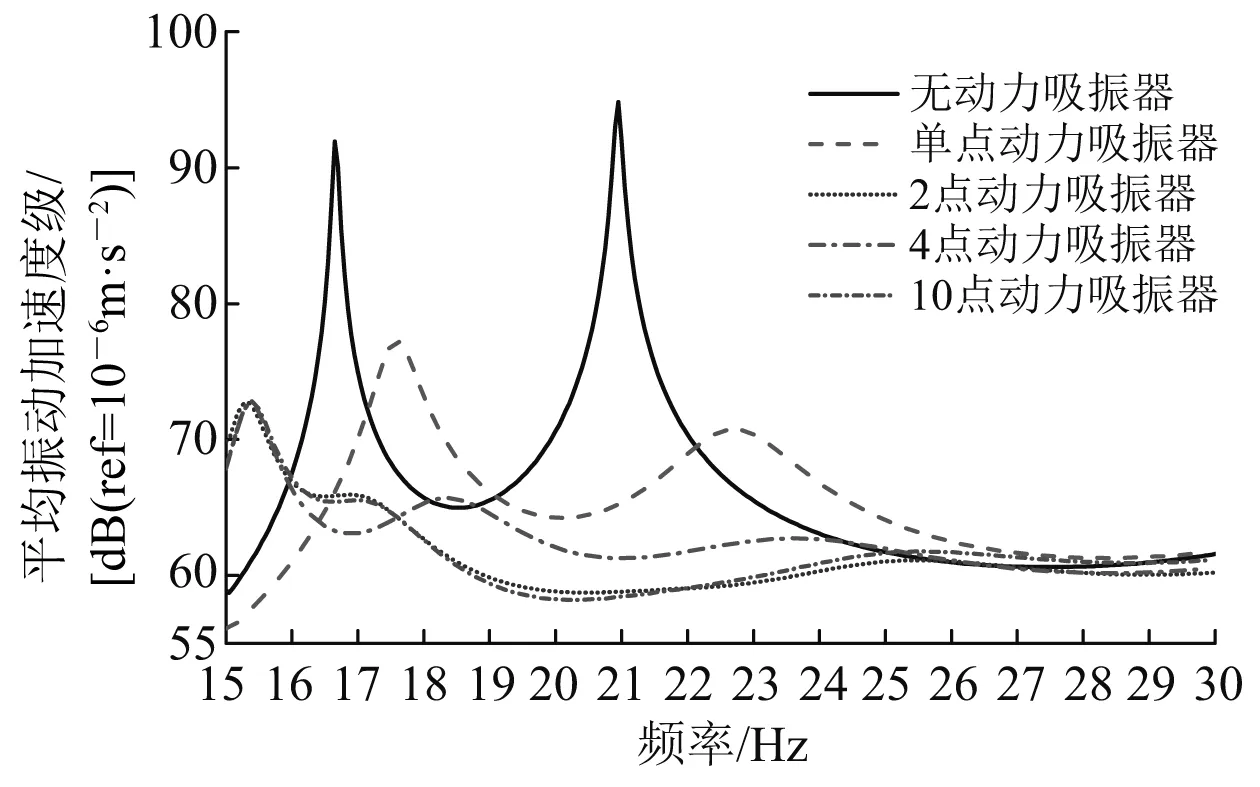
图6 考核点平均振动加速度级

对比分析f=21.0 Hz时各工况板架的平均振动加速度级，得到如下结论：(1) 将单个动力吸振器分解成2个并布放在波腹处，可增加6.4 dB的减振量；(2) 将波腹处动力吸振器分解成多个后放在原位置附近，减振效果几乎不变；(3) 将波腹处动力吸振器分解成多个后布置在其他位置，减振效果减小2.5 dB。因此，在利用分布式动力吸振技术对板架结构某一特征频率进行振动控制时，应将动力吸振器分布在振型的每个峰值处。

3 海洋平台上层建筑分布式动力吸振

针对海洋平台螺旋桨激励引起的上层建筑低频振动问题，开展分布式动力吸振研究。

3.1 海洋平台模型建立

依据某海洋平台图纸，绘制海洋平台简图(见图7)，建立1∶1海洋平台有限元仿真模型(见图8)。在空载情况下，海洋平台总质量约1 987.7 t，其中生活区甲板质量为12 404 kg。平台部分结构处于水下，需考虑流固耦合效应，因此建立流场结构模型，施加无反射边界条件对模型进行截断。最终得到有限元整体模型，如图9所示。

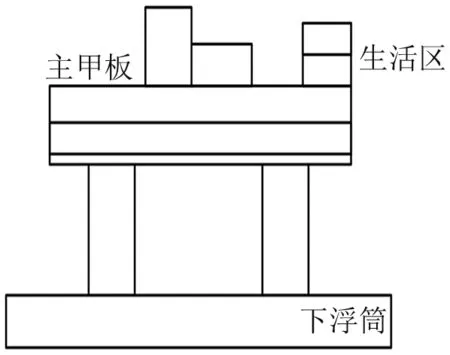
图7 海洋平台简图

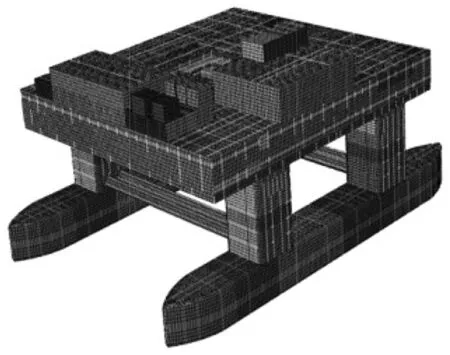
图8 海洋平台有限元模型

图9 有限元整体模型

3.2 海洋平台振动特性

对海洋平台生活区局部模态进行分析，得到平台生活区模态振型，如图10所示。

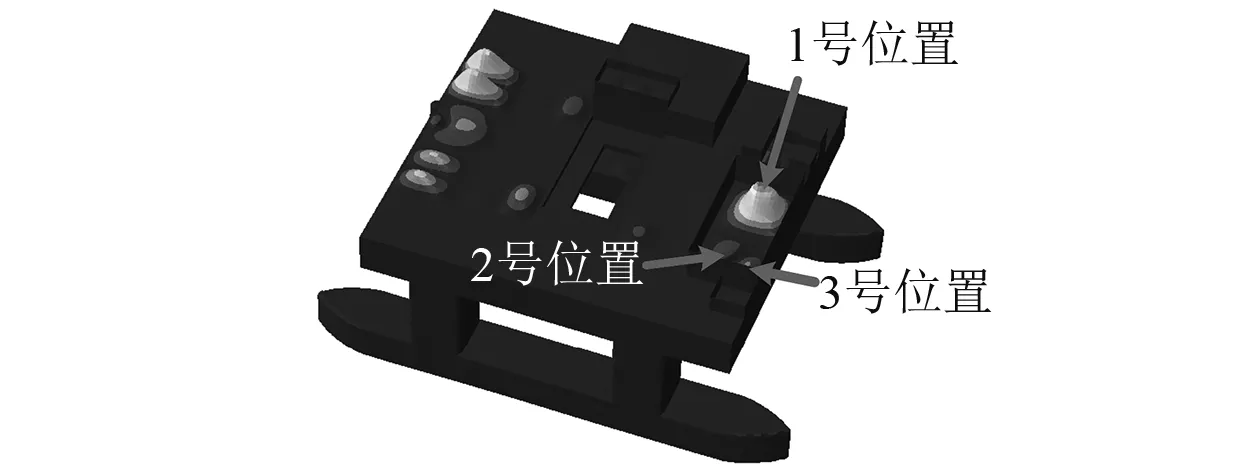
图10 生活区局部模态(f=20.6 Hz)

由局部模态计算结果可知，在该海洋平台上层建筑区域内共存在3个波腹，其中1号位置波腹的幅值明显大于2号和3号位置的幅值，说明1号位置的振动响应对区域内平均振动有较大贡献量。

在完成振动模态分析后，在对应位置施加实船测试载荷。计算海洋平台上层建筑区域在低频范围内的振动响应，在上层建筑矩形区域内按照5×3矩阵形式均匀分布15个考核点，将考核点的振动加速度响应进行能量平均，能量平均公式为

(9)

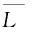
实船测试载荷及生活区平均振动响应如图11所示。

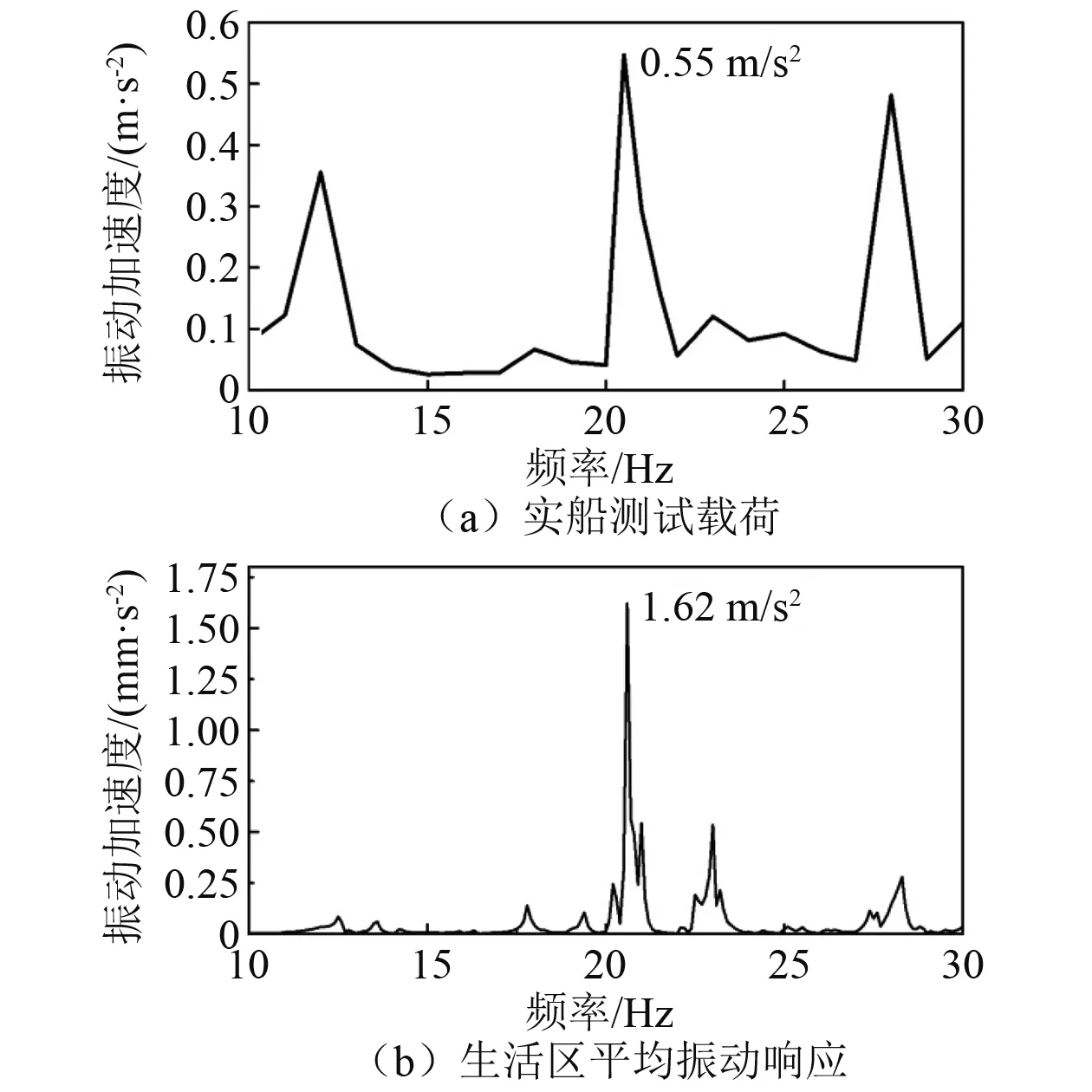
图11 实船测试载荷及生活区平均振动响应

由图11可知，生活区平均振动响应在20.6 Hz存在明显峰值，并且与激励力峰值频率和局部模态固有频率均相同。振动响应峰值是由生活区局部与实船载荷形成共振引起的，为此采用分布式动力吸振方法对生活区进行振动响应控制。

3.3 海洋平台上层建筑动力吸振方案

根据动力吸振器参数及位置对减振效果的影响规律，拟定方案(见表1)，其中动力吸振器总质量均为生活区甲板总质量的2%(即248.0 kg)，考虑到1号位置振幅明显大于2号和3号位置，方案2和方案3将更多的质量分配在1号位置。

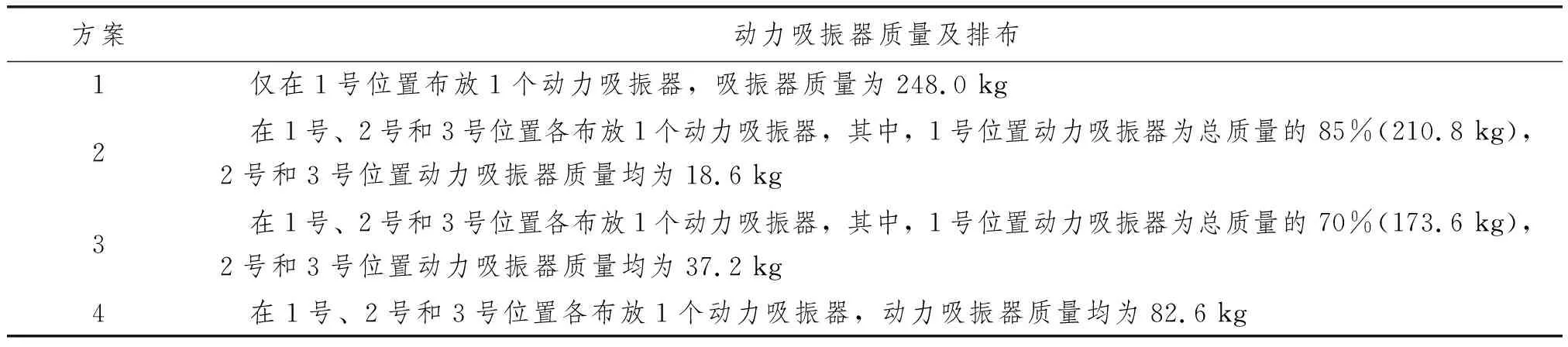
表1 海洋平台上层建筑动力吸振方案

通过计算得到生活区平均振动加速度响应曲线如图12所示，各方案响应曲线趋势基本保持一致，但在20.6 Hz附近的峰值有一定差异。表2为动力吸振器减振效果。由表2可知：方案1仅对1号位置的波腹进行控制，具有良好的减振效果(7.3 dB)；方案3和方案4采用分布式动力吸振对多个波腹进行振动响应控制，但1号位置动力吸振器的质量均小于方案1，对1号位置振动响应控制不足。因此，方案3和方案4的减振效果不如方案1。方案2则在针对1号位置进行振动的同时，又对2号和3号位置进行适当控制，其减振效果(11.0 dB)最佳。

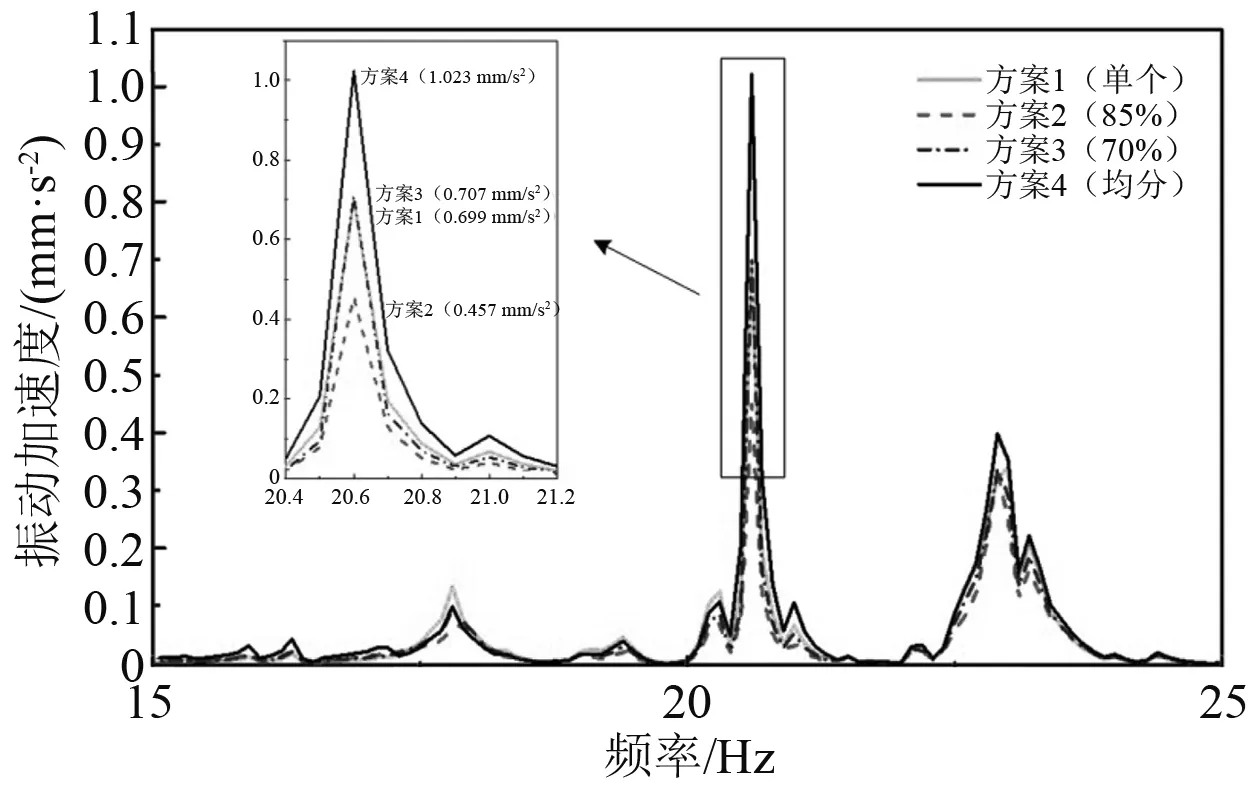
图12 生活区平均振动加速度响应(控制后)

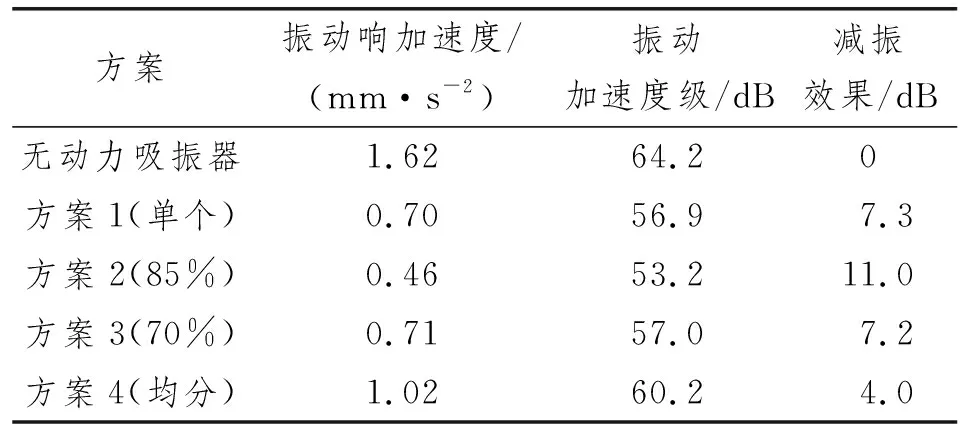
表2 动力吸振器减振效果

综上所述：单个动力吸振器可明显降低生活区振动响应；采用分布式动力吸振，在动力吸振器总质量不变的情况下，减振效果可达11.0 dB，与单个动力吸振器相比，减振效果提高3.7 dB。

4 结 论

从理论上探究动力吸振器布放位置对减振效果的影响规律，以海洋平台板架结构为例，进一步探究动力吸振器数量和布放方案对减振效果的影响，并将所得规律应用于海洋平台，对海洋平台上层建筑振动响应进行控制，主要结论如下：

(1) 海洋平台上层建筑区域在应用分布式动力吸振后振动响应降低11.0 dB，与单点动力吸振器相比，减振效果提高3.7 dB。

(2) 动力吸振器布放在波腹位置处具有最佳的吸振效果。

(3) 保持动力吸振器总质量不变，将单个动力吸振器分解成多个，并布放在原位置附近，吸振效果几乎不变。