专家PID与SQP算法在动力定位船模试验中的应用

2021-10-28骆寒冰李元芳盛世民

中国海洋平台 2021年5期

骆寒冰，李元芳，谢芃，盛世民

(天津大学船舶与海洋工程系，天津 300350)

0 引言

在海洋石油工程施工作业时，采用动力定位施工船舶相对于普通锚泊船舶具有效率高的优势，尤其在深水作业中，动力定位施工船舶的应用越来越多。动力定位系统主要包括控制算法和推力分配算法。常用的控制算法主要有比例-积分-微分(Proportional Integral Differential，PID)算法[1-2]和最优控制与Kalman滤波理论相结合的线性二次型高斯(Linear-Quadratic-Gaussian，LQG)算法[3]等，其中PID算法的控制原理简单、控制效果良好，在工程控制领域应用范围较广。随着对控制算法研究的深入，智能控制开始应用于船舶动力定位控制，如神经网络控制[4]、模糊控制[5]和非线性模型预测控制[6]等算法。在推力分配算法上，LIANG等[7]提出序列二次规划(Sequential Quadratic Programming，SQP)算法，该算法可实现对推力大小和方向的有效控制。也有学者将遗传算法[8]、人工蜂群算法[9]等应用于推力分配算法中。

本文提出专家PID控制算法，结合SQP算法，基于LabView软件和NI硬件，开发动力定位模型试验控制系统，针对某海洋工程施工船舶，在天津大学港口工程试验水池进行动力定位模型试验。

1 动力定位控制系统控制理论

动力定位模型试验控制系统主要由控制算法和推力分配算法构成。其中，控制算法由滤波算法和控制器两大部分构成：通过滤波算法对船舶运动数据进行滤波处理，滤除船舶波频运动和噪声，得到船舶状态(船舶的位置和艏向角)的估计值，以去除船舶的高频运动，使控制器只针对船舶运动的低频部分进行控制，减少动力定位的能耗和机械损耗；控制器根据输入的估计值和定位设置的目标值通过控制算法得到使船舶恢复目标状态所需要的在纵荡、横荡和艏摇三自由度方向的力和力矩的大小，并根据推力分配算法得到各推进器的转速、螺距、转向角等控制指令。

1.1 滤波算法

滤波算法选择低通滤波+陷通滤波的方式。

低通滤波的传递函数为

(1)

式中：h(s)为在拉普拉斯复频域上表示的传递函数；ωn为低通滤波截止频率；s为拉普拉斯复频率。

陷通滤波的传递函数为

(2)

式中：ξ为陷通滤波常数。

3、农业机械运行噪声较大，教师的培训环境不理想。农业机具使用的动力装置基本是柴油机，柴油机运行时，噪声较大，产生尾气，如果在室内不通风的密闭环境下，尾气聚集对人体伤害较大。

1.2 控制算法

离散的位置式PID控制算法的基本公式为

(3)

式中：k为采样序号；U(k)为第k个采样时刻控制器产生的控制力，即纵向、横向和回转方向的力和力矩；Kp、Ki、Kd分别为控制器的比例、积分、微分系数；e(j)为第j个采样时刻输入的偏差值，为设定的目标位置与实际位置的差值。

为达到更好的控制效果，根据不同的偏差大小和变化趋势设定多组PID控制参数，即Kp、Ki和Kd。分组和参数设置的基本依据如下：

(1) 当船舶偏离目标位置时，参数设置可相对较大，此时推进器提供较大的恢复力以阻止船舶继续偏离目标位置，且偏差越大，参数设置越大。

(2) 当船舶靠近目标位置时，参数设置可相对较小，此时推进器提供较小的反力，使船舶可克服外力作用继续靠近目标位置且控制船舶速度，减少超调。

(3) 结合偏差大小和动力定位允许的精度误差进行分组，在精度误差内根据不同偏差大小设置的不同组的参数设置变化幅度较小，避免得到的力或力矩变化幅度较大，从而造成推进器磨损。

在实际控制过程中对纵荡、横荡和艏摇方向进行PID控制解耦，不考虑三者之间的耦合作用。

1.3 推力分配算法

对于普通的约束非线性规划问题：

minf(x)
s.t.hj(x)=0,j=1,2,…,l
gi(x)≥0,i=1,2,…,m
x∈Rn

(4)

运用序列二次规划法时，在xk点处的二次规划一般采用的形式为

(5)

式中：Hk为一个n阶实对称阵，有不同的定义方法，在本试验中，Hk=∇2f(xk)，即f(x)在xk点处的海赛阵；d=x-xk，即为xk点处的搜索方向，下一个迭代点xk+1=xk+αdk，在本试验中，α为一维列向量，一般向量的元素取值为1，即xk+1=xk+dk。重复上述过程，直至得到近似约束最优点x*。

推力分配对应的非线性规划问题为

(6)

式中：F1、…、F7为7个推进器提供的推力；θ1、…、θ7为7个推进器对应的方向角；lnx和lny分别为第n个推进器x和y的坐标，Fx、Fy、MN分别为控制器计算得到的纵荡、横荡力和艏摇方向力矩。

选SQP算法作为推力分配算法，可得到7个推进器的推力与方向角。在试验中，对于推力禁区引起的推力衰减，考虑船模横向2个相邻推进器之间的相互影响，认为纵向相邻推进器之间距离足够远，忽略其相互影响。当SQP算法得到的下游推进器处于上游推进器尾流中时，下游推进器的方向角调整至与计算结果较接近的禁区边缘。出于安全考虑，设置推进器方向角调整速度限制。

2 模型试验

2.1 模型设计

模型设计满足几何相似、运动相似以及弗劳德数Fr和斯特劳哈尔数Sr分别相似。缩尺比λ=1∶38。船模用玻璃钢制作，加工后船模型线与实船几何相似，船模上7个全回转推进器及其安装位置满足几何相似。主要参数如表1所示。

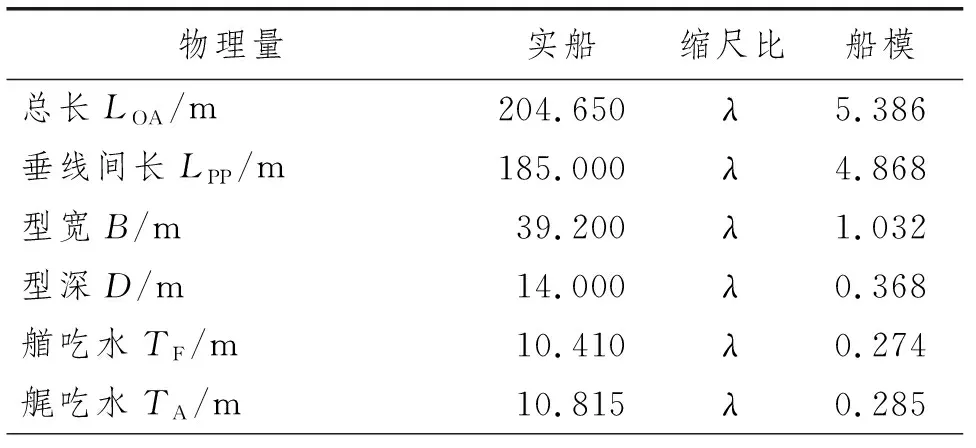
表1 实船与船模的主要参数

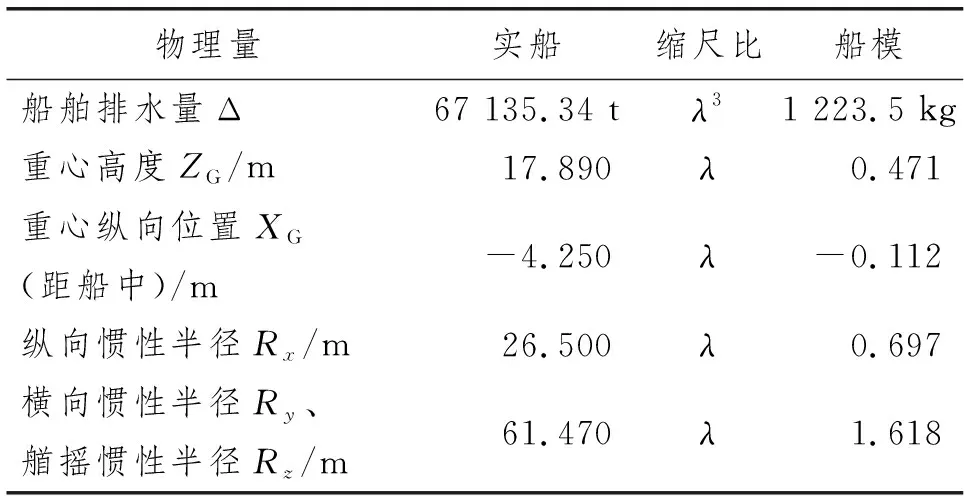
续表1 实船与船模的主要参数

船模推进器的布置如图1所示，图中①～⑦为推进器编号，7个推进器均为全回转推进器，其中①号和②号为主推进器。

图1 试验船模推进器布置示例

2.2 试验场地及测量控制系统

在天津大学港口工程试验水池进行，水池长为55 m、宽为40 m、深为1.8 m，试验水深为1.5 m，水池上有测量桥。不规则波的模拟采用JONSWAP谱进行模拟，谱峰系数取3.3。水池有风阵，可用于造定常风。图2为试验现场。

图2 试验现场

船舶动力定位系统主要包括测量系统、控制系统、推进系统。

测量系统由采集船舶六自由度运动并将数据实时传递给控制系统的非接触式运动测量系统、采集波浪波高的浪高仪和测量风速的风速仪构成。控制系统采用低通滤波+陷通滤波、专家PID控制算法和SQP算法，由LabView编程实现。

推进系统由7个全回转推进器构成，每个推进器都由2个交流伺服电机驱动，分别实现驱动推进器转动发出推力和推进器回转改变推力方向两个功能。采用美国NI(National Instrument)公司的产品CompactRIO(C-RIO)[13]控制推进器电机的转动。C-RIO系统由一个包含处理器和现场可编程逻辑门阵列(Field Programmable Gate Array, FPGA)的控制器以及信号调节I/O模块组成，在本试验中通过C-RIO编制程序，对控制系统传输的转速和方向角指令进行解析，结合通用模拟输入模块接收的推进器当前的实际方向角，将解析后的指令发送给伺服电机，伺服电机驱动控制电机转动达到调整推进器转速和方向角的目的，同时将实际方向角反馈回控制系统辅助进行下一次的控制。

3 典型试验工况结果分析

选择斜浪为150°、有义波高为1.5 m、谱峰周期为7 s、风速为8.5 m/s的典型工况，纵荡、横荡和艏摇方向的运动以及重心水平运动轨迹如图3所示，各推进器的推力与方向角如图4所示。图3和图4中所有结果已换算成实船尺度。

注：图中纵荡运动正方向指向船首，横荡运动正方向指向左舷，艏摇运动正方向为逆时针图3 船舶水平面运动情况

注：推进器方向角为0°时力的方向指向x轴正方向，逆时针方向为正，变化范围为-180°～180°图4 推进器推力与方向角

由图3可知，在该工况下船舶的纵荡、横荡和艏摇运动都较为平稳，艏摇运动呈现较为明显的周期性，船舶的水平运动轨迹集中在原点附近。对船舶重心水平运动轨迹进行分析，船舶总长为204.65 m，重心水平运动轨迹全部在1.0 m圈内，即船舶运动均在船长的0.5%范围内；超过90%(94.44%)的点在0.6 m圈内，即船长的0.3%。艏摇角度最大不超过0.5°。因此，在该海况下所开发的动力定位系统控制的整体定位效果较好。DNV规范[14]以船能保持在水平半径3 m的范围内，艏摇角度保持在±3°的范围内作为动力定位可保持位置的接收标准。以此为标准，船舶动力定位位置是可接收的。

由图4可知，各推进器推力分配较为均衡，①号与②号、③号与④号、⑤号与⑥号推进器的分配结果接近。各推进器推力均在同一个数量级，单个推进器的推力存在锯齿形波动，这可能是由专家PID控制分组设置参数时参数变化幅度较大引起的。推进器推力均值较小，实船①号、②号推进器最大推力为680 kN，③号、④号、⑤号、⑥号、⑦号推进器最大推力为540 kN，推进器实际推力不超过最大推力的10%，最大波动约为最大推力的5%，对推进器磨损产生的影响也相对较小；推进器的方向角较为稳定，最大标准差约15°，③号、④号、⑤号、⑥号、⑦号推进器方向角的标准差不超过10°，方向角旋转角度范围较小，电机运行稳定，推进器磨损较小。

综合上述定位效果和推进器推力分配的结果，认为设计的控制系统定位效果良好，可用于水池船模试验。