基于分层数据筛选的跨项目缺陷预测方法

赵 宇，祝 义，2，于 巧，陈小颖

1.江苏师范大学 计算机科学与技术学院，江苏 徐州 221116

2.南京航空航天大学 计算机科学与技术学院，南京 210016

软件缺陷预测是当前软件测试和机器学习紧密结合的一个研究热点，目的是期望在项目开发的早期阶段预测出某些模块中是否含有缺陷，从而合理地分配测试资源，最大化资源利用率。目前大部分的学术研究都关注项目内缺陷预测（Within Project Defect Prediction，WPDP）[1]，也就是选择同一项目的部分数据集作为训练数据，剩下的部分作为测试数据来构建模型。但是一方面这种模型的普适性太差，不能用于预测其他项目；另一方面就是实际开发中的项目可能是一个新启动的软件项目，没有历史数据作为训练数据，因此无法构建缺陷预测模型。针对此实际问题有学者提出了跨项目缺陷预测（Cross Project Defect Prediction，CPDP）[2-3]，从其他项目中选择合适的数据集作为训练数据来训练缺陷预测模型，然后用于预测目标项目是否含有缺陷。Herbold[4]提出了两种基于距离相似性的源项目训练数据集选择策略。但是他们的方法与项目内缺陷预测的性能存在差距。李勇等人[5]提出了一种基于目标项目的两阶段筛选训练数据集的方法，但是训练出的模型与项目内预测相比性能提升有限。MA等人[6]从为源项目中的实例设置权重的角度出发，提出一种新颖的跨项目缺陷预测方法TNB（Transfer Naïve Bayes），该方法通过对目标项目数据的分布进行预测，来为候选源项目中的实例设置权重，但该方法仅适用于朴素贝叶斯模型。针对现有研究的不足，本文对训练数据集的选择方法进行了改进，提出了一种基于分层数据筛选的跨项目缺陷预测方法。

1 相关工作

跨项目缺陷预测是使用其他项目的数据来预测目标项目中是否存在软件缺陷，此前有大量工作证实了跨项目缺陷预测的可行性[7-8]。但是随着公共数据集数量的增加，在如此庞大的数据存储库中找到与目标项目中的实例相似的训练数据变得十分困难，因此有研究人员从训练数据集简化的角度来选择与目标项目最相似的源项目和最相似的实例。Zimmermann等人[8]从项目的上下文因素来计算项目的相似性，将622对跨项目预测结果与项目之间的相似性相关联，构建出决策树为候选源项目集的选择提供了参考。He等人[9]探讨了源项目数据集属性的分布特征对于选择合适的训练数据集进行跨项目缺陷预测是否有价值，他们考虑了16种不同的分布特征，其中众数、中位数、均值和调和平均数等分布特征可以描述属性取值的中心度量趋势，而极差、异众比率、四分位距、标准差和变异系数可以描述属性取值的离散趋势度量，偏度和峰度可以描述属性取值的分布形态。Turhan等人[10]从实例级别为目标项目里的每个实例从源项目中挑选距离最近的k个实例。从测试集角度出发选择训练数据，使用的是k-NN算法，如果目标项目中有100个实例，则最终选出100×k个实例作为训练数据集。Peters等人[11]也是从实例级别考虑，但是他们认为训练数据集会提供比测试数据集更多的有关缺陷的信息，因此针对源项目中的每个实例，从目标项目中识别出与之距离最近的实例并进行标记，随后对于目标项目中已标记的实例，从源项目中选出与之距离最近的实例并添加到最终的训练数据集中。Nam等人[12]和Panichella等人[13]通过对源项目数据和目标项目数据同时进行min-max标准化或z-score标准化，经过标准化后的数据取值在保持原有取值分布特征不变的情况下处于同一量纲中，从而减小源项目和目标项目数据集间的分布差异。文献[14-17]也都是从度量元取值变换的角度出发，分别对源项目和目标项目的数据进行log转换、rank转换、Box-Cox转换和取值修正。通过这些方法可以使源项目数据和目标项目数据都接近于正态分布，从而提高了源项目和目标项目之间的相似度，最终达到提高缺陷预测性能的效果。He等人[18]提出了一种两阶段筛选方法，在第一阶段从粗粒度角度入手，即先选择最相似的源项目，第二阶段在细粒度角度筛选，从已经选好的源项目中选择最相似的实例集合。在第一阶段是根据项目属性的5个分布特征：最大值、最小值、中值、均值和标准差，根据欧式距离计算出最相似的k个源项目，在第二阶段从这k个源项目中采用Burak过滤法或者Peters过滤法选择出最相似的实例集合。

2 基于分层数据筛选的跨项目缺陷预测方法

本文假设源项目和目标项目特征相同，基于该假设提出一种基于分层数据筛选的跨项目缺陷预测方法。该方法采用分层筛选的策略实现了训练数据的选择，并给出了相应的算法。

2.1 方法流程

方法流程如下：（1）提取所有项目属性的分布特征；（2）选择与目标项目最相似的源项目集得到候选源项目集；（3）在候选源项目集中选择与目标项目中实例最相似的实例集合得到候选实例集；（4）使用候选实例集训练缺陷预测模型。方法框架如图1所示。

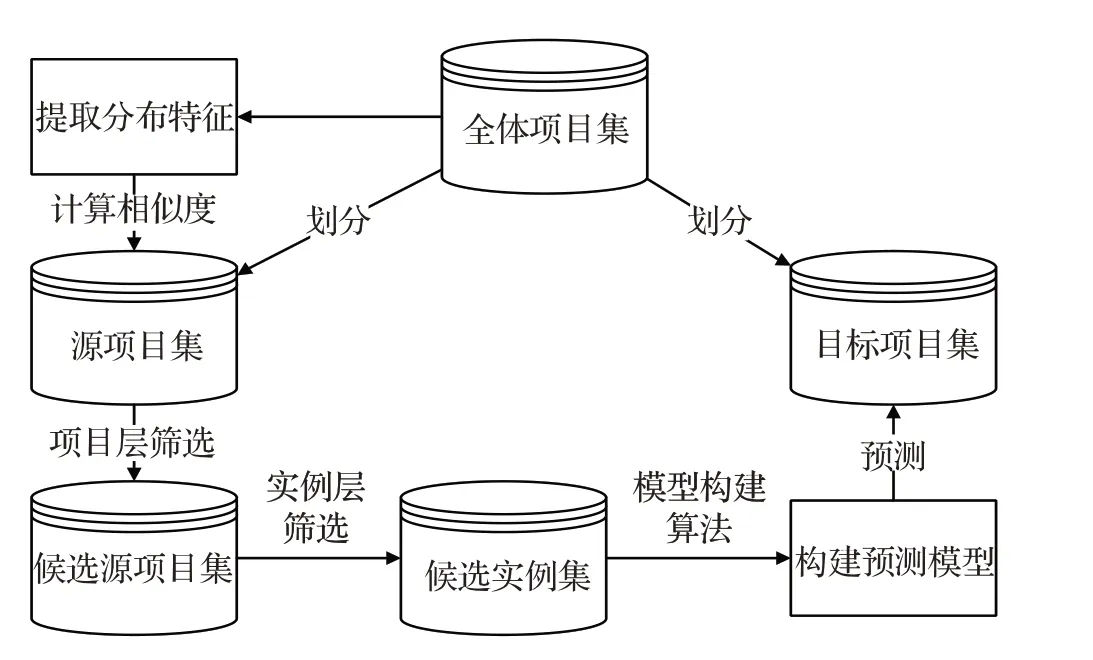
图1 方法框架Fig.1 Method framework

2.2 数据结构描述

基于分层数据筛选的跨项目缺陷预测方法的核心问题是如何选取与目标项目最相似的源项目集以及如何从选定的源项目集中选取最相似的实例集。

接下来对方法中使用的数据结构进行简要的描述，符号S表示软件项目集合，Ssource表示源项目集，Scandidate表示候选源项目集，Starget表示目标项目集，S={R1,R2,…,R w}表示一共有w个软件项目；符号I表示实例集合，Icandidate表示候选实例集，每一个软件项目Ri={I1,I2,…,I n}表示每个软件项目有n个实例，I i表示第i个实例；每一个实例I i={f i1,f i2,…,f im,y i}表示第i个实例有m个度量属性f ij(j=1,2,…,m)和一个缺陷指标yi，其中度量属性符号f ij表示一个软件项目中第i个实例的第j个度量属性，缺陷指标y i∈{Y,N}，yi=N表示该项目中第i个实例没有缺陷，yi=Y表示该项目中第i个实例有缺陷。与此同时定义一个度量属性向量Fi={f1i,f2i,…,f ni}表示一个软件项目中的所有n个实例的第i个度量属性，定义一个属性分布特征向量D j={mean(F j),median(F j),skew(F j),kurt(F j)}，该项量表示一个软件项目中所有n个实例的第j个度量属性的分布特征，同时定义一个项目分布特征向量V={D1,D2,…,D m}表示一个项目中所有n个实例的所有m个度量属性的分布特征。Vsource表示源项目集分布特征向量，Vtarget表示目标项目集分布特征向量。基于分层数据筛选的跨项目缺陷预测方法的核心目标是获取Icandidate。方法描述的结构特征如图2所示。

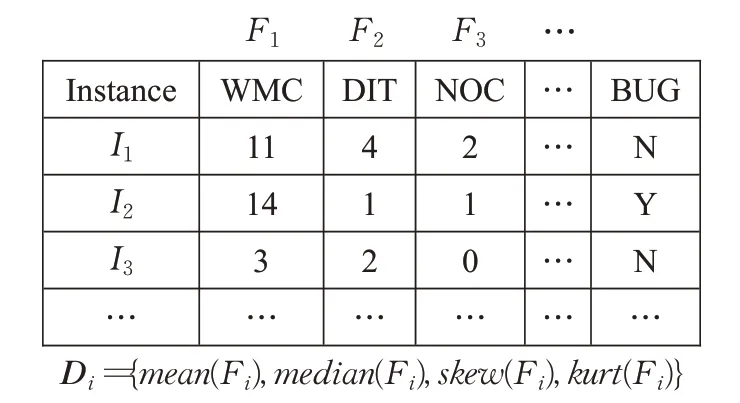
图2 方法结构Fig.2 Method structure

使用的属性的分布特征是均值（mean）、中值（median）、偏度（skew）和峰度（kurt）四个分布特征。He等人[9]的研究成果说明了项目属性的分布特征对选择相似的训练数据集是有价值的。之后Herbold等人[4]认为属性的分布特征不应选取过多，所以选取了属性的均值（mean）和标准差（std）两个分布特征使用k-NN算法进行了与目标项目相似的源项目集合的选取，但是实验结果不是很理想。本文中在选取相似的源项目之前先对所有项目的属性取值进行log变换，log变换的目的是将属性取值分布接近于正态分布。然后，选取了数据的中心趋势度量统计量-中值和均值以及数据分布形态的度量-偏度和峰度。使用欧氏距离（Euclidean Distance，ED）公式计算项目层筛选阶段中源项目与目标项目之间所有属性分布特征向量的距离来表征两项目的数据分布相似性，然后选择距离值最小的k个项目构成候选源项目集（见算法1）。

算法1

输入：初始源项目集Ssource和目标项目Starget；

1.初始化集合Scandidate、距离列表ED_List和规模参数k；

2.使用log变换对所有数据进行数据处理；

3.抽取所有项目的属性分布特征向量D j={mean(F j),median(F j),skew(F j),kurt(F j)}并合并每个项目的属性分布特征向量得到源项目集属性分布特征向量Vsource和目标项目的属性分布特征向量Vtarget；

4.计算源项目集的属性分布特征向量Vsource和目标项目的属性分布特征向量Vtarget的欧式距离，将距离值和对应的源项目名称保存在距离列表ED_List中；

5.对距离列表ED_List进行排序，选出排序后的前k个源项目作为Scandidate；

输出：候选源项目集Scandidate。

算法1的输入是源项目集和目标项目，输出是与目标项目相似的候选源项目集。第1步是初始化相关数据结构，Scandidate是最终输出集合，ED_List是存放源项目集与目标项目之间相似度的列表，k是要选择的相似候选源项目集的规模；第2步是数据预处理过程，即对源项目集和目标项目所有数据进行数据转换，这里使用的是log转换，其实还有其他常用的数据预处理方法，比如最小最大化处理和均值方差标准化等等；第3步是提取所有项目的属性分布特征向量D j={mean(F j),median(F j),skew(F j),kurt(F j)}，然后合并项目的属性分布特征向量，Vsource和Vtarget即是源项目集和目标项目的所有属性分布特征向量合并而成的项目分布特征向量；第4步是计算源项目集和目标项目的相似度，源项目集和目标项目的相似度值和对应的源项目保存在ED_List列表中；第5步是对ED_List列表中的相似度值进行升序排序，最后选出排序后的前k个源项目作为Scandidate。

在选出与目标项目相似的源项目数据集Scandidate后，要从Scandidate中的所有实例中选择出与目标项目Starget中的实例最相似的实例子集。在这方面已有的研究分成两种思路，Burak过滤法从目标项目实例的角度出发来选择训练实例，认为目标项目中的实例应该主导训练实例的选择过程。Peters过滤法则认为候选源项目数据集中的实例的内容丰富，会提供比目标项目数据集中的实例更多的关于缺陷的信息，因此该方法是为每个训练实例找到最接近的测试实例。两种思路如图3所示。图中红色圆圈是目标项目，黑色圆圈是候选训练项目。本文选用Burak过滤法的思路进行训练实例的选择，即针对目标项目中的每个实例在候选源项目数据集的实例中选出与目标项目中的每个实例相似度较高的一定数量的候选实例。

图3 过滤法比较Fig.3 Comparison of filtering methods

由于余弦距离对特征向量绝对数值不敏感，更多是从方向上区分向量间的差异。为了修正不同项目间可能存在的度量标准不统一，李勇等人[5]在筛选相似项目时使用余弦距离计算出与目标项目距离最近的源项目集合。然而在计算向量相似性的时候皮尔逊相关系数往往比余弦距离更精确[19]。余弦相似度会受到向量平移的影响，而皮尔逊相关系数具有平移不变性和尺度不变性。因此在使用Burak过滤法进行实例筛选时使用皮尔逊相关系数作为衡量实例相似性的方法，然后比较相关系数值的大小得到候选实例集（见算法2）。

算法2

输入：候选源项目集Scandidate和目标项目Starget；

1.初始化集合Icandidate和相关系数列表Pcc_List和规模参数h；

2.合并所有输入的候选源项目集得到合并后的项目集Smerge；

3.计算所有源项目集实例和目标项目中实例的相关系数；

4.将步骤3计算得到的相关系数和对应的实例编号保存在列表Pcc_List中；

5.对列表Pcc_List进行排序，选出排序后的前h个实例作为Icandidate；

输出：候选训练实例集Icandidate。

算法2的输入是候选源项目集和目标项目，输出是与目标项目中实例最相似的候选实例集。第1步是初始化相关数据结构，Icandidate是最终输出集合，h是要选择的候选实例集的规模。Pcc_List是存放源项目集实例与目标项目中实例间相关系数的列表；第2步是合并项目层输出的所有候选源项目的集合，得到Smerge；第3步是计算所有源项目集实例和目标项目中实例的相关系数；第4步是将相关系数和实例编号放入Pcc_List列表中；第5步是对Pcc_List列表中的相关系数值进行升序排序，最后选出排序后的前h个实例作为Icandidate。

2.3 朴素贝叶斯模型

经过两阶段的数据筛选后，已经得到了与目标项目实例集最相似的候选训练实例集，接下来就是选择合适的缺陷预测模型，本文选用朴素贝叶斯模型，朴素贝叶斯方法[20]是基于贝叶斯定理和属性条件独立性假设的分类方法，是基于软件模块中的属性值X=(x1,x2,…,x n)，得到软件模块的缺陷概率值是否最大。也就是计算：

由于朴素贝叶斯方法采用了属性条件独立性假设，即对于软件模块中所有属性，假设所有属性相互独立，那么公式可改写为：

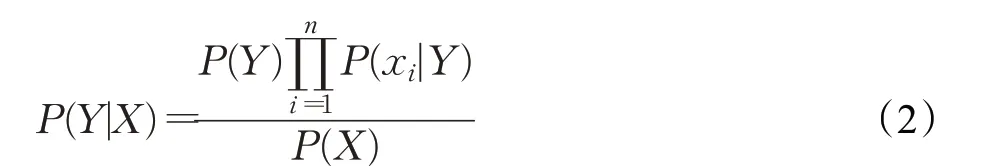
其中，Y∈{0,1}，0表示该软件模块不存在缺陷，1则表示软件模块中有缺陷。

2.4 其他预测模型

SMO[21]是一种实现支持向量机（Support Vector Machine，SVM）[22]的序列最小优化（Sequential Minimal Optimization）算法，该算法将二次型求解问题转化为多个优化子问题，并采用启发式搜索策略进行迭代求解，加快了算法的收敛速度[23]。

3 实验

3.1 实验数据

本文从PROMISE数据集中选择一部分软件项目的缺陷数据进行实验。实验所选数据是由Jureczko和Madeyski[24]收集。该数据集来自10个不同开源项目（例如ant、log4j、lucene、poi等）的多个版本。每个项目中实例的特征包括20种不同的度量元和一个缺陷数量标记，这20种度量元均关注的是代码复杂度，其中包括由Chidamber和Kemerer[25]提出的CK度量元。这些度量元综合考虑了面向对象程序固有的封装、继承、多态等特性。由于实验关注的是缺陷的分类问题，即有缺陷和无缺陷问题，因此对于数据集中的缺陷数量标记，需要把项目中缺陷数量大于0的实例标记为有缺陷标签Y，缺陷数量为0的实例标记为无缺陷标签N。所选项目数据如表1所示。

3.2 实验设计

首先在所选的软件项目中删除了少于100个实例的软件项目，目的是为了减少软件项目规模对软件缺陷预测的影响；其次需要从整理好的数据集中选择目标项目集和训练项目集。从表1中选择15个软件项目作为目标项目，如表2所示，这些项目按缺陷比可以分成三类：第一类是缺陷比大于50%的高缺陷项目；第二类是缺陷比小于10%的低缺陷项目；第三类是缺陷比在10%～50%的缺陷适中的项目。使用这些项目版本的数据进行15次跨项目缺陷预测的实验，极大地保证了实验的充分性。

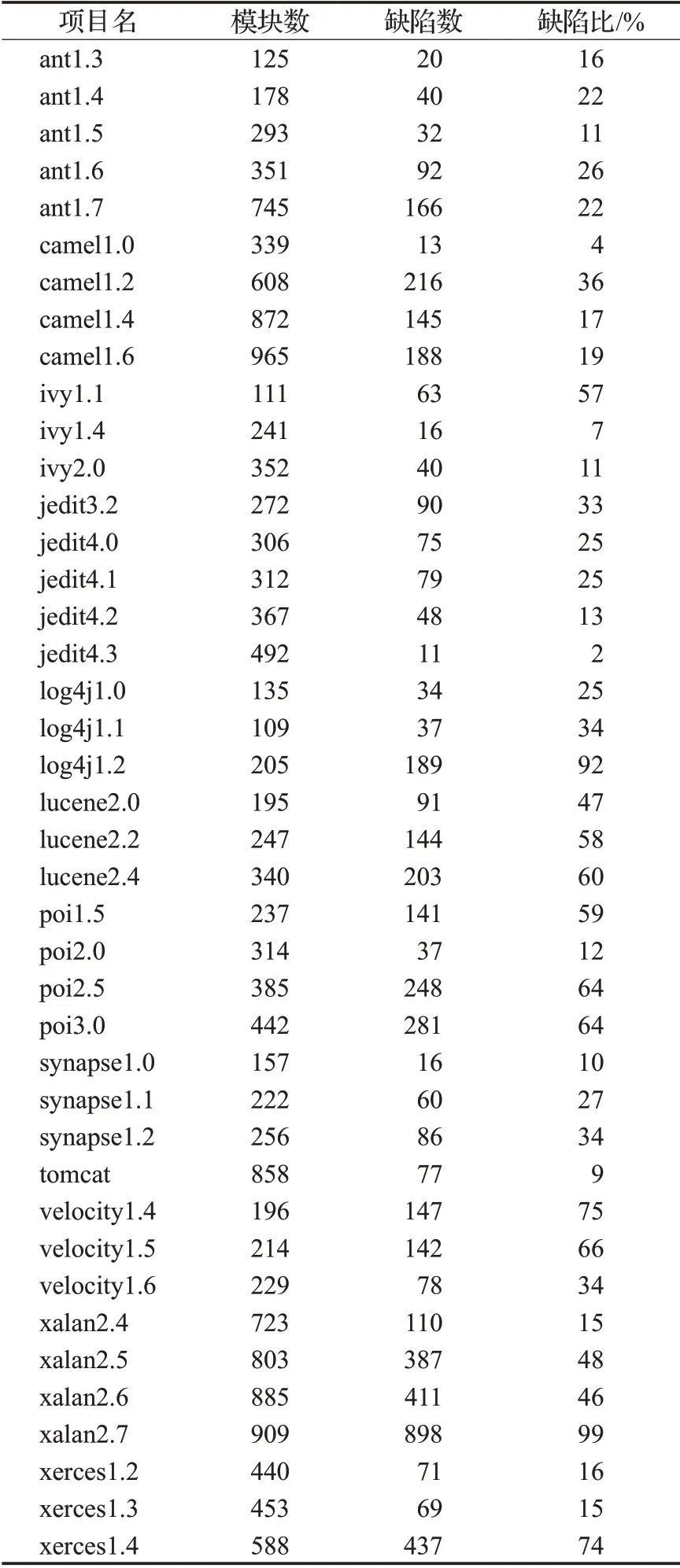
表1 PROMISE实验数据集Table 1 PROMISE experimental dataset

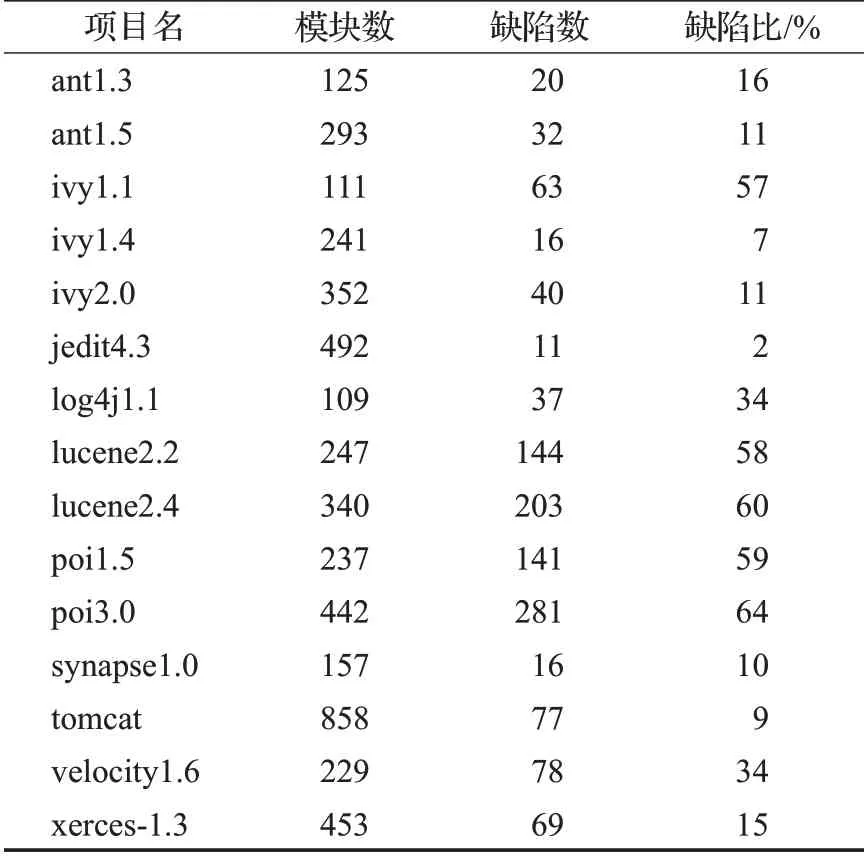
表2 目标项目集Table 2 Target projects

同时需要注意如果某一个项目作为目标项目，那么该项目同名称的其他版本不能候选源项目参与筛选。即如果ant-1.3作为目标项目，那么ant项目的其他版本不能作为候选源项目数据集，整个实验过程如图4所示。在项目筛选阶段为每个目标项目分别筛选5个候选训练项目和10个候选训练项目，即参数k=5、10；在实例筛选阶段，为目标项目里的每个实例选择5个候选实例，即参数h=5；这样进行两组不同参数的对比实验。文献[26-28]表明对于软件项目的缺陷预测，基于项目自身的历史数据或是项目的部分数据进行缺陷预测模型的训练会取得最优的性能，因此为了验证本文提出的方法的性能，在实验中选取项目内缺陷预测方法作为基准方法。在进行两组对比实验后选择效果好的一组与项目内十折交叉验证的实验结果进行比较。实验中涉及到的朴素贝叶斯缺陷预测模型在Weka平台中集成，在实验时使用默认参数即可。

图4 实验过程Fig.4 Experiment procedure

3.3 评价指标

本文关注的是目标软件项目是否存在缺陷的二分类问题，即分类的结果是有缺陷还是无缺陷。而在实际的实验中则会存在四种情况：TP（True Positive）表示有缺陷的软件项目被预测为有缺陷；FP（False Positive）表示无缺陷的软件项目被预测为有缺陷；TN（True Negative）表示无缺陷的软件项目被预测为有缺陷；FN（False Negative）表示有缺陷的软件项目被预测为无缺陷。根据这些结果进行组合产生了一些常用的性能评测指标，如准确率Accuracy、精确度Precision、召回率Recall和ROC曲线覆盖面积（Area Under Curve，AUC）等等。其中ROC曲线覆盖面积即AUC值在软件缺陷预测领域被广泛使用，同时与其他性能指标相比，AUC值更适合类分布不平衡情况下的预测的性能评价。

所以本文主要使用AUC值和Precision作为评价指标，Precision的计算如式（3）所示。由于实验是在Weka平台上进行的，所以AUC值和Precision可以直接在Weka软件的实验结果中读取，并且选取的是Weka自动加权的结果。

3.4 实验结果分析及比较

根据实验设计，首先对数据筛选算法和模型预测算法的结果进行了实验验证，其次将所得的实验结果与项目内缺陷预测的实验结果进行比较，然后对本文的实验结果进行显著性检验，进而验证提出的方法的有效性。

图5～8为不同实验参数设置下朴素贝叶斯算法和SMO算法构建的缺陷预测模型的AUC值和Precision值的箱线图对比，每个图中第一列是项目内十折交叉验证的结果，第二列是实验参数设置为k=5,h=5的跨项目缺陷预测的结果，第三列是实验参数设置为k=10,h=5的跨项目缺陷预测的结果。

图5 NB的AUC对比Fig.5 NB’s AUC comparison

图6 SMO的AUC对比Fig.6 SMO’s AUC comparison

图7 NB的Precision对比Fig.7 NB’s Precision comparison

图8 SMO的Precision对比Fig.8 SMO’s Precision comparison

由箱线图可以看出，实验参数设置为k=5,h=5和k=10,h=5的AUC值和Precision值的上下限、中间线和总体的分布比项目内十折交叉验证实验结果的箱线图要好。所以本文的方法在实验参数设置为k=10,h=5时在朴素贝叶斯模型和SMO模型上都可以取得较好的性能。此时可以初步判断出本文方法对跨项目缺陷预测的性能有提升。

为了直观比较方法中的分层筛选的算法和项目内十折交叉验证软件缺陷预测实验的结果，将朴素贝叶斯模型上两种不同实验参数设置下模型的AUC值、Precision值和项目内十折交叉验证的软件缺陷预测实验的AUC值、Precision值列于表3和表4中，最下面两行是每组实验的平均值和中值。为了更加直观地判断出性能提升的程度，将实验的结果列于表3和表4中进行对比。表中第二列是项目内十折交叉验证的预测性能，第三列是实验参数设置为k=5,h=5的跨项目缺陷预测的结果，第四列是实验参数设置为k=10,h=5的跨项目缺陷预测的结果。表中粗体数字是CPDP的性能值优于WP的。最下面两行是每组实验的平均值和中值。15组实验中，发现CPDP实验参数设置为k=5,h=5时，有8组CPDP的AUC值优于WP实验，AUC平均值提升了0.2个百分点，中值提升了0.8个百分点；CPDP实验参数设置为k=10,h=5时，有12组实验的AUC值优于WP，此时AUC平均值提升了2.9个百分点，中值提升了4.4个百分点。以Precision值超过0.7作为衡量实验成功的标志[11]，可以发现对于项目内缺陷预测实验成功率是73.3%，而对于参数设置为k=10,h=5的跨项目缺陷预测实验成功率是80%，实验成功率提升了6.7个百分点。

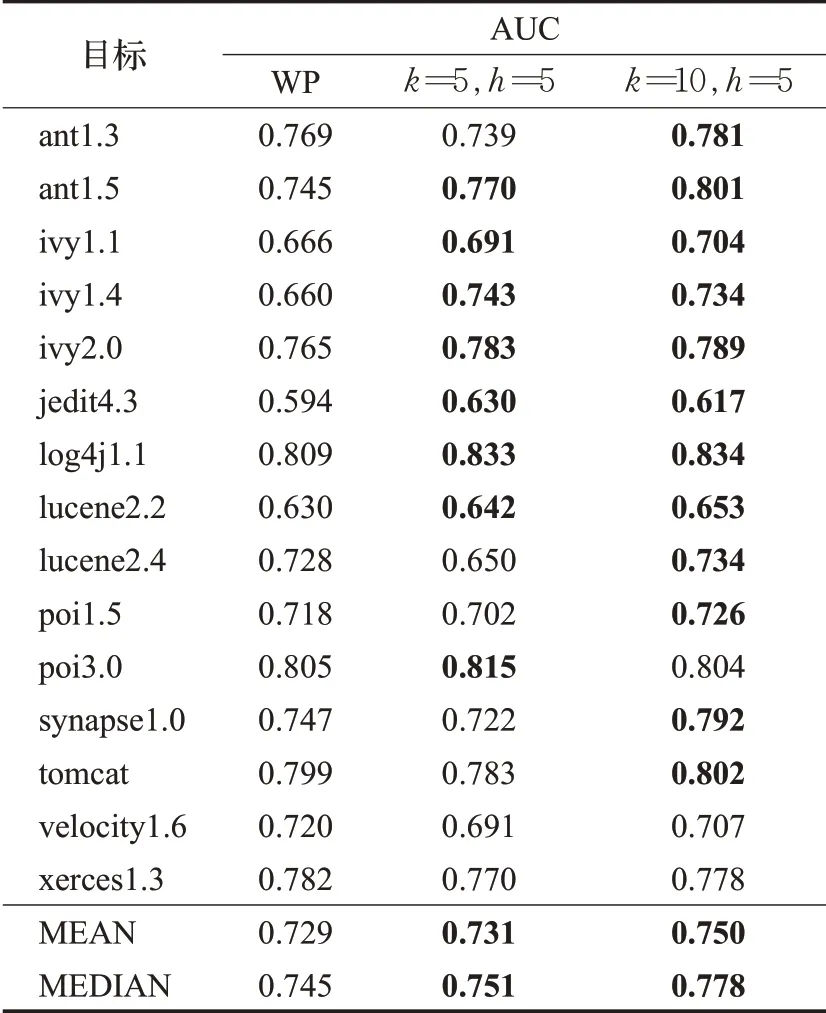
表3 NB-AUC实验结果Table 3 NB-AUC experimental results

表4 NB-Precision实验结果Table 4 NB-Precision experimental results

通过以上数据的直观比较可以得出结论：本文方法提升了跨项目缺陷预测的性能，并且与项目内缺陷预测实验相比，实验参数设置为k=10,h=5的分层数据筛选的方法取得实验结果的AUC值在中值和均值上都有明显的提高并且实验成功率同样有大幅度提升。为了进一步确定本文方法确实是优于项目内预测的实验，而不是实验产生的随机值。对CPDP参数设置为k=10,h=5的AUC值和项目内十折交叉验证的AUC值进行了Wilcoxcon符号秩检验（显著性水平α=0.05）。

Wilcoxcon符号秩检验是非参数检验，对于总体分布没有要求，因而适用范围广泛，对于实验中的两两配对样本的显著性检验，Wilcoxcon符号秩检验是解决问题的首选，它与配对样本T检验相对应。在这个实验里建立原假设H0：两种方法的预测结果来自同一个分布，即它们之间没有区别。备择假设H1：两种方法的预测结果来自不同分布，即它们之间存在显著性差异。因此，在显著性水平为0.05的情况下，如果检测的p值大于0.05则表示假设成立，接受H0；否则假设不成立，需要拒绝H0，接受H1。在Matlab上进行Wilcoxcon符号秩检验，结果输出p=0.003 2,h=1,p<0.05且p<0.01。该检验结果表明可以拒绝原假设，即提出的跨项目缺陷预测方法的实验结果与项目内缺陷预测的实验结果不是来自同一个分布，二者之间存在显著性差异。

4 结束语

本文提出了一种基于分层数据筛选的跨项目缺陷预测方法，该方法采用分层策略获取软件缺陷预测模型的训练数据并基于朴素贝叶斯算法构建软件缺陷预测模型。实验结果表明：此方法可以替代WPDP方法用于软件缺陷预测的实践，并且实验探明提出的分层数据筛选的方法在朴素贝叶斯预测模型性能最佳。

然而发现在实验过程中仍有一些地方可以继续改进：一是如何选择度量属性的分布特征尚没有统一的标准，目前为止都是依据经验选出合适的分布特征然后计算项目之间的相似性；二是在计算项目间和实例间的相似性时，时间复杂度很高，一个实验要很长时间才能得出结果；三是在衡量项目之间以及实例之间的相似性时，基本上是依据经验选用已有的相似度计算公式，在相似度计算方面还需要定义更好的计算方法；四是本文方法只在朴素贝叶斯模型和SMO模型上进行了验证，之后还需进一步在研究人员普遍使用的一些其他模型，例如线性回归、决策树和随机森立等模型上进行实验验证。以上这些实验中暴露出的问题是值得继续研究的。