基于无锚点机制与在线更新的目标跟踪算法

张 睿，宋荆洲，李思昊

北京邮电大学 自动化学院，北京 100876

目标跟踪一直是计算机视觉的一大热门研究领域，在智慧医疗、智慧城市、机器人技术等前沿科技领域都扮演着重要的角色。近年来，目标跟踪技术也有着极大发展。

目前主流的目标跟踪算法主要分为两大方向，一个主要方向是基于相关滤波的，另一个主要方向是基于深度学习的。相关滤波跟踪算法的核心是训练一个滤波模板，即分类器，用于将目标从背景信息中分离出来。Bolme等人[1]提出了最小均方误差滤波（Minimum Output Sum of Squared Error，MOSSE）。Henriques等人[2]提出了一种循环结构跟踪器（Circulant Structure Tracker，CSK）。Danelljan等人[3]提出了一种基于准确尺度评估的鲁棒跟踪算法（Discriminative Scale Space Track，DSST）。成悦等人[4]提出在相关滤波的基础上，使用加权方法融合多种特征，增强算法的鲁棒性。基于相关滤波的算法存在很多不足，如在遇到目标发生较大形变与尺度变换或背景与目标高度相似等情况时不能很好地跟踪目标，此外，该类算法需要频繁更新滤波模板，导致跟踪算法的速度变慢。

近几年，孪生神经网络的发展使得深度学习在目标跟踪上的应用产生了质的飞跃，基于孪生神经网络的系列算法也一度成为近年来最主流的目标跟踪算法，其在跟踪准确性和时效性上相比于过去的算法都有了很大的提升。Bertinetto等人[5]提出了一种基于全卷积孪生神经网络的目标跟踪算法（SiamFC），该算法接收一个尺寸较小的模板图像与一个尺寸较大的待检测图像，将两张图像同时通过上下两个完全相同的AlexNet[6]网络，生成两张特征图，然后将模板图像所得到的特征图作为卷积核，做互相关操作，在生成的响应结果图中找到得分最高的位置，再经过上采样还原成原图尺寸后，其对应的区域即为目标区域。SiamFC算法在精度和鲁棒性上较传统跟踪算法都有较大的提升，但无法应对目标尺度，形状的剧烈变化。Li等人[7]将区域建议网络（Region Proposal Network，RPN）与孪生神经网络相融合，提出了SiamRPN网络，该算法在孪生网络的基础上添加了RPN网络，直接对同一位置k个不同尺度和宽高比的锚点进行分类和位置的回归，一定程度上提高了算法在应对目标形状和尺度变化时的鲁棒性。Li等人[8]在SiamRPN的基础上提出了SiamRPN++网络，将更深层次的ResNet-50用于特征提取。Wang等人[9]提出了SiamMask网络同时实现了目标分割与目标跟踪。

SiamRPN算法难以跟踪尺度变化大，形变剧烈以及剧烈旋转的目标，主要是由于其采用了锚点机制。第一，对于锚点机制中同一位置的k个锚点，其不同的尺度和宽高比是预先设定好的，具有人为的先验知识，无法应对目标尺度和形状的变化剧烈，锚点机制中涉及到的这些超参数会很大程度影响算法的泛化性能。第二，为了提高算法的召回率，同一位置的锚点的数量要设计得足够多，这无疑增加了网络的参数量，影响了算法的时效性，同时会产生大量的负样本，造成正负样本的不均匀。第三，训练时大量的IOU计算和超参数的调整也会增加算法的训练难度。最后，SiamRPN算法是离线训练的，模型参数不会在线更新，所以当跟踪未在训练集中出现的目标时，算法的鲁棒性较差。

针对以上问题，本文提出了一种基于无锚点机制与在线更新的目标跟踪算法，提高了算法对目标旋转以及尺度与形状剧烈变化的鲁棒性，并添加了在线更新模块，使算法能更好地应对未在训练集中出现的目标，从而整体上提高算法的准确性。

1 SiamRPN目标跟踪算法

SiamRPN算法网络结构如图1所示，网络分为前后两个部分，前半部分是孪生网络即两个完全相同的AlexNet网络，负责对模板图像和待搜索图像进行特征提取，生成两个特征图，后半部分是RPN网络，负责实现对目标位置的预测。RPN网络采用了锚点机制，对原图中同一个位置k个不同尺度和宽高比的锚点进行分类和位置回归，如图2所示。RPN网络分为上下两个分支，上面的是分类分支，负责对同一位置k个锚点进行分类，由于一共分为背景和目标两类，故在最终的分类得分图中，任意位置都对应一个2k维度的向量；下面的是回归分支，负责预测k个锚点相对于目标区域的四个位置偏移量，故在最终的回归响应图中，任意位置对应一个4k维度的向量即(dx,dy,dw,dh)，其中(dx,dy)代表锚点中心点相对于目标真实区域中心点的位移，(dw,dh)代表锚点宽和高相对于目标真实区域应该缩放的比例。

图1 SiamRPN网络结构Fig.1 SiamRPN network structure

图2 RPN网络锚点机制Fig.2 RPN anchor point mechanism

网络的损失函数分为分类损失和回归损失：

其中，Lcls为分类损失，采用交叉熵损失，Lreg为回归损失，采用SmoothL1损失，λ为权重系数。

SiamRPN网络中锚点的个数以及不同锚点的尺度和宽高比都是人为预先设定好的，有大量的人为先验知识，其中涉及到的大量超参数很大程度上会影响算法的性能，即使选取了合适的超参数，算法也很难去适应目标尺度和形状的大幅度变化，同时锚点个数k很大时，会使网络参数量过大，会带来正负样本不均衡，难以训练等问题。另外，SiamRPN网络参数均为离线训练，对未在训练集中出现的目标鲁棒性也不强。

2 本文算法

本文算法的网络结构如图3所示，网络的前半部分是特征提取网络，可以有效地提取融合了不同层次信息的特征图，网络的后半段是无锚点网络，负责实现对目标位置的预测，最后本文为主干网络配备了一个在线更新模块，使网络对未在训练集中出现的目标有更好的鲁棒性，并能适应目标在跟踪过程中的变化。

图3 本文算法框架Fig.3 Framework of algorithm in this paper

2.1 多层特征融合

孪生神经网络不同深度的卷积特征所表征的目标信息有所差异，一般浅层次的特征能更好地表征图像的结构信息，深层次的特征能更好地表征图像的语义信息，良好的视觉跟踪算法一方面要根据图像的语义信息来区分不同的对象，另一方面需要图像的结构信息来精确地定位目标在图像中的位置，所以需要将不同层的卷积特征进行融合来进一步提高算法的性能。传统的SiamRPN算法仅采用了层数很浅的AlexNet网络，只能利用浅层特征所表征的结构信息，无法做到结构信息与语义信息相结合，故本文提出了一种多层特征融合方法，能更有效地将图像的结构信息与语义信息相结合。

特征融合的方式有多种，常用的方法如对不同层的特征，逐通道地在相同位置进行加权平均，从而得到融合后的特征图，该种方法未能考虑到不同通道的表现对算法的影响，使得融合后的特征表现力不足，本文为了能充分利用到不同通道的信息，在融合时采用了通道注意力机制，如图3中所示。

如图3中的特征提取网络所示，本文所采用的特征提取网络与文献[8]相同，都是改进后的ResNet-50网络，与文献[8]不同的是，本文是分别将ResNet-50中block3、block4、block5的最后一层特征先进行文献[8]中的深度互相关操作（Depthwise cross correlation），如图4，再将生成的三张特征图拼接到一起，并进行一次1×1的卷积操作，将通道数压缩为256，并将通道压缩后的特征图通过一个通道注意力模块得到最终融合后的特征图。深度互相关采用逐通道互相关的方式相比于普通互相关操作保留了不同通道的信息，相比于SiamRPN中的升通道互相关降低了参数量。

图4 深度互相关操作Fig.4 Depthwise cross correlation

本文采用了SENet[10]中的通道注意力模型，该模型可以针对不同目标自适应地学习到不同通道的重要程度，根据重要程度增强或抑制对应通道的表现，通道注意力模型如图5所示，首先对特征图进行全局的平均值池化，之后通过一个全连接层，并经过Relu函数激活，再通过一个全连接层，最后经过sigmoid函数进行归一化处理，从而得到不同通道的权重，将生成的权重与原特征图的对应通道相乘来抑制或增强不同通道的表现。

图5 通道注意力模块Fig.5 Channel attention module

2.2 无锚点机制

2.2.1 回归分支

无锚点机制最早应用于目标检测领域，如CenterNet[11]、Denet[12]、ConerNet[13]，其核心思想是直接预测目标区域中心点到目标边界的距离或直接预测出目标左上和右下角的位置。本文基于无锚点机制，设计了无锚点网络，无锚点网络分为上下两个分支，上面的为回归分支。回归分支最终输出一个25×25×4的响应图，响应图中的每个位置(i,j)都对应于其在原图感受野的中心点(x,y)，如图6所示。

图6 响应图各位置与原图中采样点对应关系Fig.6 Correspondence between response map and original graph

在训练过程中，如果点(x,y)落入目标区域，该点被标记为正样本，则该点负责预测其到目标区域边界（ground truth）的四个距离(l,t,r,b)，如图7所示。

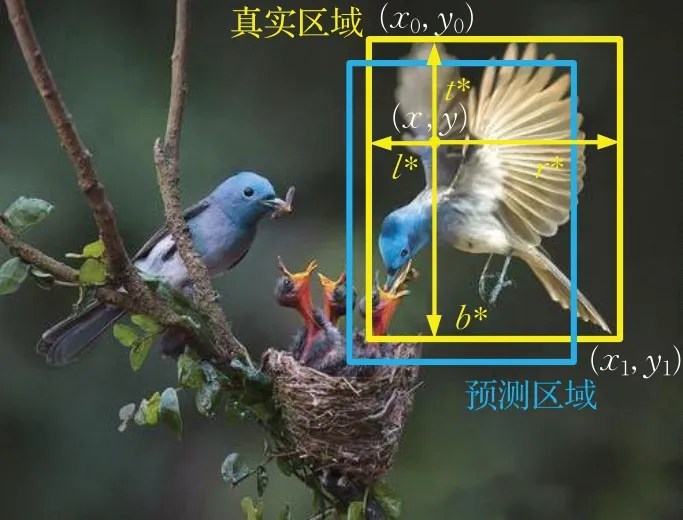
图7 回归分支预测结果Fig.7 Results of regression branch

定义目标真实区域左上角和右下角顶点坐标分别为(x0,y0)，(x1,y1)，定义k*(i,j)=(l*,t*,r*,b*)为点(x,y)到目标真实区域边界的4个距离，其中：

同理，定义k(i,j)=(l,t,r,b)为点(x,y)到预测区域边界的4个距离。

对响应图中某一位置(i,j)，若其在原图中对应的感受野中心点(x,y)落在目标区域内，则计算其对应的IOU损失，则回归分支的损失函数可以定义为：

其中：

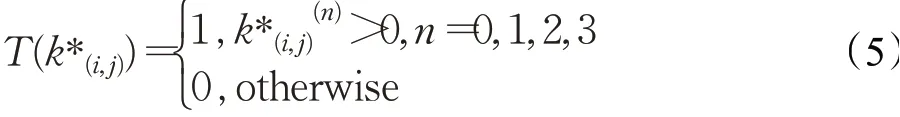
T(k*(i,j))代表点(x,y)是否落在目标区域内，若落在目标区域内则取1，反之则取0，即回归损失只计算落在目标区域内的点。LIOU(k(i,j),k*(i,j))代表预测区域与真实区域的IOU损失。

采用这种基于像素点的位置回归预测方法，可以有效地减少人为设定的超参数的数量；而且由于锚点机制预测的是某一尺度和宽高比的bounding box相对于ground truth的偏移量(dx,dy,dw,dh)，本文采用的方法是直接预测出采样点到目标区域的4个边界值(l,t,r,b)，所以能更有效地应对目标尺度和形状的剧烈变化；另外，采用这种无锚点方法也增加了正样本的数量，减少了网络的参数量，降低了算法训练的难度。

2.2.2 分类分支

无锚点网络的下半部分为分类分支，分类分支的上半部分得到一个25×25×2的分类得分图。分类得分图得到的是目标区域的大致位置。

经实验发现落在目标区域的所有采样点中，越远离目标中心的点其回归分支预测的结果越差，而越接近目标中心的点其回归分支预测的结果越好，如图8所示。如果在分类得分图中不对边缘点的得分进行抑制，会使算法的准确度大大降低。为了抑制边缘点的表现，并突出中心点的表现，本文在分类分支下引入了一个中心度分支。中心度分支会得到一张25×25×1的中心度得分图。在中心度得分图中任意位置(i,j)的响应值都对应于原图中某一采样点(x,y)的中心度。在训练过程中，中心度得分图中任意位置(i,j)的中心度C(i,j)的计算公式为：

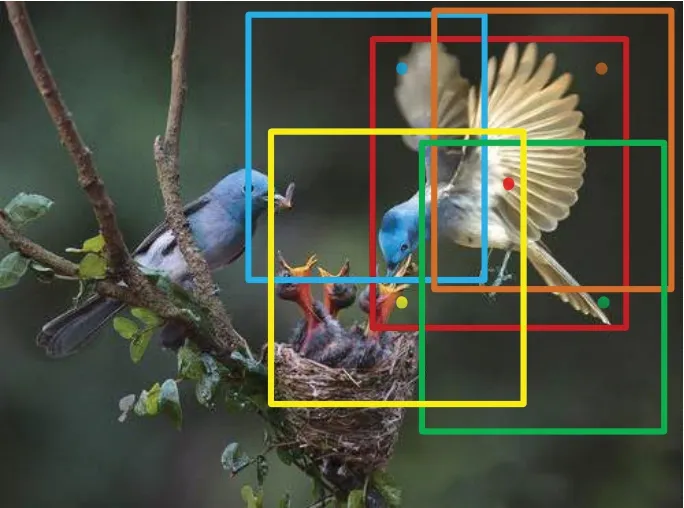
图8 目标区域内边缘点预测结果与中心点预测结果Fig.8 Prediction results of edge points and center point

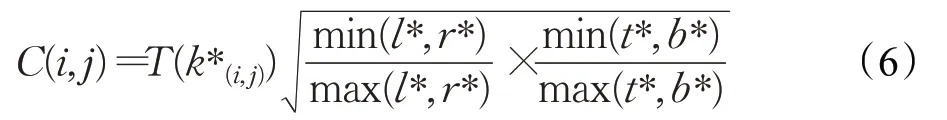
其中，min(⋅)代表取最小值，max(⋅)代表取最大值，(l*,t*,r*,b*)为(i,j)所对应采样点(x,y)到目标真实区域的四个距离，从式（6）可以看出，对于目标区域以外的采样点，中心度取0，对于落入目标区域内的采样点，越远离目标中心，其所对应的中心度得分越低，越靠近目标中心，其所对应的中心度得分越高，图9为目标区域内采样点中心度可视化图，颜色从蓝到红代表中心度从0到1，越靠近中心的采样点，其中心度越高，反之，中心度越低；测试时，将中心度得分图和分类得分图在相同位置处相乘，从而抑制边缘采样点的得分，提高算法的准确性。

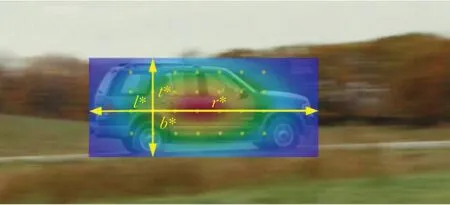
图9 目标区域内采样点中心度可视化结果Fig.9 Centrality visualization results of sampling points in target area

计算最终的分类得分时，将分类结果与中心度结果在相同位置上相乘，从而有效地对边缘点进行抑制，即最终分类分支会得到目标区域中心的大致位置。

令A(i,j)为中心度得分图上位置(i,j)的得分，中心度损失采用交叉熵损失：

分类损失Lcls也采用交叉熵损失，则总的损失函数为：

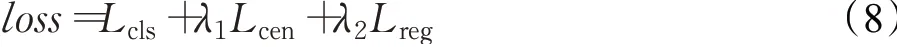
其中，λ1、λ2为权重系数，本文算法中λ1=1，λ2=3。

2.3 在线更新模块

2.3.1 在线更新模块原理

由于孪生网络都是离线训练的，在跟踪过程中模型参数不会随目标的变化而更新，所以针对未在训练集中出现的目标，不能达到最佳的跟踪效果。为了能更好地跟踪未在训练集中出现的目标，本文引入了一种在线更新模块，其网络结构如图10所示。在线更新模块利用深度回归的思想，在跟踪过程中，利用最新的视频序列作为样本，利用其对应的跟踪结果作为标签，去在线训练一个浅层的卷积神经网络，即图10中两个卷积核G1、G2，在线更新模块会直接回归出较为准确的目标中心的位置。将在线更新模块生成的结果与分类分支得到的最终结果在相同位置上加权求和，从而对分类分支得到的目标中心位置进行调整，使分类分支的结果更精确，进而可以进一步提高跟踪算法的准确性和鲁棒性。

图10 在线更新模块网络结构Fig.10 Online updating module network structure

如图3中在线更新模块所示，在线更新模块共享了主干网络中的特征提取网络，将检测分支的三个不同尺度的特征逐通道地在相同位置进行加权求和，即：

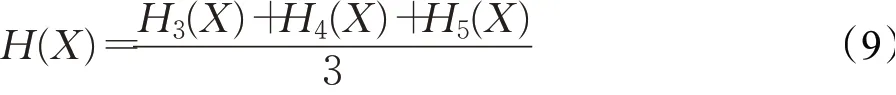
其中，H3(X)、H4(X)、H5(X)分别代表检测分支block3、block4、block5的最后一层特征H(X)为最终得到的融合特征图。将融合后的特征图先进行两次卷积操作得到一张25×25×1的分类结果图，并与分类分支得到的最终结果进行加权求和：

其中，ponl为在线更新模块得到的结果，pcls为主干网络的分类结果，pcen为主干网络的中心度结果，ω为权重系数，本文实验中ω取为0.5，ω不同取值对实验结果的影响可参见3.4小节。在线更新网络可以抽象定义为：

其中，x为输入的特征图即H(X),ω1、ω2分别为1×1卷积和7×7卷积的权重，ϕ1、ϕ2为激活函数，∗代表标准的卷积运算，f(x;ω)为最终的回归结果。在线更新模块的模型参数是在跟踪过程中在线训练并更新的，其损失函数定义为：

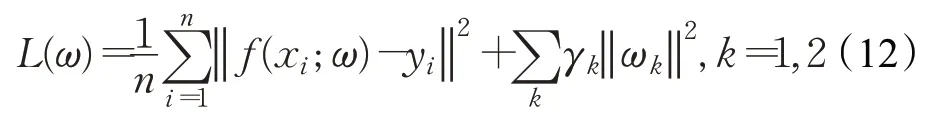
其中，i代表样本的编号，ωk分别代表1×1卷积(k=1)和7×7卷积(k=2)的权重，yi为第i个样本所对应的标签值为防止过拟合采用的正则项。

样本标签采用高斯标签。在跟踪初始时将初始帧进行数据增强，对其进行相应的旋转、偏移、模糊等操作，生成30张训练样本，同时得到30张样本标签，如图11所示。利用训练样本同时对G1、G2进行训练。之后每隔15帧训练一次，将这15帧的图像序列作为训练样本只针对G2进行训练，以应对目标在跟踪过程中的变化。

图11 部分初始帧数据增强后样本及其高斯标签Fig.11 Part of initial frame data enhanced sample and their Gaussian labels

2.3.2 牛顿-高斯混合共轭梯度法

为保证算法的实时性，在线训练过程要尽可能地快，由于传统的随机梯度下降算法收敛慢，无法满足跟踪算法的实时性要求，受文献[14]的启发，本文采用一种牛顿-高斯混合共轭梯度的方法进行模型的在线训练，采用这种方法，训练时可以在经过较少次数的迭代后就实现收敛。

针对第i个样本其损失函数为：

其中，i代表样本编号，y i为第i个样本所对应的标签值，f(x i;ω)为第i个样本的回归结果。

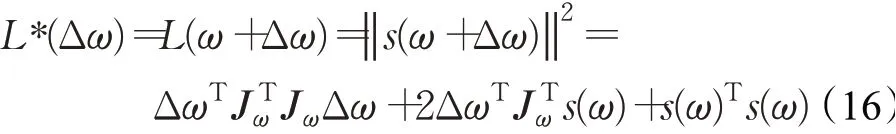
其中，Jω为参数ω的雅克比矩阵。为了求得Δω使得L*(Δω)极小，应该对上式求导，进而得迭代公式ω=ω+Δω。为了避免求逆，且式（16）满足共轭梯度法求解形式，本文采用共轭梯度法求Δω，共轭梯度法的思想是，选择一个优化方向后，选择一个步长对参数进行更新，且选择的步长应能将这个方向的误差更新完；共轭梯度法相较于传统梯度下降法可以更快地到达L*(Δω)的极小值点，进而整体上使算法的收敛速度更快。

共轭梯度法的核心是求出每次迭代时的优化方向和步长。每次迭代选择的优化方向p k的更新公式为：

其中，k代表第k次迭代，gk代表第k次迭代L*(Δω)对Δω的梯度。

每次迭代的优化步长αk为：

每次迭代的梯度g k的更新公式为：

详细的共轭梯度法的推导和证明过程以及其较梯度下降法的优势不在本文的讨论范围内，感兴趣的读者可参见文献[14]。

算法伪代码为：

其中外层循环是牛顿-高斯法，迭代更新ω，共迭代NGN次，内层循环是共轭梯度法，共迭代NCG次。每次进如外层循环时，先进行初始化操作。进入内层循环后，对于内层循环的第k+1次迭代，计算优化方向pk+1，之后计算步长α，并更新梯度g和Δω。经实验，本文取NGN=6,NCG=10，此时在线训练可以大致达到速度与精度的平衡。

2.4 跟踪过程

在线跟踪时，第一帧先选定目标区域，之后将得到的目标区域作为模板图像，后续的视频帧作为待搜索图像，送入到本文算法的网络中，在最终的分类得分结果图中选取得分最高的点，再在与其相邻的n个点中选取得分前k大的三个点，分别计算回归结果中这k+1个点（包含最大值点）所对应的四个边界值(l,t,r,b)的平均值即为跟踪结果。本文实验中n取8，k取3。跟踪初始时对初始帧进行数据增强，生成对应的样本和标签送入到在线更新模块进行训练，之后每15帧对模型进行一次更新。

3 实验

3.1 算法训练细节

本文是在Windows平台，利用Pytorch进行算法的测试和训练，利用Nvidia RTX2080Ti显卡进行计算加速。模板分支输入图像尺寸为127×127，测试分支输入图像尺寸为255×255。对于离线模型，训练时采用随机梯度下降法，每个batch的大小为96，一共训练20个epoch，对于前10个epoch，冻结前半部分孪生网络的参数，单独训练后半部分的分类分支和回归分支，对于后10个epoch，解冻Resnet-50的后三个block的参数，训练时采用的训练集为Youtube-BB[15]、ImageNet VID、ImageNet DET[16]以及COCO[17]。

3.2 OTB100测试集实验结果对比

OTB100[18]测试集包含了100个极具挑战和代表性的视频，这些视频分别体现了目标在跟踪过程中一定程度上的形变、旋转、尺度变化以及跟踪过程中背景模糊，光照变化等因素。OTB100的评价指标为成功率与准确率，其中成功率指预测区域与目标真实区域重叠率大于一定阈值的帧数与总帧数的比值，准确率指的是预测区域中心与目标真实区域中心位置误差值小于某一阈值的帧数占总帧数的比值。本文利用OTB100测试集对本文算法与目前主流的几种跟踪算法进行对比，包括SiamRPN、SiamFC、ECO-HC[19]、SRDCF[20]、STAPLE[21]、DSST[3]、KCF[22]。图12为OTB100下不同算法成功率与准确率曲线图，从图12中可以看出，本文算法在成功率和准确率上相较于目前主流的跟踪算法，都有较大的提升，本文算法相较于基线SiamRPN算法，成功率提升了0.062，准确率提升了0.065，相较于基于相关滤波的算法ECO-HC成功率提升了0.065，准确率提升了0.074。图13为OTB100中尺度变化、形变以及旋转三种不同属性视频下准确率和成功率曲线图，从图13中可以看出本文算法在应对目标尺度变化、形变以及旋转时，都有最好的表现，其准确率和成功率较基线SiamRPN算法都有较大的提升，这主要得益于无锚点机制对目标变化的适应能力以及在线更新模块对新目标的鲁棒性。

图12 OTB100数据集中各算法准确率与成功率Fig.12 Accuracy and success rate of each algorithm in OTB100

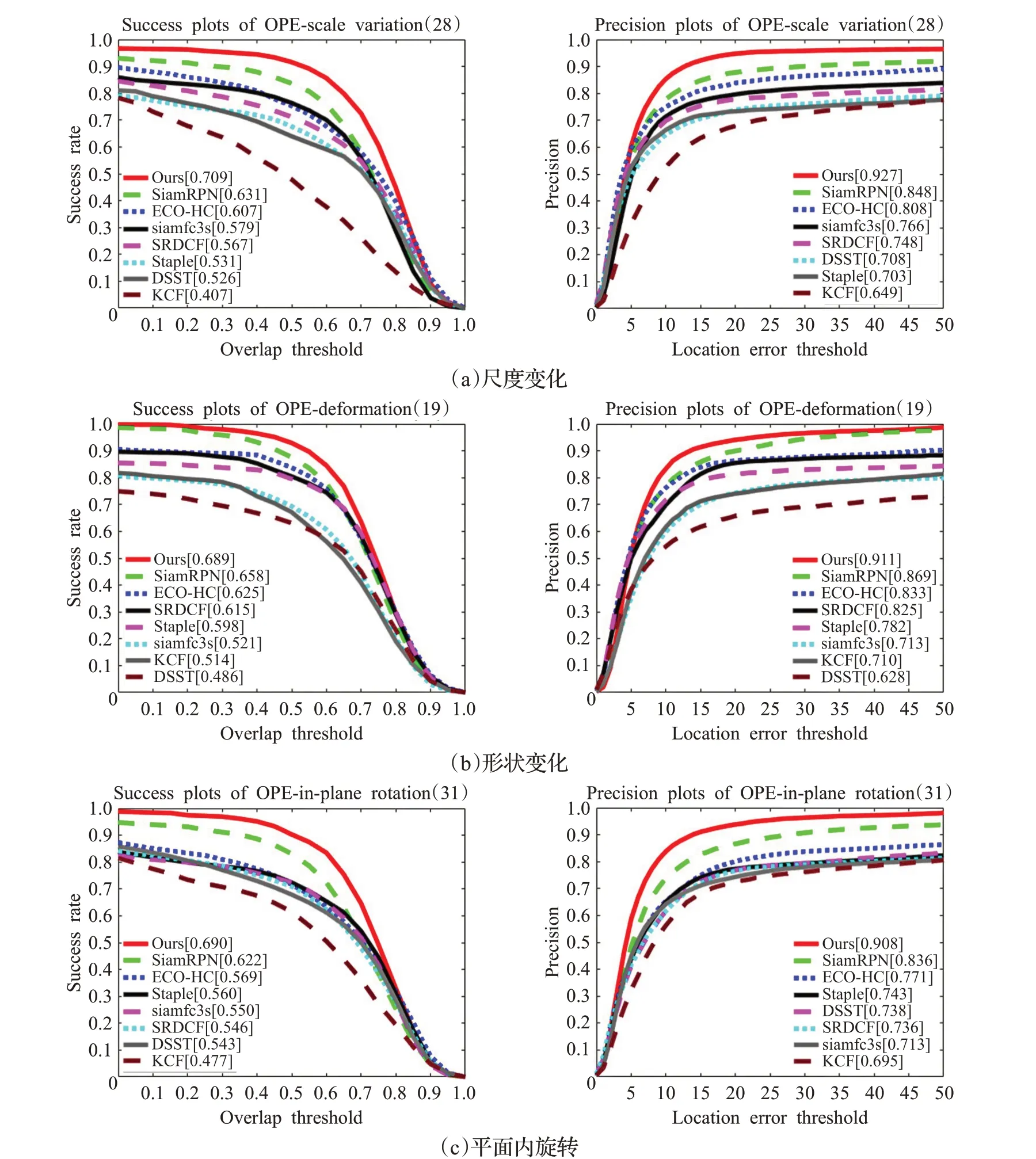
图13 OTB100中各算法在目标尺度变化、形变与旋转情况下准确率与成功率Fig.13 Accuracy and success rate of each algorithm in OTB100 when target scale changing，deforming and rotating

3.3 VOT2018测试集实验结果对比

VOT Benchmark[23]是一个评测视觉目标跟踪算法性能的测试平台，其主要评测指标包括精度（A），鲁棒性值（R）和期望平均重叠值（EAO）。精度表示算法预测区域与目标真实区域的重叠率，鲁棒性表示算法在视频序列中的失败情况，期望平均重叠值是算法的综合性能指标。精度和期望平均重叠值越大，说明算法的精确度越优秀，鲁棒性越小，说明算法失败的次数越少，更能应对复杂的场景。为了进一步验证本文算法的有效性，本文利用了VOT2018测试集对本文算法与另外几种主流跟踪算法进行对比，包括SiamRPN、DaSiam-RPN[24]、SA_Siam_R[25]、UPDT[26]、CRPN[27]、ECO[19]，其对比结果见表1。从表1中可以看出本文算法相较于基线SiamRPN算法精度提高了0.011，期望平均重叠值提高0.084，鲁棒性提高了0.108，在所对比的算法中精度、期望平均重叠值最高，鲁棒性最低，说明本文算法在跟踪的准确性上具有最好的效果，且对目标变化的鲁棒性最好。在跟踪的时效性上，本文算法可以达到43 frame/s，较SiamRPN算法低，一是因为本文特征提取网络层数深，二是因为本文包含的在线更新模块需要在线训练，所以总体上速度会降低，但仍能基本满足实时性需求。

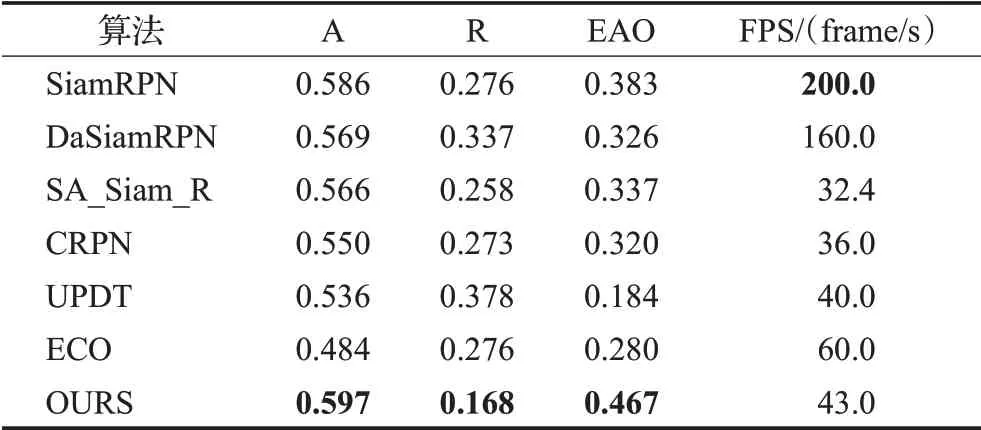
表1 VOT2018上几种主流算法性能对比Table 1 Comparison of different algorithms on VOT2018

3.4 消融实验

为说明本文算法的有效性，分别测试了算法在具备不同组件时其在OTB100数据集上的表现，实验结果如表2所示。从表2中可以看出，算法1不具备任何组件，其跟踪效果最差；算法2缺少了中心度分支和在线更新模块，成功率为0.613准确率为0.819，均不如SiamRPN（成功率0.635，准确率0.853），主要原因是在分类结果中没有对目标区域内边缘点的得分值进行抑制，使得算法总体的准确度和成功率大大降低。

表2 算法具备不同组件时在OTB100上的成功率与精确率Table 2 Performance of algorithm with different components on OTB100

算法3在算法2的基础上增加了中心度分支后，在分类结果中对边缘的得分进行了抑制，突出了中心点，从而使算法的成功率和准确率都得到了提高。

算法4在算法3的基础上添加了在线更新模块，使算法的成功率和精确度得到了进一步的提高，主要原因是在线更新模块可以利用最新的跟踪结果直接回归出目标的中心位置，提高了目标中心区域的定位精度，进而总体上提高了算法的准确度，并且由于利用了最新的跟踪结果对网络不断更新，也使算法能更好地适应目标的变化。

为验证在线更新模块中权重系数ω对算法性能的影响，本文测试了ω取不同值的情况下算法在OTB100数据集上的表现，实验结果如图14所示。从实验结果可以看出，当ω>0时，算法的成功率和准确率都要比ω=0时大，说明在线更新模块确实会一定程度上对分类分支得到的目标中心位置进行调整，从而使算法性能有不同程度上的提高。从图14中可以看出当ω=0.5时算法的成功率和准确率最高，说明此时，在线更新模块对分类分支所得结果的调整程度最恰当，最终得到的目标中心位置最准确，故算法整体上性能最好，所以本文算法中ω取0.5。

图14 OTB100数据集下ω不同取值对算法的影响Fig.14 Impact of differentωon performance of algorithm in OTB100

为验证本文算法多层特征融合时采用通道注意力机制的优越性，本文在进行多层特征融合时，分别采用了通道注意力机制与加权平均两种方式，并对这两种融合方式在OTB100数据集上进行了对比实验，实验结果如表3所示，实验表明采用通道注意力机制的方法较另一种方法准确率提高了0.016，成功率提高了0.008，这是由于采用逐通道相同位置元素加权平均的方法没能充分考虑到对于不同目标，不同通道有不同表现力这一特性；而通道注意力机制可以自适应地学习到不同通道的权重，针对不同目标增强或抑制不同通道的表现，从而整体上使算法性能得到进一步的提升。

表3 不同多层特征融合方式下算法性能对比Table 3 Performance of algorithm with different multi-layer feature fusion method

3.5 跟踪效果分析

为了更直观地表现本文算法对目标旋转、形变与尺度变化的鲁棒性，本文选取了OTB100数据集中几个典型视频序列的跟踪结果，如图15所示。

图15 典型视频序列上各算法跟踪结果对比Fig.15 Comparison of different algorithms on typical video sequences

图15（a）、（b）两个视频序列体现了目标在跟踪过程中的尺度变化。在（b）视频序列的第1 048帧，目标的尺度发生了巨大的变化，从图15中可以看出，本文算法较其他算法跟踪的效果最好，主要是因为本文算法采用了无锚点机制，能够直接回归出目标中心点到目标区域边界的4个距离，所以能更好地应对目标的尺度变化。而SiamRPN算法只是将设定好的锚点进行一定程度的偏移和缩放，SiamFC等算法更是缺少尺度自适应机制，故这些算法只能跟踪到目标的局部，跟踪效果较差。

图15（c）、（d）两个视频序列体现了目标在跟踪过程中的形状变化。在（c）视频序列的第648帧，目标的形状发生了剧烈变化，从图15中可以看出，本文算法的跟踪效果最好，其他算法都发生了一定程度上的漂移，一方面是因为本文采用了无锚点机制，能更好地应对目标形变，另一方面由于本文配备的在线更新模块能一定程度适应目标的变化，从而进一步提升了算法对目标形变的鲁棒性。

图15（e）、（f）两个视频序列体现了目标在跟踪过程中的旋转。在（f）视频序列的第180帧，目标发生了较大的旋转，从图中可以看出，本文算法的跟踪效果最佳，其他算法跟踪到了目标的局部或发生了一定的漂移，这说明本文的无锚点机制和在线更新模块对目标旋转有一定程度的自适应能力。

4 结语

本文提出了一种基于无锚点机制与在线更新的目标跟踪算法，对现有的SiamRPN算法做出了改进。本文首先提出了一种多层融合的特征提取网络，使网络能充分利用图像的结构与语义信息；其次基于无锚点机制设计了无锚点网络，直接预测目标区域内采样点到目标区域边界的四个值，有效避免了锚点机制的相关缺点，对跟踪过程中目标的形变、旋转与尺度变化有更强的鲁棒性；最后，在孪生网络的基础上添加了在线更新模块，利用最新的跟踪结果去在线训练一个浅层的网络，一方面能更好地预测未在训练集中出现的目标，另一方面可以使算法适应目标的变化。本文利用OTB100与VOT2018两个测试集对本文算法与几种主流的跟踪算法进行对比，相较于SiamRPN算法，在OTB100数据集上本文算法在成功率与准确率上提高了0.062与0.065，对目标的形变、旋转以及尺度变化表现出了更良好的鲁棒性。