基于旋转电机统一模型实现考虑动态负荷的多机系统短路电流衰减计算

黄阮明，曹 炜，张 铭，郭明星，何必伦

（1.国网上海市电力公司经济技术研究院，上海 200233；2.上海电力大学电气工程学院，上海200090）

随着经济发展与社会进步，电力系统负荷持续提高，装机容量也迅速增长，电网互联日益加强，使得部分地区计算的短路电流水平超标问题日益突出[1-6]，虽然采取了各种限流措施，电网中仍有些断路器开断能力裕度很小，这就需要更加精细地计算短路电流，不但要计算短路电流的初始值，还要计算短路电流的衰减。

由于输电网短路电流计算标准[7]导向的原因和历史上断路器的开断能力裕度曾经比较大，目前输电网短路电流只计算周期分量的初始有效值且计算时基于经典假设不考虑负荷的影响[8]。如果负荷中只有静态负荷（以ZIP模型为代表），这样做是合理的，因为静态负荷有分流作用[9]。但随着电网中动态负荷比例的增加，完全不计负荷将使计算所得的短路电流周期分量初始有效值偏小[9-11]；而如果考虑动态负荷计算周期分量却不考虑其衰减，又将比较严重地高估断路器触头刚分时周期分量的实际值。

计算曲线法是传统计算短路电流周期分量衰减的方法。该方法不考虑汽轮发电机间、水轮发电机间个体参数存在的差别，且假设所有发电机在额定满载工况下带静态负荷，带来较大的计算误差[4，12-13]。

文献[4]总结了目前主流电力系统仿真软件中的短路电流计算模块功能，可概括为三类，一类为可以考虑动态负荷，但只计算短路电流周期分量初始有效值，而不考虑其衰减，如PSD软件SCCP模块；另一类为可以考虑周期分量衰减，但不考虑动态负荷的影响，如PSS/E软件BKDY模块[14]；再一类为既不考虑动态负荷又不考虑周期分量的衰减。

近些年，一些学者注意到动态负荷反馈电流对短路电流产生的影响，并做了一定的研究。文献[10]分析了包括感应电动机在内的综合负载模型对短路电流计算的影响；文献[11]研究感应电动机负载对输电网短路电流初始值的影响；文献[4，15]介绍了如何在PSS/E电力系统仿真软件的潮流数据卡中将电动机所在节点设为PV节点，完成考虑动态负荷的短路计算，但该方法需要改变原软件已输入的基础数据，影响其潮流、暂态稳定功能的正常使用[4]。

本文统一考虑旋转电机，首先通过将单机系统短路电流周期分量衰减代数表达式转化为发电机、感应电动机（由动态负荷等效）电势衰减的代数式，再借鉴机电暂态计算的坐标变换使代数表达的衰减的旋转电机电势能够参与电网方程，最后线性代数求解电网方程，得到多机系统短路电流周期分量的衰减，避免了像机电暂态仿真那样求解微分方程。本文方法所得结果与机电暂态仿真所得短路电流周期分量相比误差很小，远小于传统计算曲线法的误差[13]，且本文方法可以考虑动态负荷对短路电流周期分量衰减的影响。

1 考虑动态负荷的短路电流衰减实用计算原理

本文计算短路电流衰减的方法基于网络节点电压方程，变单台发电机短路电流衰减计算公式为发电机电势的衰减计算公式，再通过坐标变换使短路后衰减的发电机电势作用于复杂网络，用该网络的节点电压方程计算各节点电压的衰减，最后计算短路点电流的衰减。

1.1 单机系统中旋转电机衰减电势代数表达式

1.1.1 发电机衰减电势的推导

单台发电机在其出口支路短路时的电路如图1所示，忽略回路电阻，其短路电流可表示为

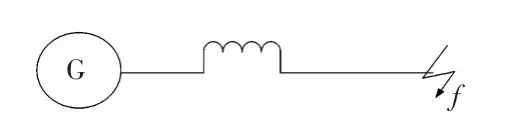
图1 单台发电机短路示意Fig.1 Schematic of single-machine short-circuit

式中，id0为发电机短路前瞬间定子绕组d轴电流。

将式（3）代入式（1）再代入式（5）整理得当q轴

1.2 衰减电势通过坐标变换作用于网络方程

由于式（6）～（10）是以每台机各自的dq轴为参照系列写的电势衰减代数模型，该模型需经坐标变换作用于网络方程，构成整个电力系统的线性代数模型，如图2所示，用于后续的短路电流计算。

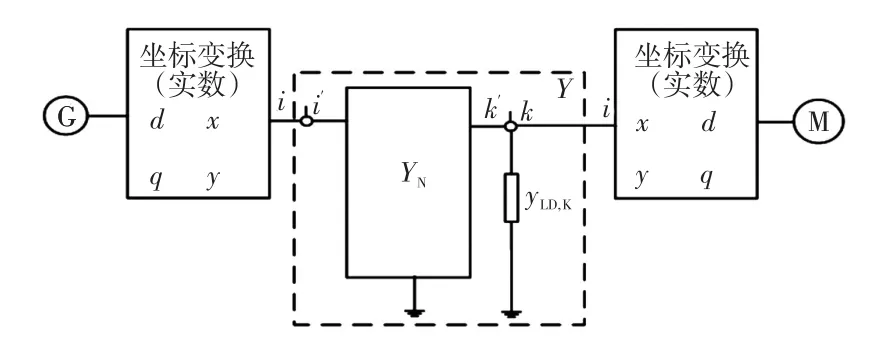
图2 网络方程与旋转电机数学模型的关系Fig.2 Relationship between network equation and the mathematical model of rotating machine

1.2.1 网络方程

设潮流计算对应的节点电压方程为

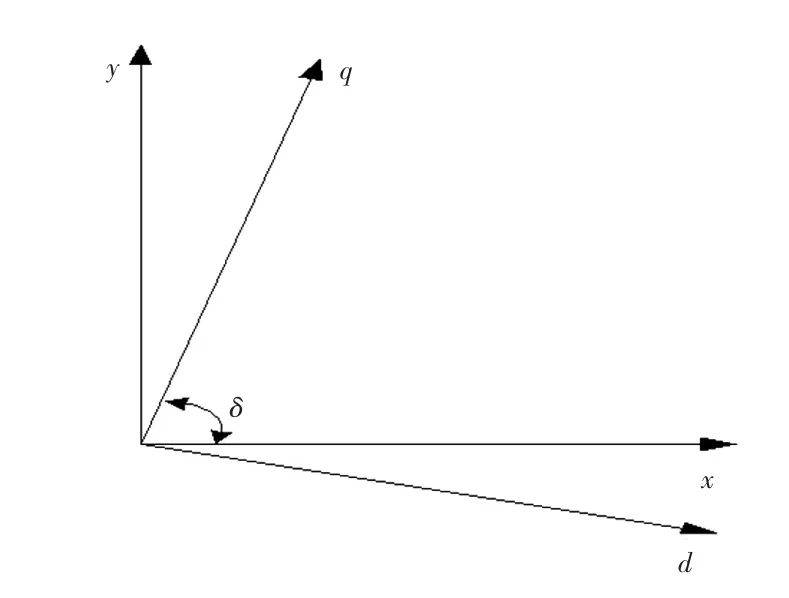
图3 坐标变换关系Fig.3 Relationship of coordinate transformation

1.2.3 发电机衰减电势经坐标变换作用于网络方程

计及发电机阻尼绕组影响时，计算其节点对电网的注入电流，按固定在电机转子上的dq坐标系建立电压方程，其矩阵形式为

单鼠笼感应电动机的网络修正系数方程以及节点注入电流方程只需将双鼠笼感应电动机对应方程中的次暂态参数变为暂态参数。

1.3 衰减电势表达式中短路点电气距离Xe的计算

为了利用上述单台机出口支路短路时的电势衰减式（6）～（10），需将旋转电机间网络状的联系（如图4所示）简化为以短路点为中心、向各旋转电机辐射的连接关系（如图5所示）。而在图5中，旋转电机端到短路点的电气距离可近似用式（26）求取

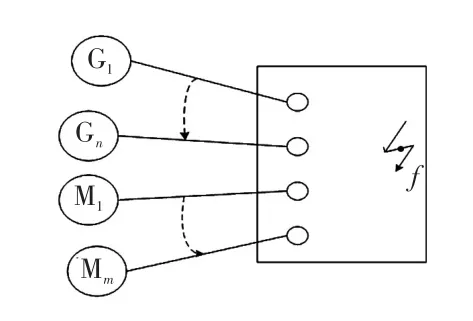
图4 复杂网络Fig.4 Complex network

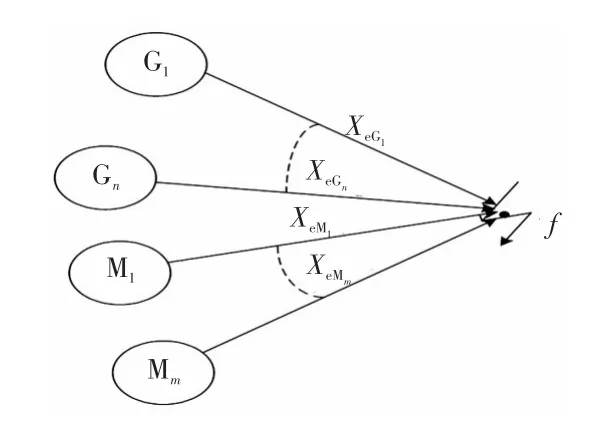
图5 简化网络Fig.5 Simplified network

式中：Vx、Vy分别为电机机端电压的正、虚轴分量；Ix、Iy分别为电机定子电流的正、虚轴分量。

2 短路电流衰减计算程序设计与实现

本文分3个模块实现对多机系统短路电流衰减的计算，即数据输入模块、短路电流计算模块及动态链接库，图6所示。数据输入模块基于PSS/E数据平台进行设计，可以方便地使用电网企业精心维护的非常可靠的电力系统潮流和暂态稳定基础数据进行大电网的短路电流周期分量计算，同时便于用PSS/E暂态稳定模块在短路情况下输出的电流数据校核所编软件计算出的短路电流衰减的正确性。通过动态链接库[16]将本文方法模块融入PSS/E人机界面。与文献[4]和文献[15]所述方法不同，本软件使用时，不需改变PSS/E数据平台的数据结构和输入数据值，所以不影响其原有潮流计算、稳定计算功能的使用。

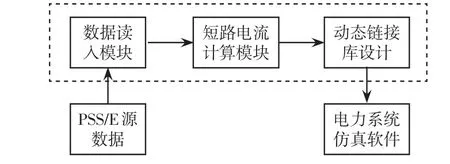
图6 短路电流计算模块结构Fig.6 Structure of short-circuit current calculation module

3 算例分析

针对某大都市电网，应用所编短路电流计算程序对其分别进行考虑和不考虑负荷动态特性的短路电流（周期分量）衰减计算，并与同样负荷模型[17]下的PSS/E机电暂态仿真结果进行比较。

分别应用本文短路电流实用计算模块和PSS/E机电暂态稳定计算模块对某大都市电网某故障点进行考虑和不考虑负荷动态特性的短路电流衰减计算，结果如表1、图7所示。

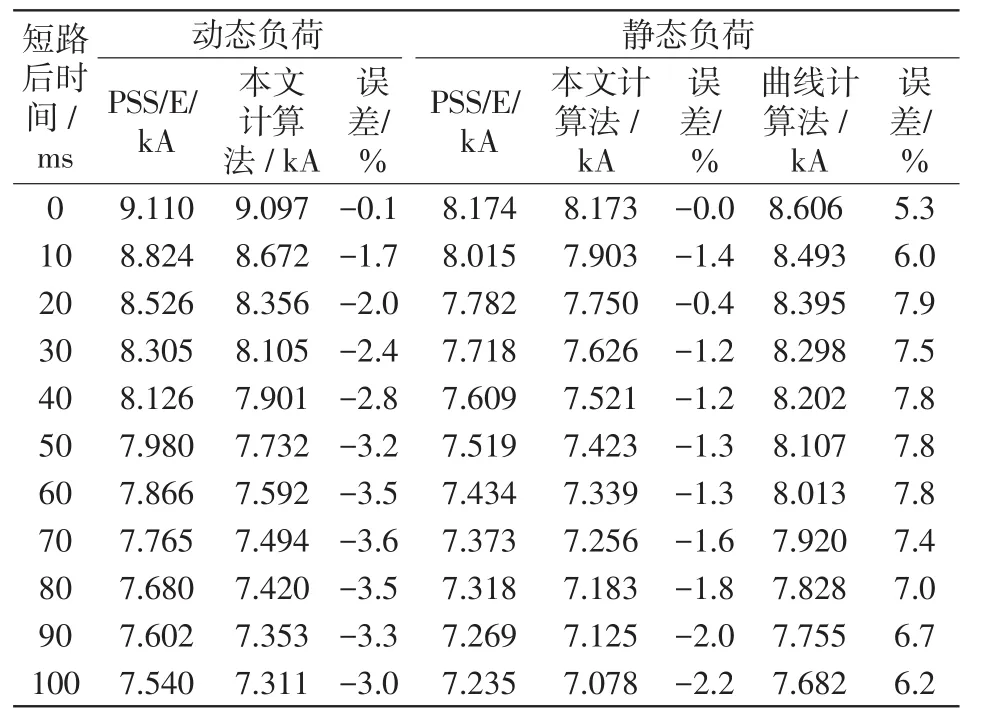
表1 三相短路电流周期分量衰减情况Tab.1 Decay of periodic component of three-phase short-circuit current

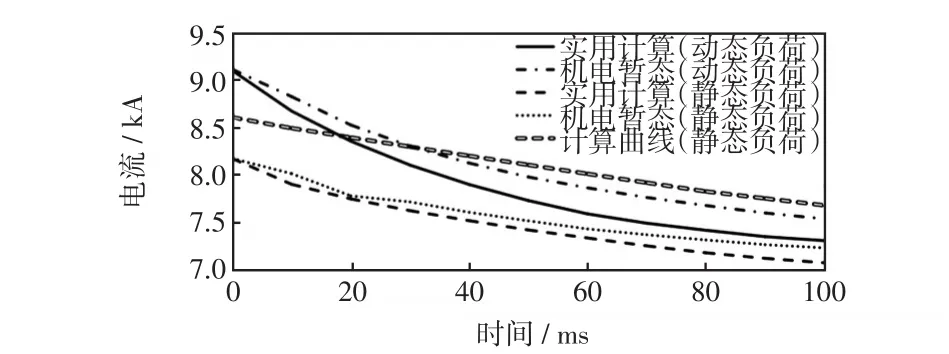
图7 三相短路电流周期分量衰减Fig.7 Decay of periodic component of three-phase shortcircuit current

为了和计算曲线法进行结果比较，参照文献[18]编程实现了计算曲线法，由该法所得结果也如表1、图7所示。

从表1、图7可以得出以下几点：

（1）无论是否考虑动态负荷，实用计算和PSS/E机电暂态计算结果非常接近；在计算时间0～100 ms内，计算结果相差率最大不超过4.0%；其中短路电流初值（0 s时刻）两种计算方法相差小于0.15%。

（2）考虑动态负荷特性以后，电动机对短路电流的反馈非常明显，与不考虑动态负荷时相比，使短路电流短路瞬间增大10%以上，其后增大效果随着电动机反馈电流的衰减逐渐减小。因此考虑动态负荷后周期分量衰减明显快于不考虑周期分量时，也快于不考虑动态负荷的曲线计算法（在曲线的制作过程中，负荷“用恒定阻抗表示”[12]）所得计算结果。

对多条母线进行了三相短路电流的衰减计算，其结果均符合上述结论。

对表1、图7中各曲线数据进行拟合，得其衰减时间常数如表2所示。

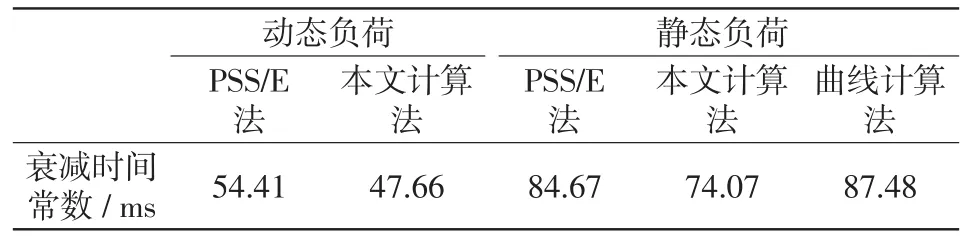
表2 三相短路电流周期分量等效衰减时间常数Tab.2 Equivalent attenuation time constant of periodic component of three-phase short-circuit current

4 结语

短路电流周期分量的衰减源自旋转电机转子绕组磁链的衰减，基于此提出了基于潮流详细考虑旋转电机对短路电流影响的短路电流周期分量衰减实用计算方法。本方法采用坐标变换，能详细考虑发电机不同轴向上的绕组，同时也用感应电动机模型考虑了动态负荷对短路电流及其衰减的贡献。基于本方法所编程序能够计及短路前电力系统的运行状态、动态负荷、不同容量型号发电机的实际情况，计算短路后电流周期分量任意时刻的值，使对断路器断流能力的校核更有现实依据，适合在断路器开断能力裕度较小时应用。

所编软件使用了商用电力系统分析软件PSS/E的潮流和机电暂态数据平台，以便使用电网企业精心维护的非常可靠的电力系统潮流和暂态稳定基础数据进行大电网的短路电流周期分量衰减计算，而不需要另外维护一套计算数据；同时便于用PSS/E暂态稳定模块在短路情况下输出的电流数据校核所编软件计算出的短路电流衰减的正确性。

以某大都市电网为案例，对比了本文实用计算方法所得、PSS/E机电暂态仿真计算所得结果，计算结果相差率最大不超过4.0%。

也可基于其他软件（如BPA、PSASP）数据平台编程实现本文所述方法。