基于改进蝠鲼觅食优化SVM的配电网拓扑辨识

叶剑华，罗凤章，杨 理

（1.天津职业技术师范大学，天津市信息传感与智能控制重点实验室，天津 300222；2.天津大学智能电网教育部重点实验室，天津 300072；3.国网重庆永川供电公司，重庆 402160）

随着智能配电网的发展，分布式电源DG（dis⁃tributed generation）在配电网中的部署规模越来越大，配电网的开关状态变化日趋频繁，这对配电网的管理提出了挑战，需要快速有效地识别配电网的实时拓扑结构。因此配电网拓扑辨识是一个具有重要意义的研究课题。

输电网具有完善的数据采集与监控SCADA（su⁃pervisory control and data acquisition）系统，配置了大量的冗余量测，调度人员可实时获取网络的拓扑结构，并采用状态估计识别拓扑错误。配电网的特性使得拓扑辨识更加困难。首先，配电馈线和开关数量众多，特别是在区县农村配电网，出于投资和成本等因素的考虑，目前的配网自动化水平普遍不高，量测不能全部覆盖，其监测设备和通信链路有限，运行人员不易掌握线路和开关的实时状态。随着分布式电源、可控负荷和电动汽车的接入，保护和开关动作更加频繁，使得配电网的拓扑结构更加多变[1]。

配电网拓扑辨识方法主要有两大类。第一类是基于配电网网络参数和结构的数值优化方法。文献[2]提出了一种基于混合整数二次规划MIQP（mixed integer quadratic programming）的配电网拓扑辨识方法，将最小化测量残差的加权平方和作为拓扑辨识模型的目标函数，用于辐射状配电网。文献[3]利用微型同步相量量测单元μPMU（micro-syn⁃chronous phasor measurement unit）获取节点注入功率的多次采样值，计算基于节点注入功率量测的电压偏差的方差，将其作为线路的权重，采用Kruskal算法构造方差最小的最小生成树，相应的结构即为配电网的运行拓扑。文献[4]基于匹配环路功率确定可能的拓扑结构，并根据共同量测值对可能的拓扑结构进行状态估计，将状态估计值与量测值有最高匹配度的拓扑结构作为实际拓扑结构。文献[5]先通过μPMU对其安装位置的电压相位进行量测，确定拓扑变化时刻，再枚举出重构后的所有可能拓扑，将μPMU和配电网SCADA（DSCADA）的量测数据进行融合，对所有可能拓扑进行状态估计，比较节点估计电压相位和μPMU实测电压相位，确定实际的拓扑结构。文献[6]提出了一种基于高级量测体系AMI（advanced measurement infrastructure）潮流匹配的辐射状中压配电网两阶段拓扑辨识方法，首先采用MIQP模型进行初步拓扑辨识，在此基础上，采用图的树生成算法生成邻居生成树，以AMI注入功率量测为负荷依次进行潮流计算，选择电压估计值与量测值最匹配的生成树作为最终拓扑辨识结果。文献[7]提出了一种基于AMI量测的图模型近邻估计的配电网拓扑辨识方法，先将相邻时刻AMI系统电压幅值量测之差视作高斯随机变量，建立由随机变量组成的概率图模型的精度矩阵估计模型，再采用近邻估计算法求解图模型精度矩阵，最后采用生成树算法重建出配电网拓扑。上述算法需要配置大量的量测设备，现阶段配电网还无法满足这一要求。另一类是基于数据驱动的方法。文献[8]对智能电表量测的电压曲线进行相关分析，结合电压幅值的比较，确定配电网的拓扑连接关系。文献[9]利用AMI提供的负荷量测信息和网络数据，获得同一配电变压器下的各负荷所属耦合节点电压以及所属支路电流，再通过节点电压和支路电流的相关分析，结合耦合节点电压幅值大小，确定低压配电网的拓扑结构。文献[1]利用配电馈线的数个连续的电压量测构造趋势向量，与预先构造的对应各种拓扑变化的趋势向量库进行比较，判断状态发生变化的开关，该方法只能用于检测一个开关状态的变化。文献[10]根据主成分分析的图论解析和能量守恒，通过智能电表的用能数据得到辐射状配电系统的拓扑结构。文献[11]提出了一种基于智能电表数据的配电网拓扑辨识物理概率网络模型，用概率图模型描述母线之间的连接及电压相关性，用信念传播算法推断配电网的运行状态。文献[12]提出了一种基于智能电表历史数据的中压和低压配电网拓扑生成方法，采用马尔可夫随机场MRF（Markov ran⁃dom field）算法求解节点相关性，用改进的极大似然法求解MRF模型，用迭代筛选算法实现拓扑识别。文献[8-12]均利用相关性判断节点的连接关系，认为节点越近，相关性越强。随着DG的大量接入，潮流双向流动，这一假设不一定成立，因此这些方法仅适用于辐射状配电网。文献[13]提出了核心节点映射深度网络KNDN（kernel node map deep net⁃work）用于配电网拓扑辨识，KNDN通过核节点映射将卷积神经网络的核与配电系统的物理拓扑联系起来，该方法需要人工将量测排列成卷积核，不同的配电网需要不同的量测，因此通用性不强。文献[14]采用轻量梯度提升机LightGBM（light gradient boosting machine）筛选出对配电网拓扑辨识最有效的量测特征，采用深度神经网络DNN（deep neural network）进行配电网拓扑辨识，其特征选择方法没有考虑所选特征间的相关性，会选出冗余特征，且DNN的超参数采用网格搜索确定，搜索效率较低。

针对现有方法的不足，提出了基于改进蝠鲼觅食优化IMRFO（improved manta ray foraging optimiza⁃tion）支持向量机SVM（support vector machine）的配电网拓扑辨识方法（IMRFO-SVM）。考虑到量测数据缺失的问题，提出了基于电压方差K近邻的缺失数据填补方法。针对区县农村配电网量测设备不足的问题，利用IMRFO同时进行特征选择和SVM参数的优化，筛选出对配电网拓扑辨识最有效的部分电压幅值量测。通过两个配电网算例验证了所提方法的有效性。

1 配电网拓扑辨识总体流程

1.1 总体流程

本文所建立的配电网拓扑辨识方法IMRFOSVM的总体流程如图1所示。在离线训练阶段，首先要利用SCADA系统采集不同拓扑结构下多种负荷水平的断面电压幅值量测数据和相应的拓扑标签，组成训练数据集。再对训练数据集进行归一化处理，之后用IMRFO同时进行特征选择和SVM参数的优化，筛选出对配电网拓扑辨识最有效的部分节点电压幅值量测，这些节点电压幅值量测构成最优特征子集，优化后的SVM参数可构建最优拓扑辨识模型。在在线应用时，对实时采集的断面电压幅值量测数据，先进行归一化处理，如有缺失的量测数据，则进行缺失数据的填补，再选出最优特征子集，输入SVM最优模型进行辨识，得到预测的当前拓扑结构。

图1 配电网拓扑辨识总体流程Fig.1 Overall flow chart of distribution network topology identification

1.2 训练数据集构建

配电网中的量测主要有部分节点电压幅值、支路功率和支路电流实时量测，还有许多节点注入功率伪量测。节点电压幅值量测对于配电网拓扑辨识的重要性远大于功率量测[14]，故将各节点电压幅值量测作为原始特征集。实际配电网的运行拓扑是有限的[13]，故先找出配电网的可行拓扑结构，并采集各拓扑结构在不同负荷水平和DG出力下的节点电压幅值量测，与相应的拓扑标签，构成训练数据集。

1.3 数据归一化

对配电网的某一节点，在不同的拓扑结构下，其电压幅值的变化范围较小，直接作为输入特征则拓扑辨识的效果不理想。为此对节点电压进行归一化处理，方法如下：

1.4 缺失数据填补

在采集量测数据时，可能因为量测设备或通信链路故障导致部分数据缺失，影响后续的数据分析和处理。对于缺失部分数据的训练样本，直接丢弃并重新采集数据；对含缺失值的测试样本，则对样本进行数据填补，确保能进行拓扑辨识操作。文献[14]提出了基于最小方差的缺失值填补方法。该方法基于同一拓扑结构下的节点电压曲线形状相似的特点，在训练集中找到与测试样本电压曲线差向量方差最小的样本，根据该样本估计测试样本的缺失值。该方法运算工作量较小，但对量测噪声比较敏感，因此，本文将K近邻KNN（K nearest neighbor）与该方法结合，提出了基于电压方差KNN的缺失数据填补方法。

2 基于IMRFO-SVM的配电网拓扑辨识模型

2.1 支持向量机

SVM被公认为是一种有效的数据分析和模式识别技术。与传统的统计理论不同，SVM利用Vap⁃nik-Chervonenkis维数理论和结构风险最小化原理来解决分类和回归问题。SVM的基本概念是通过最大化支持向量之间的间隔来创建一个最优的超平面。SVM可以很容易地解决线性分类问题。在非线性分类问题中，利用映射函数将原始低维数据映射到高维数据空间，将非线性不可分的分类问题转化为线性可分的分类问题。在求解过程中引入了核函数。核函数有线性函数、多项式函数、Sig⁃moid函数和高斯函数等，其中高斯核函数是最常用的，因为它只需要确定一个参数，并且对非线性问题具有很好的分类能力[15]。因此，采用的高斯核为

式中，γ表示核函数参数。

除了核函数参数，对非线性分类问题，还需要惩罚参数C用于对结构风险和经验风险进行折中。SVM的分类性能受到核函数参数γ和惩罚参数C的显著影响，因此需要对这两个参数进行优化。

2.2 改进蝠鲼觅食优化算法

蝠鲼觅食优化MRFO（manta ray foraging optimi⁃zation）算法[16]是2020年提出的一种群体智能算法，该算法模仿蝠鲼的觅食过程，对其链式觅食（chain foraging）、螺旋觅食（cyclone foraging）以及翻转觅食（somersault foraging）行为进行数学建模，对蝠鲼的个体位置进行更新，实现最优解的搜索，适用于连续参数的优化。为了同时进行特征选择和SVM参数的优化，需要对MRFO进行改进，为此构造离散化的MRFO算法IMRFO。

2.2.1 蝠鲼种群初始化

IMRFO采用二进制方式对SVM参数和特征集合进行编码。对SVM的核函数参数γ和惩罚参数C都用长度为L的二进制串进行编码。对于特征集合，每一个特征用一位二进制表示，1表示该特征被选中，0表示该特征未被选中。

设蝠鲼种群规模为Nm，第i个蝠鲼个体位置的二进制编码为：为参数γ的二进制位串；为参数C的二进制位串；为特征位串，即为hi的各维特征。对蝠鲼种群的每个个体的每一位都随机初始化为0或1。在用SVM进行拓扑辨识时，由特征位串被选中的特征构成特征子集，作为SVM的输入特征向量，并将参数γ和C的二进制位串解码成十进制数，根据式（8）转换成实际数值为

2.2.4 翻转觅食

在翻转觅食行为中，食物的位置被视为一个轴心。每只蝠鲼都倾向于绕着轴心来回游动，翻转到一个新的位置。因此，每只蝠鲼总是围绕目前为止找到的最佳位置更新自己的位置，其数学模型为

式中：G为翻转因子，决定了蝠鲼的翻转范围，此处G=2；r2和r3均为[0，1]区间均匀分布的随机数。

2.2.5 蝠鲼位置二值化

上述蝠鲼觅食行为得到的蝠鲼个体各维度新的位置都是连续的值，需要进行二值化，方式如下：

2.2.6 适应度函数

IMRFO算法的目标是在SVM的拓扑辨识准确率和选取的特征数量之间取得最佳折中。即需要在迭代过程中在选取较少特征数目的同时使得拓扑辨识准确率越高，适应度越好。IMRFO要最小化适应度函数，为此定义适应度函数为

式中：xi为蝠鲼种群中的第i个个体；acc为SVM的拓扑辨识准确率，是训练集上5折交叉验证拓扑辨识准确率的平均值；wacc为拓扑辨识准确率的权重；1-wacc为特征数量的权重。

2.3 基于IMRFO的特征选择和参数优化

IMRFO进行特征选择和SVM参数优化的流程图如图2所示。IMRFO返回的适应度最优的个体经过解码后，得到最优核函数参数γ*和惩罚参数C*，以及最优特征子集。这将用于实时采集的断面电压幅值量测数据的拓扑结构预测。

图2 IMRFO进行特征选择和SVM参数优化的流程Fig.2 Flow chart of feature selection and SVM parameter optimization by IMRFO algorithm

3 算例分析

为验证所提算法的有效性，采用IEEE 33节点配电网和PG&E 69节点配电网作为算例进行分析。各拓扑结构的所有节点的电压幅值量测数据由MATPOWER软件通过潮流计算获得[17]。

算例中的所有算法由Python语言实现，运行环境为2.5 GHz CPU、8 GB内存的笔记本电脑。为了更好地模拟配电网运行特性，光伏电站和风力发电机24 h的发电曲线采用文献[18]中的数据，并将各节点的负荷分为居民、商业和工业负荷3种类型，其24 h的负荷曲线参见文献[18]。为生成多样化的训练集和测试集样本，参考文献[14]中的方法，假设DG的出力服从高斯分布，标准差设为发电曲线实际出力的30%，负荷有功功率也满足高斯分布，标准差为负荷曲线上实际负荷的20%，负荷的功率因数服从[0.75，0.85]的均匀分布。假设风力发电机能维持机端电压恒定，将所在节点设为PV节点，光伏电站所接节点设为PQ节点。

3.1 IEEE 33节点配电网

IEEE 33节点配电网的初始拓扑结构如图3所示，该系统包含32条支路，5条联络线（虚线所示），具体线路参数参见文献[19]。在系统中接入4组DG，其中PV1和PV2表示光伏电站，WT1和WT2表示风力发电机，容量参见文献[18]。各节点的负荷类型参见文献[18]。以图3所示的拓扑结构为基础，选择57种典型拓扑作为待辨识的拓扑集合，其中包括15种网状结构，其他为辐射状结构。在每种拓扑下通过MATPOWER软件仿真生成48个样本，样本总数为2 736个。每个样本的初始特征共33维，即所有节点的电压幅值V1～V33，随机选取80%的样本（2 188个）组成训练集，其余的样本（548个）构成测试集。

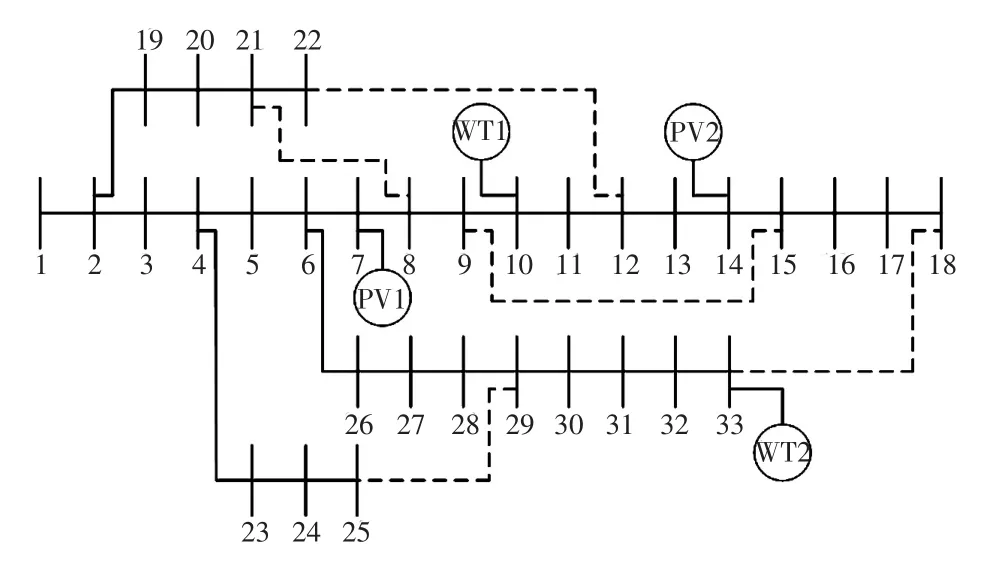
图3 IEEE 33节点配电网的初始拓扑结构Fig.3 Initial topology of IEEE 33-bus distribution network

利用IMRFO优化SVM的参数，用所有节点电压幅值构成特征向量，拓扑辨识的准确率为0.996。为了验证本文所提IMRFO-SVM算法的效果，与基于遗传算法GA（genetic algorithm）、二进制粒子群算法BPSO（binary particle swarm optimiza⁃tion）的特征选择和SVM参数联合优化算法进行比较，记为GA-SVM[20]和BPSO-SVM[21]。参数C的搜索范围为[0.1，2 000]，参数γ的搜索范围为[0.001，1]，辨识准确率权重wacc=0.8。对3种算法，设二进制串长度L=10，种群规模Nm=20，最大迭代次数M=50；对GA，交叉概率取0.8，变异概率取0.05。3种算法在测试集上的准确率和计算时间如表1所示。从表1可以看出，IMRFO-SVM取得了最高的测试集准确率，计算时间最短。本文方法找出的最优特征子集包含13个节点电压幅值，即{V7,V8,V10,，占节点总数的39.4%。只要在这些节点配置电压幅值量测，即可取得良好的拓扑辨识效果，只比采用全部节点电压幅值作为输入特征量的准确率低0.3%。

表1 3种算法的性能比较（IEEE 33节点配电网）Tab.1 Comparison of performance among three algorithms（IEEE 33-bus distribution network）

3.2 PG&E 69节点配电网

PG&E 69节点配电网的初始拓扑结构如图4所示，该系统包含68条支路，5条联络线（虚线所示），具体线路参数参见文献[22]。在系统中接入5组DG，其中PV1、PV2和PV3表示光伏电站，WT1和WT2表示风力发电机，容量参见文献[23]。除了中间节点，其他节点的负荷类型如表2所示。

图4 PG&E 69节点配电网的初始拓扑结构Fig.4 Initial topology of PG&E 69-bus distribution network

表2 PG&E 69节点配电网的负荷类型Tab.2 Load types of PG&E 69-bus distribution network

以图4所示的拓扑结构为基础，选择46种典型拓扑作为待辨识的拓扑集合，其中包括15种网状结构，其他为辐射状结构。在每种拓扑下通过MATPOWER软件仿真生成48个样本，样本总数为2 208个。每个样本的初始特征共69维，即所有节点的电压幅值V1～V69，随机选取80%的样本（1 766个）组成训练集，其余的样本（442个）构成测试集。

利用IMRFO优化SVM的参数，用所有节点电压幅值构成特征向量，拓扑辨识的准确率为0.980。3种算法的参数设置与IEEE 33节点配电网相同，其拓扑识别的性能如表3所示。

表3 3种算法的性能比较（PG&E 69节点配电网）Tab.3 Comparison of performance among three algorithms（PG&E 69-bus distribution network）

从表3可知，本文方法（IMRFO-SVM）取得了最高的测试集准确率，且计算时间最短，只比采用全部节点电压幅值作为输入特征量的准确率低0.5%。本文方法找出的最优特征子集包含30个节点电压幅值，即{V3,V5,V9,V10,V13,V16,V19,V19,V20,V22,V24,V25,V27,V28,V32,V34,V36,V38,V39,V43,V45,V48,V49,V50,V51,V53,

}V55,V65,V66,V67,V68，占节点总数的43.5%。

3.3 算法的适应性分析

3.3.1 对量测噪声的适应性

为了验证本文算法对测量误差的鲁棒性，在训练集和测试集的节点电压幅值量测数据中添加零均值的高斯随机噪声N(0,σ)，σ为标准差，设置为节点电压幅值的0.01%和0.05%。本文算法添加不同量测噪声时对IEEE 33节点配电网和PG&E 69节点配电网的拓扑辨识精度如表4所示。从该表可以看出，存在量测噪声时，本文方法仍具有较好的适应性，具有较高的拓扑辨识精度。

表4 不同量测噪声下的拓扑辨识精度Tab.4 Accuracy of topology identification under different measurement noises

3.3.2 对量测缺失的适应性

对测试集中的每一个样本，随机删除某一个节点电压幅值量测，并用本文的电压方差KNN方法、文献[14]的最小方差方法以及KNN方法进行缺失数据填补（近邻个数K=4），将处理后的测试集用IMRFO-SVM进行拓扑辨识。为了验证本文方法对量测噪声的鲁棒性，在训练集和测试集的节点电压幅值量测数据中添加零均值的高斯随机噪声，辨识精度如表5和表6所示。从结果可以看出，存在量测噪声时，本文的填补方法要优于其他方法，量测噪声增大时，本文方法的优势更为明显，即本文的缺失值填补方法对量测数据缺失具有较好的适应性，能较准确地估计缺失量测值。

表5 3种填补方法的性能比较（IEEE 33节点配电网）Tab.5 Comparison of performance among three imputation methods（IEEE 33-bus distribution network）

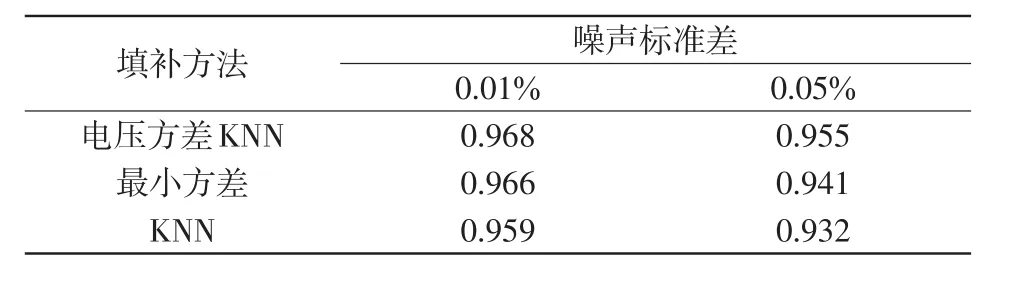
表6 3种填补方法的性能比较（PG&E 69节点配电网）Tab.6 Comparison of performance among three imputation methods（PG&E 69-bus distribution network）

4 结语

提出了一种基于改进蝠鲼觅食优化支持向量机的配电网拓扑辨识方法。利用改进蝠鲼觅食算法同时进行特征选择和支持向量机参数的优化，筛选出对配电网拓扑辨识最有效的部分电压幅值量测。通过IEEE 33节点配电网和PG&E 69节点配电网验证了该方法的有效性。所提方法仅需一个时间断面的部分电压幅值量测数据，适用于量测不足的区县农村配电网，计算速度可满足实时的拓扑辨识。另外，提出了基于电压方差K近邻的量测缺失数据填补方法，能够较准确的估计测试样本的缺失特征。下一步的工作是研究支持向量机的增量学习算法，以对未知拓扑进行辨识。