基于CFD的三体船侧体布局优化

田高辉， 冯佰威*， 常海超

(武汉理工大学 a.高性能船舶技术教育部重点实验室；b.交通学院，湖北 武汉 430063)

0 引 言

三体船作为一种高性能船舶，凭借其良好的快速性、耐波性、隐身性等诸多单体船不具备的特点，近年来在军用和民用领域均得到广泛的关注。目前，国内外的研究表明，在实际航行中，三体船的主体与侧体之间的兴波干扰复杂，对总阻力有较大的影响。如果侧体相对于主体的横向位置和纵向位置布置得当，有可能大幅减小兴波阻力，进而减小总阻力。

目前，国内外对三体船侧体布局优化的研究、模型试验和数值模拟大多采用枚举法。枚举法虽可得到不同侧体布局下阻力性能的变化规律，但无法确定某航速下最优的侧体布局。PALMER等[1]结合一种改进的粒子群优化算法对三体船侧体位置进行优化，探讨阻力最小时所对应的侧体位置。MYNARD[2]采用三维 Rankine 源面元法系统地研究侧体位置对三体船兴波阻力的影响，同时优化结果显示侧体位置会随着速度变化而发生较大改变。JAVANMARIDI等[3]对三体船的阻力性能进行研究，共选取侧体的2个横向位置和4个纵向位置，通过自行编制的计算流体动力学(Computational Fluid Dynamics,CFD)程序，计算并分析不同侧体位置对三体船阻力性能的影响。郦云等[4]对高速三体船模在弗劳德数Fr为0.1～0.8时3个横向间距、5个纵向间距共15个状态进行阻力试验，并根据模型试验结果分析横向间距和纵向间距对兴波阻力系数的影响。邓小敏等[5]基于势流理论，应用Kelvin源格林函数结合边界元方法，计算Wigley船型的三体船在定常移动情况下的兴波阻力，通过改变航速，侧体与主体间的纵向、横向间距，计算分析三体船兴波阻力随航速、侧体布局间的关系曲线，得到航速一定时较优的侧体布局。周广利等[6]采用CFD软件STAR-CCM+模拟三体船周围黏性流场，对三体船模进行数值计算，求出侧体与主体间的兴波干扰值，得到较佳的布局方案。

在此基础上，以某高速三体船为例，利用SHIPMDO-WUT软件平台，将 CFD技术与粒子群算法相结合。对三体船侧体布局进行优化，得出4种不同弗劳德数下阻力性能最优的三体船侧体布局方案。最后，将优化船与母型船的总阻力进行比较，以验证该方法的可行性与有效性。

1 基于CFD的阻力数值计算

从减小船体兴波阻力的角度出发，对三体船侧体布局进行优化，用到的CFD软件为SHIPFLOW和STAR-CCM+，其中：SHIPFLOW用于计算三体船的兴波阻力及船型优化；STAR-CCM+用于计算最优三体船的总阻力并与试验结果进行对比验证，以保证优化结果的准确性。

1.1 三体船的几何描述

三体船计算模型由1个主体和2个侧体组成，两者均为圆舭船型，2个侧体在主体的左右两侧对称摆放，排水量为总排水量的7%。实船与船模的缩尺比α=15。模型的主尺度参数如表1所示，三维模型如图1所示。

表1 三体船模型主尺度参数

图1 母型船三维模型

1.2 三体船总阻力的数值计算

(1)总阻力计算原理

采用STAR-CCM+计算总阻力需要满足由质量守恒转化得到的连续性方程和由动量守恒转化得到的N-S方程；离散化方法采用有限体积法；湍流模型选用剪切应力传输(Shear Stress Transfer，SST)k-ω湍流模型，可较好地处理近壁面问题和逆压分离流问题，是目前船舶CFD计算中应用较为广泛的模型；船体周围的自由液面模拟采用流体体积(Volume of Fluid，VOF)函数法。通过动态流体相互作用(Dynamic Fluid Body Interaction，DFBI)中的旋转与平移模块求解三体船的纵倾和升沉问题。

(2)设置计算域与边界条件

计算域取为长方体，大小为42.40 m×25.32 m×12.66 m(长×宽×高)，即在纵向上自艏部向前延伸1倍的船长，自艉部向后延伸3倍的船长；横向上自中纵剖面向左右各延伸1.5倍的船长；垂向上自船底向下延伸1倍的船长，向上延伸0.5倍的船长。边界条件的设定：三体船表面设为壁面边界条件；艏部前方、顶部和底部设为速度入口边界条件；艉部后方设为压力出口边界条件；两侧设为对称边界条件。如图2所示。

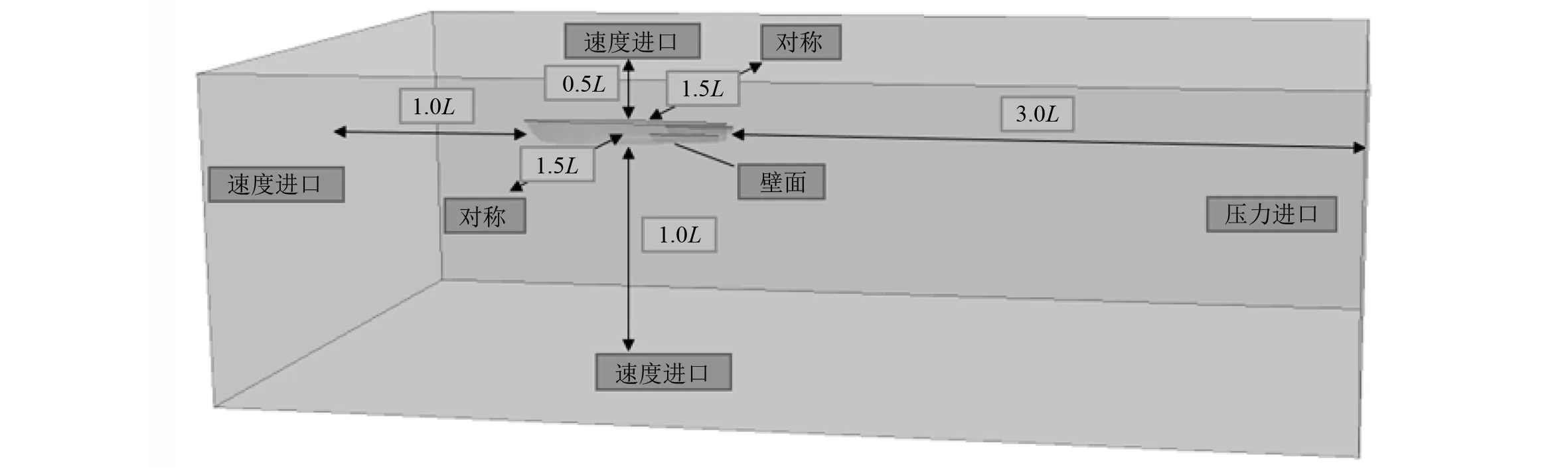
图2 三体船计算域与边界条件

(3) 网格划分

计算域网格分为重叠区域网格和背景区域网格。对于重叠区域网格，除了需要对船体表面和船体周围的网格进行加密外，还需要对自由液面附近的网格进行加密；对于背景区域网格，除了对自由液面附近的网格进行加密外，还需要对重叠网格对应的背景网格加密区域进行相应的网格加密，使重叠网格的网格尺寸满足相应的尺寸要求。前期进行大量计算确定相应的网格尺寸，图3为网格的划分情况，表2为各加密区的网格划分尺寸，其中：重叠网格区域的网格数量为131万，背景区域的网格数量为96万，总网格数量为227万。

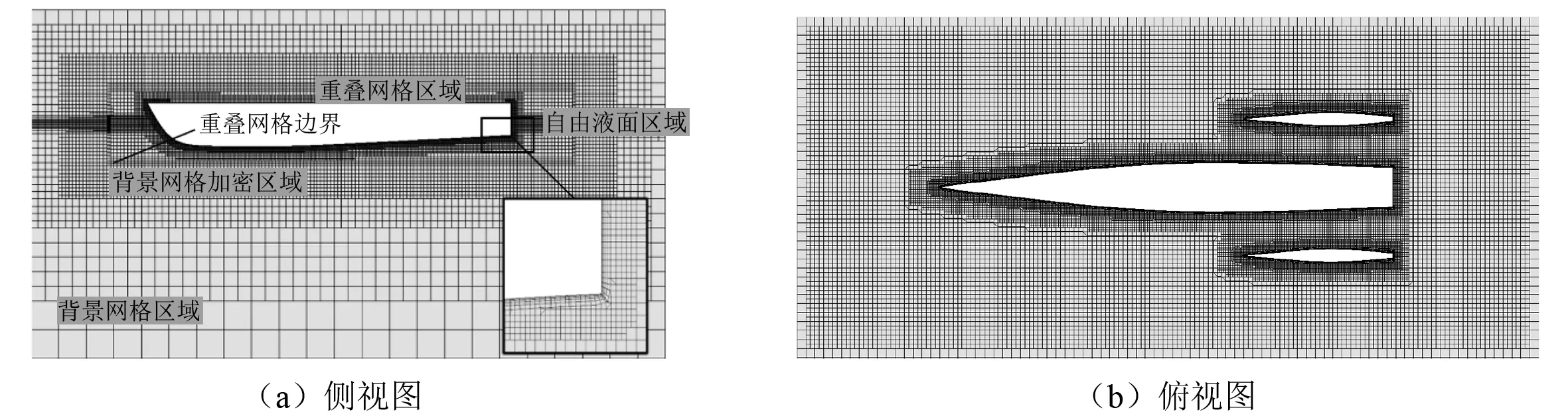
图3 计算域网格划分

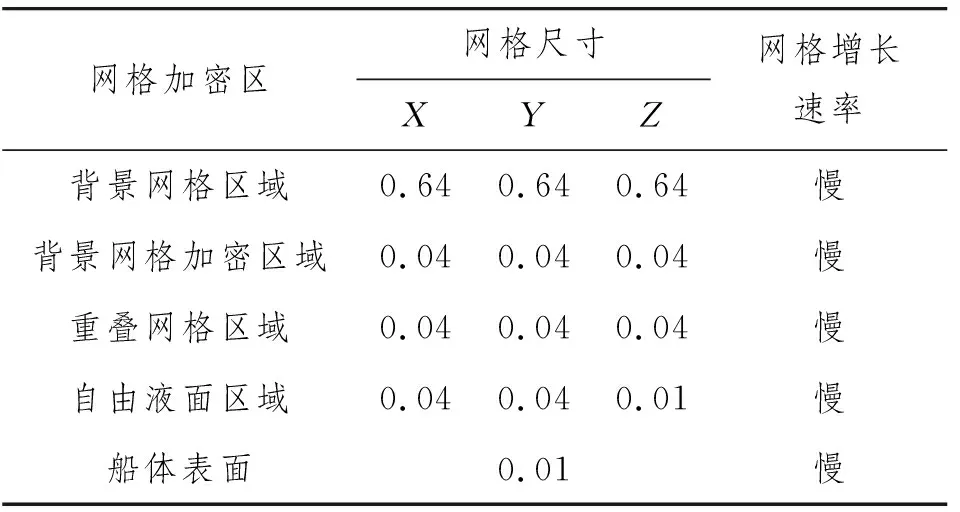
表2 各加密区网格划分尺寸 m

1.3 数值计算结果与试验验证

分别计算不同弗劳德数下母型船的总阻力，与船模试验结果进行对比，计算结果如表3所示，对比如图4所示。模型试验在中国航空工业第六〇五研究所拖曳水池完成。该水池的主要参数：池长为500.0 m，池宽为6.5 m，水深为5.0 m。拖车速度为0～25 m/s，精度为0.1%。船模阻力Rt由电测式阻力仪测得，阻力仪安装在拖车上，拖线经导轮与阻力仪连接。下端连接拖线带动船模前进。在试验中，船模的纵、横摇与升沉运动不受约束，拖点设在模型的重心处。在整个试验过程中，保持模型的总排水量不变。测得试验水池的平均水温为17 ℃。船模试验现场如图5所示。

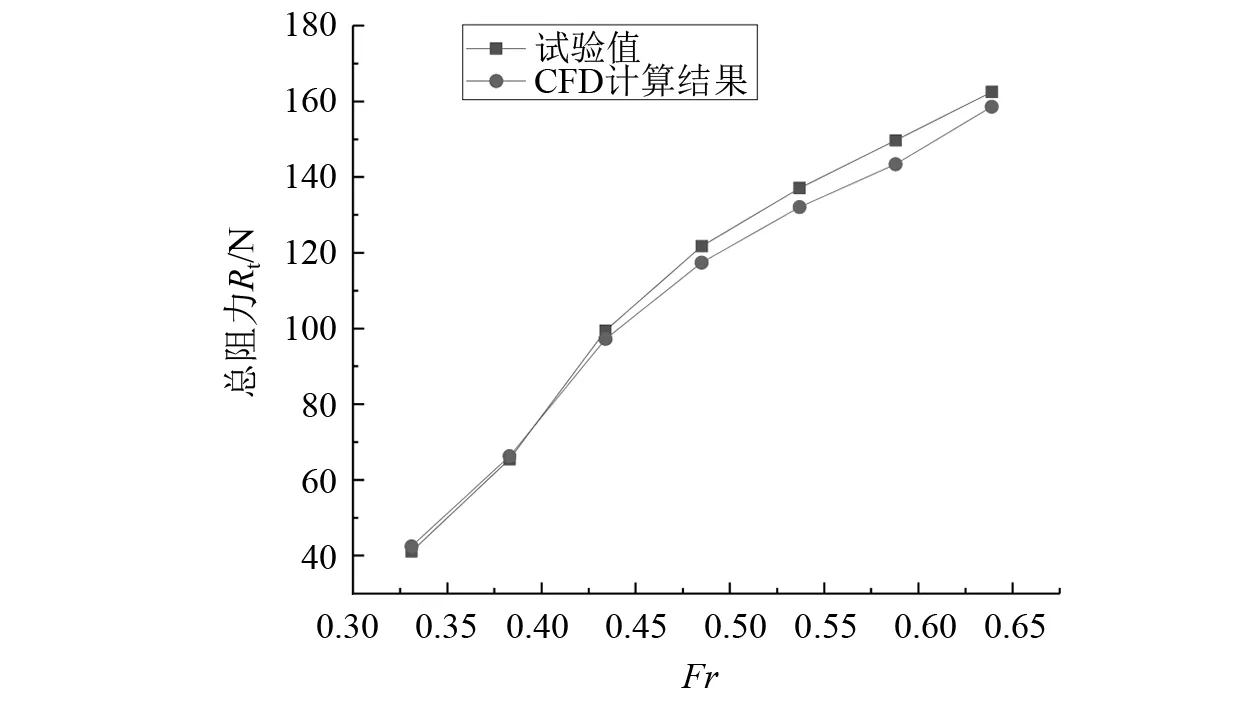
图4 阻力计算结果与试验值比较

图5 三体船试验图

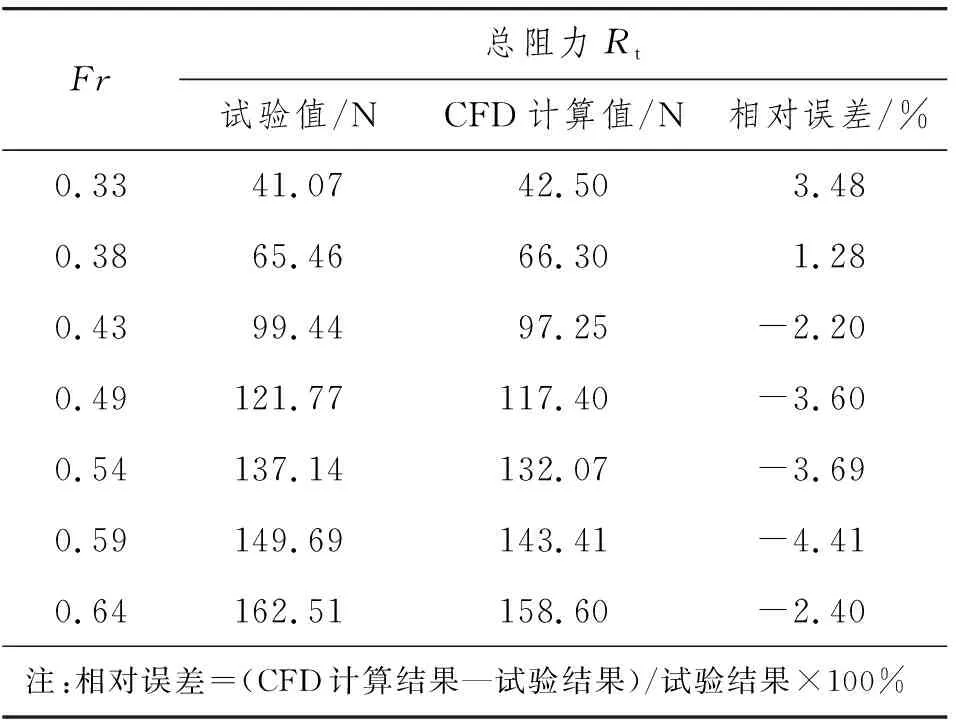
表3 总阻力对比

对比结果可看出：不同弗劳德数下的阻力计算值均与试验结果吻合良好，最大误差不超过5%。说明所采用的阻力数值计算方法精度比较可靠。总阻力Rt的CFD计算值可对三体船的阻力性能进行准确的预报。

2 三体船侧体布局优化

2.1 优化问题描述

以第1.1节的高速三体船为例，选取侧体的横向位置和纵向位置为优化变量，以4个不同弗劳德数下的兴波阻力系数为优化目标进行优化。再对优化船与母型船的总阻力进行验证，探讨侧体布局变化对三体船兴波阻力及总阻力性能的影响。

三体船的侧体布局主要包括横向位置和纵向位置。两者均可使主体和侧体产生兴波干扰。侧体与主体之间的横向位置关系用y表示，代表主体纵向中心线与侧体纵向中心线之间的距离；侧体与主体之间的纵向位置关系用x表示，代表主体艉部与侧体艉部之间的距离，具体关系如图6所示。母型船的侧体纵向位置x=1.36 m，位于主体的舯部，横向相对位置y=1.02 m。

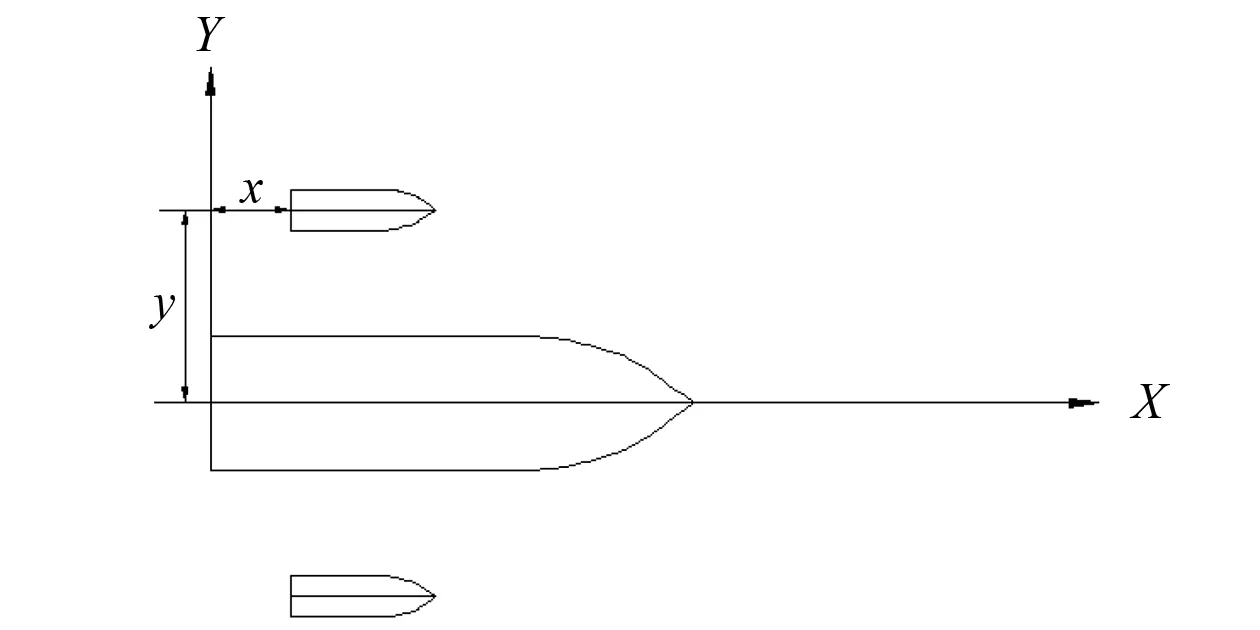
图6 三体船主体与测体位置关系

2.2 数学模型建立

取4个不同弗劳德数Fr=0.331,0.434,0.537, 0.639的兴波阻力系数为优化目标，定义如下：

min(fobj)=Cw

(1)

式中：fobj为目标函数；Cw为兴波阻力系数。

设计变量为侧体纵向相对位置x和横向相对位置y，则变量上下限表示为

(2)

式中：xmin、xmax、ymin、ymax分别为侧体纵向相对位置和横向相对位置的最小值和最大值。侧体纵向位置不超过主体的艏部和艉部，则xmin=0 m，xmax=2.72 m。侧体的横向相对位置过小会引起流动阻塞效应，且甲板面积会变小，影响上层建筑的布置；横向相对位置过大无法产生有力的干扰，连接桥的结构也无法保证。根据文献[7]的研究取1～5倍船宽，则ymin=0.45 m，ymax=2.25 m。

2.3 优化流程

基于开发的SHIPMDO-WUT软件平台，通过编制程序实现侧体布局变换与SHIPFLOW软件输入数据间的自动连接，利用SHIPFLOW软件计算其目标函数值，再结合粒子群算法完成从全局探索到局部空间寻优的整个优化流程。将优化前后的三体船兴波阻力系数与总阻力进行比较, 以验证该方法的可行性与有效性。其优化流程如图7所示。

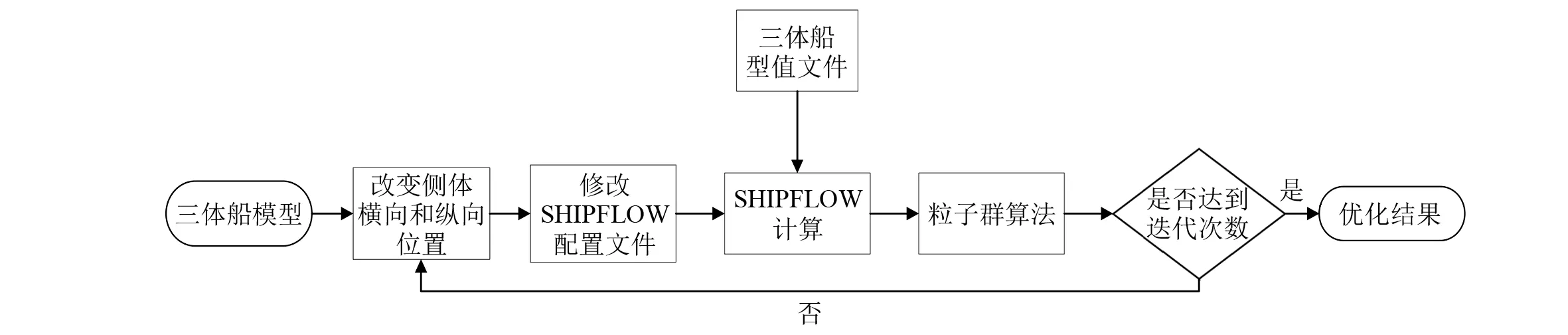
图7 优化流程

优化流程简述如下：

(1)通过优化算法，调整优化变量，实现对母型船侧体横向相对位置和纵向相对位置的自动修改。

(2)生成SHIPFLOW 所需要的新船型配置文件和型值文件，并计算船体兴波阻力。

(3)以兴波阻力系数最小为优化目标，选择粒子群优化算法，种群数取20，粒子数取30，进行三体船侧体布局的优化。

(4)若达到迭代次数，则输出最优解集，反之，返回至初始流程，重新进行优化。

2.4 优化结果分析

经过630次迭代计算，收敛过程如图8所示，将获得的优化船结果与母型船对比，计算结果如表4所示。

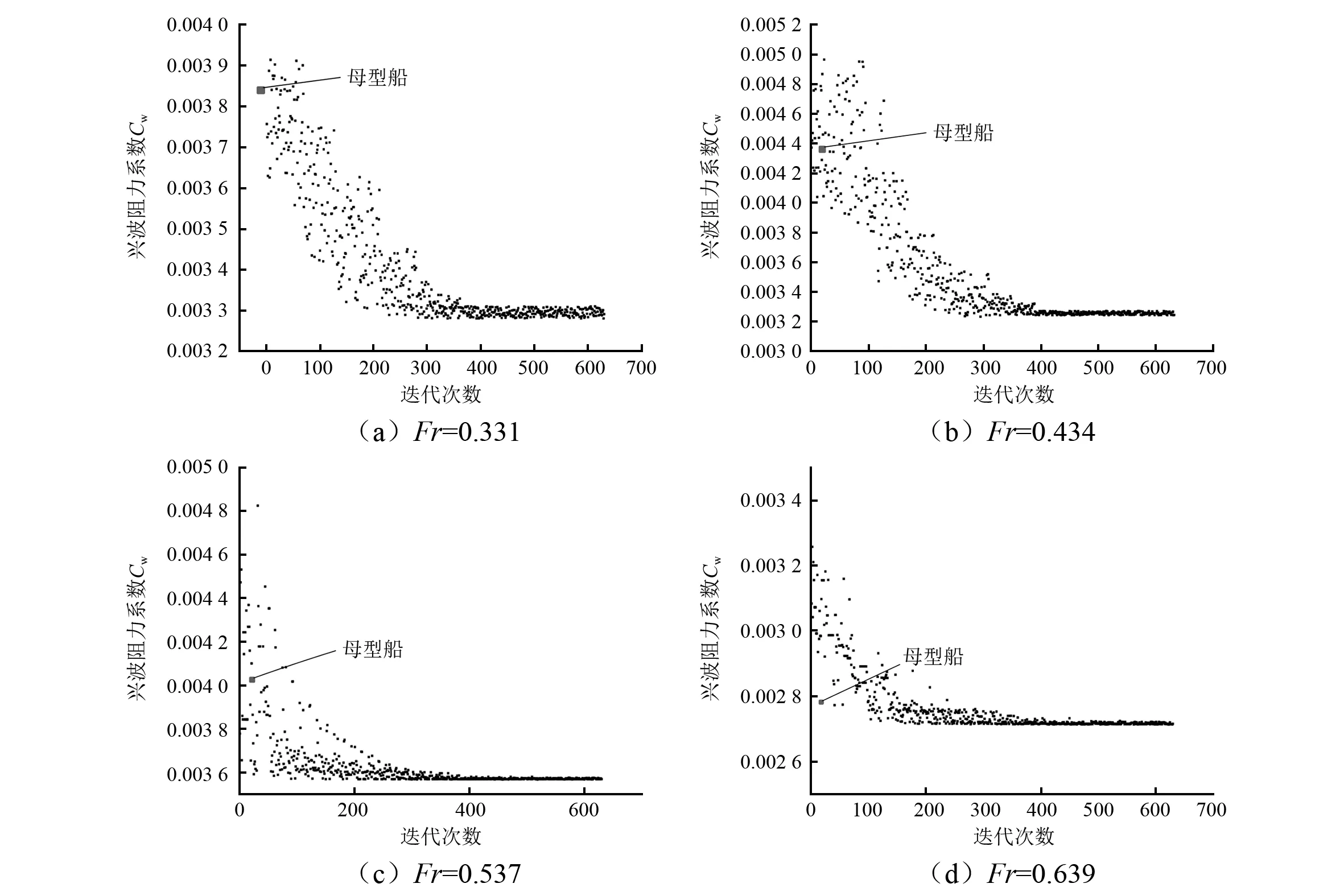
图8 取不同弗劳德数Fr的优化收敛过程

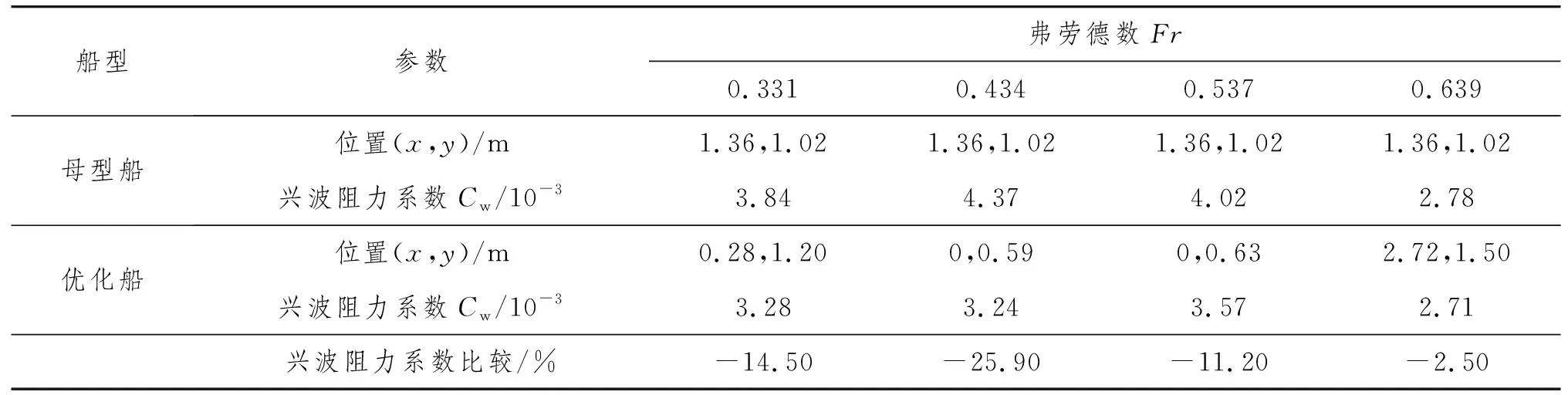
表4 取不同弗劳德数Fr的优化船与母型船计算结果对比

表4列出母型船和优化船的位置及兴波阻力系数的变化值。由表4可知：与母型船相比，当Fr=0.331时，优化船纵向相对位置为0.28 m，横向相对位置为1.20 m，侧体位于主体的舯后位置，兴波阻力系数下降14.50%；当Fr=0.434和0.537时，优化船的侧体均位于主体的艉部，且横向相对位置较小，兴波阻力系数分别下降25.90%和11.20%；当Fr=0.639时，优化船的侧体位于主体的艏部位置，兴波阻力系数下降2.50%。由于优化前后船体湿表面积变化很小，因此，近似认为阻力变化和阻力系数变化幅度同步。对比文献[8]和文献[9]的试验结果，符合不同弗劳德数下阻力性能较优时侧体布局的分布规律。

为进一步验证结果的可靠性，用STAR-CCM分别计算4种弗劳德数下母型船和优化船的总阻力，计算原理参考文献[10]，结果对比如表5所示。

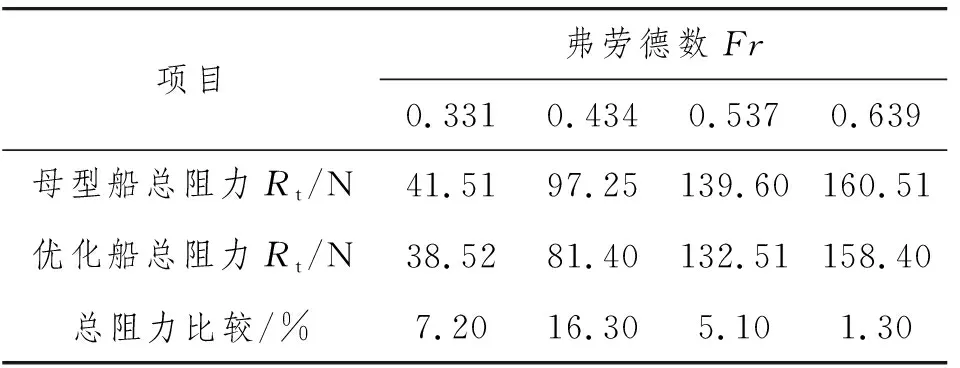
表5 取不同弗劳德数Fr的优化船与母型船总阻力对比

由表5可知：在不同弗劳德数下，优化船较母型船的总阻力均有不同程度的下降；总阻力下降的趋势与兴波阻力一致。由于在中高速时，兴波阻力占三体船总阻力的大部分，且黏性阻力和摩擦阻力的变化不是太大，因此减小兴波阻力，则直接减小总阻力。总阻力性能得到改善，证明三体船侧体布局的自动优化取得成功。

母型船与优化船的波形图和波切图如图9所示。由图9的波形图可看出：与母型船相比，优化船的兴波波形数量有所减少，且波形变得更加简单。由图9的波切图可看出：与母型船相比，优化船兴波的波峰和波谷均有所减小，说明侧体位置的优化对三体船船体的兴波产生显著的干扰，降低三体船的兴波阻力，进而减小总阻力。

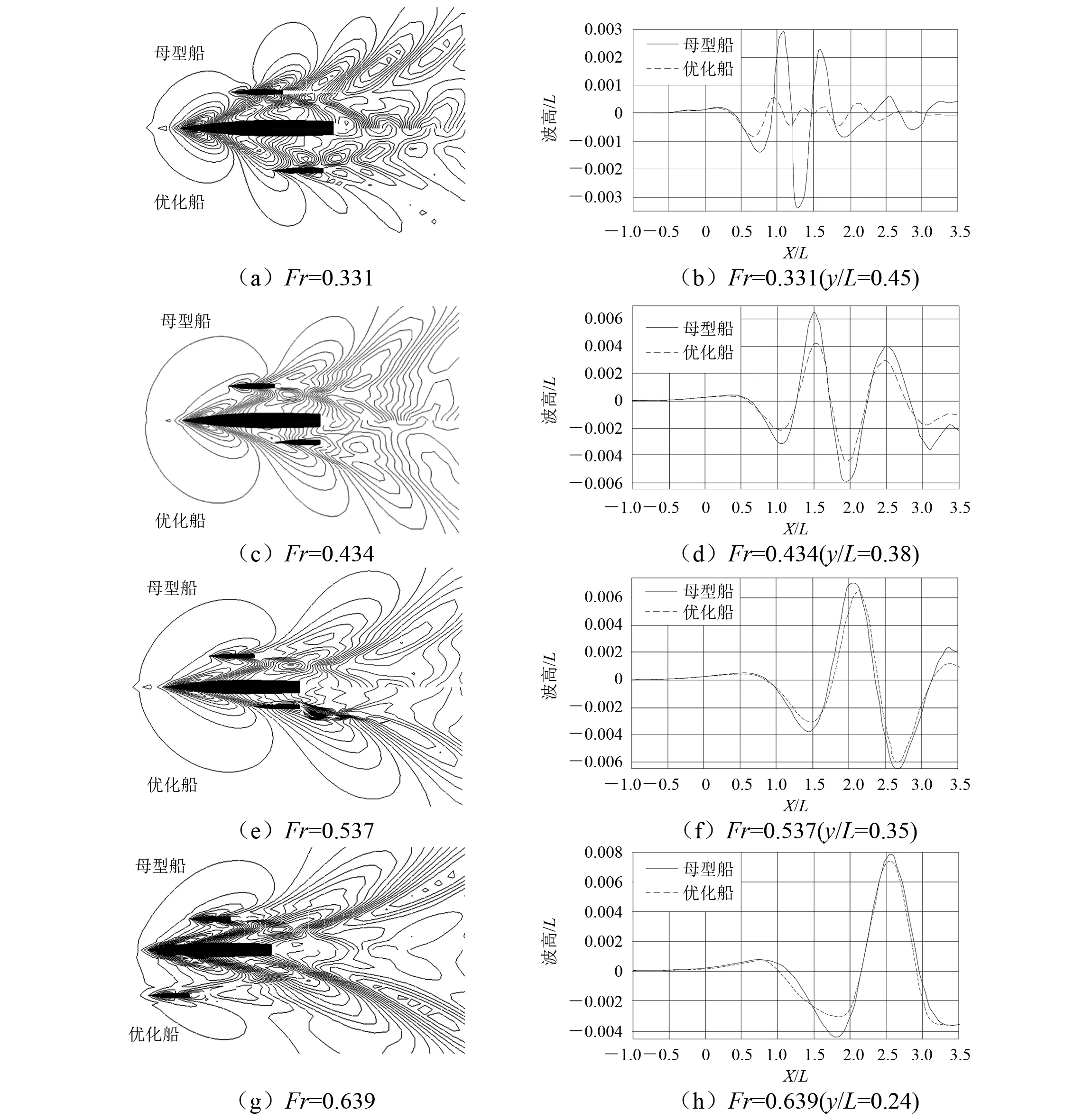
注：L为船长图9 不同Fr对应的波形图与波切图

3 结 论

以某高速三体船为研究对象，基于开发的SHIPMDO-WUT软件平台，通过编写程序，实现侧体布局的自动变化，再结合粒子群优化算法，完成三体船侧体布局优化。优化结果表明，在4个不同弗劳德数下，优化船较母型船的兴波阻力均有所下降，总阻力也相应减小，最后分别得出在4个不同弗劳德数下，总阻力性能最优的三体船侧体布局方案。

在针对三体船优化时，仅把阻力性能作为优化的目标，但在实际过程中，耐波性能也很重要，将来可针对三体船的阻力和耐波性进行多目标优化。优化后的船型未进行船模试验，但由母型船试验结果比较可知：CFD的阻力数值计算方法精度可靠，可对优化船的阻力性能进行准确的预报。研究结果可为实际生产中的三体船减阻优化设计提供参考依据。