复杂条件下格宾网箱生态护坡稳定性分析

王希萌， 张志红， 白顺果

(1.北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124； 2.河北农业大学 城乡建设学院， 河北 保定 071001)

1 研究背景

2022年冬季奥林匹克运动会将会促进我国基础设施建设的进一步发展，其众多奥运场馆的修建，不可避免地要对山体进行切削，导致原有的植被覆盖层被破坏，造成生态系统失衡，形成大量裸露边坡。秉承“绿色、共享、开放、廉洁”的办奥理念，为保护赛区生态环境，推进绿色场馆建设，急需探索一种适宜的生态护坡结构形式。格宾结构以其适用于冬季严寒气候、可快速恢复边坡生态以及能够就地取材充分利用当地切削岩土体的优势应运而生。

格宾结构(gabion)，又称石笼结构，是由机械编织而成的双绞合六边形金属网片拼接而成的箱体，或垫体内部填充符合粒径要求的块石所构成的柔性结构[1]。众多学者对格宾结构开展了试验研究、数值模拟和理论分析[2-6]。国内于2005年底引进格宾护坡技术后，在北京、湖南、湖北、重庆等地完成了多个项目，取得了良好的工程效果，工程中对格宾结构也进行了一定的研究[7]。李昀等[8-9]对格宾加筋挡墙与绿色格宾加筋挡墙的力学行为及动力特性进行了系统研究，分析了加筋格宾挡墙的土压力、挡墙变形、筋材拉应力等特征参数的分布规律，研究了其在地震作用下的变形特征及抗震机制，揭示了其在地震作用下的破坏特征。陈亮等[10]总结提出了多级台阶式格宾高挡墙路基防护新技术，具体阐述了相关的工作原理、施工工艺流程以及质量控制措施等。程林林[11]提出了一种既能满足加筋格宾挡土墙稳定性要求又能获得良好经济效果的加筋格宾挡土墙的设计方案。黄向京等[12]依托湖南某高速公路的国内首座加筋格宾组合式挡土墙工程实例，提出了该组合结构的稳定性验算方法与公式。杨涛[13]针对雷诺护垫自身抗滑稳定性能及雷诺护垫防护边坡整体稳定性进行了较系统的研究，推导了雷诺护垫自身抗滑移稳定安全系数的计算公式，并以实际工程为依托计算了铺设雷诺护垫后边坡整体稳定安全系数及自身抗滑稳定安全系数。目前在格宾支护结构的力学性能和施工工艺的研究相对成熟，但对格宾护坡的稳定性缺乏系统研究，可供参考的资料也相对匮乏[14]。格宾护坡结构作为施加在边坡表面的荷载会给边坡整体稳定性带来不利影响，且在重力、地震、降雨等作用下该结构可能沿边坡表面发生滑动导致护坡失效。因此为了推广格宾生态护坡在工程中的应用，亟需开展格宾防护边坡的稳定性研究。

在2022年冬奥会国家跳台滑雪场高切坡工程中，采用了一种新型倒梯形格宾网箱生态护坡结构形式，网箱下部填充碎石，上部铺设种植土，种植植被形成坡面绿化，以实现工程结构与生态景观的和谐统一。目前在此新型支护结构的网箱内部填充物结构性能[15]、覆绿性能[16]与受力变形性能[17]等方面均取得了一定的研究成果，但尚缺乏对于支护结构体系稳定性方面的研究。本文在此基础上，开展在地震、降雨及地震与降雨共同作用的复杂条件下格宾网箱支护边坡的整体稳定性及格宾支护结构自身稳定性研究，以探究格宾网箱生态护坡的有效性和可行性。采用MIDAS/GTS NX有限元软件，基于有限元强度折减法对格宾网箱支护边坡整体稳定性开展数值分析。基于极限平衡原理推导了格宾网箱护坡结构的自身抗滑移稳定系数计算公式，并对其自身稳定性进行分析评价，以期为类似高山滑雪赛道工程的生态护坡建设提供参考。

2 工程概况

工程场地位于河北省张家口市崇礼区枯杨树村，距崇礼城区20 km左右，为2022年冬奥会主要比赛场地之一，简称崇礼赛区。崇礼赛区拟建的国家跳台滑雪比赛场效果图及施工现场见图1。比赛场地包括出发区、结束区、比赛滑道、裁判塔和索道，其中比赛跳台斜坡地面标高为1 640～1 770 m，高差约为130 m，坡度为20°～40°。由于修建跳台滑雪场，需对山体进行削坡处理，其中位于跳台滑雪场出发区后侧的边坡区域(图1(b)中框线区域)分为I区和Ⅱ区，I区垂直放坡至放坡坡率1∶1，采用预应力锚索格构梁支护方案，以满足边坡稳定性要求，Ⅱ区放坡坡率为1∶1.5，考虑到削坡导致边坡岩土体裸露，不易于生态恢复，且切削下的岩土体的运输会增加成本，为快速恢复生态的同时又能就地取材充分利用切削下的岩土体，对此区域采用格宾网箱生态护坡方案。

图1 2022年冬奥会崇礼赛区国家跳台滑雪比赛场

3 格宾网箱生态护坡稳定性分析

3.1 边坡计算剖面选取

根据实际地形、坡体结构特征和工程地质条件，选取最具代表性剖面作为边坡计算剖面，具体详见图2。该边坡对应地面标高1 750～1 792 m，为永久性边坡，安全等级为一级。边坡总高度为42.0 m，天然边坡经开挖共形成四级边坡，其中第一级边坡垂直开挖，高度为9.6 m，顶部平台宽2.0 m；第二级边坡坡率为1∶1，坡高11.4 m，坡顶平台宽20.0 m；第三级边坡坡率为1∶1.5，坡高10.0 m，坡顶平台宽3.0 m；第四级边坡坡率为1∶1.5，坡高10.0 m。

图2 边坡计算剖面图

3.2 支护方案

对第一、二级边坡采用预应力锚索格构梁进行加固，对第三、四级边坡采用格宾网箱护坡，具体支护方案如图3所示。锚索共设8排，锚索钻孔直径为130 mm，倾角均为15°，水平间距为2.5 m，将8排锚索由上至下编号为1#～8#，1#锚索预应力为150 kN，2#锚索预应力为200 kN，其余锚索为250 kN。边坡表面采用截面尺寸为0.4 m×0.4 m、水平间距为2.5 m的方形格构梁加固，浇筑C30混凝土。第三、四级边坡坡率为1∶1.5，为使格宾网箱更好地贴合坡面，在常规的立方体网箱基础上进行改进，设计网箱贴合边坡一侧为与边坡坡率相同的倾斜面，格宾网箱示意图如图4所示。格宾网箱采用交错叠摞摆放形式，从第三级边坡坡底开始逐层向坡内缩进0.3 m摆放，各网箱间通过绞合钢丝连接，第三、四级边坡之间设有3 m宽平台，每级边坡高10 m，故每级边坡分别铺设10层网箱。在网箱放置前，对边坡进行二次切削，以留出格宾网箱放置平台。用C30的混凝土对网箱底部进行基础浇筑，基础尺寸为1.0 m×1.0 m×0.5 m。

图3 预应力锚索格构梁及格宾网箱护坡横断面布置图

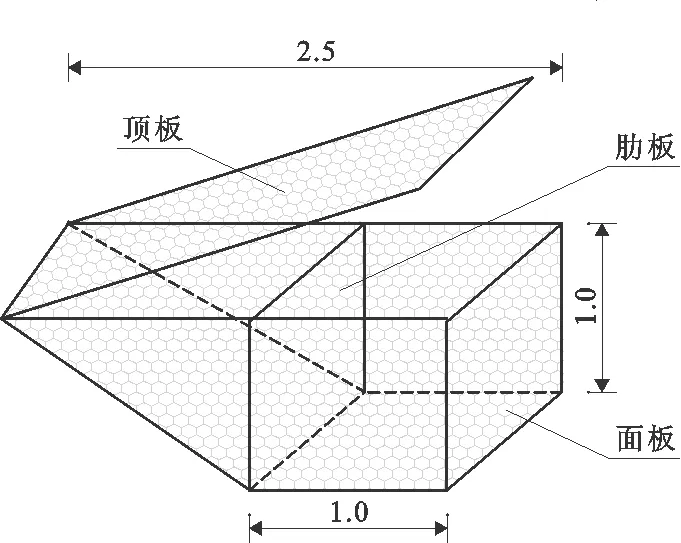
图4 格宾网箱单元示意图(单位：m)

3.3 模型建立

本文应用MIDAS/GTS NX软件进行有限元模型的建立与计算。对坡面重点区域进行网格的细化，其他区域适度控制网格密度。模型尺寸在x、y方向分别为127.0、62.3 m，上部为自由边界，左、右两侧水平约束，底部固定。 预应力锚索采用软件自带的“锚建助手”功能实现建立。混凝土格构梁是通过软件中“析取单元”功能，在岩土体2D平面网格划分完成后选择格构梁所在节点位置析取1D单元实现建立。格宾网箱模型首先建立格宾填料网格，然后采用软件中“析取”功能点选格宾填料网格边框以实现格宾网的建立，为了模拟格宾网箱之间以及格宾网箱与坡面土体之间的相互作用和接触特性，引入了界面单元的概念，采用弹塑性模型描述界面性质，建立可能会发生滑动或分离的界面。界面单元的摩擦系数Rinter反映了两者相互作用的程度。在本文中，取Rinter=0.6[18]，格宾网箱护坡有限元模型网格划分如图5所示。

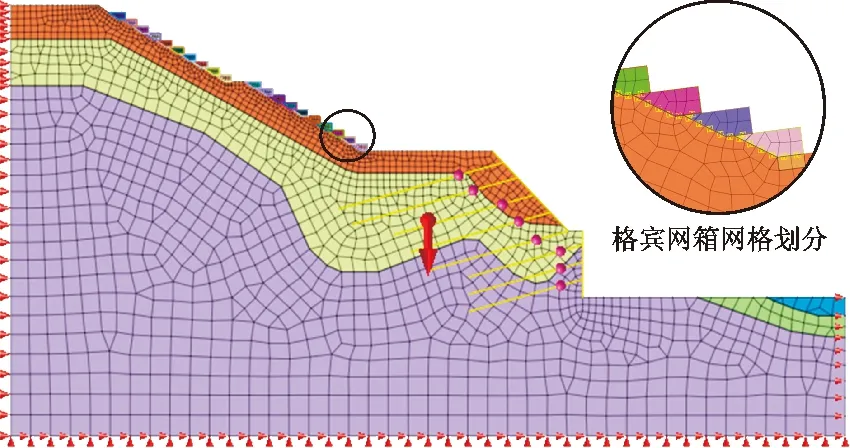
图5 格宾网箱护坡有限元模型网格划分

3.4 参数选取

场区内广泛分布地层为花岗岩(全风化)⑤11层，花岗岩(强风化)⑤12层及花岗岩(中风化)⑤13层。岩土体采用平面应变单元模拟，本构关系采用理想弹塑性模型，屈服准则为Mohr-Coulomb屈服准则。不考虑格宾填料之间的空隙，将其视为连续介质[19]。将格宾网与填料分开模拟，格宾填料本构模型为Mohr-Coulomb模型，格宾网用线弹性单元模拟。根据《北京2022年冬奥会张家口赛区古杨树场馆群(跳台滑雪比赛场)岩土工程勘察报告》和文献[14]的参数取值，并结合《岩石力学参数手册》进行工程类比，确定的边坡岩土体及支护结构的物理力学参数如表1所示。

表1 边坡岩土体及支护结构的物理力学参数

格宾网箱与坡面之间的界面参数通过软件中的属性助手按相邻单元的属性自动计算，格宾网箱之间的界面参数根据文献[20]选取，界面参数如表2所示。

表2 格宾网箱之间及其与坡面之间的界面参数

3.5 数值模拟结果及分析

边坡稳定性依据《建筑边坡工程技术规范》(GB 50330—2013)[21]进行评价。本文边坡为一级安全等级的永久边坡，在一般工况下稳定性系数Fst=1.35，地震工况下Fst=1.15。计算求得各施工阶段边坡稳定性系数及稳定性评价结果见表3。

表3中评价结果表明，未支护时边坡处于基本稳定的状态，应及时采取支护措施以保证边坡的安全稳定。未支护条件下，边坡最大剪切应变云图如图6所示。

表3 各施工阶段边坡稳定性系数及稳定性评价结果

图6 未支护时边坡最大剪切应变云图

由图6可见，边坡潜在滑动面最终位于全风化与强风化花岗岩界面处，滑动面由第二级边坡坡顶至坡脚基本贯通，边坡有可能沿界面发生浅层滑动。又考虑到第一级边坡垂直开挖，可能出现岩土体崩落现象，故在第一、二级边坡处采取支护措施。

在第一、二级边坡处经预应力锚索格构梁支护后边坡最大剪切应变云图如图7所示。由图7可见，预应力锚索格构梁支护对滑动面的发展起到了限制作用，原来位于第二级边坡处的潜在滑动面消失， 最终滑动面产生于第四级边坡坡顶至第三级边坡坡底处。经预应力锚索格构梁支护后，边坡稳定性系数Fs由未支护的1.28增大至1.55，大于规范要求的Fst=1.35，表明此时边坡已处于稳定状态。

格宾网箱护坡后边坡最大剪切应变云图如图8所示。由图8可见，格宾网箱支护后边坡潜在滑动面位置未发生改变，最大应变产生于底层格宾网箱前端，由于格宾网箱的放置使最大应变有所增大。经计算求得,第三、四级边坡再次削坡处理后稳定性系数Fs=1.85,格宾网箱支护后Fs=1.66，表明由于格宾护坡结构的放置，使边坡的稳定性系数略有减小，主要是由于格宾网箱的设置对坡面起到了压载作用，使边坡稳定性略有降低，但稳定性系数依然能够满足规范要求。

格宾网箱支护前、后边坡水平位移云图如图9、10所示。由图9、10可知，支护前边坡最大位移为17.8 mm，支护后为11.6 mm，由于格宾的支护作用使边坡最大位移减小35%，可见格宾网箱支护结构具有限制边坡位移的作用。

图7 预应力锚索格构梁护坡最大剪切应变云图 图8 格宾网箱护坡最大剪切应变云图

图9 格宾网箱支护前边坡水平位移云图 图10 格宾网箱支护后边坡水平位移云图

4 复杂条件下格宾网箱生态护坡稳定性分析

4.1 地震工况下格宾网箱生态护坡稳定性分析

根据《建筑抗震设计规范》(GB 50011—2010)[22]，拟建场区抗震设防烈度为7度，设计基本地震加速度值为0.10g，设计地震分组为第二组。采用拟静力法模拟水平地震作用，在所建模型基础上，施加水平朝向边坡外侧的0.1g水平加速度，进行边坡稳定(SRM)求解分析。求得水平地震作用下格宾网箱支护前、后边坡的潜在滑动面位置与无地震作用时相同，只是在水平地震力的作用下使第三级边坡坡脚最大剪切应变有所增大。格宾网箱支护后边坡稳定性系数Fs=1.33>1.15，说明地震作用下格宾网箱生态边坡处于稳定状态，与地震作用下格宾网箱支护前的Fs=1.46相比，稳定性系数减小了8.9%，减小幅度不大。在地震作用下，格宾网箱支护前边坡最大位移为38.6 mm，支护后边坡最大位移为21.0 mm，减小了45.6%，表明在地震作用下，对位移的限制尤其显著，格宾网箱支护结构具有良好的抗震性能。

4.2 降雨作用下格宾网箱生态护坡稳定性分析

参照我国水文部门对降雨量等级划分标准来综合确定模型采用的降雨方案。本文模拟采用“渗流/固结分析”模块的曲面流量建立边坡表面的流量边界，崇礼地区气象记载的最大降雨强度为45 mm/h，属于暴雨级别，结合崇礼地区降雨情况，设置曲面流量为45 mm/h，持续时间为4 h，时间步长为1 h，共进行4步数，总降雨量为180 mm。边坡降雨边界条件定义示意图如图11所示。

图11 边坡降雨边界条件定义示意图

由于模型需要分析降雨入渗对二维边坡稳定性的影响，所以在设置分析工况前需要建立类型为“应力-渗流-边坡”的施工阶段管理组，然后再设置求解类型为施工阶段的分析工况。在施工阶段的类型设置过程中，阶段类型为瞬态时，设置降雨时间及步长；阶段类型为应力时，选择边坡(SRM)选项，即采用强度折减法求解计算。经计算求得降雨入渗作用下格宾网箱支护后边坡稳定性系数为Fs=1.59，比相同降雨作用下格宾网箱支护前边坡的稳定性系数Fs=1.70略有减小，减小幅度为6.5%，但仍大于规范限值Fst=1.15，说明在降雨入渗作用下，边坡仍处于稳定状态。在降雨作用下，格宾网箱支护前边坡最大位移为21.2 mm，支护后边坡最大位移为14.0 mm，减小了34.0%，表明格宾网箱具有一定的限制边坡位移的作用。

4.3 地震与降雨共同作用下格宾网箱生态护坡稳定性分析

为探究地震与降雨共同作用下边坡的稳定性，采用与4.2节相同的数值模型及模型边界条件，建立类型为“应力-渗流-边坡”的施工阶段管理组，然后再设置求解类型为施工阶段的分析工况。设置施工阶段类型为应力时, 添加0.1g水平地震加速度，并勾选边坡(SRM)选项，采用强度折减法求解计算，其余设置的网格、边界条件和荷载均与4.2节相同。求得地震与降雨共同作用下格宾网箱支护后边坡稳定性系数Fs=1.28，大于规范限值Fst=1.15，说明在地震与降雨共同作用下边坡仍能保持安全稳定。与格宾网箱支护前边坡的稳定性系数Fs=1.35相比，在地震与降雨共同作用下，由于格宾网箱的放置使边坡稳定性系数减小了5.5%，格宾网箱支护前边坡最大位移为51.0 mm，支护后边坡最大位移为29.6 mm，减小了42.0%。

在复杂条件下，格宾网箱的支护作用使边坡的稳定性系数略有减小，减小幅度不超过10%，对于边坡整体稳定的不利影响较小。由于格宾网箱的支护作用，使边坡最大水平位移减小约35%，在地震作用下，水平位移减小幅度为45%，表明格宾网箱支护对边坡位移有显著的限制作用。

5 复杂条件下格宾网箱支护结构稳定性分析

格宾网箱支护结构体系受力如图12所示。结构受力包括自身重力G、边坡支持力FN、沿坡面向上的摩擦力Ff、底层网箱沿水平面向坡内的摩擦力Ff0、水平地震力Fe以及强降雨作用下产生的渗流力J。本文中坡脚处渗透性好，则渗流理想方向为与坡面方向相平行[23]。由于格宾网箱逐层缩进叠摞，故其相对应的护坡角度可视为α(图中坡面线与水平方向线的夹角)。

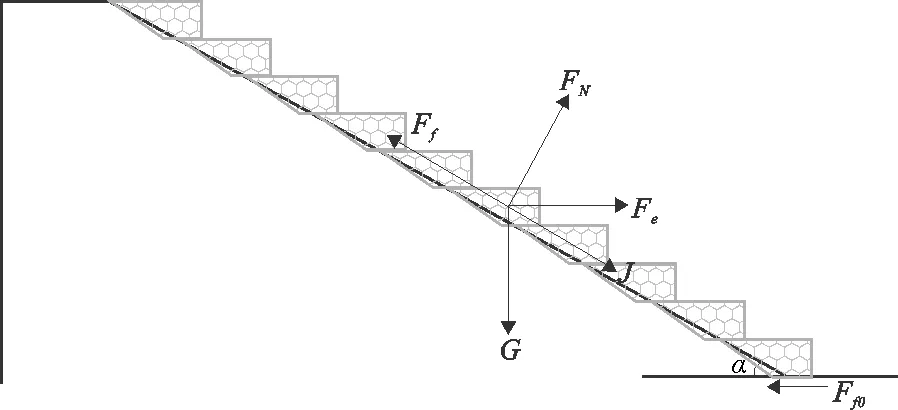
图12 格宾网箱支护结构体系受力示意图

格宾支护结构自身抗滑稳定性安全系数F的表达式为：

(1)

式中：R为结构自身抗滑力，kN；T为滑动力，kN。

根据受力平衡条件列出极限平衡方程：

R=Ff+Ff0cosα

(2)

T=Gsinα+Fecosα+J

(3)

式中：Ff为沿坡面向上的摩擦力，kN；Ff0为底层网箱产生的沿水平面向坡内的摩擦力，kN；Fe为水平地震力，kN；J为渗流力，kN。

设单层格宾网箱自重为G0、格宾网箱与坡面之间摩擦系数为μ，则：

Ff0=μG0

(4)

Ff=μ(Gcosα-Ff0sinα+Fesinα)

(5)

水平地震力根据《公路工程抗震设计规范》 (JTG B02—2013)[24]按下式计算：

Fe=CiCzKhG

(6)

式中：Ci为重要性修正系数，取值在0.6～1.7之间；Cz为综合影响系数，一般取0.25；Kh为水平向地震系数，根据地震基本烈度取值。

单位格宾网箱护坡宽度所产生的渗流力按下式计算：

J=γwtwLsinα

(7)

式中：γw为水的容重，kN/m3；tw为格宾支护结构中水位线高度，m；L为格宾结构护坡长度，m；α为护坡坡度，(°)。

将公式(2)～(7)代入公式(1)中，整理后得：

(8)

本文格宾网箱支护结构护坡坡度α=29°，格宾网箱与坡面之间摩擦系数取0.6[25]，抗震设防烈度设为7度，Ci取1.7，Kh取0.1，降雨作用按强降雨使格宾填料达到饱和来考虑，tw近似取0.34 m。由公式(8)格宾结构自身稳定系数计算公式，计算得到自然条件、地震、降雨以及地震与降雨共同作用下不同层数格宾网箱的结构自身稳定系数，计算结果如图13所示。

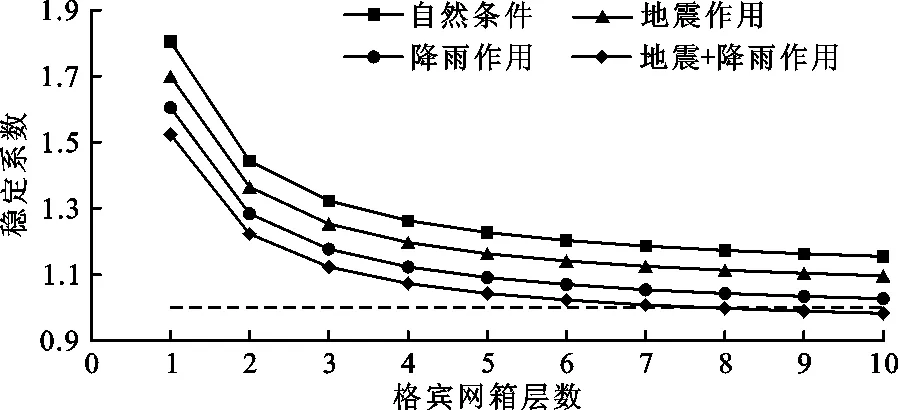
图13 各条件下不同层数格宾网箱支护结构的稳定系数

由图13可知，随着格宾网箱叠摞层数的增多，其自身抗滑移稳定系数曲线呈逐渐减小而后趋于平缓的趋势，在格宾网箱层数由1层增至3层时，稳定系数减小幅度显著；当层数由4层增至7层时，减小相对缓慢；当超过7层时，随层数的增加，曲线变化平缓，最终将趋于一个定值。根据公式(8)，在不考虑降雨、地震等复杂条件时，随着层数的增加，格宾支护结构体系自重增大，产生的滑动力也增大，而底层格宾提供的抗滑力不变，当层数足够多时，提供的抗滑力基本可以忽略不计，此时F=tanφ/tanα，即这一定值为格宾网箱与坡面之间的摩擦角(φ)正切值与边坡坡角(α)正切值的比值。

根据格宾网箱层数与稳定系数之间的规律可知，支护结构在自然条件、7度地震、强降雨作用下均能保持安全稳定，而在地震与强降雨共同作用下，最小稳定系数为0.98，略小于1，由此表明倒梯形的新型格宾网箱支护结构体系具有较好的自稳性。

6 结 论

依托2022年冬奥会国家跳台滑雪场高切坡工程，本文对在地震、降雨以及地震与降雨共同作用的复杂条件下，新型格宾网箱生态护坡的边坡整体稳定性及格宾网箱支护结构自身抗滑移稳定性进行研究，得出以下主要结论：

(1)对稳定的边坡采用格宾网箱生态护坡后，由于压载作用使边坡整体稳定性略有降低，无论自然条件还是复杂条件下，经格宾网箱支护后的边坡稳定性系数降低幅度不超过10%，格宾网箱对边坡整体稳定性的不利影响较小。

(2)经格宾网箱支护后可使边坡的最大水平位移减小35%，能够有效限制边坡位移，尤其在地震作用下，位移减小近一半，对位移的限制尤为显著。

(3)当格宾网箱层数少于7层时，其自身抗滑移稳定系数随格宾网箱叠摞层数的增加而减小；当格宾网箱层数超过7层时，稳定系数随层数的增加逐渐趋于定值。本文格宾支护结构自身稳定系数保持在1.2左右，具有良好的稳定性。

(4)新型格宾网箱支护结构体系具有良好的自稳性，且对边坡整体稳定性的不利影响较小，并起到有效限制边坡位移的作用，是一种能够较好适用于国家跳台滑雪场高切坡的生态支护结构体系，可为类似高山滑雪赛道工程的生态护坡提供参考。