斯特林循环中射流现象及其对循环特性影响

刘柏岙，王树林，肖 刚

（能源清洁利用国家重点实验室浙江大学能源工程学院，浙江 杭州 310027）

斯特林发动机应用前景较为广泛，其在余热回收[1-2]，由斯特林发动机构成的微型热电联产系统[3-5]和碟式斯特林发电系统[6-8]等方面受到关注。

段晨[9]建立了考虑“不可逆因子”的斯特林循环热力学模型，采用相似设计和多目标优化方法设计制造了1 台β型斯特林发动机。瞿凡等[10]基于1 台β型斯特林发动机，对加热器进行了辐射与燃烧2 种加热方式的数值模拟与优化设计。黄护林等[11]对斯特林发动机回热器进行数值模拟，研究了长径比和孔隙率对回热器有效性及流阻损失的影响。王思[12]考虑回热器内部辐射换热，对丝网结构及材料物性进行数值模拟，得到丝网材料比热容的最优值。Dellali 等人[13]对振荡流条件下，柱阵列回热器的压降进行实验研究，推导了回热器摩擦系数的实验关联式。目前，对于斯特林发动机的研究集中在整机循环特性实验研究、斯特林循环分析方法、回热器流动与换热特性研究等各个方面。

在斯特林发动机运行过程中，工质在各个部件间循环流动，流动过程中不可避免地会发生射流现象，并产生一定的功损失和热损失。尤其是在回热器与加热器、冷却器接口部分的间隙内产生的射流现象，直接影响了工质在回热器内的流动与换热情况。基于三维数值模拟，本文研究了斯特林发动机内的射流现象对斯特林循环的影响及损失机制，并对回热器部分进行了结构优化设计，最后依托1 台百瓦级β型斯特林发动机，对不同工况下的模拟结果进行了实验验证。

1 斯特林发动机三维数值模型

基于Ansys CFD 软件，对斯特林发动机内复杂的流动换热情况进行三维数值模拟。使用Ansys DesignModeler 建立几何模型，并创建流体计算域。基于ICEM CFD 进行了全结构化网格的生成。利用Ansys Fluent 18.0 软件进行数值计算。

1.1 几何模型与网格划分

考虑到几何与流场的对称性，为了提高计算精度与计算效率，构造了1/4 几何模型如图1所示。对照β型斯特林发动机的设计制造参数，确定了流体域的几何参数，并进行了全结构化网格划分，结果如图2所示。

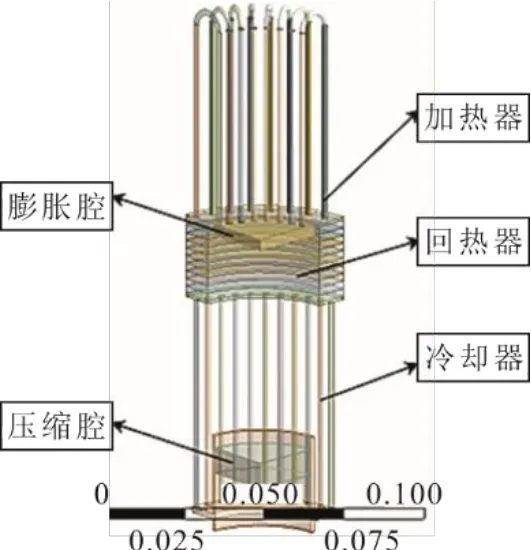
图1 斯特林发动机几何模型（m）Fig.1 Geometric model of Stirling engine(m)

图2 斯特林发动机网格划分Fig.2 Mesh generation for the Stirling engine

在相同的几何模型上，生成了不同尺寸和数量的3 种网格，其网格数分别为153.6 万、506.8 万和1 247.6 万。计算过程中发现，3 种网格计算所得的温度、压力、循环效率和循环指示功均有良好的收敛性。在其他条件相同的情况下，循环效率和循环指示功随网格数目的变化如图3所示。从图3 可以看到，506.8 万网格与1 247.6 万网格之间循环效率相对误差0.75%，循环输出功相对误差0.87%。综合考虑计算精度与计算所需资源，本文选择506.8 万网格进行计算。

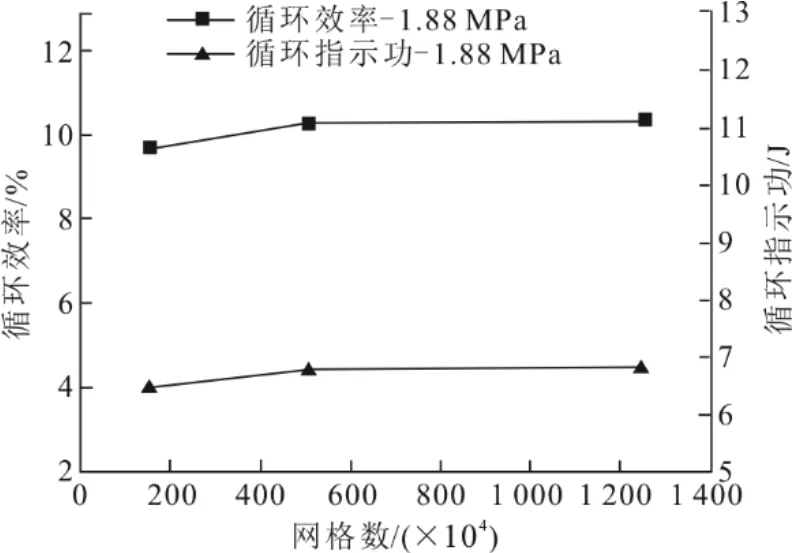
图3 网格无关性验证Fig.3 Grid independence verification

1.2 三维数值模拟求解器设置

综合考虑百瓦级β 型斯特林发动机的几何构造、多孔介质区域以及运动部件动网格，以氮气为工质，将求解器类型设置为瞬态、压力基，选择SIMPLE 算法，选择具有相当精度的Standardk-ε湍流模型。对应实验工况参数设置三维数值模拟的边界条件见表1。

表1 三维数值模拟边界条件Tab.1 Boundary conditions for three dimensional numerical simulation

本模型是利用流体计算域边界的运动，模拟实际斯特林发动机中配气活塞和动力活塞的运动，使用动态层方法（Laying）对边界上的网格进行更新，同时利用用户自定义函数（UDF）指定边界运动，结合斯特林发动机菱形传动设计参数和DEFINE_CG_MOTION 宏，定义模型中配气活塞和动力活塞的运动。

该模型利用Fluent 软件自带的多孔介质模型，模拟实际工质在金属丝网回热器部分的流动状况。多孔介质模型简化了多孔结构，求解时在动量方程中增添由动量损失项和惯性损失项组成的动量源项。

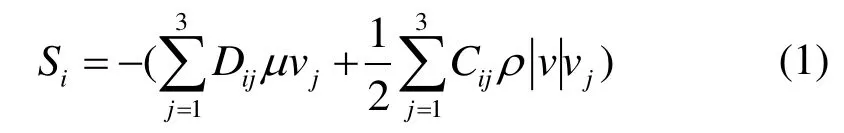
式中，Si代表i方向动量源项，代表黏性阻力代表惯性阻力。引入Tanaka 等人[14]关于回热器流阻系数f的经验关联式

最终计算得到主流方向上的黏性阻力系数Cf和惯性阻力系数Cj：

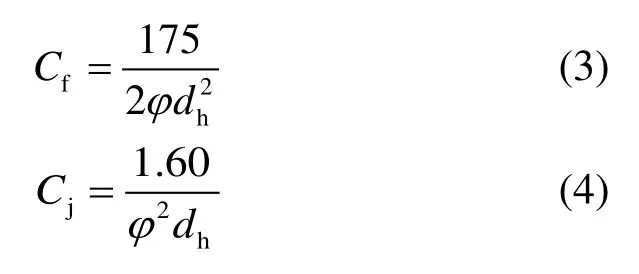
式中，φ为孔隙率，dh为金属丝网水力直径。

对于简化为多孔介质模型的回热器传热过程，本模型基于非热平衡假设，利用用户自定义标量方程（UDS）定义额外的标量输运方程，并计算流固间换热过程，其中固体能量方程如下：

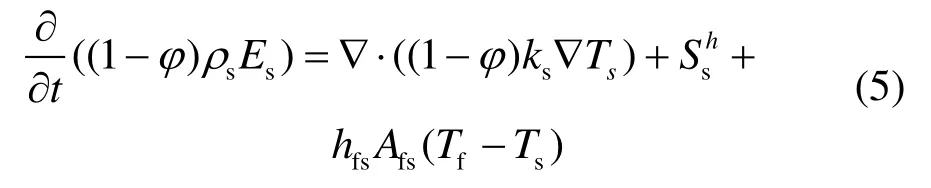
式中，h为流固间对流换热系数，ρs为固体密度，Es为固体介质总能，ks为固体介质导热系数，Ts为固体介质温度，Tf为流体温度，hfs为流固间对流换热系数，为源项。

引入Gedeon 等人[15]采用瞬时局部雷诺数描述的换热关联式。

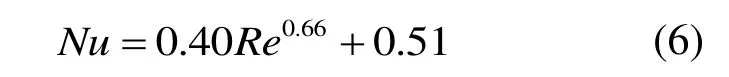
通过分别计算固相非稳态项、固体热扩散相、考虑径向热扩散的流体热弥散项和能量方程源项，最终得到多孔介质区域流固耦合换热情况。

1.3 斯特林发动机内部流动与换热特性

基于斯特林发动机三维数值模拟，对特定工况（N2-1.88MPa）和曲轴某一特定角度（33.26°）下，斯特林发动机内部温度场和流场进行了研究。在曲轴转角为33.26°下，斯特林发动机膨胀腔体积接近最小值，正处在压缩腔体积减小，膨胀腔体积增大，工质由压缩腔流向膨胀腔的所谓“冷吹”过程。

斯特林发动机内温度分布如图4所示。由图4可见：膨胀腔和加热器内工质温度较高，压缩腔和冷却器内温度较低；回热器部分温度由热端到冷端沿轴向下降，同时在冷吹过程中，回热器内部工质流向加热器被加热。

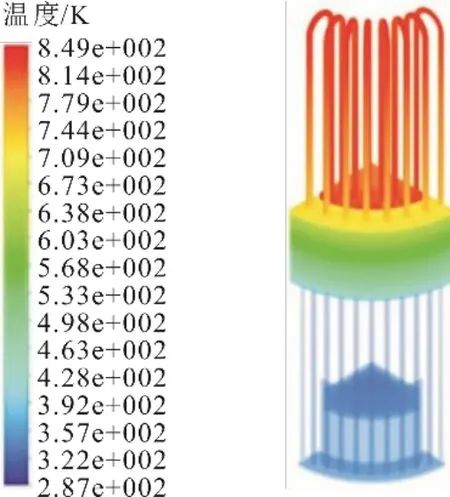
图4 斯特林发动机内温度分布Fig.4 Temperature distributions in the Stirling engine

图5 为斯特林发动机内速度流线。

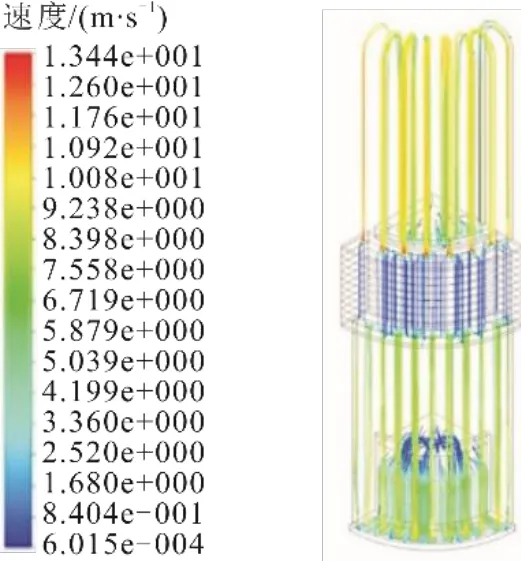
图5 斯特林发动机内速度流线Fig.5 Velocity streamlines in the Stirling engine

由图5 可以看出，在“冷吹”过程中，加热器和回热器、冷却器和压缩腔之间的连接处和加热器弯管处，工质流速最大，膨胀腔和压缩腔内工质流速较小，回热器内工质的流速最小。在“冷吹”过程中，配气活塞和动力活塞的运动迫使工质从加热器流向膨胀腔，由于横截面积的变化，在加热器和膨胀腔接口处以及冷却器与回热器接口处工质流速迅速增大，产生较为明显的射流现象。

2 斯特林发动机内射流现象与回热器结构优化

2.1 膨胀腔内射流现象及其影响

在“冷吹”过程中，加热器内高温工质进入膨胀腔内并产生较为明显的射流现象，膨胀腔内密度分布如图6所示。由图6 可见，膨胀腔内密度分布高度不均匀。由射流现象导致的密度分布，与斯特林发动机内部平均压力密切相关。模拟结果显示，在整个斯特林循环过程中的平均压力越大（1.41、1.88、2.36 MPa）参与做功的工质质量越大，同时平均压力的增大使密度分布的不均匀性更加明显，膨胀腔内的工质密度差也越大（0.372、0.507、0.642 kg/m3）。平均压力的增大显著增强了加热器高温工质射流进入膨胀腔内的传热过程，增强了冷热工质混合作用。

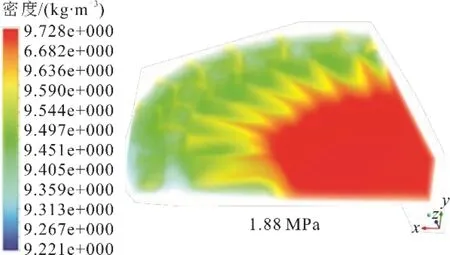
图6 膨胀腔内密度分布Fig.6 Density distributions in the expansion chamber

对于膨胀腔内的射流现象，另一个重要的影响因素则是转速。转速的改变直接影响了斯特林发动机工作腔中工质的流速，膨胀腔内工质速度矢量分布如图7所示。

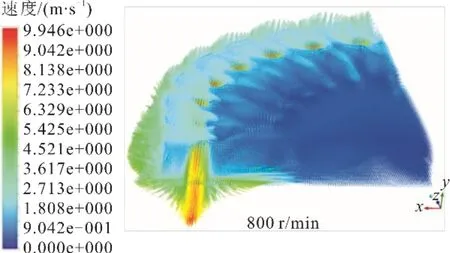
图7 膨胀腔内工质速度矢量分布Fig.7 Velocity vectors in the expansion chamber

由图7 可见，在加热器与膨胀腔接口部分，工质流速最大，同时在这部分高速工质和膨胀腔壁面之间，存在速度较小的漩涡。由模拟结果得到，随着转速的增大（600、800、1 000 r/min），由加热器流向膨胀腔的工质的流速不断增大（最大流速分别为7.64、10.04、12.44 m/s），工质的射流冲击作用更加强烈，产生的漩涡及能量耗散也更多。

2.2 回热器顶端间隙内射流现象及回热器结构优化

在回热器与加热器、冷却器的连接部分存在一定大小的间隙。以“冷吹”过程为例，工质由冷却器流向回热器，在丝网顶面间隙内发生射流现象（图8）。

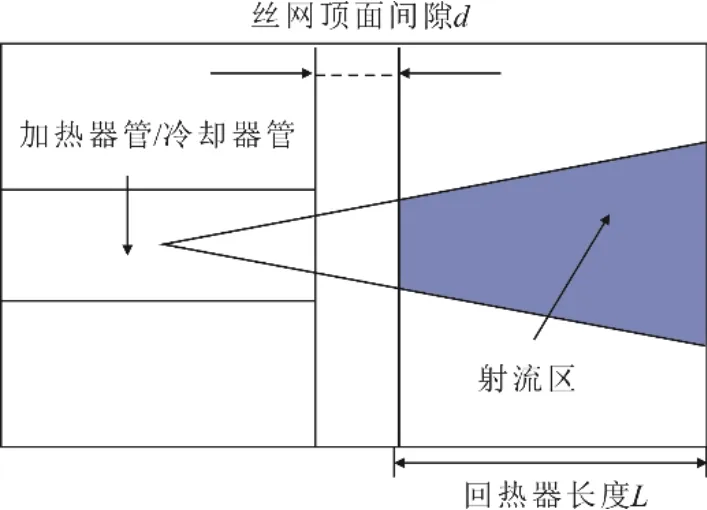
图8 回热器内射流现象示意Fig.8 Jet impingement in the regenerator

定义回热器间隙长度比λ为

式中，d为丝网顶面间隙长度，L为回热器长度。当前斯特林发动机回热器间隙长度比λ设计值为0.074。为进一步研究回热器顶端间隙内射流冲击对斯特林循环特性的影响，分别设置6 组不同λ值0、0.037、0.074、0.130、0.167 和0.259，进行三维数值模拟。不同回热器间隙长度比下循环效率变化如图9所示。

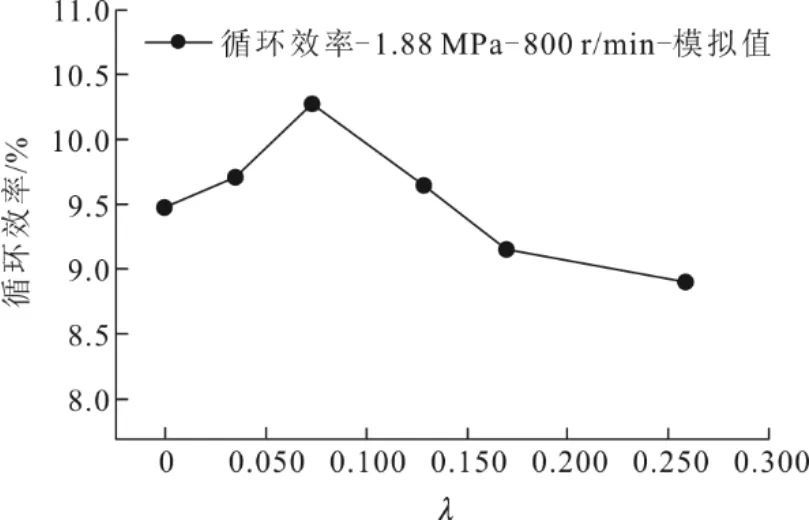
图9 不同回热器间隙长度比下循环效率变化Fig.9 Changes of the cycle efficiency at different ratios of regenerator gap length

由图9 可见，当λ值范围为0.037～0.167 时循环效率较大，与回热器顶端无间隙的情况（λ=0）相比，当λ=0.074 时，循环效率提高了8.32%。

不同回热器间隙长度比下工质流速分布如图10所示。

图10 不同回热器间隙长度比下工质流速分布Fig.10 Velocity distributions at different ratios of regenerator gap length

由图10 可见：在冷吹过程中，当λ=0，即回热器顶端无间隙、无射流现象时，工质直接从冷却器流入回热器，并只流过回热器的一小部分基体，使回热器的回热效果受到一定影响（循环效率η=9.50%）；当λ=0.074 时，工质在回热器顶端间隙内发生射流现象，在较广的区域内流入回热器（循环效率η=10.29%）；当回热器顶端间隙进一步增大，λ=0.259 时，在回热器顶端间隙内出现了较为明显的漩涡，工质做功能力下降（循环效率η为8.90%）。

回热器顶端间隙内射流现象的存在，一方面使工质更加充分地流入回热器，提高了回热效率；另一方面使间隙内产生漩涡，造成工质做功能力的下降。因此，以提高循环效率作为回热器结构优化目标时，该斯特林发动机存在最佳回热器间隙长度比λ，其值范围为0.037～0.130。

3 百瓦级β型斯特林发动机实验验证

3.1 实验系统组成及测点布置

实验系统由加热装置、百瓦级β型斯特林发动机主体以及数据采集装置3 部分组成。百瓦级β型斯特林发动机主要由飞轮、菱形传动机构、动力活塞、配气活塞、冷却器、回热器和加热器组成。实验测点布置及三维结构如图11所示。

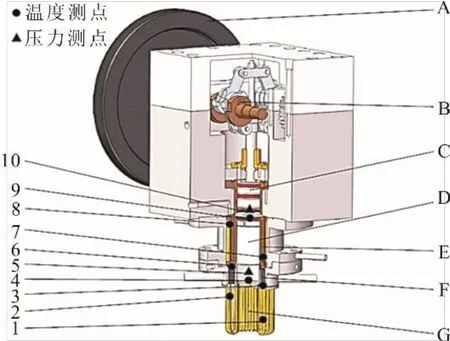
图11 β型斯特林发动机结构示意Fig.11 Schematic diagram of β type Stirling engine

以氮气为工质，采取盐浴方式加热并使用冷却水进行冷却，在一定转速和充气压力范围内进行实验。具体实验设计工况见表2。

表2 实验台实验工况Tab.2 Experimental working conditions for test bench

3.2 模拟结果实验验证

在本文中，利用循环指示功Win，循环输出功率P和循环效率η3 个指标来衡量斯特林循环特性。Win代表1 个循环周期内，即曲轴旋转1 周，工质完成1 次膨胀压缩的过程中，斯特林发动机对外输出功。pi代表1 个循环周期内采集到的压力信号，Vi代表对应的工作腔体积，n代表1 个循环周期内采集到的数据组数。在1 个循环周期内，对n组压力平均值与对应的体积差值的乘积进行累加求和，得到Win。

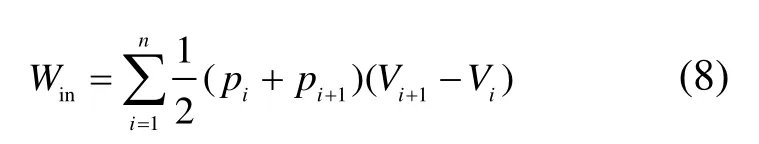
式中P代表在单位时间内，斯特林发动机的对外输出功，可根据转速υ和Win得到。

η综合衡量了斯特林循环过程中流动与换热损失，利用冷却功率Qco和循环输出功W可以得到[16]。

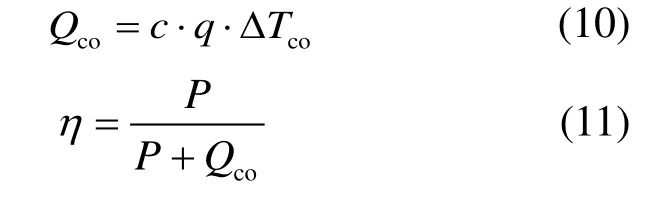
式中，c为冷却水的比热容，q为冷却水流量，ΔTco为冷却器进出口水的温差。

在实验条件下数值模拟结果与实验结果对比如图12、图13所示。由图12、图13 可见：在转速相同且压力不同的情况下，Win的相对误差范围为3.00%～5.78%，η的相对误差范围为5.89%～9.91%；在压力相同且转速不同的情况下，Win的三维数值模拟结果与实验值的相对误差范围为 3.58%～7.72%，η的相对误差范围为5.48%～9.89%。可见，模拟结果与实验结果一致性较好。

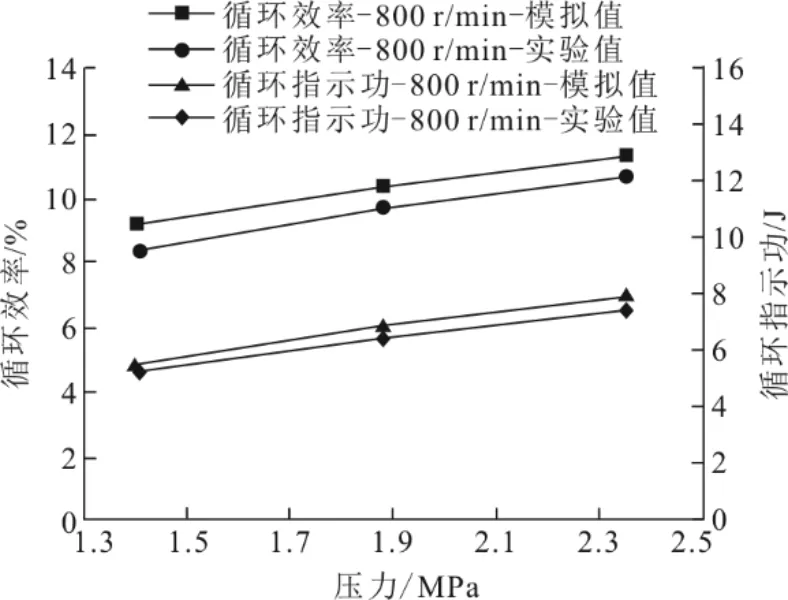
图12 不同压力下数值模拟结果与实验结果对比Fig.12 Comparison between the numerical model results and experimental results at different pressures

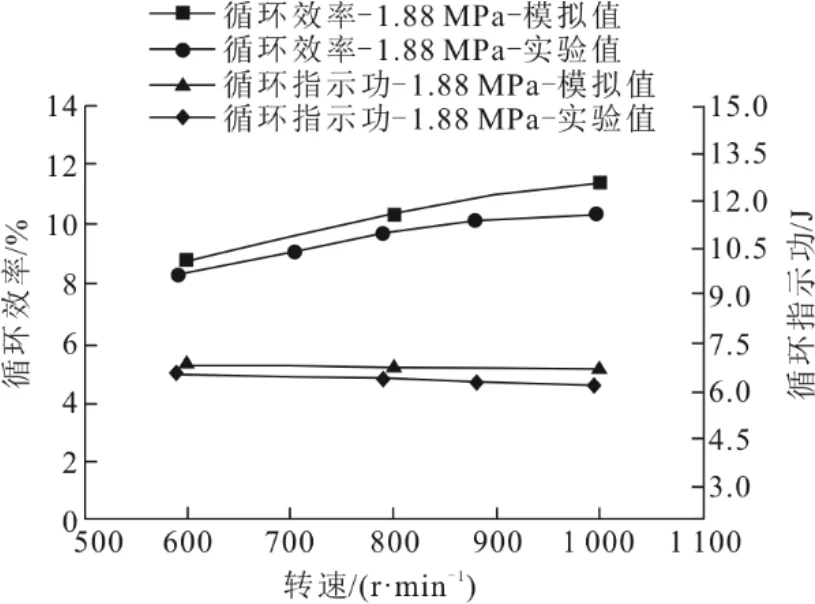
图13 不同转速下数值模拟结果与实验结果对比Fig.13 Comparison between the numerical model results and experimental results at different rotating speeds

由图12、图13 还可见：在实验条件下，压力增大，循环指示功和循环效率越大；转速增大，循环指示功减小，循环效率增大但增长幅度减小。

4 结论

1）三维模型与实验结果具有较好的一致性，其结果均显示，对于百瓦级β型斯特林发动机，在一定范围内增大平均压力，可增大斯特林发动机中工质质量，同时增强射流现象所导致的工质分布不均匀，以及冷热流体混合和传热过程，从而增大循环指示功，提升循环效率。增大斯特林发动机转速，会增大工质流速，使得工质射流过程更加明显，漩涡产生的能量耗散更大，从而减小循环指示功，增大循环输出功，循环效率增大但增幅较小。

2）在工质由压缩腔流向膨胀腔的“冷吹”过程中，加热器内工质进入膨胀腔发生射流现象，冷热工质混合导致膨胀腔温度分布不均匀，并产生冲击作用和漩涡，使工质做功能力下降。

3）回热器顶端间隙内射流现象影响了工质在回热器内的流动与换热，回热器间隙长度比λ存在1 个最佳范围，使斯特林发动机循环效率最大。在本研究中λ由0 增至0.037～0.130 时，对应的最高循环效率比提高了8.32%。