时间触发分布式实时系统容错时钟同步算法设计

关博文，朱长昊，张凤登

（上海理工大学光电信息与计算机工程学院，上海 200093）

0 引言

随着计算机系统以及大规模集成电路的不断发展，分布式系统越来越多地应用在人们的日常生活及工业生产中［1-2］。分布式系统从网络类型上可分为时间触发（Time Trigger，TT）系统和事件触发（Event Trigger，ET）系统［3］。事件触发系统基于事件的发生触发动作，时间触发系统基于既定的时刻表或事件调度器的调度，在某个精确时刻触发动作。为保证系统的实时性以及应对突发事件的鲁棒性，通常会同时采用这两种结构，如FlexRay 与Ethernet 网络等。从时域上分布式系统又可分为实时系统与非实时系统，实时系统又可进一步分为强实时系统和弱实时系统［4］。本文所研究的是在时间触发分布式实时系统环境下的时钟同步算法。

在时间触发分布式实时系统中，各个节点通常需要大致同时执行某些动作。在这样的系统中，每个处理器通常都拥有自己的独立物理时钟，它们相对于实时都具有一定的偏移率［5-6］。即使让所有节点的物理时钟同时启动，随着时间的推移，这些节点上的物理时钟也会偏移实时时间。因此，时钟必须定期重新同步。在进行设计时钟同步算法时，不仅要考虑因时钟老化等物理因素引起的时钟不同步问题，还要考虑节点的时钟出现故障或者节点本身出现故障的问题。本文将节点和链路故障进行简化，统一假设为节点的时钟故障问题［7］。此外，还要容忍系统中的节点为拜占庭将军问题时的情况。

过去研究中最为经典的是Lamport 等［8］的交互式算法——CNV 算法和交互式一致性算法——COM、CSM 算法。这两类算法可在任意时钟故障情况下工作，其中包括出现时钟拜占庭故障。但是CNV 算法要求出现故障的进程数量不能超过分布式系统总数量的1/3；COM 和CSM 算法虽然能够在故障节点数量少于总结点数一半的情况下保持时钟同步，但是需要额外的硬件来提供消息的数字签名。维也纳大学的Kopetz 等［9］分析了CNV 算法并在硬件上测试了该算法；Ramanathan 等［10］、Shin 等［11］提出一种硬件辅助软件时钟同步的方法，其软件同步算法部分借鉴了Lamport 的交互式收敛算法，硬件部分主要实现同步消息的发送和接收，以及记录同步信息的本地时间戳。最终实验表明，采用这种软硬件结合的方法比纯软件同步算法效果更好，精度提高2 个数量级以上，但是增加了经济上的开销。在大型分布式系统中，其硬件开销会成倍增长。

本文提出一种收敛性软件时钟同步算法，该算法不需要额外增加硬件开销，并且它的修正效果相比于容错中值时钟同步算法更为明显。

1 模型设计

1.1 时钟同步模型建立

在描述本文的容错性内部时钟同步算法之前，首先建立一个系统模型，该模型遵循一个宽泛的通用范例［12］，具体就是读取远程时钟技术。读取远程时钟技术分为两大类：①基于请求回复机制的远程时钟读取技术（Remote clock reading，RCR）［13］，其大体步骤如下：进程pj估算远程进程pi的时钟，向pi发送一个请求消息，并等待一段确定的时间来获取pi的回复；②基于初始同步的时钟检测技术（Time Transmission，TT），每轮重复执行同步算法。节点在某个设定的时刻发送包含其时间信息的消息，而不需要先发送时间请求［14］，其代表模型由Lundelius 和Lynch 提出，故通常称为LL 模型。

由上述文献可知，基于第一种技术的模型存在的最大估计误差为2D(1+2ρ)-2(δ-ε)，基于第二种技术的模型最大估计误差为2(ε+β+ρδ)，其中D 以pj的发送与pi回复这一过程用时的一半为值；ρ是时钟漂移率；δ是可能的消息延迟范围中值；ε是消息延迟的不确定度；β是初始时刻节点间的同步程度。

由于时间触发分布式实时系统是基于时间触发来发送节点的时间信息，不需要请求回复，因此相较于第一种模型，LL 模型的通信开销更小。但是相比于第一种模型，因为节点不知道下一条时间消息将由哪个节点发出，所以增加了读取误差。但若在非点对点网络，如广播式网络中就不存在该问题。因此，本文采用广播式通信的LL 模型。LL 模型对重同步周期TP 及节点的初始状态有一定要求。

1.1.1 基本假设与前提条件

在建立模型并分析算法前，需要对模型做相应假设，同时应用相应的定理以简化算法的性能分析。

令P 表示系统中节点的集合，由前文可知，其中每一个节点pi∈P 都有一个对应的本地硬件时钟，用Hpi表示。该时钟通常由一个晶振和不断计数增加晶振器节拍的计数器组成。虽然时钟是离散的，但所有算法都假设时钟连续运行，如Hpi是一段实时间隔的连续函数。此外，虽然硬件时钟由于温度改变和老化会偏离真实时钟，但通常假设其与真实时间的偏移量在一个很小的范围内，因此本文做如下假设：

假设1 本地硬件时钟漂移率假设：存在一个极小的常数ρ >0，定义对任意时刻t，所有硬件时钟Hpi(t)与ρ的关系如下：

其中，Hpi(t)表示处理器pi 在真实时间t时的本地硬件时钟值，ρ称为硬件时钟的漂移率。该假设表示任一节点的本地硬件时钟与真实时间的偏差存在一个极小范围，其上限是ρ，即硬件时钟的漂移率存在一个合理范围，若超过该范围，可能没有算法能够将时钟同步回来。

假设2 通信链路全链接：节点间通过广播的方式进行通信，且任一节点pi∈P 在网络中发送的消息最终都能到达其目的节点，即模型不存在链路丢失故障。

在分布式系统中，根据不同的网络类型以及对网络负载所作的假设，消息延迟可能或多或少是可预测的［15］。本文假定存在的传输（如发送、传播、接收）延迟的上下限已知。

假设3 传输延迟有界：通过任何链接发送、传输与接收任何消息与真实时间的通信延迟Td存在一个已知的边界。即：

其中：δ为消息可能延迟范围的中值，ε为消息延迟的不确定度。当上述假设成立时，时钟同步算法保证了所有正确的逻辑时钟间的最大差值在一个范围内，即精密度γ。这也是确定性算法的显著特征——通过对通信延迟的上下限做出假设来得到一个定量的精密度值。

假设4 故障节点数有限：时钟同步算法执行过程中最多存在n个故障节点，其中n是一个正整数。由文献［16］可知，当系统中故障节点数超过总节点数的1/3 时，在不使用外部数字签名的技术下，将无法维持时钟同步。因此，对假设4 进一步假设：系统由m个节点组成，其中的故障节点数为n，它们的关系是：

假设5 算法执行时间：消息延迟除了假设3 中所提的传输延迟外，还存在一系列延迟，如任一节点pi∈P在网络中发送的消息前生成消息所需时间，接收消息后解析消息所需的时间，以及执行同步算法所需的时间。本文假设这些时间都可忽略。通常情况下，造成消息延迟的主要原因是传输延迟，而上述的延迟都与节点的处理器有关，简化起见，将忽略这些延迟。

假设6 初始同步：设T0表示节点时钟时间的初始时刻表示p节点在初始时刻的真实时间，那么系统中的非故障节点在一开始时是同步在某个固定先验范围内的。即：

其中为一个定值，p和q为非故障进程。

假设7 同步周期限制条件：为了使同步中非故障节点p发送消息时其余的非故障节点q都与p处于同一轮次，重同步周期TP要满足以下条件：

其中，ρ为时钟漂移率；δ为可能的消息延迟范围中值，ε为消息延迟的不确定度。β为一先验常数，表示初始同步程度的上限。

假设8 初始化同步程度限制条件：

若未特殊指明，本文的其它假设与前提条件都与LL 模型一致［20］。

1.1.2 模型描述

如上述假设及条件所述，系统内节点全链接，即可以通过广播的方式发送消息。算法将在一系列轮次中进行，也就是说，将逻辑时钟以轮次的形式表示。每轮的时间长度恒定，用L表示，由k个宏时隙组成，其中k＞0。即：

因为每一轮都进行一次时钟同步，因此其长度也要满足上述重同步周期条件。每轮要留出固定长度的时间作为修正段，通常称为NIT 段。在NIT 段内节点执行逻辑时间状态修正与速率修正，因此在该时间段内通常不执行任何事件。以4 个节点在理想状态（即完全同步）下为例说明第i轮结构，节点的相关参数如表1 所示。

系统包含一类特殊消息：同步消息Mp，其中p为系统内任一节点。因为采用了上文所述的消息传输技术（TT），因此系统的时钟同步通过时间触发的方式进行。在轮次i中，i≥0i，每个节点都存在一个互不相同的同步时刻。当本地硬件时钟达到时就发送同步消息Mp，节点q一旦收到Mp就记下本地时钟观测的该时刻

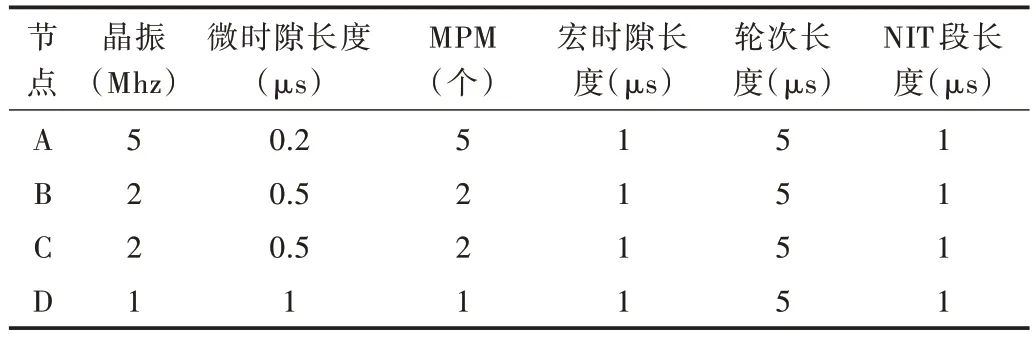
Table 1 Node parameter表1 节点参数

根据表1，各节点第i轮情况如图1 所示。其中mtj表示节点第j次宏节拍，也就是相应逻辑时钟的第j个节拍。TNIT表示系统进入NIT 段时的时钟时刻。系统内各节点的同步时刻都是可知的，即根据不同的网络和应用需求通过离线设定所得。由可得出在第i轮同步中，节点q观测的p与q的本地时钟状态差，而根据便可得出节点q观测的p与q的速率差。在得出与各节点的状态与速率差后，即可应用收敛算法得出修正值，并在NIT 段应用该修正值，完成修正。

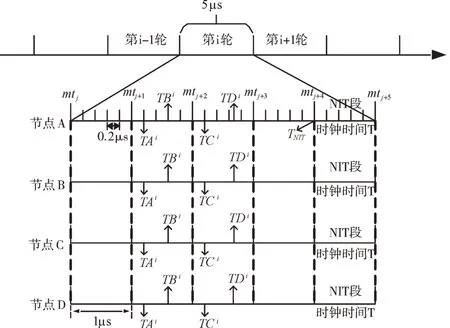
Fig.1 State of round i in ideal state图1 理想状态下第i 轮状态

值得注意的是，该结构与FlexRay 十分相似，其原因是FlexRay 同样也是基于LL 模型，所以准确来说，基于LL 模型的协议都具有相似的结构。同时，FlexRay 分为动态段与静态段。在静态段内，节点只能在相应的时隙内发送消息，而本模型则不存在该规则，节点可以在任何时刻发送同步消息。此外，关于为何要将逻辑时间分为轮次的形式也是一个值得探讨的问题。究其原因，主要是为了与外部时基进行统一，换言之，系统总是为用户服务的。而分轮次类似于日常生活中将时间分为年、月、日、分、秒的做法，便于用户的时间与系统的时间相对应。其次，轮次的结构也便于进行节点间的周期测量，使得节点可以获得与其它节点的速率差，从而进行速率修正。

1.2 容错性最值算法

1.2.1 算法提出

基于LL 模型的容错最值算法思路与LL 模型原始的容错均值算法类似，不同之处在于容错最值算法能够更快完成收敛，使得时钟间能够更快达成一致。相应地，其代价是实现的最坏情况下精密度略低于容错中值算法。

如上文所述，利用收敛函数计算修正项进行容错时钟同步的算法，其容错性的保证实质上在于对修正值的限制。不论是容错中值算法直观地对修正项大小进行限制，还是容错均值算法隐性地在计算过程内部进行限制，都是如此。同样，容错最值采用与容错中值算法类似的对修正值大小进行隐性限制，以保证算法的容错性，即在故障节点不超过总节点数1/3 的情况下，使得非故障节点的时钟仍维持在某个精密度下的同步。

1.2.2 算法过程

下面以伪代码的形式描述第i轮同步中节点q的容错最值时钟同步算法过程。

（1）函数及符号定义（见表2）。

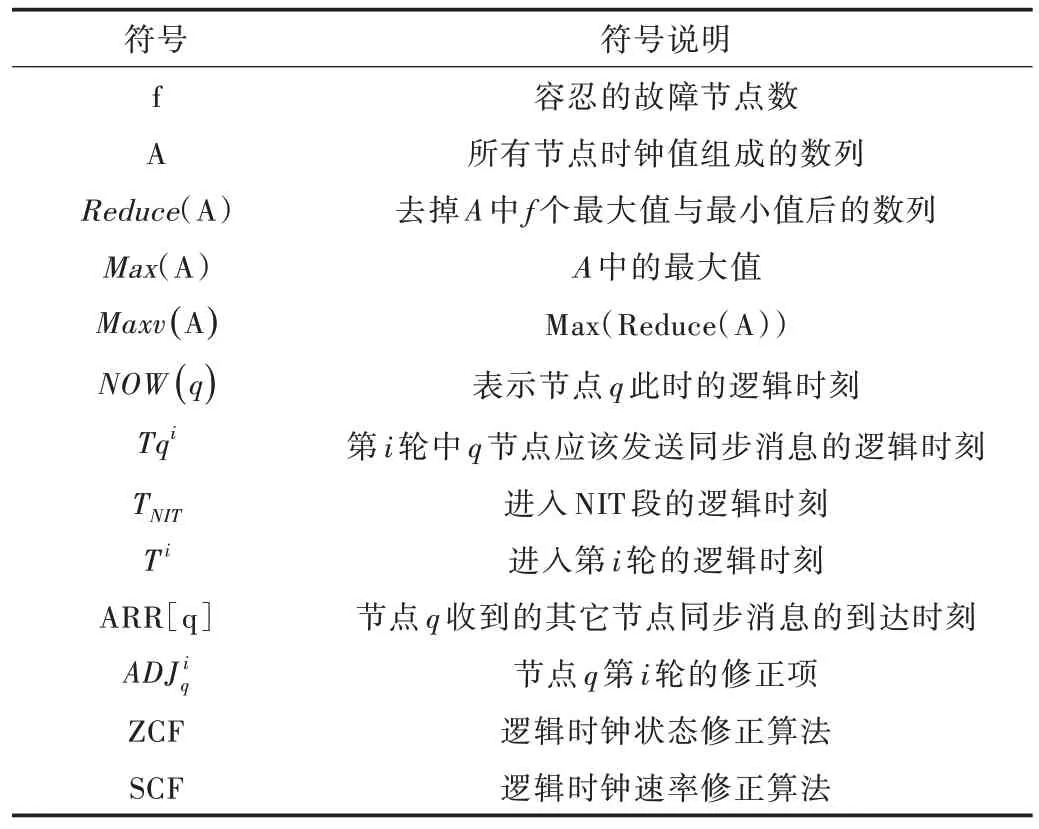
Table 2 Pseudocode parameter表2 伪代码参数

（2）算法描述。

算法：容错最值算法

输入：重同步时间

输出：修正后的节点时钟值

综上，通过舍弃掉q节点与其它节点时钟差值的f个最大值与f个最小值，将余下值中的最大值作为修正值，然后通过修正，实现容错性内部时钟同步。容错最值算法比容错均值算法少了一个排序的过程，在节点数目较多的情况下可以有效节省计算时间。同时，其收敛速度将快于容错均值算法与容错中值算法，这是该算法的显著特点，但其代价是精密度降低。相对而言，本同步算提供了一种新的思路，在不同场景下使得分布式系统的设计者能够多一种选择。

2 实验验证

2.1 仿真系统构成

对基于LL 模型的容错中值时钟同步算法及容错最值时钟同步算法进行仿真实验，采用专业的现场总线仿真测试工具CANoe 软件进行仿真测试，从实验的角度验证算法理论的正确性。将4 个节点构成一个总线型网络，网络中各节点通过广播方式进行通信。节点1、2、4 为正常节点，节点3 为拜占庭故障节点，即两面性时钟节点，其网络结构如图2 所示。

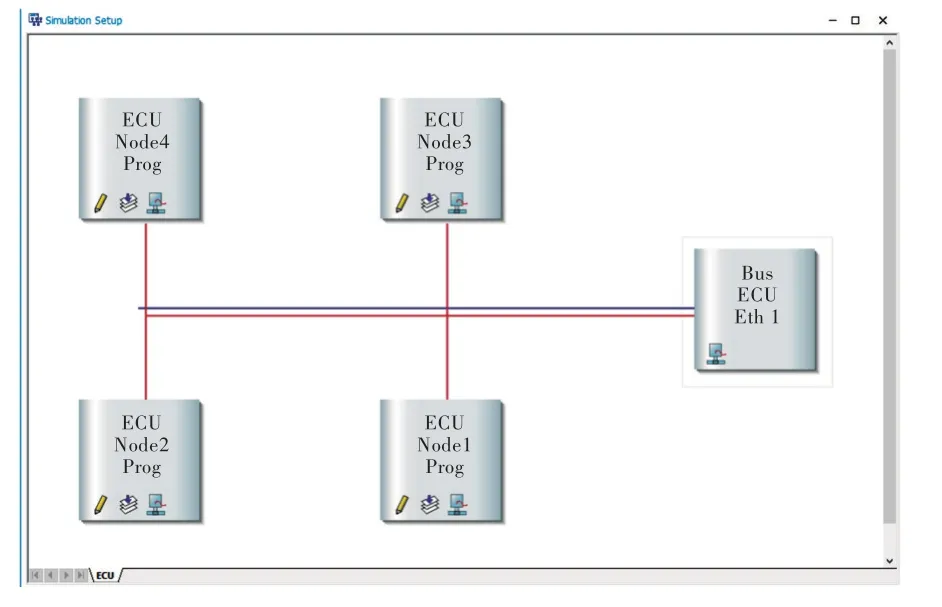
Fig.2 Simulation system network structure图2 仿真系统网络结构

实验中一共有7 条消息，其中4 条是算法相应节点必须发送的同步消息，余下3 条消息用于软件观测同步后节点时间差，并非算法所需。同时建立相应的环境变量来表示定时器模拟的节点逻辑时钟。算法相应的发送接收关系及消息ID 等关系定义见表3。

2.2 仿真系统参数

在搭建好实验系统网络框架后，需要确定具体参数。根据之前的研究成果［17-18］及LL 模型的基本约束条件，确定部分系统参数如下：系统容忍的最大漂移率ρ=10-4s，系统内传输延迟最大为10×10-6s，最小延迟为5×10-6s，即系统的消息延迟在μs 内［19］。系统内消息延迟不确定度ε=2.5×10-6s，消息延迟范围的中值δ=7.5×10-6s。根据LL 模型初始同步的基本约束条件式（3），忽略量级过小的参数，在上述条件下系统内初始同步程度βs，因此设系统内初始同步程度β=12×10-6s。再根据LL 模型同步周期的约束条件式（5）及式（6），忽略量级过小的参数，得出系统同步周期TP 的下限量级微秒级，而上限为TPs，即5ms。设系统内每轮同步长度即同步周期TP=0.22ms=220μs，参数如表4 所示。

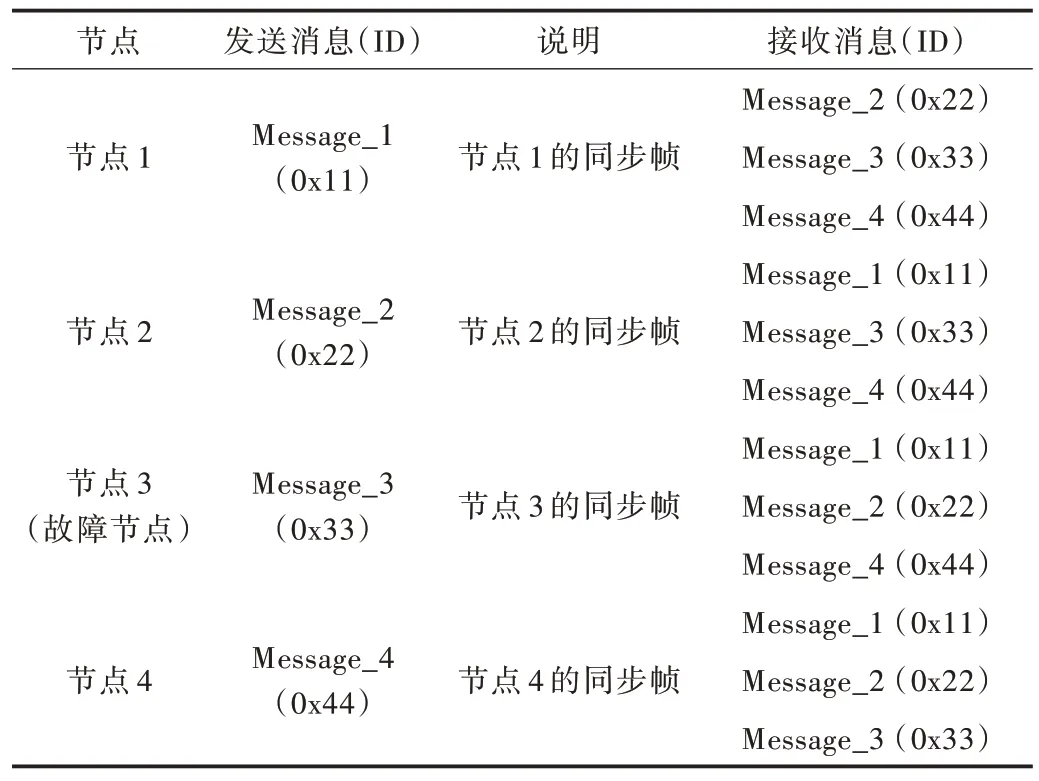
Table 3 Algorithm and message description表3 算法及报文说明

Table 4 System parameter表4 系统参数

根据文献［20］及前述结论，将表4 中的参数代入精密度计算公式，可得在上述配置下基于LL 模型的容错中值时钟同步算法的精密度为：0.014 512 4ms，即14.512 4μs；本文提出的容错最值时钟同步算法精密度为0.020 512 4ms，即20.512 4μs。同时根据表4 得节点间的具体参数配置如表5 所示。

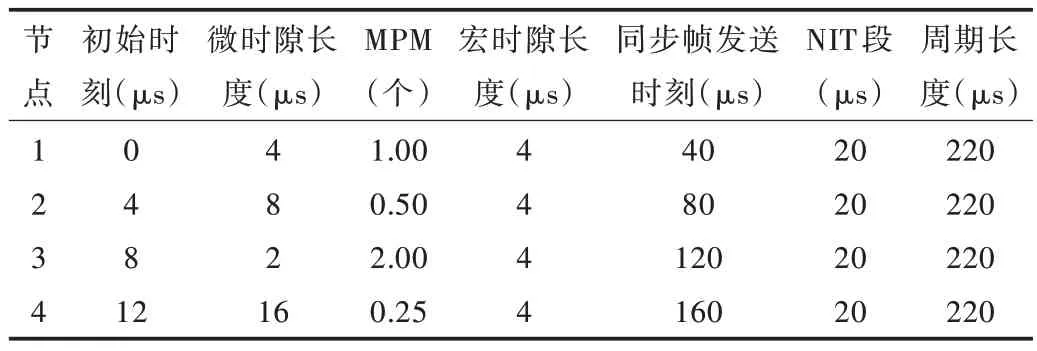
Table 5 Node parameter configuration表5 节点参数配置

2.3 基于LL 模型的容错中值算法（FTM）仿真结果

根据上述配置搭建系统并运行，使e1、e2、e3、e4 表示节点1 计算的与相应节点的逻辑时钟差值，而mid为据此得出的中值，Mtick为修正后的单位宏时隙长度，其中节点3为拜占庭故障节点，故e3 的值为随机值。e12、e13、e14 分别为修正后节点1 与相应节点的逻辑时间差值。而上一轮修正后的理论差值e12、e13、e14 不一定等于本轮测量的实际时钟差值e2、e3、e4，其原因在于通信延迟的存在。具体修正过程如图3 所示。

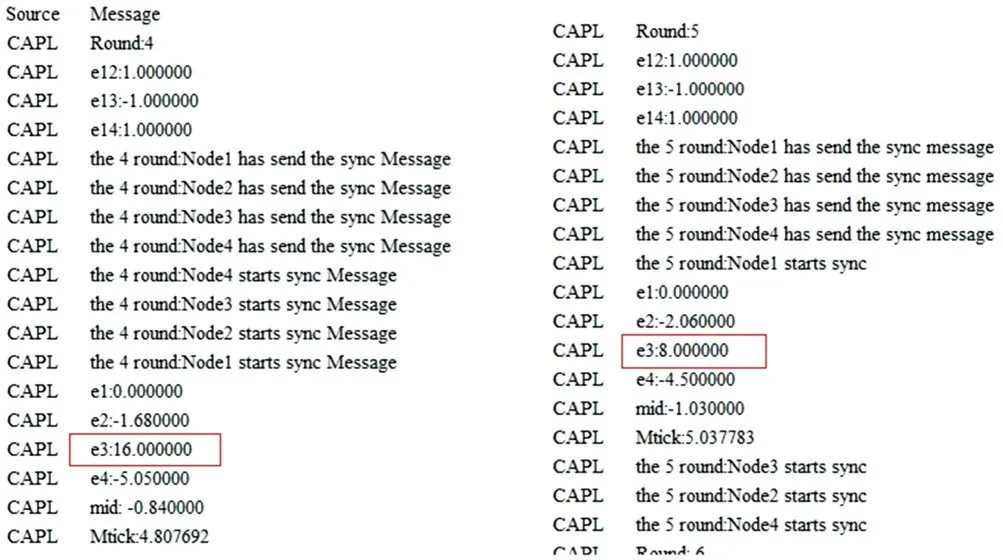
Fig.3 Fault-Tolerant Median（FTM）algorithm correction process图3 容错中值算法（FTM）修正过程

详细结果如图4（彩图扫OSID 码可见，下同）所示，其中两条红线分别为以微秒和逻辑时钟个数为单位表示的FTM 容错中值算法理论精密度。

Fig.4 Fault-Tolerant Median（FTM）algorithm result图4 容错中值算法（FTM）结果

蓝色三角实线表示仿真实验过程中，每轮同步节点1与其它节点逻辑时钟差值的最大值，单位为微秒；黑色三角虚线表示理论逻辑时钟差值最大值与实验逻辑时钟差值最大值的残差，单位是微秒；蓝色圆点实线表示仿真实验过程中每轮同步节点1 与其它节点逻辑时钟差值的最大值，单位为逻辑时钟的个数；黑色圆点虚线表示理论逻辑时钟差值最大值与实验逻辑时钟差值最大值的残差，单位为逻辑时钟的个数。

2.4 基于LL 模型的容错最值算法仿真结果

同理，根前述配置搭建系统并运行，在注入容错最值时钟同步算法到系统中之后，系统节点的逻辑时钟在任一时间段内的修正过程如图5 所示。

Fig.5 Fault-tolerant maximum value clock synchronization algorithm correction process图5 容错最值时钟同步算法修正过程

其中e1、e2、e3、e4 表示节点1 计算的与相应节点的逻辑时钟差值，而Maxv 为据此得出的最大值，Mtick为修正后的单位宏时隙长度，其中节点3 为拜占庭故障节点，故e3 的值为随机值。e12、e13、e14 分别为修正后节点1 与相应节点的逻辑时间差值。而上一轮修正后理论上的差值e12、e13、e14 不一定等于本轮测量的实际时钟差值e2、e3、e4，原因在于通信延迟的存在。

详细结果如图6 所示，其中两条红线分别为以微秒和逻辑时钟个数为单位表示的FTM 容错中值算法理论精密度。蓝色三角实线表示仿真实验过程中每轮同步节点1 与其它节点逻辑时钟差值的最大值，单位为微秒；黑色三角虚线表示理论逻辑时钟差值最大值与实验逻辑时钟差值最大值的残差，单位是微秒；蓝色圆点实线表示仿真实验过程中，每轮同步节点1 与其它节点逻辑时钟差值的最大值，单位为逻辑时钟的个数；黑色圆点虚线表示理论逻辑时钟差值最大值与实验差值最大值的残差，单位为逻辑时钟的个数。

2.5 仿真结果分析

（1）根据容错中值时钟同步算法的结果图可知，本实验所搭建的系统模型满足LL 模型的基本条件，其实验结果完全符合理论结论。容错中值时钟同步算法的结果图符合本文提出的容错最值时钟同步算法理论结果，从实验上证明了本算法的有效性与正确性。

（2）根据容错中值时钟同步算法（FTM）修正过程图与容错最值时钟同步算法修正过程图可知，容错最值时钟同步算法的修正过程相比容错中值时钟同步算法更为激进，其修正效果更为明显。同时根据结果图可知其后果就是精密度的下降。

Fig.6 Fault-tolerant maximum value clock synchronization algorithm results图6 容错最值时钟同步算法结果

（3）根据实验数据分析发现本文的实验数据均为整数，究其原因是因为本文实验计算的结果以逻辑时钟为单位来表示，因此其最小粒度就是单位逻辑时钟长度，初始设为4μs。而逻辑时钟则是用软件的定时器进行模拟，而软件定时器用到的最小粒度同样是整数。由于同一实时时刻不同节点间的时间差就是单位逻辑时钟长度乘以逻辑时间差值，而单位逻辑时间长度与逻辑时间差都为整数，因此差值也以整数的形式呈现。如果从绝对的完美和严谨出发，由于仿真工具及仿真限制的原因，实验数据结果相当于省去了小数部分，因此并不完全精确。但即便对数据进行向上取整处理，结果仍表明系统中非故障节点的逻辑时钟差值最大值低于理论精密度，因此该数据仍能证明本算法及观点的正确性，并不影响得出的结论。

3 结语

本文针对时间触发分布式系统中的时钟同步问题，提出了容错最值算法。基于专业的现场总线仿真测试工具CANoe 软件进行仿真测试，结果表明，容错最值算法能有效地同步系统中的故障节点，包括恶劣情况下的拜占庭故障。通过对既往的FTM 算法和本文的容错最值算法比较可以看出，容错最值算法的修正效果更为明显，但代价是同步后的精确度有所下降。本文提供了一种新的思路，使在不同场景下进行分布式系统的设计者能够多一种选择。