多尺度GTWR城市住宅价格建模与分析

叶 健，胡 鑫，徐鸿蒙，陈 曦，吕 琦

西南交通大学地球科学与环境工程学院，四川 成都 611756

空间位置和时间是城市住宅价格时空变化建模中的决定因素[1]。文献[2]认为“尺度可能是地理信息科学中最重要的课题”；文献[3]同样认为，“尺度几乎是所有地理调查的内在因素”，因此，尺度问题是住宅价格时空关系建模中不得不考虑的问题。

由于地理加权回归(geographically weighted regression,GWR)方法可通过建立空间范围内每个点处的局部回归方程，来探索研究对象在某一尺度下响应变量和一组协变量之间关系，近年来在住宅价格驱动因素建模分析方面受到广泛关注[4]。然而，从住宅价格建模的角度来看，市场趋势、通货膨胀等时间效应的作用对于住宅价格的影响不可忽略。文献[1]将时间维融入GWR技术，提出了时空地理加权回归(geographically and temporally weighted regression,GTWR)分析技术并应用到住宅价格时空关系建模中。近年来，GTWR一直被不断地创新和演化[5]，时空地理加权自回归模型[6]和基于局部多项式[7]求解的GTWR等分析方法相继被提出。

尺度的概念是地理学中的一个重要问题[2,8]，空间和时空现象本质上受尺度效应的影响[9]，空间上可分为全局尺度与局部尺度，时间上可分为长期尺度与短期尺度。混合GWR(mixed GWR)[10-11]将模型参数分为全局和局部两种尺度特征，利用后向迭代算法对模型进行估计。尽管混合GWR能够对GWR模型参数估计尺度进行差异化呈现，参与局部估计的参数对应同样的尺度特征，区分仍然相对单一，缺乏对细节差异的精准呈现[12]。文献[13]提出了MGWR(multiscale geographically weighted regression)，为模型中的每个关系产生单独的优化带宽，从而指示不同关系如何在不同空间尺度上操作，并产生更精确的局部参数估计。多尺度GTWR(multiscale geographically and temporally weighted regression)方法的提出[14]不仅考虑了位置和时间而且充分考虑了多尺度在住宅价格时空关系建模中的作用。

空间距离度量方法的不同会对空间分析模型产生重要的影响[15-16]。欧氏距离易于实现常被作为空间距离的度量方法[17]，但路网距离[18]在测量空间可达性方面常常被认为更有效[19]，因此在计量空间距离时，路网距离通常被认为比欧氏距离更具合理性[20]，然而在路网密集的城市地区，欧氏距离仍被认为可代替路网出行距离[21]。由于城市路网密集程度以及模型的稳定性仍是多尺度GTWR模型稳定发挥的重要因素，因此多尺度GTWR模型不仅需要欧氏距离检测，更需要路网距离的进一步检测。为了完成模型的正确性和通用性的检测，需检测在不同空间距离度量方法约束下，多尺度GTWR模型对于城市住宅价格的实际影响作用，以满足城市住宅价格的实际建模需求。

本文在考虑位置和时间因素的基础上，将多尺度及其路网距离(非欧氏距离)等因素运用到住宅价格时空关系模型建模中，以路网较为密集的成都市为例，构建多尺度GTWR模型，对比欧氏距离约束和路网距离约束条件下典型POI影响因素对城市住宅价格的实际影响，为城市规划提供有价值的分析与判断，同时也为城市规划领域在时空多尺度建模方面提供重要的参考。

1 研究方法

为了辨别时空数据中的异质性，文献[1]将GWR模型[22]扩展到GTWR，模型描述为

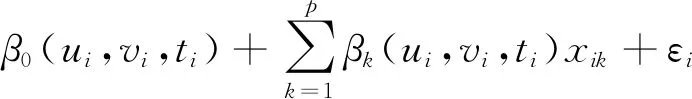
i=1,2,…,n

(1)

式中，xik是位于位置(ui,vi,ti)的第k个自变量；βk(ui,vi,ti)是位置(ui,vi,ti)处基于单一空间带宽和时间带宽的第k个系数；εi是误差项；yi是因变量。GTWR模型中空间权重的计算采用了时空距离与时空带宽的概念，例如高斯空间权重函数在GTWR模型中形式为

(2)

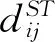
GTWR模型拥有拟合时空异质性的能力，但是GTWR限制了模型内的每个局部关系在单一尺度下进行变化。为了解决空间尺度效应问题，本文采用多尺度GTWR模型，将GTWR模型扩展到不同时空尺度，为每一个自变量提供了独有的时空带宽。其表达式为

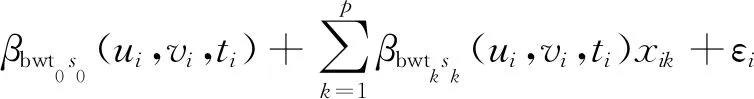
i=1,2,…,n

(3)

式中，xik是位于位置(ui,vi,ti)的第k个自变量；βbwtksk(ui,vi,ti)表示位置(ui,vi,ti)处基于特定空间带宽bwsk和时间带宽bwtk的第k个自变量的估计系数；εi是误差项；yi是因变量。

2 多尺度GTWR模型实现与试验分析

2.1 模型实现

与单一最优带宽的求解方法有所不同，单一带宽求解仅需要将所有参数一起校准，但这样可能会导致强烈的参数干扰和沉重的计算负担[23]。多尺度GTWR模型的实现需要求解各自变量带宽，后向拟合算法[24]能够很好地解决这一问题。该算法是一个迭代过程，主要用于拟合广义可加模型[25]，其基本思想是假设所有其他项都已知，用更平滑的方式校准模型中的每个项。其中，多尺度GTWR中的βbwtksk(ui,vi,ti)xik被定义为第k个加法项fk，从而可以将多尺度GTWR模型表示为

(4)

(1) 首先，使用GTWR回归模型对参数进行初始化，计算局部参数，以此获得所有加项fk的初始估计值，并计算残差ε。

(2) 残差项ε加上第1项f1的当前值作为新的因变量y，x1作为自变量，使用GTWR回归，这将为自变量x1选择出最优的时空带宽bw1，并为该模型生成了新的估计参数β，以此更新f1的值，并使用更新后的f1计算新的残差ε。

(3) 同样，将残差ε加上f2，在x2上使用GTWR回归，以生成时空带宽bw2，并更新f2。直到最后一个加项fm完成更新，以此来完成一次迭代。

(4) 计算COS-CAT，COS-CAT由式(5)可得，根据COS-CAT的大小决定是否终止迭代，否则跳转至第2步

(5)

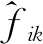
算法：多尺度GTWR后向拟合算法

输入：带有时空位置信息的样本数据(y,x1,x2,…,xm)

输出：多尺度GTWR模型拟合结果，包括模型整体拟合信息R2、AIC值，以及各变量最佳时间、空间带宽和估计参数β值等

(1) 利用GTWR模型初始化各加项fk

(2) do

k←1

whilek≤mdo

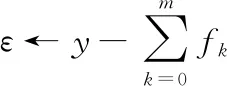
通过GTWR建立e+fk与xk的回归关系，计算xk的最佳带宽

计算AIC和参数β的值，利用新的估计更新fk的值

k++

end

计算COSCAT的值

while COSCAT<10-5

(3) 输出拟合结果

多尺度GTWR模型通过后向拟合算法，单独对每一项自变量带宽进行校准，为模型中的每个自变量与因变量的映射关系产生独有的优化时空带宽，通过迭代不断地对每一个加项fk进行更新，直到fk的变化程度小到达到迭代标准，以此来较为精确地拟合自变量与因变量间的模型，从而达到缩小残差的效果，直观展示不同映射关系如何在不同时空尺度上获取不同的优化时空带宽。

2.2 试验分析

2.2.1 数据准备

模拟试验的时空布局被设计为10×10×10的规则立方体，(ui,vi,ti)为样本点的时空坐标，通过循环遍历区间[0,9]内的所有整数值。根据式(6)设计了模拟数据

yi=β1(ui,vi,ti)+β2(ui,vi,ti)xi2+

β3(ui,vi,ti)xi3+εi

(6)

式中，xi2、xi3的值是从正态分布N(0,2)中随机产生的，误差项εi是从正态分布N(0,0.2)中产生的。

模拟测试中，不同的自变量拥有不同时空异质性的β参数，参数表达式为

(7)

2.2.2 模拟结果

本次模拟设计中，获得了GTWR与多尺度GTWR的最佳带宽(表1)。从表1可以看出，多尺度GTWR正确地识别了局部参数变化的3个不同尺度：β1的最佳带宽比较大，识别了全局这一尺度；而β2和β3的最佳带宽相对较小，表示更局部的尺度。同时，多尺度GTWR模型的AIC(Akaike information criterion)值与RSS值均小于GTWR模型，R平方值高于GTWR模型，表明多尺度GTWR模型的拟合度优于GTWR。

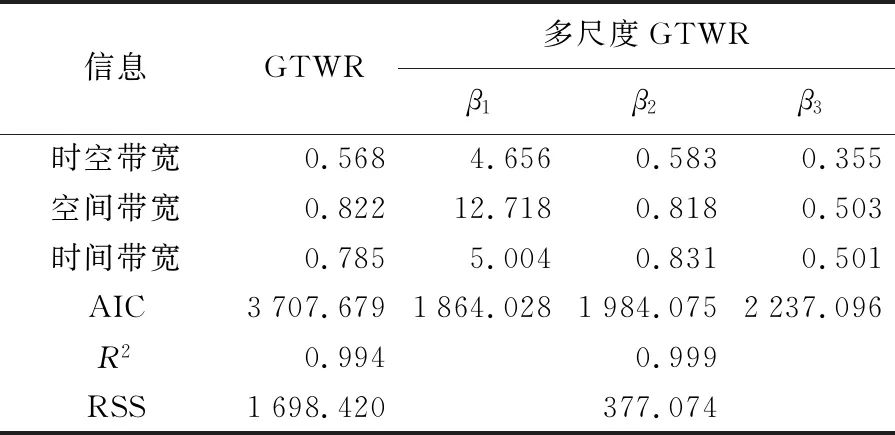
表1 多尺度GTWR模拟测试结果Tab.1 The result of multiscale GTWR simulation test

GTWR和多尺度GTWR复制已知参数面的能力由系数βj的均方根误差(RMSE)来估量，较小的RMSE值表示对已知局部参数集的更准确复制。如图1(a)所示，多尺度GTWR比GTWR更精确地拟合了3个参数，尤其是对β1、β2参数的复制。图1(b)进一步表明，多尺度GTWR模型参数面的复制情况优于GTWR模型。多尺度GTWR可以较为精确地复制所有3个参数面，而GTWR在复制β1、β2时出现了明显的形变。

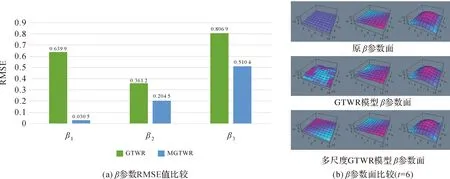
图1 GTWR和多尺度GTWR模型β参数结果对比Fig.1 Comparison of β parameter results between GTWR model and multiscale GTWR model

3 研究区域与数据源

本文以成都主城区为主要研究区域，包括锦江区、武侯区、成华区、金牛区、青羊区、高新西区、高新南区、龙泉驿区、新都区、郫都区、双流区、温江区等，研究区域内住宅价格的时空分布格局以及各类影响住宅价格的相关因素。

研究区域内有关住宅价格的数据均来自链家网(https:∥www.lianjia.com/)，以成都市出售的新房或二手房单位面积成交均价作为住宅价格数据源，采集2015年至2018年共1641条住宅价格数据，具体信息如图2所示。

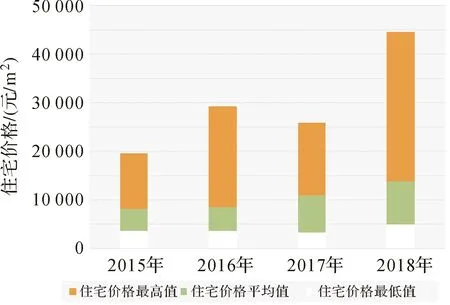
图2 住宅价格数据统计特征Fig.2 Statistical characteristics of housing price data

各类特征点数据由成都市门户网站获取，包括公立中小学、公立三甲医院、五星级酒店、大型商场、地铁站点、成都火车站、双流机场、旅游景点、中心商务区，并随住宅价格点数据一同录入到ArcMap中。

地理加权回归分析常采用欧氏距离作为度量空间距离的标准，欧氏距离反映了数据点之间的最短距离，但城市间的空间距离不能简单等同于直线距离，使用路网距离更能代表表示城市OD空间距离。如图3所示，路网距离是基于交通网络的最短路径距离。为了验证路网距离约束在表达空间距离时的准确性，本文研究分别采用欧氏距离和路网距离，通过GTWR和多尺度GTWR试验分析验证。

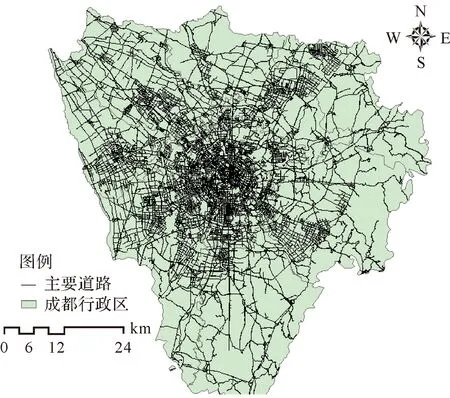
图3 成都市道路网Fig.3 Road network of Chengdu

路网距离由ArcMap的network analyst模块进行解算，在模块中分别计算成都市住宅价格点的空间距离矩阵，以及住宅价格点与各类POI点基于路网的最短距离(表2)，并将结果作为字段保存到住宅价格点的属性表中。

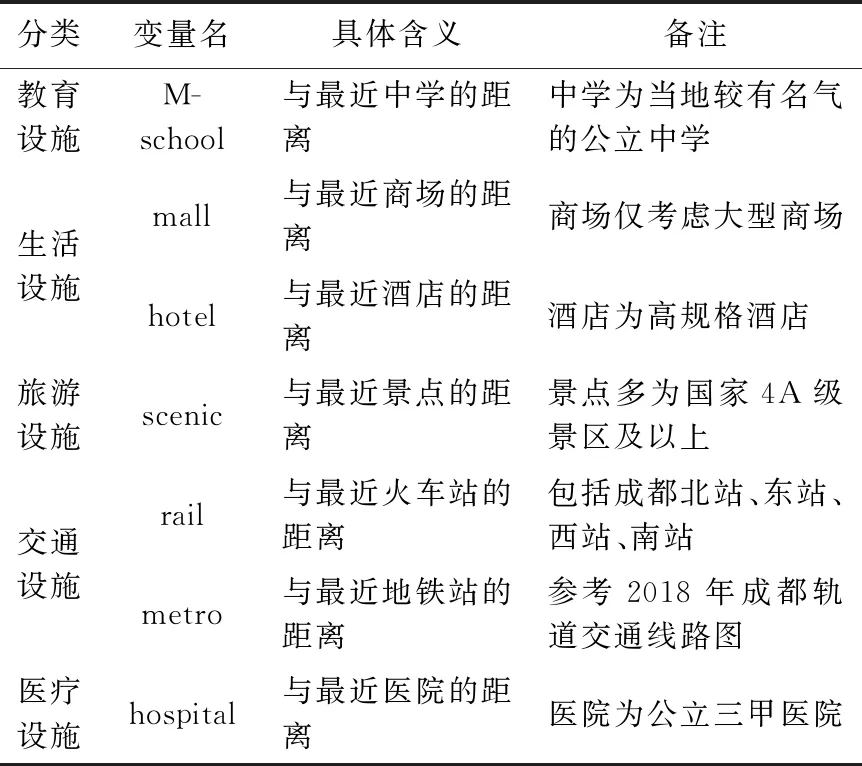
表2 变量含义说明Tab.2 Definition of variable

数据中多重共线性的存在会对地理加权回归分析的结果产生较大影响，必须排除数据中的多重共线性，本文使用方差膨胀系数(VIF)作为判别是否具有多重共线性的标准。由于住宅价格中的部分数据存在明显多重共线性，选择保留公立中学、地铁站点、大型商场、成都火车站、著名景点、公立三甲医院、高规格酒店的最短路网距离数据作为最终的自变量(表3)。可以由表3看出，处理后所有数据的VIF值均小于10。

表3 多重共线性检测Tab.3 Detect multicollinearity

4 结果分析

4.1 城市住宅价格距离度量对比分析

依据成都市住宅价格数据，分别通过路网距离约束和欧氏距离约束构造多尺度GTWR和GTWR模型，通过两者之间的对比来探索不同距离度量标准之间回归模型的不同之处。对比结果见表4。相对于GTWR的结果，多尺度GTWR残差平方和(RSS)、拟合优度(R2)得到明显的改善。

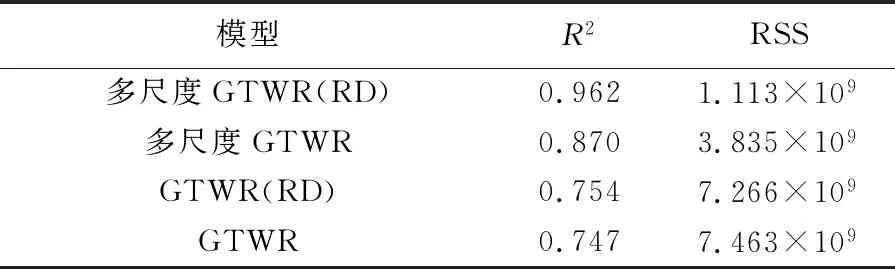
表4 拟合结果Tab.4 The result of goodness-of-fit

同时，使用路网距离作为度量标准也有效地改善了模型的拟合效果。结果表明，相较使用欧氏距离约束的GTWR与多尺度GTWR模型，路网距离约束的GTWR(RD)模型的拟合优度提高了0.007，多尺度GTWR(RD)模型的拟合优度提高了0.092，并且GTWR(RD)模型残差平方和降低了1.97×108，多尺度GTWR(RD)模型残差平方和降低了2.722×109。

图4展示了4个模型中不同变量的AIC值。试验结果显示，在同一距离约束下，多尺度GTWR模型相较GTWR模型， 可以有效降低所有变量的AIC值，表明多尺度GTWR对各个变量更具有解释性。同样，在同一模型下，使用路网距离约束相较使用欧氏距离约束也能降低各变量AIC值。这说明在路网密集的成都市，尽管欧氏距离能够基本满足多尺度GTWR城市住宅价格建模需求，但路网距离更能反映成都市中心城区空间距离，且能够有效地增加模型的解释能力。

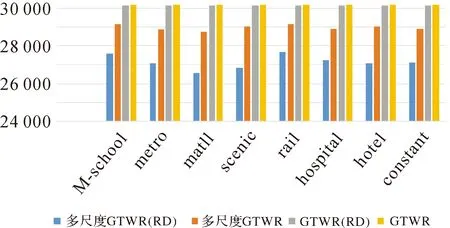
图4 不同模型下AIC值的对比Fig.4 Comparison of AIC values under different models

4.2 GTWR与多尺度GTWR模型对比分析

基于路网距离约束，得到GTWR(RD)模型以及多尺度GTWR(RD)模型的拟合结果(表5、表6)。对于多尺度GTWR(RD)来说，所有空间带宽介于0.34 km和10.13 km之间，时间带宽介于0.23季度与12.51季度之间，对于GTWR(RD)，空间和时间带宽分别为2.30 km和2.10季度，可以看作多尺度GTWR模型带宽进行加权平均的结果。说明多尺度GTWR可以有效地测量和识别时空关系的尺度，这些不同尺度代表了时空异质性。

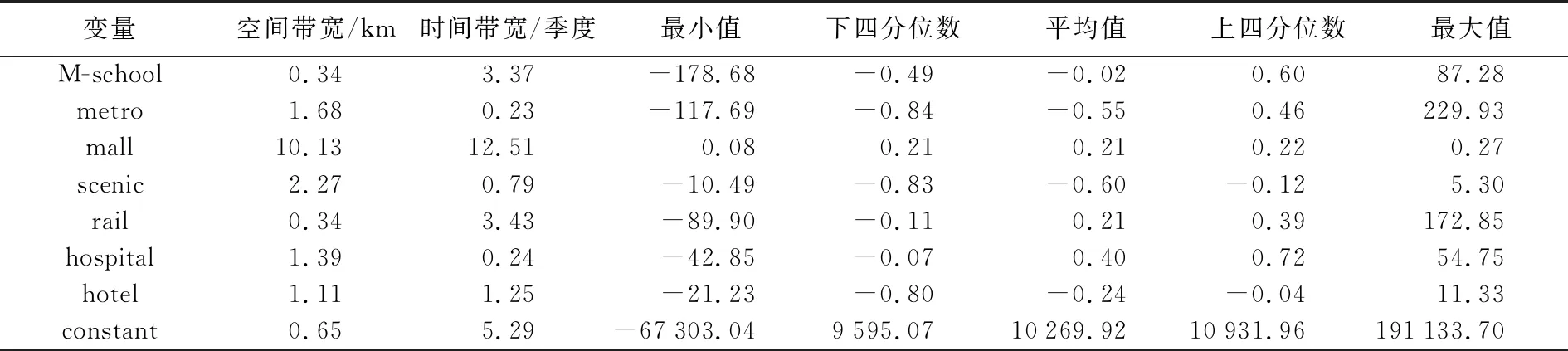
表6 多尺度GTWR(RD)结果Tab.6 The result of multiscale GTWR(RD)

分析每个变量的带宽，可以看出，商场的空间带宽与时间带宽分别为10.13 km和12.51季度，均大于GTWR的时间带宽与空间带宽结果，并且与本项目所研究的时空范围最接近(空间范围约为30 km×30 km，时间范围为2015至2018年16个季度)。空间带宽与时间带宽过大表明变量没有明显的空间与时间异质性，说明商场对住宅价格的影响在空间与时间上是全局的。

与此相反，地铁、景点、医院、酒店这4个变量的时间带宽、空间带宽均小于GTWR中的结果，表明这些变量在更小的尺度上影响成都市住宅价格的趋势。同时，中学、火车站的空间带宽小于GTWR中的空间带宽，而其时间带宽却大于GTWR中的时间带宽，说明不同的变量，其时间异质性与空间异质性水平也有所不同。

4.3 多尺度GTWR模型结果分析

4.3.1 分析时间维中估计系数的变化

如图5所示，在2015—2018年16个季度内，变量scenic、hotel的估计系数可视为负，即距离此类POI点越远，住宅价格越表现出更低的价格。热门旅游景区资源以及高规格酒店一直是影响住宅价格的重要因素，考虑到旅游带来的经济效应，购房者会倾向于投资靠近景区的住宅。同样的，高规格的酒店也会带动周边的商业，但影响程度不如热门景区资源大。

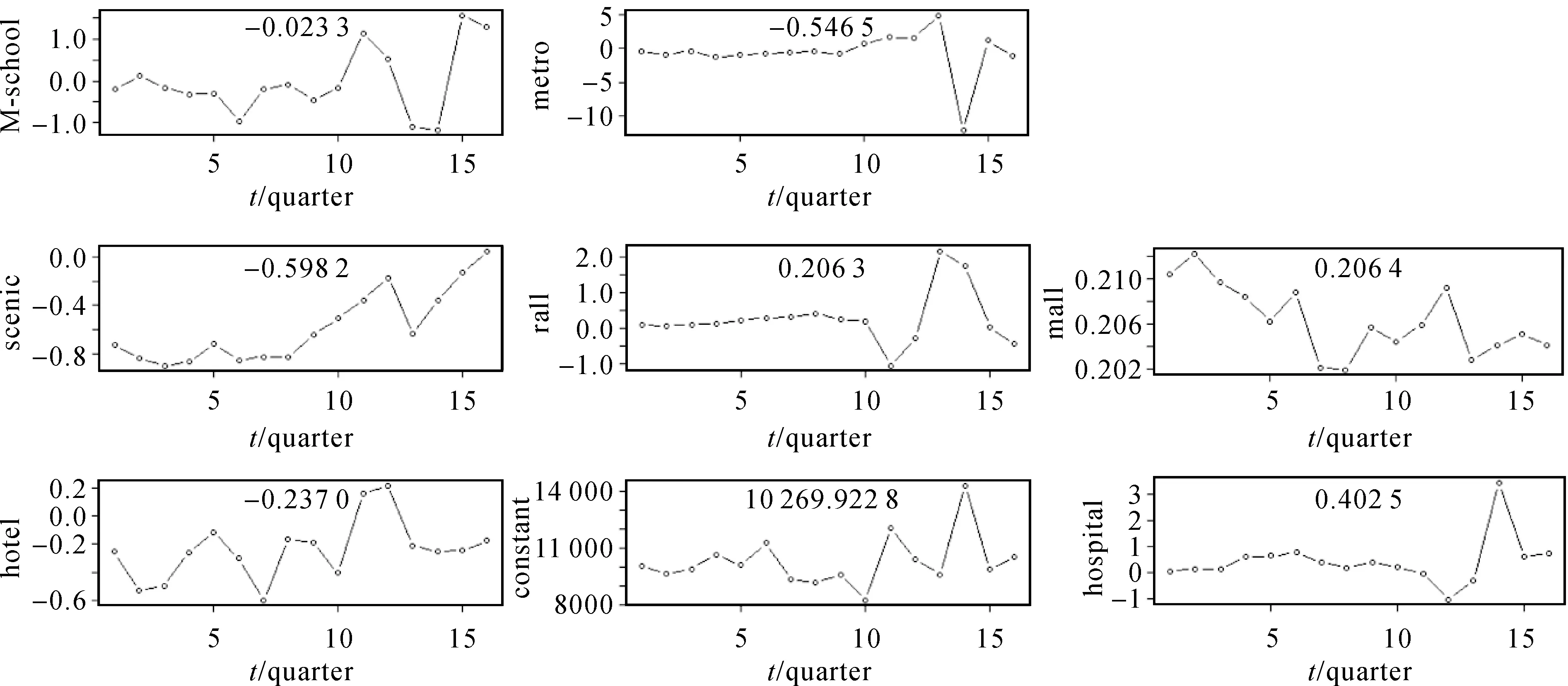
图5 各变量估计系数的时间变化(数值为全时期估计系数平均值)Fig.5 Time variation of estimated coefficients for each variable (data are the average value of estimated coefficients for the whole period)

变量M-school、metro的估计系数整体上表现为负值。一般来说，购房者会倾向于购买高交通便捷度以及附近拥有教育设施的住宅。变量metro在第14季度有明显的波动，可能是受地铁1号线三期开通的影响。地铁1号线三期是深入天府新区核心区的首条地铁线路，1号线三期的开通连接了中心城区和天府新区核心区，对住宅价格造成较大影响。

变量rail、hospital以及mall的估计系数起伏不定，在不同时间段对住宅价格表现出不同的影响作用，但最终表现为正值。分析可知，此类特征点会导致周边宜居程度降低，居民会倾向于购买其他宜居程度高的住宅。

4.3.2 分析空间维中估计系数的变化

图6以2018年下半年中变量mall与metro为例分析估计系数在空间维中的变化。图6(a)展示了变量mall估计系数在空间位置中的分布，变量mall仍然展示了其全局性，估计系数在空间中并未出现较大差异，整体维持在0.08至0.26这一范围内，并大致由西向东缓慢增加，说明成都市以东的区域住宅价格受商场分布的影响更大。

图6(b)展示了变量metro估计系数在空间位置中的分布，可以看出，相对于mall而言，变量metro在空间维度上表现出较为显著的空间异质性，估计系数的波动较大，metro系数为正的区域主要位于成都东北端，系数为负的区域主要位于南端以及西北端，而在城市中心区域则表现出正负系数相互嵌套的现象。说明地铁站点在成都市大部分区域对住宅价格起着促进增长的作用，在东北端则表现出对住宅价格的消极影响。可能由于政府地铁规划部分主要在中南端，导致了此区域系数估计值的异常。

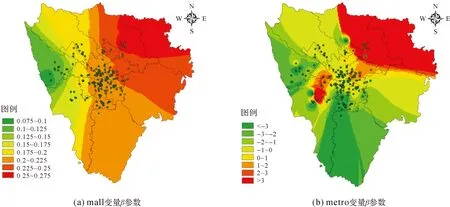
图6 mall和metro估计系数的空间变化(2018年下半年)Fig.6 Spatial variation of mall and metro estimated coefficients (second half of 2018)

5 结论与讨论

传统的GWR模型只能对空间异质性进行量化，缺少对时间维度的刻画，并不具备识别独立关系的能力。GTWR模型将GWR模型拓展至时间维度，但仍然缺乏探索多尺度效应的能力。本文将多尺度和时间维同时扩展到城市住宅价格的建模中，展示了如何使用多尺度GTWR来识别和测量不同过程操作的不同时空尺度。另外，由于空间距离一直是制约地理时空加权回归模型求解精度的关键，本文以路网较为密集的成都市为案例区域，分别基于欧氏距离约束和路网距离约束，获取模型的拟合优度，确定不同空间距离约束下模型的正确性和通用性。

在基于多尺度GTWR住宅价格建模方面，多尺度GTWR的建模精度优于不考虑多尺度时空非平稳性的GTWR，多尺度GTWR中残差平方和(RSS)、拟合优度(R2)得到了明显的改善，表明模型较好地拟合了整体数据，对各解释变量具有更好的解释作用。

通过充分对比路网距离和欧氏距离对成都市住宅价格模型建模的影响以后研究发现，GTWR和多尺度GTWR利用路网距离测算时空距离均要比欧氏距离建模拟合精度更高，其中GTWR(RD)模型的拟合优度提高了0.007，多尺度GTWR(RD)模型的拟合优度提高了0.092，AIC值明显优化，再次说明了路网距离在测量成都市空间可达性方面更有效。在时空维度分析中，路网约束的多尺度GTWR模型的结果进一步展示了模型的可靠性。结果表明，在多尺度GTWR模型中，路网距离约束相较于欧氏距离约束在成都市空间距离度量方面的表现更具有合理性。

多尺度GTWR不仅可以研究时空过程中的时空异质性，而且可以通过识别不同时空带宽，从而指示不同关系如何在不同时空尺度上操作，因此在解释住宅价格变化方面具有更好的表现。尽管欧氏距离能够基本满足多尺度GTWR城市住宅价格建模需求，但路网距离更能反映成都市中心城区空间距离，能够更有效提升地理时空加权回归模型求解精度，本文全面验证了模型的正确性和通用性。

本文结果能够为城市规划人员促进住房市场发展提供新的观点和启示。近年来，GTWR已逐步扩展到景观动态[26]、社会学[27]和环境保护[28-29]等领域，本文提出的建模方法及其应用具有很好的前景和应用价值。