面向地理路网的交通信号智能协同控制方法

郑 晔，郭仁忠，马 丁，赵志刚，李晓明

1. 深圳大学建筑与城市规划学院智慧城市研究院，广东 深圳 518060； 2. 深圳市空间信息智能感知与服务重点实验室，广东 深圳 518060

随着我国小汽车持有量的不断增加，交通拥堵逐渐成为城市管理最为棘手的问题之一。城市路网承担了整个城市的大部分交通运输，通过对路网中的关键路口信号灯配时和相位协调能有效提高交通运行效率，是面向智慧城市建设的关键研究内容[1]。传统路口交通信号配时方法通常有两种实现方式：①将道路空间信息作图后通过测量几何信息实现；②建立数学模型寻找目标函数最优解实现。以绿波协调为例，传统方法利用干道上信号灯之间的距离及汽车的行驶的绿波速度构建混合整型线性规划方程，求使绿波带宽最大的方程解[2-5]。上述方法具有以下局限性：①所有车辆都必须以相同速度进行行驶(即绿波速度)，一旦有少数车辆与绿波速度差距较大，将破坏整个队列导致绿波效果差；②传统方法需要发车规律维持相对稳定的速度，如果车流变化大会使计算绿波效果降低。

计算机技术的发展促进诸如模糊逻辑控制[6]、遗传算法[7]、专家系统[8]等机器学习算法引入智能交通领域。在众多机器学习算法中，深度强化学习(deep reinforcement learning，DRL)基于马尔可夫决策理论令智能体在环境中不断做出相应的决策，并对其行为决策进行回报反馈，使智能体在环境中寻找回报值最高的序列决策[9]。智慧交通信号控制系统通过对交通场景中行为向量、状态向量和回报函数的定义，实现交通信号灯的智能化控制[10-12]。随着5G、云计算技术发展，DRL技术在交通管理中有了新的突破。文献[13]提出一种在车联网和5G的环境下，利用DRL构建一个支持能够在云端和边缘端动态调度的交通控制系统。文献[14]提出一种基于边缘计算的DRL流量采集方法，并将此方法应用于缓解交通堵塞问题。文献[15]从智慧城市建设角度设计一套DRL信号控制系统，协同多个路口提高总体交通吞吐量。文献[16]完善了基于DRL信号控制算法的细节，在此算法中智能体的状态向量是划分成网格后的交通流量数据，决策行为函数是交通灯的持续时间变化，回报函数是两个周期之间的累计等待时间差。文献[17]提出的DDPG-BAND算法，通过DRL对城市干道进行绿波协调，实现城市干道多路口协同控制。

总体而言，DRL技术已经较成功地应用于交通信号控制中，但是当前研究一般局限于单路口或者城市干道，基于地理路网多智能体的交通信号协同控制较少。本文结合城市地理路网特征和强化学习特点，提出一种基于强化学习的双层信号协同控制训练方法，并将此方法应用于宁波市某中学片区路网。通过与传统配时方法在仿真器中的旅行时间、吞吐量和停车次数上的比较，证明了本文方法的可行性和有效性。

1 本文方法

1.1 马尔可夫决策过程

强化学习主要研究智能体不断地在动态环境中进行试错和反馈训练，从而智能体能在变化环境中获得最大累积回报的序列决策[18]。强化学习理论基础是马尔可夫决策过程(Markov decision process,MDP)，包含3个基本单元状态向量(也称观察向量)S，决策向量A和回报函数R[19]。智能体在执行决策行为后与环境交互，其状态由S1转移至S2，状态转移矩阵记为P。在执行序列决策过程中，当前决策比历史决策影响更大，假设决策的衰退率为Y(γ∈[0，1])，则上述MDP用式(1)表示

MDP=〈S,A,R,P,Y〉

(1)

在MDP问题中，智能体不同状态下做出决策行为不一样，策略函数表示在当前状态下智能体执行多个候选决策的可能，其输入参数为当前状态s(s∈S)和决策向量a(a∈A)，其输出结果为每一候选决策的可能。令π表示策略函数，则π(s,a)表示在智能体在状态s条件下，执行策略a的概率。如果智能体按照策略函数π进行MDP，在第t次执行决策的回报值为Rt，其状态从st转移至st+1并获得回报值rt的过程表示为

rt=P(si,π(si))

(2)

MDP的回报总和表示为

(3)

由上述公式得出，不同策略函数会导致智能体执行不同行为策略的概率不一样，而不同行为策略所产生的回报值也不一样，强化学习的策略函数满足整个序列决策的总回报值最大。优秀的策略函数不仅仅满足当前决策能够取得最大回报值，更能保证整个序列决策过程的总体回报总和最大化。由于智能体策略函数π(s,a)是状态的概率转移过程，状态动作值函数Qπ(s,a)表示智能体在状态的s初始条件下，按照按策略函数π序列决策所得回报的数学期望，即表达为

(4)

因此，MDP问题本质是寻找最优的策略函数π，使得智能体从任意状态S′开始的决策行为能满足状态动作价值函数Qπ(s,a)取得最大值。根据贝尔曼方程[20]，第t次决策的状态动作价值函数的仅于第t-1次决策的状态动作价值函数有关，因此状态动作价值函数可简化为

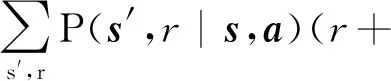
Ymax(Qπ(st-1,at-1)))

(5)

在深度强化学习中[21]，智能体将状态动作值存入以s和a为索引的深度神经网络中，通过从不断的与环境交互并得到回报函数反馈更新神经网络，最终能使神经网络中存储的状态动作值能正确指导智能体在环境中执行回报值最高的序列决策。

1.2 基于MDP的地理路网交通场景设定

本文通过智能体改变信号灯各相位的绿灯时长来达到交通协调目的，场景设定如下：

(1) 信号灯绿灯配时、相位差由智能体智能决策决定。

(2) 智能体不改变信号灯的相序。

(3) 信号灯的黄灯时长为固定2 s。

基于上述预设条件，本文方法分为两层(图1)：第1层为工作智能体，其职责对单个路口进行优化，保证每一路口智能体能够调节各自路口的绿灯时长，使其不造成交通堵塞。第2层为管理智能体，其职责是协调各个工作智能体，提高地理路网整体交通效率。

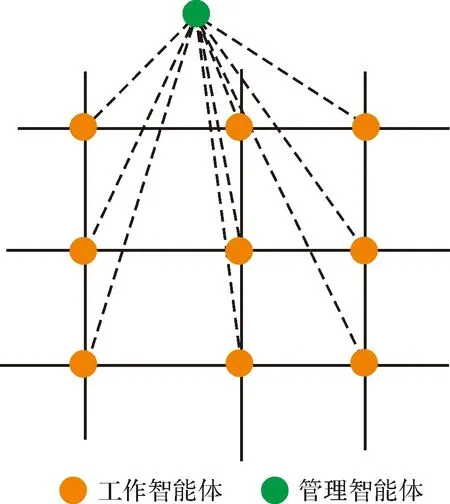
图1 双层协同优化策略Fig.1 Two-tier collaborative optimization strategy

通过将地理路网中地理路网交通场景各个变量特征提取后代入贝尔曼方程，经过训练后可以实现智能体对交通信号灯的自动调控。在下文中将着重描述如何在上述两层智能体中定义MDP中的状态向量、决策向量和回报函数。

1.3 单路口工作智能体设定策略

1.3.1 工作智能体的状态向量S

地理路网交通场景中，工作智能体的状态向量必须能够反映当前路口的交通阻塞状态。如图2所示，排队长度表示交通路口中等待红灯变绿车辆的总数。在单路口中，车辆排队长度反应路口各个方向的车流量，是决定对应相位绿灯时长的关键因素。除了排队长度外，由于车辆重量和长度直接决定了车辆的启动速度和车辆在转弯过程中耗费时间。因此，本文区分两种类型的交通车辆作为状态向量的加权值，一类为重量超过15 t或长度大于12 m的大型车(如泥头车或公交车)，另一类是普通的小客车。

通过上述加权后排队长度，定义两种粒度状态向量：①粗粒度的状态向量只计算每一方向道路上的加权排队长度总和，以图2为例，粗粒度的状态向量的维度为4,每个维度的值为每一方向的车辆加权后总和；②细粒度的状态向量维度则为8,每一维度为每一车道的车辆加权后总和。

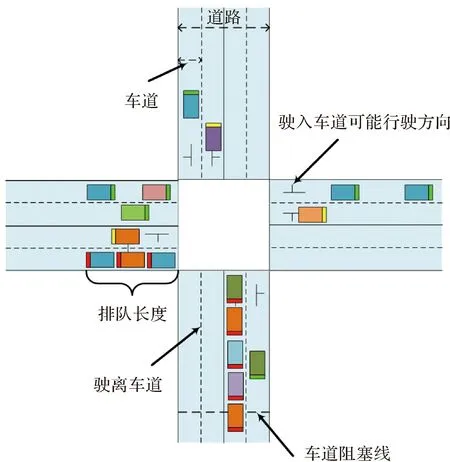
注：长方形表示行驶车辆，车辆尾部的颜色代表不同的车辆行驶状态，绿色代表车辆正常行驶，黄色代表车辆正在减速，红色代表车辆正在停止等待红灯。图2 道路交叉口[17]Fig.2 Traffic crossroads[17]

1.3.2 工作智能体的决策向量A

由MDP理论可得，策略函数π根据状态向量S和决策向A计算智能体下一步决策，因此需要定义工作智能体在地理路网下的决策向量A。智能体改变信号灯各相位的放行时间来达到交通协调目的，工作智能体的决策向量为保存信号灯每一相位的绿灯时长的高维数组。本文中，单路口工作智能体的决策向量A应满足以下条件：

(1) 决策向量每一维度的数值是正整数(一般信号灯绿灯时长没有小数)。

(2) 决策向量每一维度的数值必须大于某一固定最小值(信号周期表示信号灯从绿变红，再变绿的整个时间长度，为了确保行人能以正常速度通过，其必须大于某一与路口宽度有关的固定值)。

(3) 决策向量所有维度数值之和必须小于某一固定最大值(信号灯周期表示不能超过一般人能忍受的范围，比如5 min)。

智能体对信号灯相位进行绿灯配时后，交通仿真器运行一定周期后通过回报函数对智能体的决策进行评价，因此如何正确定义回报函数是本算法的关键。

1.3.3 工作智能体的回报函数R

回报函数R的定义决定智能体策略函数π的优化目标，工作智能体的优化训练后的优化目标为保证每一单个交叉路口不会交通堵塞，因此首先必须对交通阻塞进行量化的定义。如图2所示，车道阻塞线位于道路末端衡量车流是否阻塞的基准线。如果车辆排队长度超过车道阻塞线，则认为该路口已经发生交通拥堵。在一般的场景中，车辆阻塞线与道路末端距离不小于道路长度的20%，即当车辆排队长度不超过车道总长的80%路口该车道方向交通畅通。交通阻塞数表示在一定时间内，所有车道排队长度超过交通阻塞线的次数总和，是工作智能体交通调控优劣的依据。基于上述定义，回报函数设置如下：

(1) 如果调控交通前阻塞数为0，调控后交通阻塞数大于0，表明调控后使交通状况从不堵塞状态转变为阻塞状态，返回回报值-1。

(2) 如果调控交通前阻塞数大于0，调控后交通阻塞数为0，表明调控后使交通状况从堵塞状态转变为不阻塞状态，返回回报值1。

(3) 如果调控前比调控后交通阻塞数减少或增加量超过20%，表明调控效果较为明显，分别返回回报值1和-1。

(4) 其他情况下表明调控效果不明显，不足以判断优劣，返回回报值0。

1.4 管理智能体协同优化策略

工作智能体可以保证各自交叉路口不会交通堵塞，即每一工作智能体的交通阻塞数为0。管理智能体在此基础上进一步对上述工作智能体进行协同控制，保证整个地理路网的交通运行效率最优。管理智能体的状态向量和决策向量与工作智能体类似，其维度是所有工作智能体维度之和，分别代表所有路口排队长度和绿灯配时。因此，本节主要定义管理智能体的回报函数。

管理智能体优化目标的定义必须随着不同场景改变。例如，高峰时期应通过信号协调达到单位时间内路网整体能够通行更多车辆，因此早高峰的优化目标定义为路网整体吞吐量；而低峰期应更多考虑通过信号协调减少路网内车辆平均等待红灯时间。交通效率系数表示指定场景下工作智能体的优化目标(例如，早高峰时交通效率表示单位时间里场景内路口吞吐量总和)，则管理智能体的回报函数定义如下：

(1) 如果调控后使任意路口的交通阻塞数大于0，直接返回回报值-1。

(2) 如果交通效率系数调控前比调控后增加10%，则调控效果优，则返回回报值1。

(3) 如果交通效率系数调控前比调控后减少10%，则调控效果差，则返回回报值-1。

(4) 其他情况调控效果不明显，返回回报值0。

2 试验分析

2.1 试验数据和试验环境介绍

如图3所示，宁波某中学片区位于宁波市鄞州区，是宁波市城区内车流较为密集的地区之一。该路段东起福明路西至桑田路，南起惊驾路北至民安路，由12条地理路网构成的4个信号灯组成。

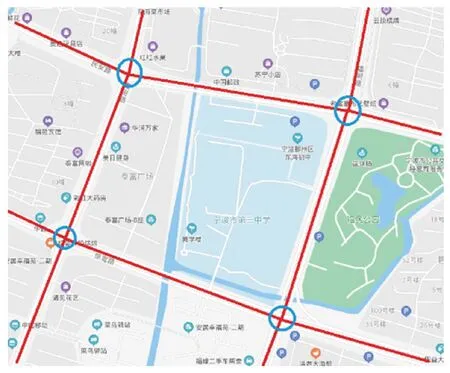
图3 试验区的交通路网Fig.3 Illustration of traffic roads in the experimental area

试验车流数据来源于试验区2020年12月6日7:00AM至9:30AM时间段的路口摄像头，应用目标跟踪算法后取平均得到(表1)。试验数据包括每个路口东、南、西、北4个驶入方位和左、中、右3个驶出方向，并区分了大型客车和小型汽车。

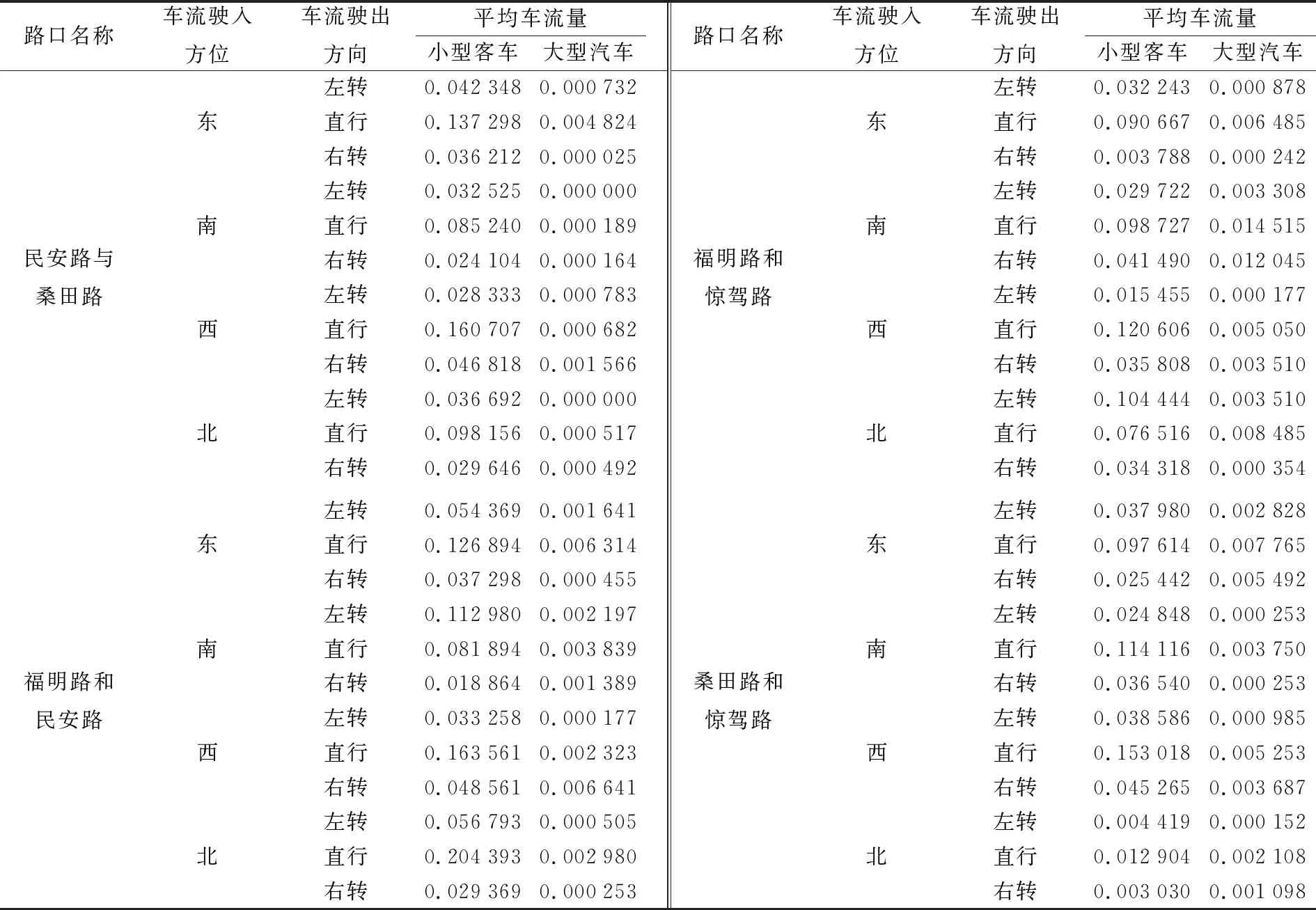
表1 交叉口车流信息Tab.1 The rate of traffic flow in the intersection (辆/s)

本文试验算法部署于24核CPU和 32 GB内存的高性能计算机上，操作系统采用CentOS 7。算法实现于Python 3.7.3，神经网络搭建采用Tensorflow1.14，交通环境运行于仿真软件SUMO 1.3.1[22](由德国航空航天中心运输系统研究所开发的开源软件)。

2.2 试验结果分析

2.2.1 工作智能体训练结果

本节探究粗细两种状态向量下，单路口的工作智能体训练过程。试验中，智能体每间隔两信号周期观察交叉路口中排队长度，并以此产生输入向量更新状态动作值神经网络，模拟时长7200 s为一次迭代。图4表示每一路口工作智能体的交通系数随着迭代次数的，其中纵坐标表示在一次迭代中交通阻塞数的累积总和，横坐标表示迭代次数。试验结果表明，随着迭代次数的增长，4个路口的交通阻塞系数都呈降低趋势；当迭代次数大约至100次时，交通阻塞系数达到收敛。除此之外，粗粒度状态向量下训练的交通阻塞系数稳定性和效果更为优异。这是由于粗粒度状态向量是以边为单位计算排队长度。当每条边上的车辆通行需要通过信号灯多个相位进行控制时，粗粒度状态向量会使无法准确区分究竟哪一相位需要更多绿灯时长，因此其训练也相对难以收敛。

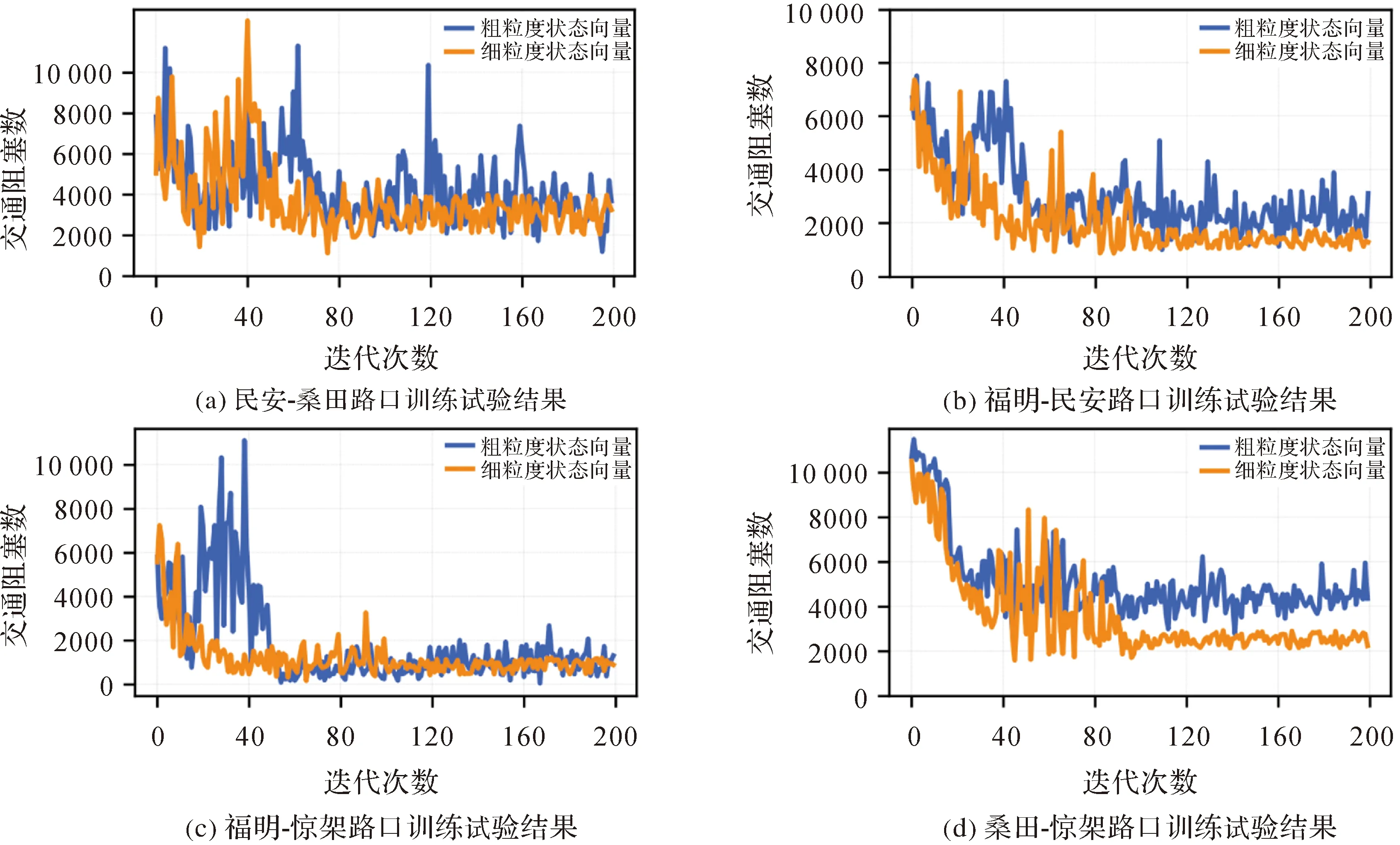
图4 单路口工作智能体训练试验结果Fig.4 Training results of working agent on single intersection

2.2.2 管理智能体训练结果

将2.2.1节训练所得到的工作智能体放入地理路网中，在管理智能体协调下实现地理区域的协同优化训练。本文试验智能体每3个信号周期更新状态动作值神经网络，模拟时长10 800 s为一次迭代。本文试验选取地理路网中车辆平均旅行时间、平均停车次数和吞吐量3个指标作为优化交通效率系数。如图5所示，3项验证指标经过训练后的效率都有所提高(平均旅行时间和停车次数减少，吞吐量增加)，并且当迭代到达一定次数后收敛，说明本方法具有效性。通过计算，最后30次迭代比最初始30次迭代，平均旅行时间减少19.12%，平均吞吐量增加21.47%，平均停车次数减少了3%。

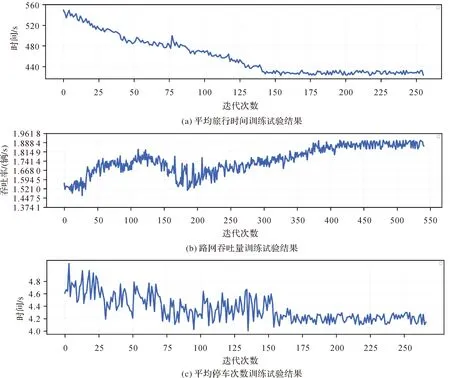
图5 地理路网管理智能体训练试验结果Fig.5 Training results of management agent on geographic road network

2.2.3 交通效率系数对比

为了验证本方法的有效性，本文方法、原始作图方法和经典韦伯斯特方法[23]实现的配时方案在地理路网中的交通效率进行比较。在试验中加入10组随机种子，随机种子能够在指定车流量条件下产生不同发车规律，通过这10组随机种子下的平均路网交通效率能保证试验的公正性。如图6所示，试验以270 s为一轮统计周期，比较3种方法各交通效率系数。结果表明，本文方法平均旅行时间比原始作图方法减少7.03%，比经典韦伯斯特方法减少2.87%；本文方法停车次数比原始作图方法减少12.56%，比经典韦伯斯特方法减少10.49%；吞吐率比原始作图方法提高8.3%，比经典韦伯斯特方法提高6.4%。总体来说，本文方法在车辆平均旅行时间、停车次数和吞吐率上都有较为优异表现。特别在停车次数上，其他两种方法随着周期明显效率开始下降。这是由于传统方法通过数学计算得到固定配时方案，本文算法的智能体能通过每个方向的排队长度实时改变配时，因此具有更好的自适应性。

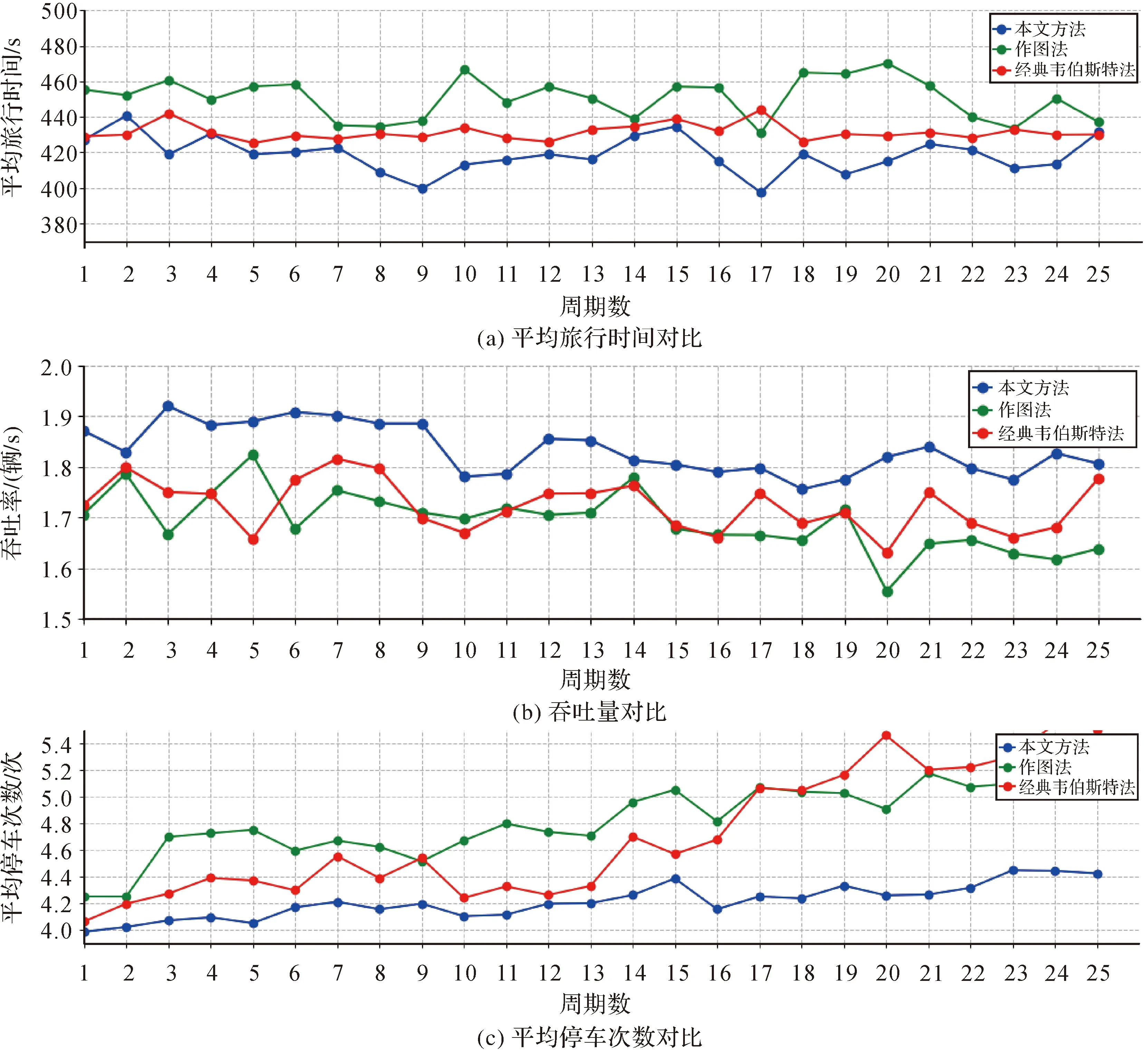
图6 3种交通效率系数对比Fig.6 Comparison of three traffic evaluation indexes

3 结 论

本文结合马尔可夫序列决策特点，提出一种基于强化学习的双层智能体协同控制训练方法。在第1层针对单个路口实现粗调训练，智能体通过观察路口每一车道的排队长度调控信号配时，实现单个路口不堵塞；第2层将多个粗调训练后的智能体模型放入地理网络中，实现多路口的协同微调训练。试验结果表明，与传统算法相比本文方法在旅行时间缩短7.03%，停车次数减少12.56%，吞吐量提高8.3%。另外，基于强化学习实现的交通信号协调控制能够根据路口车道排队长度实时改变配时方案，能够更好地适配于复杂多变的交通环境。