基于IMU及UWB的微型弹跳机器人传感器节点位姿检测研究∗

江朝军倪江生张 军李 汉

(东南大学仪器科学与工程学院，江苏 南京210000)

当今世界，机器人的应用日益广泛，其面临的作业环境愈发恶劣，诸如灾害救援、地质勘测中都期望具备感知能力的机器人替代人员，作为传感器节点，完成信息收集和辅助作业等任务。这类环境往往地形崎岖多变，多障碍物和沟壑地形，相较于传统微型轮式机器人节点，具有更灵活的运动性能的微型弹跳机器人(MJR)节点更能胜任此类任务。

弹跳机器人具有较强的越障能力，但同时也有难以控制以及姿态调节复杂等问题需要解决。目前弹跳机器人从运动形式上分为两类:一类是作连续性弹跳运动[1]，即弹跳腿碰到地面后在很短的时间内再次起跳，弹跳机构的蓄能、姿态调整等都是动态完成的。而另一类作间隙性运动[2－4]，即落地后需要短暂时间用于姿态调整和弹跳机构蓄能等，为后续的弹跳做准备，相对简化了控制。

无论是连续性还是间歇性弹跳运动，要实现长距离运动，都需要进行位姿检测与调节。美国喷气推进实验室(JPL)在弹跳式机器人的研究方面获得较多的成果，其中较出名的是其设计的三代间隙性弹跳式机器人[5－8]。其中文章[8]中提出了一种针对弹跳机器人的融合相机、惯性和加速度数据的定位算法，但仅进行了仿真分析，并未实现样机测试。瑞士联邦理工学院Kovac等人结合蚱蜢的运动方式，研制出一款微型弹跳机器人[9－11]，其利用三轴加速度计检测姿态，并通过笼架结构实现被动式复位设计。密歇根州立大学的赵建国等人受蜥蜴空中操纵能力的启发，开展了微型尾巴跳跃机器人的机构设计与控制研究[12－14]，其利用加速度计检测自由落体，采用陀螺仪检测空中机体角度并加以控制。国内机构在弹跳式机器人方面的研究也在不断深入，并取得了不少成绩。上海交通大学杨煜普教授等人提出了一种翻转跳跃单腿机器人模型[15]。东南大学研制了一款仿蝗虫微型弹跳式机器人，弹跳高度能达到0.8 m左右[2－4]。

弹跳机器人的位姿信息反映其实时的状态，影响着弹跳机器人动作执行的有效性与完成度。因此，获取弹跳机器人的位姿信息以及信息的准确度，对于弹跳机器人有效执行动作具有突出的作用。然而MJR作为传感器节点，存在体积小、负载能力弱等问题，难以搭载具有高精度而体积大、重量大的传感器系统，存在位姿检测难的问题，限制了其实际应用。在团队早期研制的间歇性运动的MJR基础上，本文采用IMU对MJR姿态进行检测，实现了自复位以及自主航向调节功能。通过UWB对MJR进行定位，并通过实验验证位姿检测与控制的稳定性和准确性，为MJR节点自部署奠定了基础。

1 基于IMU的机器人姿态检测

本文采用一个9轴IMU模块对MJR进行姿态检测，该模块包含了3轴加速度计、3轴角速度计及3轴磁力计。MJR读取IMU模块返回的数据后加以处理得到姿态信息，并结合机械结构执行动作。

1.1 自复位中姿态角检测

在本文的MJR设计中，利用机器人底部的调节电机带动调节杆腿旋转，以实现展开式自复位，展开式自复位原理如图1所示。

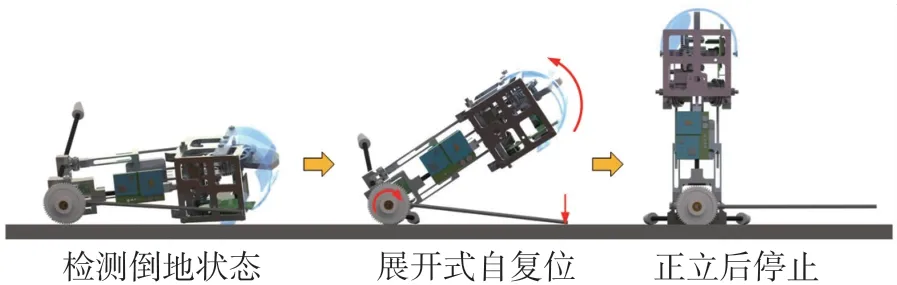
图1 MJR自复位示意图

MJR的自复位功能主要分为姿态检测与复位控制两部分。MJR会首先检测倾覆状态，通过检测到姿态角的正负判断机身的着地面，然后进行相应复位操作。自复位过程中，通过检测机身倾斜角度，并根据角度调节PWM输出，控制调节电机扭矩与转速。

当MJR处于静止时，三轴加速度传感器只受到竖直向下的重力，而当MJR倾斜时，重力加速度将在加速度传感器的三个轴向产生加速度分量，如图2所示。

图2 MJR姿态角示意图

机体坐标系下，将加速度计测量到的数据归一化为a＝[ax，ay，az]T。设绕X轴旋转的横滚角为ϕ，绕Y轴旋转的俯仰角为θ。IMU水平姿态绕Y轴旋转后可以得到关系:

再将IMU当前坐标系绕X轴旋转，可以得到IMU实际姿态下的输出为:

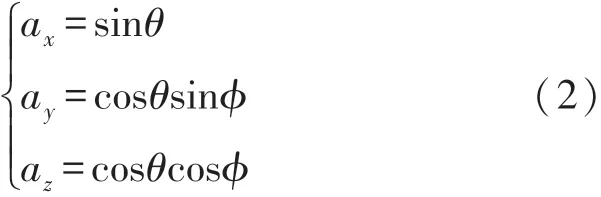
由此，通过式(2)可以得到姿态角为:

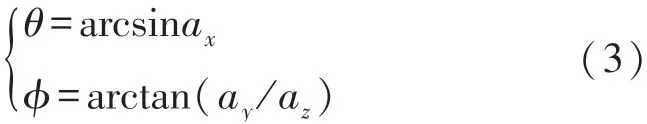
当检测到横滚角ϕ较大时，说明机身倾覆角度偏大，此时将PWM占空比设置较大，确保杆腿能获得足够的力实现复位。随着复位进行，检测到的ϕ逐渐变小，此时MJR所需复位力矩变小，减小PWM占空比。当检测到ϕ<β时，PWM占空比降为0，MJR会在惯性以及机身重力作用下完成复位。其中β为机身重心与地面支撑腿处于同一竖直线时的机身倾覆角度。随后采集一段时间姿态角信息，当检测到ϕ与θ均小于一定阈值时，则表明自复位成功。由于机身全高约12 cm，而重心高度约9 cm，且并不关于左右端面对称，实验中要实现MJR的稳定复位也存在一定困难。基于IMU姿态角检测实现自复位功能的工作流程如图3所示。

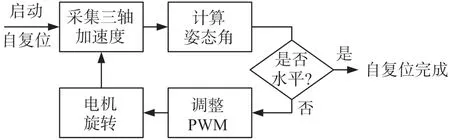
图3 基于姿态检测的自复位工作流程图

1.2 航向调节中航向角检测

在论文[4]中，杨茜等人对MJR姿态调节中离散和连续运动进行建模分析和实验研究，其中连续式航向调节机构由一个电机驱动，并利用单向轴承的特性进行机械解耦设计。

如图4所示，由调节电机带动轮子旋转以实现机身转动，而杆腿也会随之转动至另一侧。为了防止杆腿触地使得MJR侧翻，需要进行及时回调，在单向轴承作用下，杆腿回转而轮子保持不动，重复上述过程即可实现连续式航向调节。本文在团队研究基础上进行适当改进以及自主航向调节功能实现。在航向调节中发挥主要作用的传感器是磁力计，通过磁力计计算出MJR当前航向，结合目标航向角以及机身转动角度和电机转动角度的关系，可以转换为电机需要转动的角度。

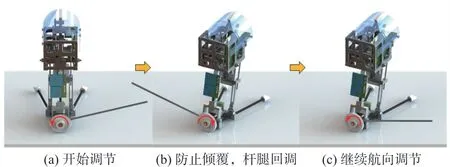
图4 连续式航向调节机构功能示意图

①磁力计基本原理

磁力计能够根据地磁场实时提供航向信息，通过测量地磁场矢量在各输出轴的分量以计算偏航角。偏航角基本公式如下:

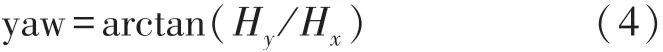
然而在磁力计非水平情况下，需要采用加速度计进行倾角补偿，将载体坐标系的XOY平面旋转到水平面，再计算航向角信息，解算过程如图5所示。

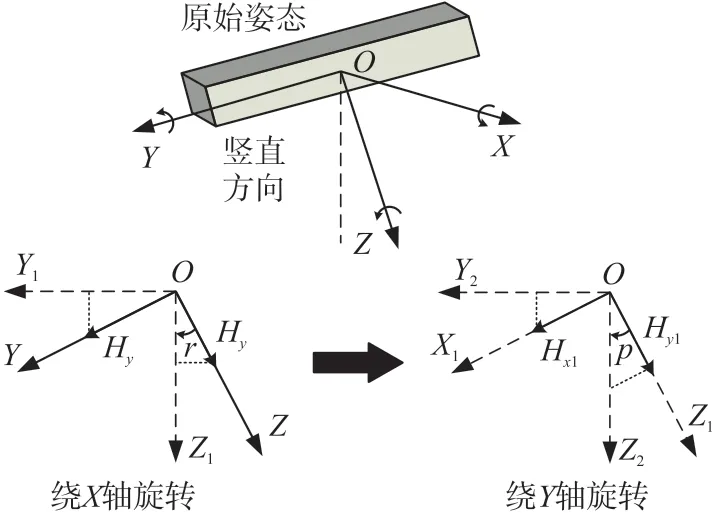
图5 非水平情况下航向角求解过程(倾角补偿)

第一步将磁力计所在坐标系绕X轴旋转r度，将Y轴旋转至水平面，如此可求得磁感应强度沿旋转后坐标系各轴的投影:

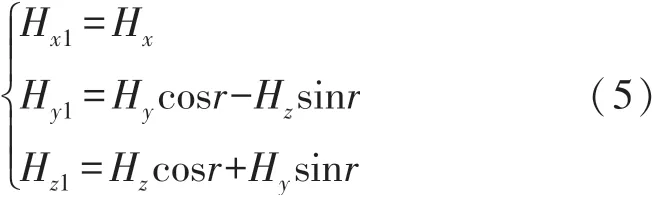
第二步将旋转后的坐标系绕Y轴旋转p度，如此已将原始磁力计坐标系中XOY平面旋转至水平面，旋转之后的各轴投影为:

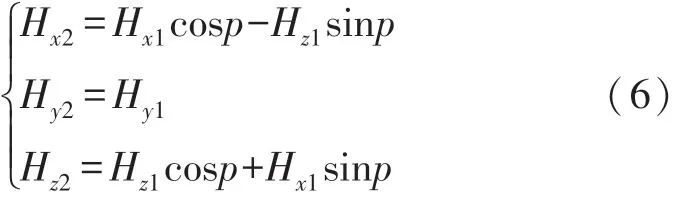
结合式(4)~式(6)，可得到一般情况下MJR航向角的表达式如(7)所示。

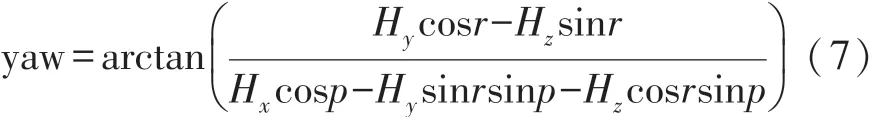
②磁力计校准

MJR机身上装备的各类元器件以及周围环境中的磁性材料等，都会对磁力计周围的磁场造成明显的影响，因而需要先对实验环境下的磁力计进行校准。

本文采用基于最小二乘的椭球拟合法对磁力计进行校准[16－18]，将MJR在实验环境中进行缓慢旋转，并采集磁力计数据。再将采集到的数据导入MATLAB中，利用椭球拟合法进行拟合，可以得到圆心坐标为(x0，y0，z0)，三轴长度分别为lx，ly，lz。如此可得校准后磁力计输出如式(8)所示:

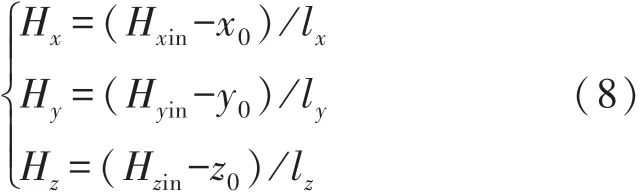
③磁力计辅助航向调节

本文采用带编码器的电机驱动航向调节，得到机身待转动角度后需要转换为电机转动角度。如图6所示，设MJR旋转半径为R，调节轮半径为r，机身转动角度为θ，那么电机转动角度φ为:

图6 航向调节平面示意图

此外，设电机轴转动一圈编码器得到的脉冲数为Cppr，调节电机减速箱的减速比为i，那么电机输出轴转动角度与对应脉冲数关系为:

因此结合式(8)与式(9)可以得到脉冲数与航向调整角的关系:

理论上通过编码器即可实现精准的航向调节，然而在航向调节过程中，由于地面粗糙度和坡度等影响，可能会导致旋转中心的改变，如图7所示。

图7 航向调节中旋转中心改变图

此外，调节轮打滑以及电机未及时刹停等因素都会导致航向调节不精确。因此，单纯依靠编码器控制航向调节并不可靠，本文结合了磁力计修正的方式来提升航向调节的可靠性。此种调节方式中，调节电机每旋转固定角度Dfixed(所需旋转角度>Dfixed时)就进行一次航向角检测，并更新剩余需要旋转的角度，不断调节直到偏差角小于设定的误差阈值，期间还要根据电机旋转角度及时将杆腿回调。其控制流程图如图8所示，其中Nfixed为Dfixed对应的脉冲数。

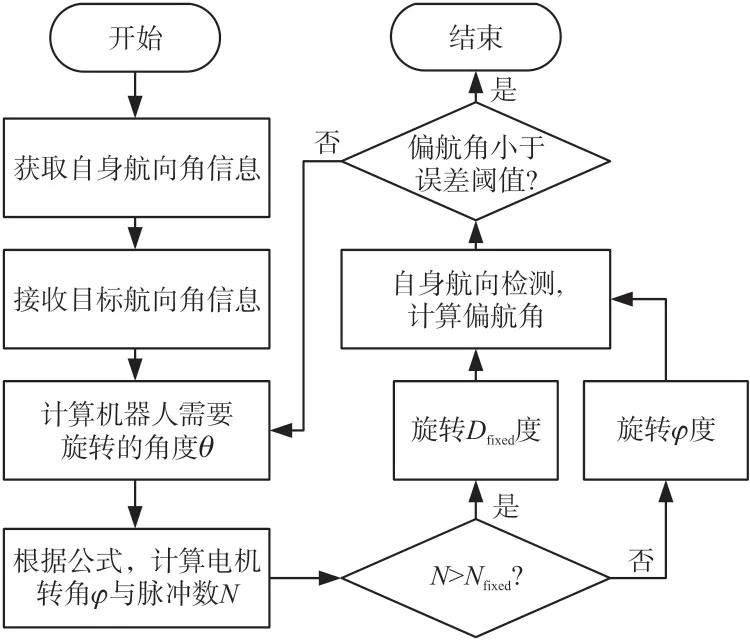
图8 结合磁力计修正的航向调节流程图

在航向调节过程中，由于机身重心较高，其可能会受到地面坡度等影响而跌倒。因此自主航向调节设计中，结合了姿态检测，确保MJR意外倾覆时，能够自主启动复位功能复位，并继续执行航向调节。

2 基于UWB的机器人定位方法

2.1 空间三边定位算法

在UWB定位技术[19－23]方面，目前常用的定位算法有直接计算法、Fang算法、Chan算法以及几何法等各类方法。本文采用几何法解算目标点，设置4个UWB基站，根据机器人与各个基站的距离信息以及基站的坐标，通过空间三边定位算法可以解算出MJR节点当前位置坐标信息，如图9所示。

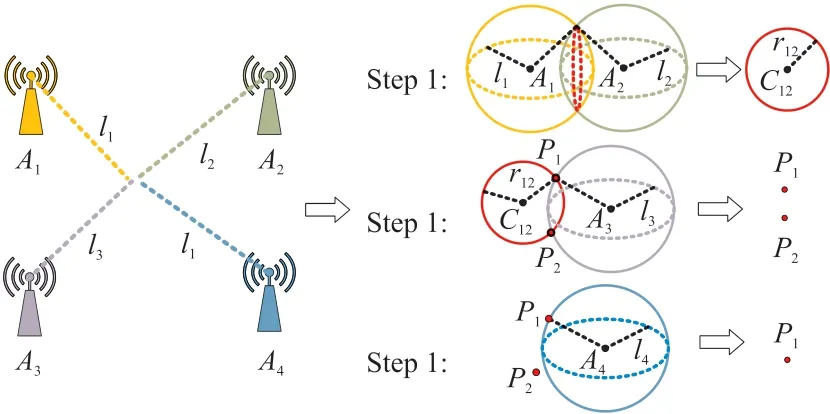
图9 UWB几何法解算示意图

设基站A1的坐标为(xA1，yA1，zA1)，基站A2的坐标为(xA2，yA2，zA2)，基站A3的坐标为(xA3，yA3，zA3)，以及基站A4的坐标为(xA4，yA4，zA4)，测距得到四个基站距离机器人的距离分别为l1，l2，l3，l4。设MJR当前坐标为(x，y，z)，则根据测得的与四个基站的距离信息，可以直接得到以下方程组(12):

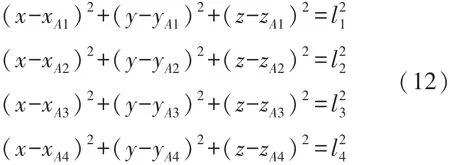
理论上，通过解这个方程组即可获得唯一解，作为MJR的位置坐标。然而实际上，由于UWB测距误差的原因，方程组很有可能是无解的，需要考虑对不同情况进行特殊处理以获得MJR位置的最优估计。

对于几何法实现球面定位解算的步骤基本如图9所示，主要分为三步:

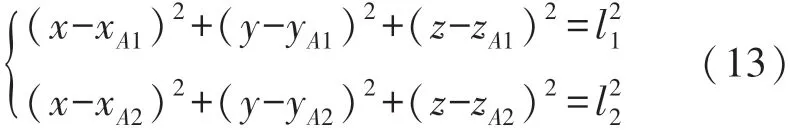
STEP 1 先选取其中A1与A2两个基站，由于测距误差的影响，两个球面可能有相交、相切与分离三种情况，即方程组(13)会对应存在无穷解、唯一解以及无解的情况:①对于一般相交的情况，交点的集合为一个圆。②而对于相切的情况，唯一解即为两个球面的切点。③对于两个球面分离的情况，我们需要逐步且适当地扩大两个球面的半径，即基站A1与A2返回的测距值，直到两球面相交或相切为止。

STEP 2 从STEP 1中我们解算得到的是一个空间中的圆，或者是一个点:①若为一个点，那么判断该点是否处于基站3的球面上，是那就返回该点作为结果，不是就返回失败。②若得出的是一个圆，那么求解圆与基站3的球面的相交情况:如果相切，返回切点坐标作为结果；如果相离，返回失败；如果相交，计算出两个交点用于下一步骤的计算。

STEP 3 从STEP 2中可以得出两个交点，设STEP 2中求出的两个交点坐标分别为P1(xP1，yP1，zP1)，P2(xP2，yP2，zP2)，联合直线方程与基站4球面方程(14):

将直线方程与基站4球面坐标方程联合求解，再根据交点分布情况以及P1P2离基站4球面的距离情况，进行分情况讨论处理:①假如过两个交点的直线与基站4的球面无交点，那么不断扩大球面4的半径；若是扩大到一定值仍无交点，则直接取P1P2两点中离球面4更近的那个点作为结果。②假如直线与球面4存在交点，如图10几大类情况，那么根据具体情况对P1和P2点进行加权处理求得最优估计位置坐标。

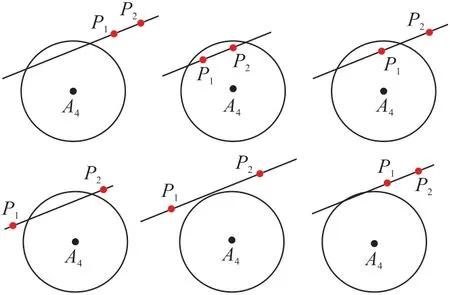
图10 交点相对关系示意图

2.2 UWB测距标定

由于周围环境中的金属以及障碍物等会对UWB信号产生吸收和阻挡等影响，使得UWB测距值出现较大偏差。因此，针对实验环境，需要事先进行UWB测距标定实验，对输出测距信息进行线性拟合以获取更加精确的测距结果。

在测距标定实验中，将MJR置于地面，UWB基站则放置在三角架上。其中MJR装备的信标UWB模块离地距离12.5 cm，基站UWB模块离地120 cm，即两者的垂直高度差为107.5 cm。在标定实验中水平距离间隔50 cm进行一次采集，从水平距离200 cm到800 cm一共采集13组。由于UWB在MJR上的安装位置不具备对称性，因此每组实验对MJR前后左右四个朝向分别进行检测记录，得到测距值如表1所示。

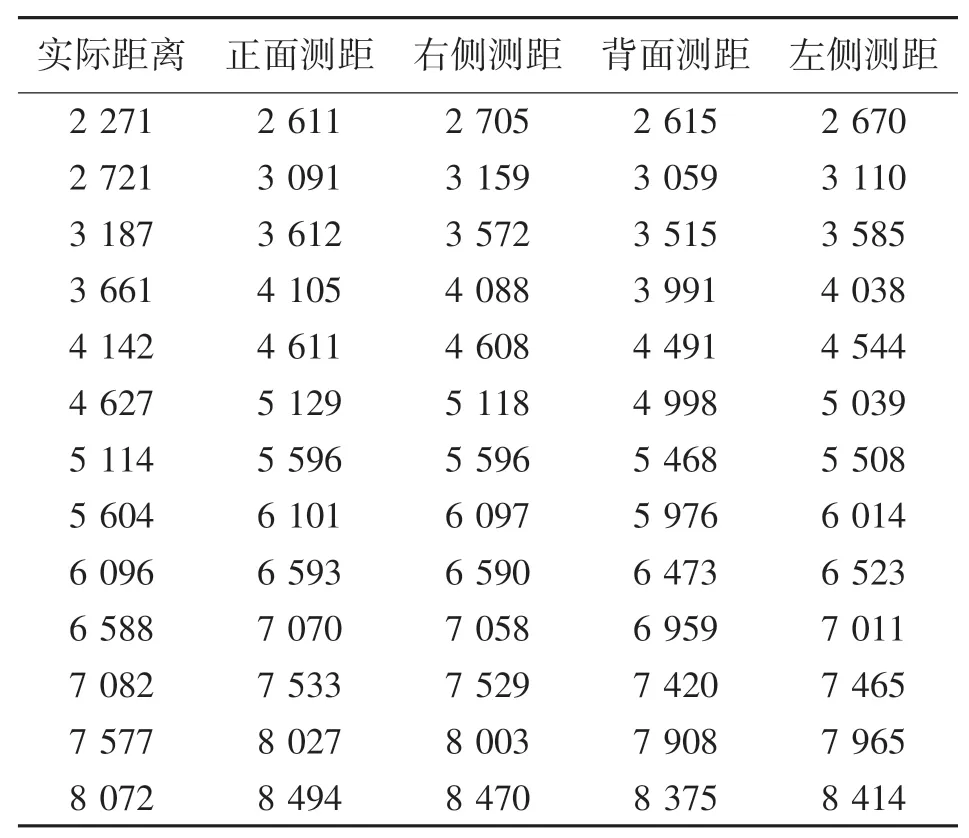
表1 UWB测距标定实验数据(4方向)单位:mm

将实验测距数据整理绘图，得到如图11结果，可以明显地看出，输出距离值基本呈现线性递增关系。本文采用四个方向测距均值替代MJR的测距信息，并在MATLAB中对测距均值采用二次项拟合，得到拟合式(15):

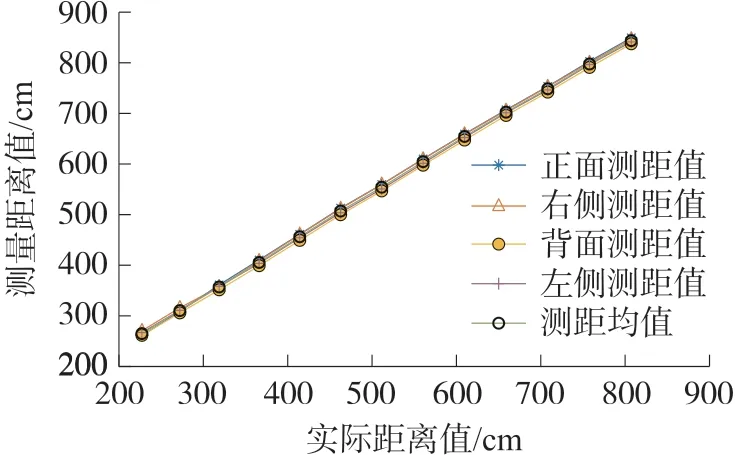
图11 UWB原始测距值变化曲线

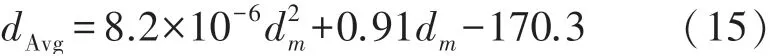
式中:dm为UWB返回原始测距值，dAvg为拟合后输出测距值。

采用拟合函数对原始数据进行处理，并计算与实际距离值的偏差，得到效果如图12所示。从图12中可以明显看出，经过二次项拟合之后的UWB测距信息更加符合实际测距值，并且测距偏差显著降低，基本稳定在±5 cm之间，这为之后MJR的UWB定位效果提供了一定的基础条件。

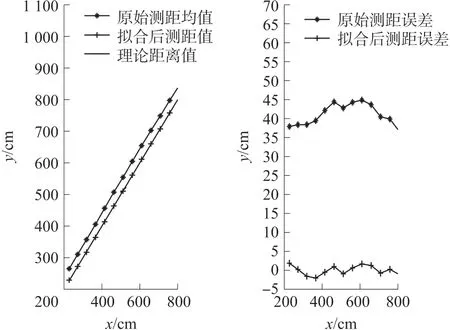
图12 二次项拟合效果图

3 实验测试

本部分首先对MJR的自复位姿态检测和自主航向检测效果进行了实验测试，在此基础上，通过MJR运动部署实验，验证本文提出方法的有效性。

3.1 节点自复位姿态检测实验

对MJR节点自主复位功能进行实验测试，测试其基于IMU姿态检测的自主复位功能的成功率。MJR节点可能一次复位成功，也可能首次复位不稳导致倾覆而从另一侧进行复位，本文实验中将超过连续4次以上复位运动以及其他未能复位的情况视为失败。自主复位实验一共分为两组，一组初始状态为左侧倾覆，另一组初始状态为右侧倾覆，对每组实验分别进行40次重复测试，记录复位结果如表2所示。

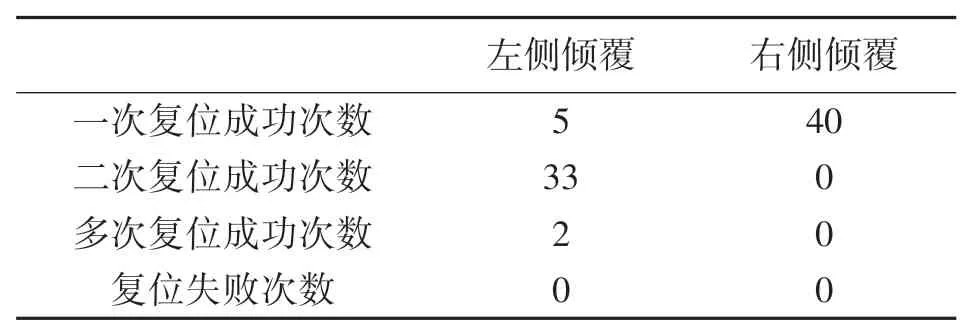
表2 两种倾覆状态下自复位实验结果

从表2中可以看出，针对两种初始倾覆状态下的自主复位实验均未出现复位失败的情形，这说明了基于IMU的自主复位功能的稳健性。

可以看出当MJR基本都是从右侧成功复位，出现该现象的原因是MJR样机的重心偏向于机身右侧，如图13所示。

图13 两种倾覆状态下重心位置示意图

相同机身倾斜角度α下，左侧倾斜下重心－旋转轴－杆腿的夹角更大。而当机身姿态接近水平时，是依靠惯性以及自身重力实现复位的，即从此时到机身水平，左侧倾斜复位情况下重心位置绕旋转轴转过的角度更加大，也就更加容易出现再次倾覆的现象。

在自复位实验过程中采集机身倾角信息，取其中典型的几组实验数据在MATLAB中绘制如图14所示。从图中可以看出，一次复位成功情况下，机身倾角绝对值从90°附近不断减小至15°左右，随后MJR可在惯性与重力作用下完成复位。而在二次复位或多次复位情况下，MJR均出现了复位立正后再次倾覆的情况，不过MJR检测到再次倾覆后会继续从另一侧进行复位，直到成功调整机身至水平稳定。

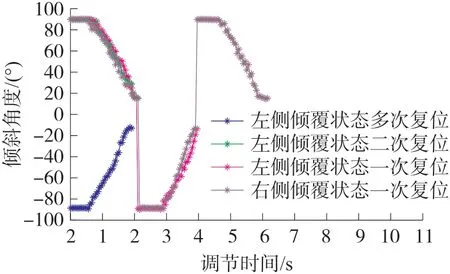
图14 自主复位过程中机身倾角变化示意图

3.2 节点自主航向调节实验测试

针对单纯依靠编码器进行航向调节以及磁力计修正的航向调节方法进行对比实验，实验中控制MJR进行固定航向调节(45°~360°，每隔45°设置一组实验)。由于磁力计航向检测以及航向调节均存在一定误差，为了确保自主航向调节功能的效率，实验中MJR节点检测到航向调节偏差处于5°以内即视作调节成功，并自动停止该次航向调节运动。对每一组航向角调节实验进行5次，取均值作为结果，并计算每组调节实验的角度偏差以及方差，结果如图15、图16及表3所示。

表3 两种航向调节方式的调节角度方差(单纯编码器，编码器＋磁力计修正)

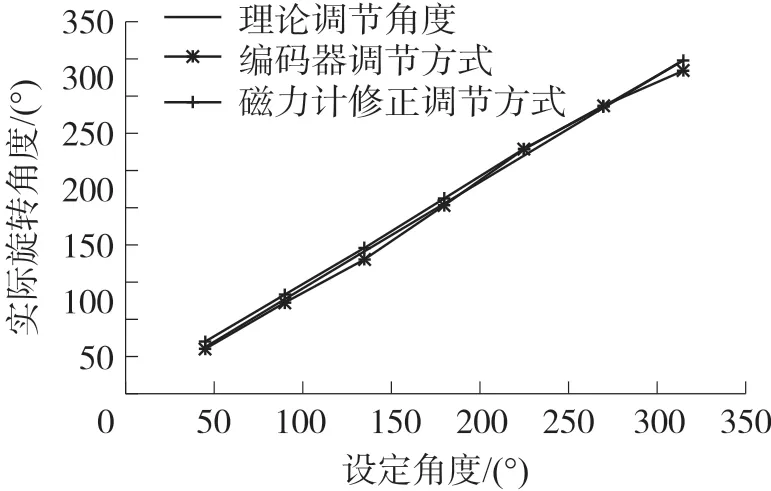
图15 两种航向调节方式对比图

图16 调节角度偏差与方差对比

通过自主航向调节实验得到的单纯编码器航向调节方式的平均调节角度偏差为4.64°，调节平均方差为13.25。编码器结合磁力计修正的航向调节方式平均调节角度偏差为3.64°，调节平均方差为0.65。可以明显看出，采用磁力计修正航向调节的方式相比单纯采用编码器，有效地降低了旋转中心改变以及调节轮打滑等对航向调节的影响，具备更高的准确性和稳定性。

3.3 节点运动部署定位实验测试

本文基于上文MJR基础功能的实现以及提出的定位方法，设计了直线和矩形轨迹跳跃的部署运动验证MJR基础功能的稳定性与定位功能的准确性。

直线跳跃部署运动实验设置为8跳，共进行2次实验。矩形跳跃部署运动实验设置为16跳，约为2 m×2 m的正方形，共进行1次实验。如图17所示，实验场地设置为5 m×8 m，在场地的四个边角处分别放置一个UWB定位基站，用对MJR运动过程中每次的落地位置进行定位。

图17 户外实验场景图

在直线跳跃部署运动中，将MJR置于起始点(250，200)，通过上位机向MJR发送跳跃方向以及单跳指令。MJR接收指令后，将自主进行航向调节，调整至设定方向后进行跳跃，落地后进行自动复位，MJR姿态调整完毕之后利用UWB基站进行定位，并将定位结果发送至上位机，每组实验共执行8次连续单跳运动。矩形跳跃中，MJR初始位置位于点(150，300)处，发送指令控制MJR自主按照顺时针方向跳跃，每个方向进行4次跳跃，使得运行轨迹基本符合矩形。

测量每次弹跳落地后的实际位置以及UWB返回的位置信息，在MATLAB中绘制折线图表征实验运动轨迹，如图18、图19所示。

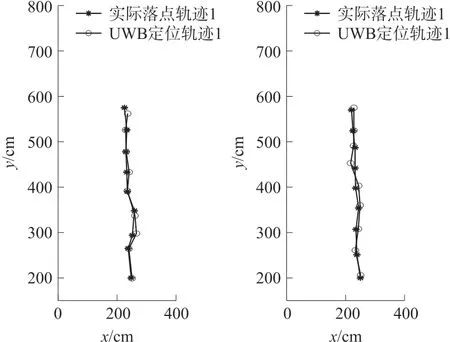
图18 直线跳跃运动及定位效果

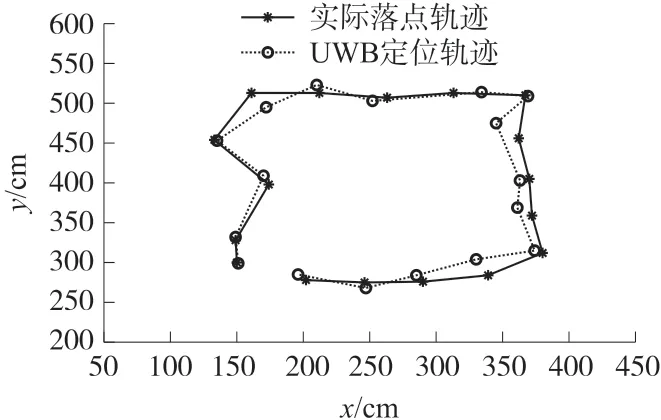
图19 矩形跳跃运动及定位效果

通过直线以及矩形运动轨迹可以看出，基于姿态检测的MJR自复位以及航向调节功能具备一定的稳定性。MJR在运动过程中，可能出现某几跳落点不够均匀，其产生的原因主要是是MJR落地时二次起弹，此外MJR落地后自复位会导致一定的位置偏移。

通过分析跳跃运动中实际落点与UWB定位落点位置的差距，得到UWB定位的平均偏差为9.08 cm，定位误差基本能保持在23 cm以内，这反映了MJR采用UWB定位方式具备一定的稳定性与精确性。

4 结论

本文基于实验室早期研制的仿生MJR，利用IMU对机器人的姿态进行检测，实现了自主复位功能以及自主航向调节功能，并通过实验验证了稳定性与精确性。此外，本文对基于UWB定位方式进行研究，并通过实验验证了该定位方式的可行性与精确性。基于上述基础功能设计以及UWB定位的实现，进行了直线和矩形轨迹的部署运动实验测试，对每次落点进行定位测试，得到平均定位精度为9.08 cm。本文所提出的基于IMU和UWB的MJR位姿检测方法，可为负载受限的移动传感器节点位姿检测提供借鉴；所实现的MJR自部署功能可提高复杂环境中移动传感器网络的网络覆盖率，实现环境监测、灾害搜救中继等功能，具有很好的应用前景。