三稳态压电振动能量采集器的非对称势能阱产生机理及其动力学特性研究∗
2021-10-27洋郑友成朱强国李颍赵泽翔王光庆
鞠 洋郑友成朱强国李 颍赵泽翔王光庆
(浙江工商大学信息与电子工程学院(萨塞克斯人工智能学院),浙江 杭州310018)
近年来,低功耗电子设备如无线传感器、通信节点、微型机器人、无人机以及可穿戴(可植入式)等的飞速发展与广泛应用,使其供能技术受到严峻的挑战。传统电池供能虽然便捷,但是使用寿命短,无法长时间稳定地供能。一方面电池体积较大,难以满足低功耗电子元件微型化的发展需求;另一方面更换电池费时费力,被更换的电池处理不当容易造成环境污染。因此,如何替代电池实现对低功耗电子器件自供电是迫切需要解决的技术瓶颈。将环境中普遍存在的振动能量收集并转换成电能,实现对低功耗电子器件和无线传感器网络自供电成为研究热点。当前,基于压电转换原理的振动能量采集技术因其能量转换密度高、结构简单、无污染、且易与宿主结构集成等优点受到关注[1]。
早期研制的压电振动能量采集器主要是由压电双晶/单晶悬臂梁及其末端质量块构成的线性机电转换系统,它们仅在结构的固有频率附近有较大的功率输出。为了拓宽压电振动能量采集器的有效工作频带和提高其能量转换效率,采用非线性多稳态振荡技术使器件在多个势能阱之间作大幅值的高能轨道运动成为当前研究的重点。Tang[2]、Erturk[3-4]和Litak等[5-7]人利用磁体之间的非线性磁力,研究了双稳态压电振动能量采集器的动态输出特性。Wang[8]和Zhou等[9-10]从理论和实验方面研究了非线性三稳态压电振动能量采集器,结果表明三稳态能量采集器较双稳态采集器具有更宽的工作频带和更高的能量转换输出。Kim和Seok[11]利用悬臂梁末端磁铁与外部两个磁铁之间的排斥力研制了一种三稳态压电能量采集器,通过降阶模型对比分析了三稳态压电能量采集器能在激励幅值较小时实现高效率的机电转换。孙仲生[12]等研究了非线性系统在低频宽带振动下悬臂梁的共振机理,通过数值和实验验证了非线性双稳态系统具有更高的输出电压。赵泽翔等[13-15]根据Hamilton原理和Raleigh-Ritz方法建立非线性三稳态机电耦合动力学模型并实验,得出磁铁间距、激励幅值以及频率等参数对系统动力学特性和电压输出特性的影响。上述研究证明了非线性技术可以使压电振动能量采集器的工作频带和转换效率提高。然而上述研究的非线性压电振动能量采集器具有一个共同的特征就是它们的势能阱具有对称性、且势能阱的深度和宽度是固定不变的。这使得非线性振动能量采集器在低激励水平下很难突破势能阱的束缚实现大幅值的高能轨道运动,导致其性能大大降低。最近,有研究开始关注带有非对称势能阱的压电振动能量采集器,韩研研[16]等研究了几何非线性在双稳态系统中的大幅周期和混沌运动下的输出性能。李海涛等[17]针对带有非对称势能阱的双稳态能量采集系统开展混沌动力学研究。然而,非对称势能阱的产生机理及其对能量采集器动力学特性的影响机制还尚未清楚。本文针对三稳态非线性压电振动能量采集器,考虑几何非线性和重力效应,建立其非线性机电耦合动力学模型,仿真和实验研究分析几何非线性和重力效应对系统动力学特性的影响规律及非对称势能阱的产生机理。研究成果为研制高性能多稳态压电能量采集器提供理论和实验参考依据。
1 多稳态压电能量采集器理论模型
如图1所示,三稳态非线性振动能量采集器由长度为L的悬臂梁以及附着在梁根部的一对长为Lp的压电片组成。压电片与负载电阻R直接串联;质量为Mt的磁铁固定于悬臂梁的末端(称为末端磁铁A)。两个外部磁铁(磁铁B、磁铁C)固定在基座上,其垂直间距为dg,与末端磁铁A之间的水平距离为d。z(t)为激励振动位移,¨z(t)=A0cos(ωt)为振动加速度,其中A0示振幅,ω为激振频率。
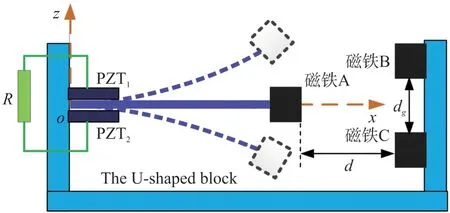
图1 非线性三稳态压电振动能量采集器
以悬臂梁根部中心为原点建立坐标轴,水平为x轴方向,垂直为z轴方向。考虑悬臂梁大变形产生的几何非线性建立采集器动力学模型。大扰度压电悬臂梁应变与位移之间的关系式可采用如下非线性表达式
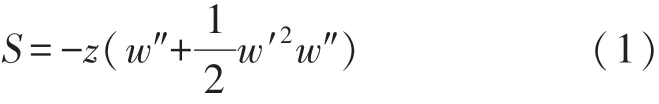
式中:z为悬臂梁任意一点到中性面的垂直距离,w为悬臂梁垂直方向振动位移。压电陶瓷的应力-应变关系采用线性压电本构方程,并且假设压电片上所受到的电场强度是均匀分布的。
系统动力学方程采用广义哈密尔顿原理来推导,即
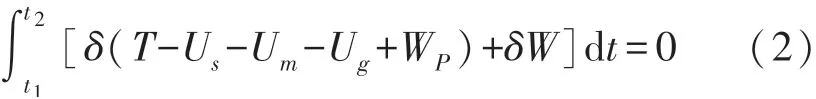
式中:T为系统的动能;Us,Um和Ug分别为压电悬臂梁的弹性势能,磁场势能和末端磁铁A的重力势能;WP为压电片的电势能,其中

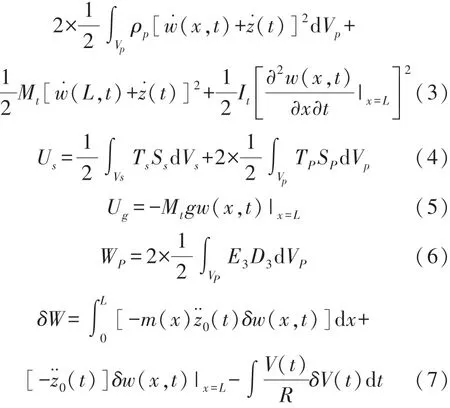
式中:ρs和ρp分别为采集器金属基体和压电片的密度;Vs和Vp分别为金属基体和压电片体积;Ts和Tp分别为金属基体和压电片的应力;Ss和Sp分别为金属基体和压电片的应变;Mt和It为末端磁铁的质量和转动惯量;g为重力加速度;V(t)为采集输出电压;R为负载电阻;m(x)为压电梁单位质量。
末端磁铁受到外部磁铁的排斥力可以利用点磁荷偶极子理论计算得来[16],末端磁铁与外部磁铁之间的几何关系如图2所示。

图2 磁铁几何位置关系
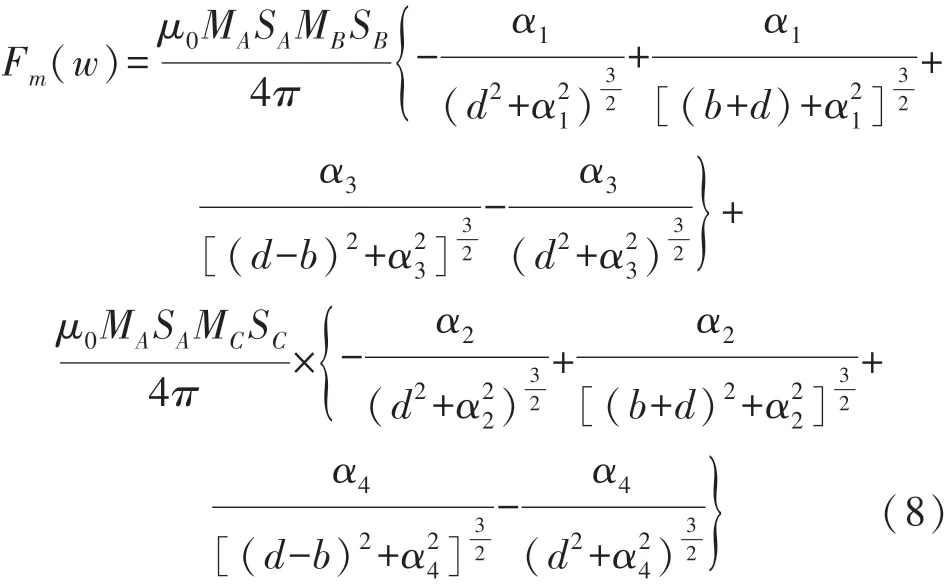
式中:α1=w(L,t)-0.5dg,α2=w(L,t)+0.5dg,α3=w(L,t)+bθ-0.5dg,α4=w(L,t)+bθ+0.5dg其中μ0=4π×10-7H/m是真空磁导率;MA、MB和MC分别是永磁铁A、B和C的磁化强度,同理,SA、SB和SC分别为永磁铁A、B和C的表面积;θ=∂w(L,t)/∂x是尖端磁铁的旋转角度。
因此,磁体间产生的势能可以通过积分表示出来
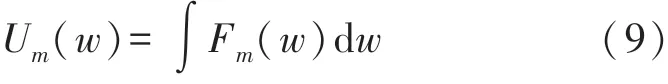
式(3)~式(9)中:w(x,t)可采用Galekin方法分离变量得到,即
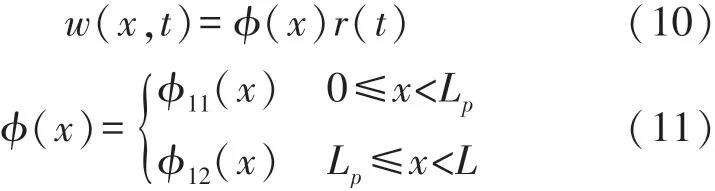
式中:ϕ(x)为压电悬臂梁一阶弯曲振型;r(t)为模态坐标;ϕ11(x)和ϕ12(x)分比为含压电片和不含压电片悬臂梁一阶弯曲振型。
将式(3)~式(11)代入式(2)中,根据拉格朗日方程可以得到考虑几何非线性和重力后的动力学方程:
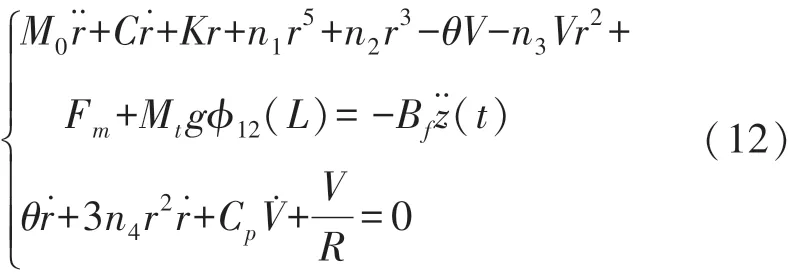
式中:
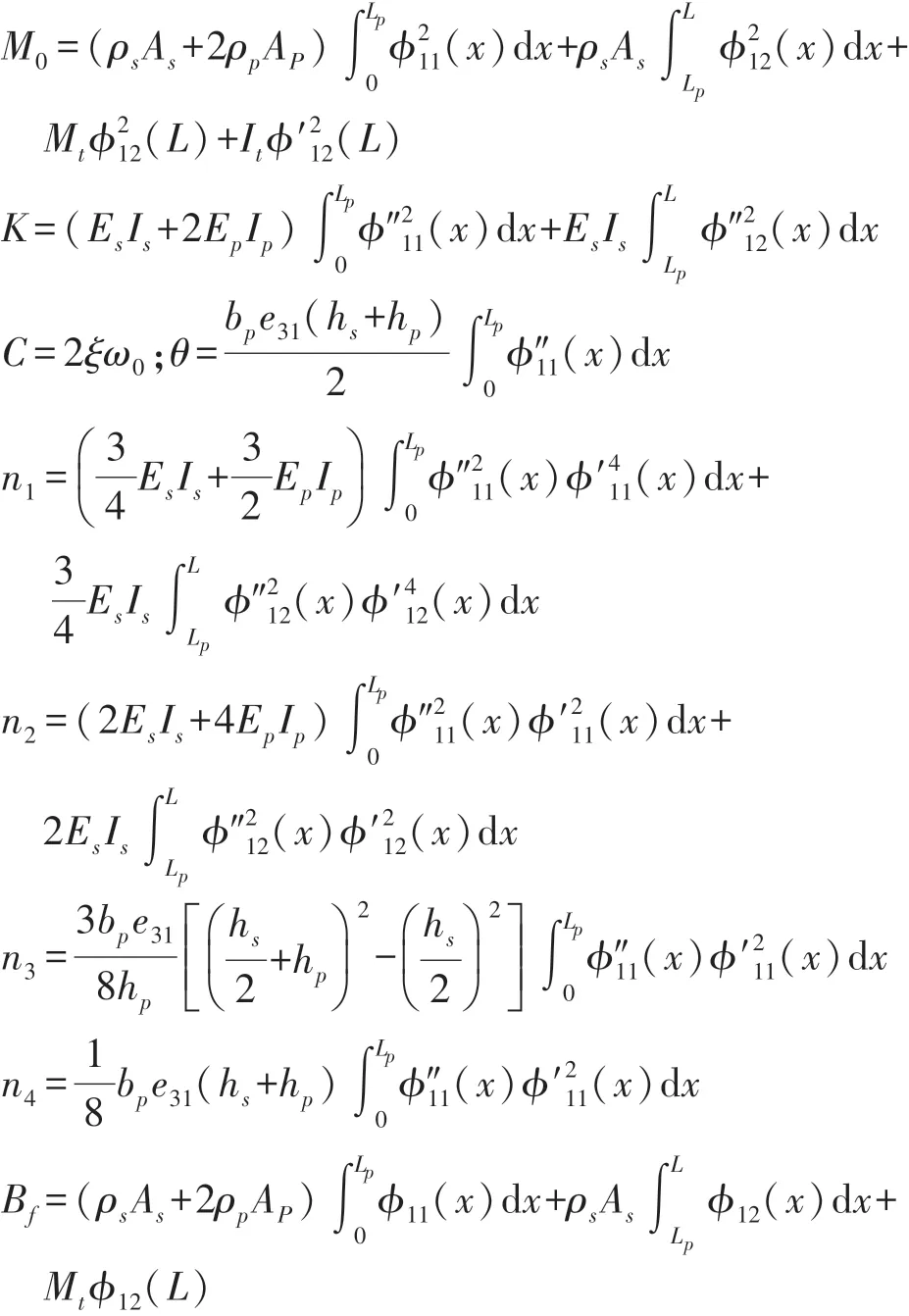
式中:EsIs和EpIp分别为基体和压电片的弯曲刚度;As和Ap为基板和压电片的截面面积;bp和hp为压电片的宽度和厚度;hs为基板厚度;e31为压电常数;ξ为机械阻尼系数;ω0为悬臂梁一阶弯曲谐振频率。
2 系统的动力学特性分析
2.1 几何非线性对系统响应特性的影响
由式(12)可以看出,压电悬臂梁几何非线性将引入附加的三次非线性刚度和五次非线性刚度。这里首先研究三次非线性刚度和五次非线性刚度对采集器输出特性的影响。
如图3所示是不同几何非线性刚度对采集器输出响应特性的影响结果。当不考虑压电悬臂梁的几何非线性时,即n1=0,n2=0,如图3(a)所示。此时压电能量采集器作高能轨道运动的频率范围为4.26 Hz~5.7 Hz。当n1=0,n2≠0时,如图3(b)所示,其宽频高能轨道运动范围变为4.30 Hz~8.72 Hz。当n1≠0,n2=0时,如图3(c)所示,其频带宽度变为4.26 Hz~5.96 Hz。当n1≠0,n2≠0时,如图3(d)所示,即完全考虑几何非线性时,系统的频带宽度变为4.28 Hz~10.73 Hz。由此可以看出考虑几何非线性后,能量采集器的频带宽度远大于不考虑几何非线性时的频带宽度。同时发现,三次非线性刚度n2比五次非线性刚度n1的频带更宽,这说明n2对三稳态采集器的动态响应特性影响较大。除此之外,考虑几何非线性时采集器的末端位移也优于不考虑几何非线性时的采集器。由此可以得到:考虑几何非线性不仅能够拓展频带宽度,还能增加末端磁铁的振动位移。
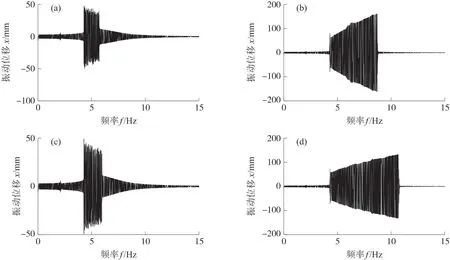
图3 几何非线性系数n1,n2对幅频响应的影响
2.2 末端磁铁重力对静态解分岔的影响
系统的静态解可以通过动力学方程式(12)得到,令¨r=̇r=̇V=V=¨w=0,得到:
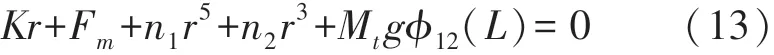
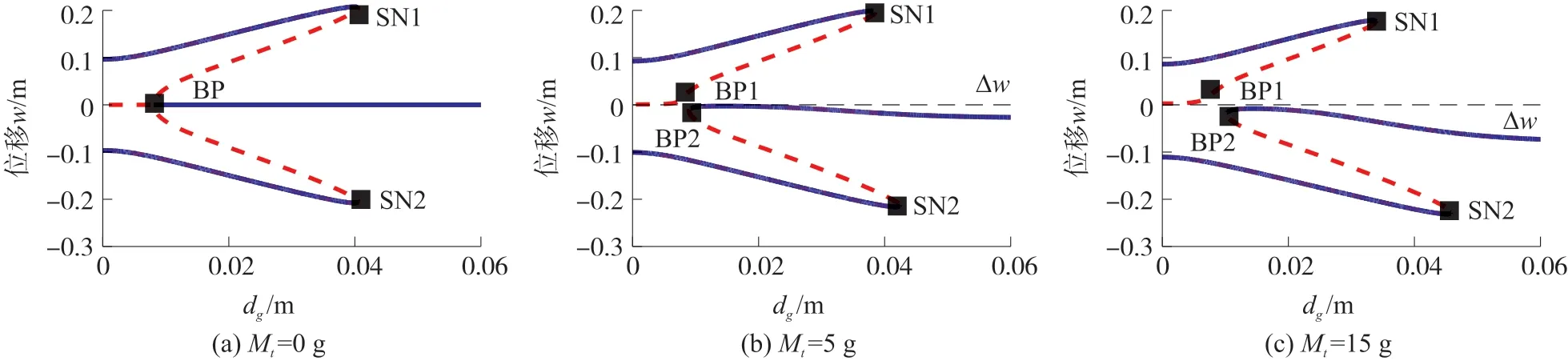
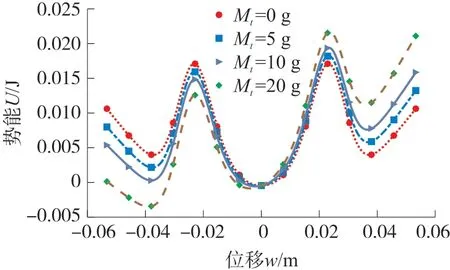
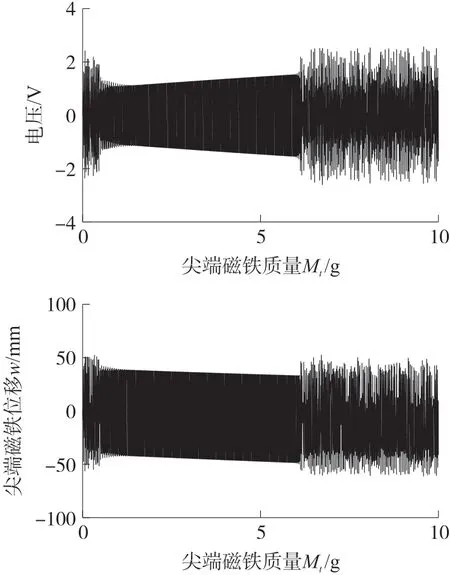
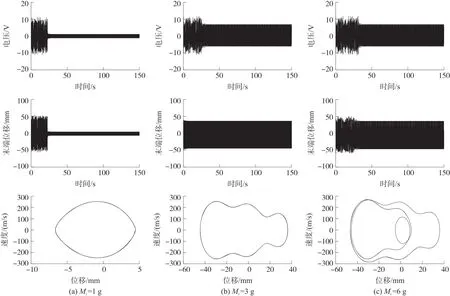
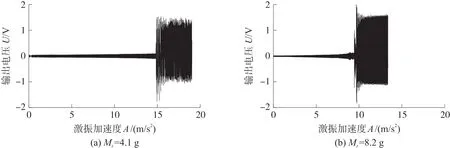
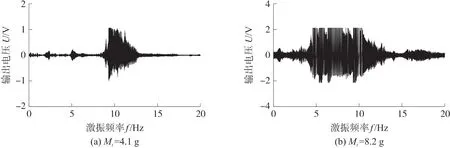
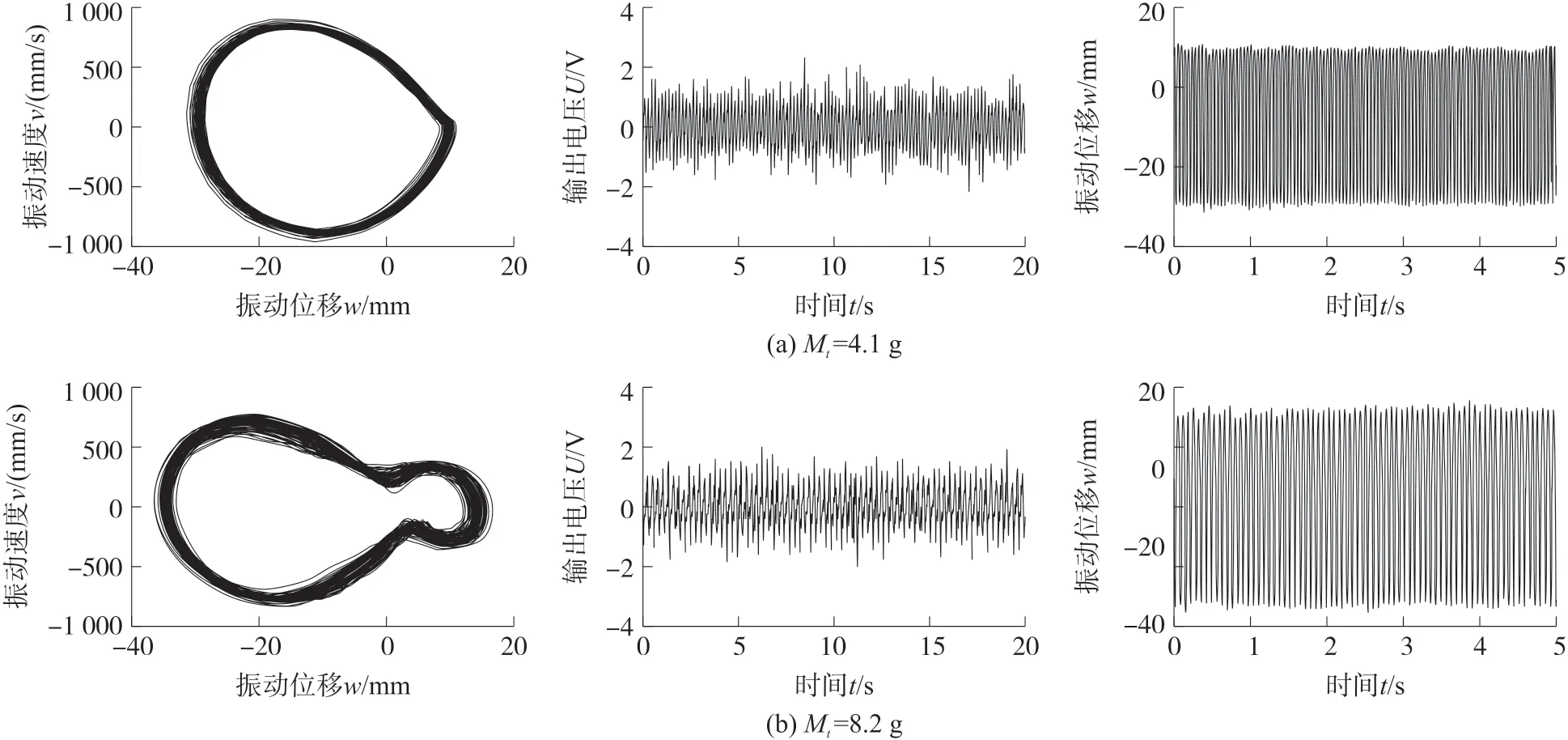
由式(13)可以看出几何非线性和磁铁重力使得系统产生了附加的非线性几何形变势能和重力势能。根据式(13)绘制了三稳态系统考虑几何非线性和重力的静态解分岔图,其中稳定解用实线表示,非稳定解用虚线表示。图4所示是dg=20 mm,Mt分别为0 g、4.1 g、7.0 g、10 g、13 g和20 g时的系统静态解分岔图。当Mt=0时,如图4(a)所示,相当于不考虑重力因素,在平衡解点BP1处观察到一个叉形分岔以及在平衡解点SN处观察到两个鞍形结点分岔。当d>dSN时系统只有一个稳定零平衡解,由于尖端磁铁和外部磁铁间距离过大,即采集器为单稳态运动。当dBP1 图4 采集器静态解分岔特性 根据上述分析,在给定dg的情况下,随着水平距离d的不断增加,系统会在三种运动状态之间转换;随着尖端磁铁重量Mt的增加,系统从对称的平凡稳定解变成不对称的平凡稳定解,且随着Mt的增加,偏移量Δw越来越大,最后会和下鞍形分岔点相交使三稳态运动状态更容易实现。 同样,我们也得到以dg为变参数的分岔图(dg,w),当d=20 mm时,在Mt=0时,如图5(a)所示,形成两个鞍形结点分岔SN和BP,存在两个非平凡稳定的平衡解以及两个非平凡不稳定的平衡解和一个平凡稳定的平衡解,且两个非平凡的稳定解和不稳定解都是相互对称的;当dg>dgSN时,系统做单稳态运动;当dgBP 图5 当Mt=(a)0 g、(b)5 g、(c)15 g时,考虑不同垂直距离dg的三稳态分岔行为 综上,可以得出尖端磁铁质量Mt可以改变系统静态平衡点的位置,使其呈现不对称性,并且增加Mt的质量,不对称现象越来越明显。除此之外,对比(d,w)和(dg,w)平面内的静态解分岔图可以看出,由于尖端磁铁的引力效应,上鞍型分岔点左移以及下鞍型分岔点右移造成能量采集系统出现三稳态运动的范围变小,这将导致采集器的动力学特性发生显著改变。因此,必须考虑末端磁铁的重力效应研究采集器系统的动态特性。 为了进一步研究Mt对三稳态运动状态的变化机理,根据式(4)、式(5)、式(9)可以得到系统的总势能U,利用MATLAB对系统势能进行仿真。如图6所示,Mt分别取0 g、5 g、10 g和20 g,可以看出采集器存在3个势阱和2个势垒;当Mt=0 g时(圆点),两侧的两个势阱中心坐标分别为(37.8 mm,4 mJ)和(-37.8 mm,4 mJ),可见两个势能阱是中心势能阱对称分布的;此时的最大势垒均为17 mJ,与图4(a)存在两个对称的静态平衡点相吻合。当Mt增加至5 g时(方块),势阱不再对称,而是形成了一个最高势阱(-37.8 mm,6.1 mJ)和一个最低势阱(-37.8 mm,2.3 mJ);此时,最高势垒与最高势阱之间的势能差为12.1 mJ,最低势垒与最低势阱之间的势能差为13.6 mJ。随着Mt的增加,最高势阱和最高势垒向上移动,最低势阱和最低势垒向下移动;当Mt增加到20 g时(菱形),最高势垒达到21.7 mJ,最低势垒达到12.3 mJ。这说明随着尖端磁铁质量的增加,三稳态能量采集系统可以很容易地克服势垒在三稳态系统中做阱间运动,从而表现出更好的能量采集特性。 图6 采集器不同末端质量时的势能 利用ODE45算法求解式(12),可以得到能量采集器在不同激励和初始条件下的非线性动力学特性,当dg=17 mm,d=26 mm,f0=5 Hz的情况下,我们得到了输出电压和能量采集器末端位移随Mt不断增加的关系图,如图7所示,可以看出输出电压在有效区间内随着Mt的增加而不断增加,且上下对称分布。由于考虑到末端磁铁受到重力因素的作用,尖端磁铁的振动位移由原来的关于原点对称振动到振动中心逐渐向下移动,最大正位移逐渐减小,最大负位移逐渐增大,这与静态分岔图得出的结论相符,考虑尖端磁铁的重力因素,三稳态能量采集器的运动是不对称的。 图7 输出电压、末端位移随尖端磁铁质量的变化情况 为进一步证明Mt对输出特性的影响,图8所示为Mt取值分别为1 g、3 g和6 g时采集器的采集电压、末端振动位移和相图。如图8(a)所示,当Mt=1 g时,采集器稳态时作小幅值的单稳态阱内运动,其输出电压和末端振动位移均比较小,输出电压幅值只有1.13 V,末端振动位移幅值只有4.45 mm;当Mt=3 g时,如图8(b)所示,采集器稳态时在三个势能阱之间作大幅值的阱间运动,表现出三稳态运动特性,输出电压和末端振动位移分别增大到6.2 V和36.4 mm;从相图可以发现,随着末端磁铁质量的增大,采集器的相图表现处明显的不对称性,其相图的中心左移,这是由于磁体质量的增大,导致静态解偏移水平位置下移。继续增大Mt到6 g时,如图8(c)所示,采集器稳态时的输出电压增大到了6.91 V末端磁体运动位移幅值为36.2 mm。由此可以看出,当末端磁体质量比较小时,三稳态能量采集系统做小幅度阱间运动,此时采集器的不对称性并明显,随着Mt的增加振动位移幅值和输出电压增加。但是较大的质量可能会使采集器末端位移减少,甚至使采集器在振动过程出发生断裂而损坏。因此,必须合理设计末端磁铁质量。从相图结果看,当Mt=1 g时采集器绕中心平衡点作小幅单周期振动,且此时的振动中心不为0,向左偏移一点,这与分叉特性的不对称相符。当尖端磁铁的质量增加时,采集器末端在3个稳定点之间跳动形成了周期三运动,此时的悬臂梁末端的运动速度由250 mm/s增加到1 270 mm/s作三稳态大幅度阱间运动。 图8 Mt=1 g、3 g和6 g时采集器采集电压、末端位移和对应的相图 图9 所示是采集器在dg=17 mm,d=26 mm,R=1 MΩ和A=10 m/s2时不同质量下的频率响应特性。如图9(a)所示,当Mt=1 g时,采集器在4.8 Hz~6.1 Hz之间作大幅度阱间运动,最大振动位移为30 mm,最大输出电压为0.65 V,最大功率为0.011 mW。此时增加尖端磁铁的重量,即Mt=4.1 g时,如图9(b)所示采集器大幅值阱间运动的频率范围扩到到4.6 Hz~7.6 Hz,末端振动位移增大到37 mm,输出电压增大为0.74 V,最大功率为0.022 mW。由此可以判断出,增大尖端磁铁的质量,不仅可以拓宽频带的带宽,还可以增加输出电压和功率的大小,提高能量采集的能力。 调整激励加速度幅值至A=20 m/s2,尖端磁铁的质量为1 g,如图9(c)所示,采集器作大幅值阱间运动的频带宽度为4.3 Hz~13.5 Hz,最大振动位移到146 mm,此时采集器作大幅度的全局阱间振动,对应的采集电压增加到10.3 V,功率为2.41 mW。对比图9(a)与图9(c)结果可以看出,增加激励加速度可以使能量采集系统更快速的进入大幅震荡。继续增加尖端磁铁的重量到4 g,如图9(d)所示,采集器作大幅值的阱间振动频带范围加宽,达到2.9 Hz~13.5 Hz,最大的振动位移、输出电压和功率分别达到147 mm、10.40 V和2.42 mW。因此,增大激励振幅和尖端磁铁的质量不仅可以提高能量采集系统的输出性能,还可以拓宽频带的带宽,让系统可以在更宽的频带范围进行能量采集。 图9 采集器末端位移、输出电压、输出功率随频率的变化情况 为了验证本文数学模型和仿真结果的正确性,研制了三稳态能量采集器实验样机,如图10所示,压电悬臂一端固定在基座上,另一端粘结一个永磁铁。在悬臂梁上下表面粘着两个相同的压电片,它们与外部负载电阻串联连接。两个大小相同的外部磁铁粘结在与末端磁铁水平相距为d的基座上,其磁场方向与悬臂梁末端磁铁相斥。 图10 三稳态采集器原理样机 图11 所示为采集器实验测试系统,三稳态压电振动能量采集器安装在激振器的支撑杆顶部;信号发生器产生的谐波信号经过功率放大器放大后激发激振器产生谐波振动采集器受谐波振动的影响产生不同的响应。基础加速度通过安装在其基础上的加速度传感器测量获得;采集器末端振动位移则通过激光位移传感器测得,采集输出电压通过示波器获取。最后,将所获取的所有信号送入动态信号分析仪分析输出。直流电源为整个测试系统提供必要的电能。 图11 三稳态能量采集器实验测试系统 首先实验研究末端磁铁质量对采集器动力学特性的影响,取系统参数f=4.5 Hz,A=10 m/s2,dg=17 mm和d=26 mm。如图12(a)所示,Mt=4.1 g时,系统做小幅度的阱内运动,此时的运动状态为单稳态周期运动,输出电压为0.6 V,振动位移范围为(-6 mm,4.3 mm);增加尖端磁铁的质量到8.2 g时,如图12(b)所示,此时系统做大幅度阱间运动,末端磁铁的振动位移范围增加至(-31 mm,28 mm),此时表现为三稳态运动状态,其输出电压增加至2.8 V,表明增大尖端磁铁的质量能够提高三稳态能量采集系统的动态输出特性,这与理论仿真结果的结果是一致的。 图12 Mt=4.1 g和8.2 g对应的时域响应(f=4.5 Hz) 图13 所示是不同磁铁质量采集器输出电压随激励加速度幅值变化的实验结果。由图13(a)可以看出当Mt=4.1 g,随着激励加速度的逐渐增大,采集器在A=15 m/s2时发生跳变,从小幅值的阱内运动跳跃到大幅值的阱间运动;当磁铁质量增大至Mt=8.2 g时,如图13(b)所示,采集器在加速度A=9.8 m/s2时发生跳变,从小幅值的阱内振动跳转到大幅度的阱间运动,输出较大电压。由此可以得到:增加尖端磁铁的质量可以减小系统做大幅度运动所需要的激振加速度,同时提高了系统的输出电压。 图13 Mt=4.1 g和8.2 g对应的加速度-电压图 图14 为采集器在dg=17 mm,d=26 mm,A=10 m/s2时的扫频图,当Mt=4.1 g时,如图14(a)所示,当激励频率在f<9.14 Hz时,系统做小幅度振动,输出电压在0.15 V左右;当9.14 Hz 为了进一步验证不同激励频率下末端重力效应对采集器系统动力学特性的影响,取激励频率f=11 Hz和激励加速度A=10 m/s2,其他参数与图12一致。当磁铁质量为4.1 g时,根据图14(a)的扫频实验结果得知采集器大幅值阱间振动的频率范围为9.14 Hz~11.2 Hz,由此可知当f=11 Hz时,此时采集器的振动为阱间大幅值的单周期运动,如图15(a)所示,与图12(a)所示的阱内振动相比,采集器的输出电压由原来的0.6 V增加到1.5 V左右,末端振动位移范围变成(-29 mm,10 mm)。当增大磁铁质量到8.2 g时,如图15(b)所示,采集器的振动由图12(b)所示的大幅值阱间三稳态运动变为阱间双稳态运动,采集器的输出电压由原来的2.8 V减少到1.6 V,末端振动位移范围变成(-35 mm,14 mm)。比较图15(a)和(b)实验结果可以发现,在较高激励频率作用下,增大末端磁铁质量依然可以有效提高采集器的输出性能。 图14 Mt=4.1 g和8.2 g对应的正向扫频图 图15 Mt=4.1 g和8.2 g对应的时域响应(f=11 Hz) 考虑悬臂梁的几何非线性和尖端磁铁的引力效应,建立三稳态压电振动能量采集器的非线性机电耦合动力学模型,并通过龙格库塔(ODE45)算法将其求解,通过对能量采集系统的动力学特性的仿真与实验分析,得到以下结论: ①悬臂梁几何非线性引入了附加的三阶和五阶非线性刚度项,有利于提高采集器的输出特性和频带宽度。 ②几何非线性和磁体重力效应导致系统的平衡点位置由零平衡点向下偏移,静态解分岔曲线不对称性越来越明显,且鞍型分岔点的位移分别向左右移动,三稳态存在的范围逐渐变小。 ③末端磁铁重力效应引入附加的重力势能,使得采集器的势能阱出现明显的不对称性,最低势垒随着末端磁铁质量的增加而减小,最高势垒随着Mt的增加而增加;非对称势能阱有利于采集器在较低的环境激励加速度条件下作三稳态阱间振荡,提高其能量采集输出效率和工作频带。 ④增大末端磁铁质量可以有效提高能量采集器的输出性能,拓宽其有效工作频带;但过大的磁铁质量可能会使采集器失效甚至损坏。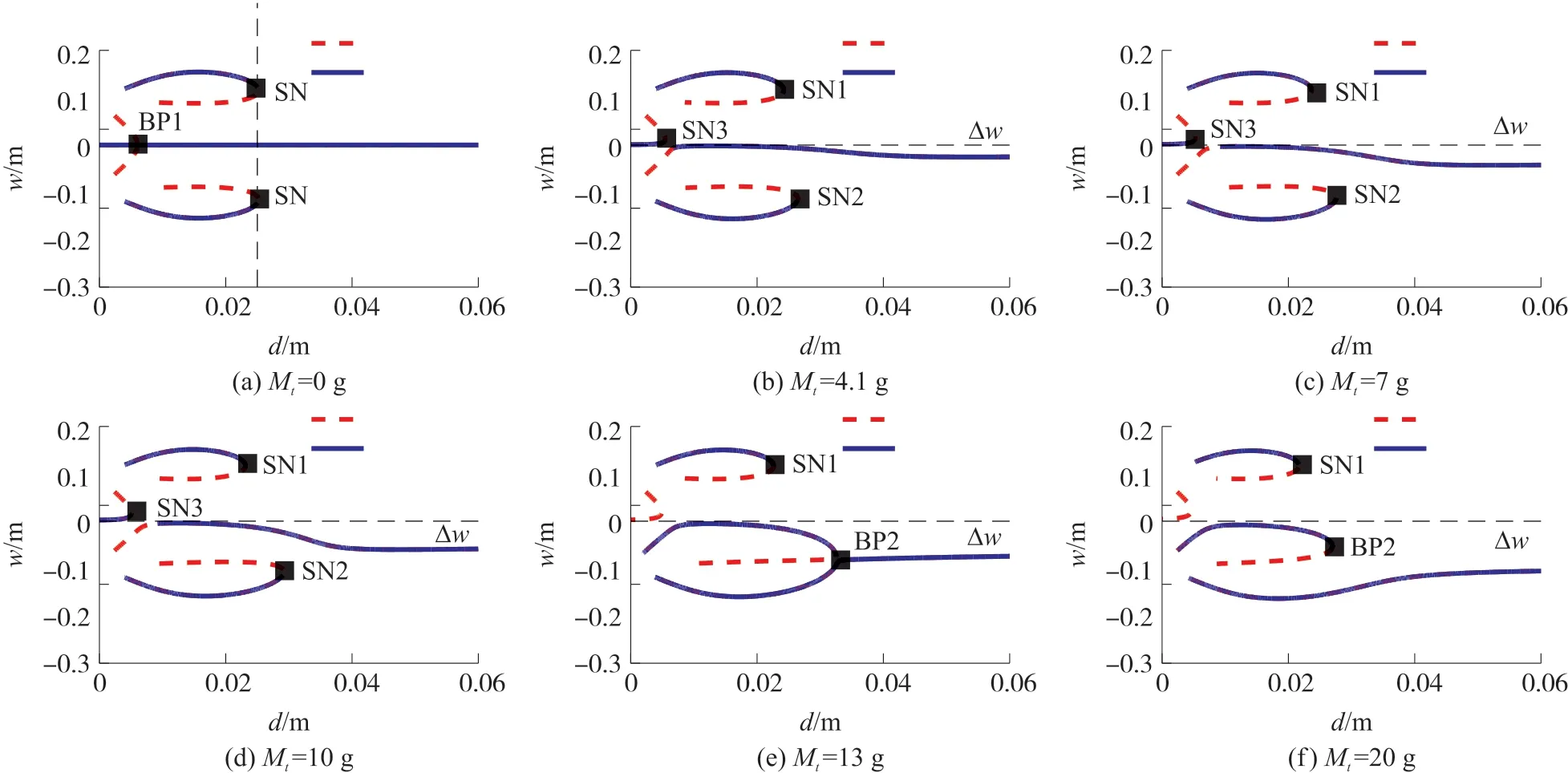
2.3 系统势能分析
2.4 末端质量Mt对动态输出特性的影响
2.5 能量采集器频率特性分析
3 实验研究与结果分析
4 结论
