涡旋压缩机轴向动态密封双提前量跟踪方法研究*
2021-10-27蔡炯炯张文辉倪凯华吴萱俊
蔡炯炯,张文辉,倪凯华,袁 熙,吴萱俊,瞿 晓
(1.浙江科技学院 自动化与电气工程学院,浙江 杭州 310012;2.墨尔本大学 工程与信息技术院,维多利亚州 墨尔本 3000)
0 引 言
作为一种以近直驱方式工作的容积式压缩机,涡旋压缩机具有压力稳定、效率高、振动小、噪声低、零部件少等优点[1-2]。但是由于其轴向气体分离力作用在动涡盘上,使动涡盘发生倾斜或脱离静涡盘,就会造成较大的气体泄漏和零部件的摩擦和磨损,这在一定程度上限制了涡旋压缩机的发展[3-5]。
在相同的转速下,大容量涡旋压缩机的排气量更大,但是这种涡旋压缩机存在体积大、能耗高、适用范围小的缺点。如果能改善涡旋压缩机的密封性,则可以使涡旋压缩机的转速更高、排气量更大、应用范围更广。因此,漏气问题是制约涡旋压缩机发展的一个难点。
目前,用以改善涡旋压缩机轴向力平衡的有针对性的方法有:(1)弹簧背压式[6]、推力轴承式[7,8]、气体背压式[9]、背压腔注入润滑油[10-12]和轴向随变机构[13];(2)在静涡旋盘的背面设置密封组件,以形成背压腔[14]。但是由于压缩机轴向气体分离力会随主轴转角的变化而呈现大幅度的变化,这些方案会因其动态响应慢,难以满足高精度、高动态性能的气体泄漏改善要求。
文献[15-17]采用电磁力来平衡涡旋压缩机的气体分离力,提出了以误差均方差为评价指标的自适应PID提前跟踪算法,改善了其跟踪滞后的缺陷[18-20],解决了该问题的主要部分。但使用该算法筛选出的最优提前角在线跟踪时,其上升段和下降段一般总处在一段略微过于提前,可以实现密封,而另外一段略微滞后,有泄露的缺陷;在高频时,由于其过压余量不足,又存在泄漏风险;同时,误差均方差指标无法判断过压密封状态或欠压密封性不足的状态,仍需要对其作进一步的改进和优化。
本文对误差方差和累积误差评价的平衡特点进行分析,提出以累积误差和均方差两种评价方法协同;提出在上升和下降段,分别采用不同的优化提前量,进行PID动态跟踪平衡的双提前量控制;给出基于提前量跟踪的自适应轴向动态密封算法;最后对该控制方法进行实验验证。
1 压缩机轴向电磁动态密封平衡
1.1 轴向气体分离力特征
在某一固定排气压力下,涡旋压缩机轴向气体分离力和主轴转角的关系[15]366如图1所示(此处取渐开线的圈数N=3,吸气口压力ps=0.8 MPa,渐开线节距P=12 mm)。

图1 轴向气体分离力
由图1可知:在吸气排气过程中,涡旋压缩机的轴向气体分离力是周期性变化的曲线,轴向气体分离力每隔360°转角一个周期,在单位周期内具有明显的上升坡道和下降坡道。
1.2 轴向电磁动态密封控制方案
采用带铁芯的电磁机构,以电磁力动态平衡轴向气体分离力的方案[15]366,具有大力密度、快速响应的优点。
涡旋机轴向力电磁平衡方案示意图如图2所示。
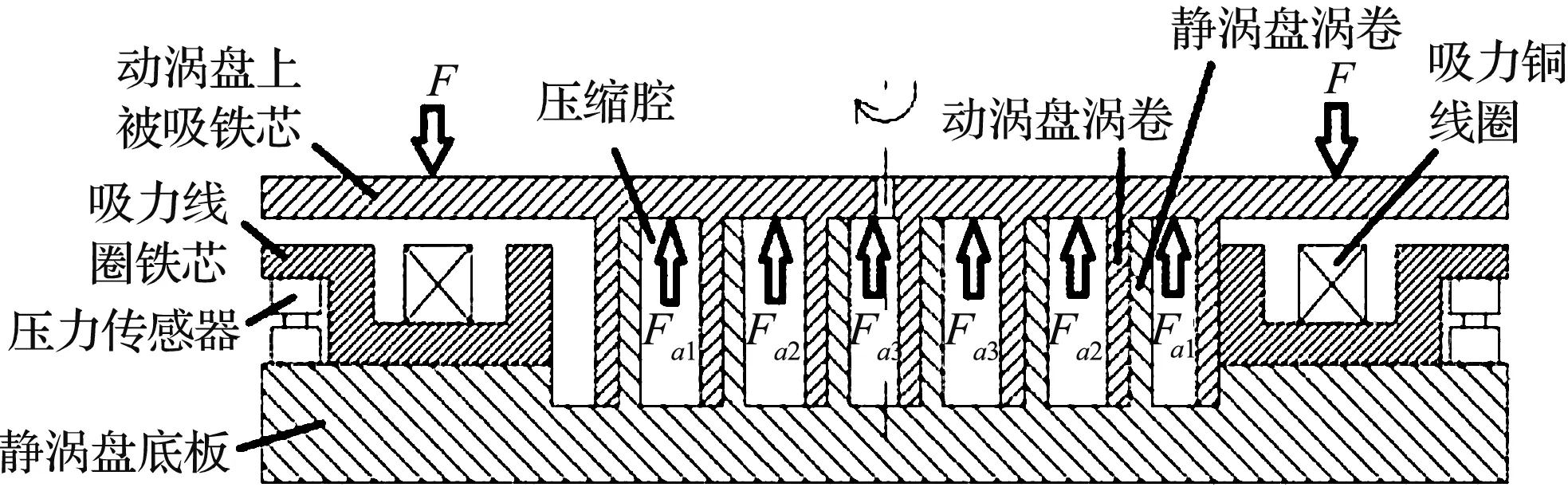
图2 电磁平衡方案结构
双提前量跟踪PID方法控制框图如图3所示。

图3 系统控制框图
图3中:在电磁铁电磁吸力动态控制中,PID控制环节为G1(s),驱动电路可以简化等效成惯性环节G2(s),控制对象的电流与电磁力之间的关系等效成带延迟特性的G3(s);将其与系统的控制目标R(s),反馈量C(s)组成一个闭环系统。
闭环传递函数可表示为:
(1)
式中:τ—系统提前跟踪时间最佳值。
在以离散方式执行时,嵌入式系统将体现出不同的提前步数[15]368。笔者提出在上升和下降段分别采用不同的优化提前量,以进一步优化压缩机的轴向动态密封效果。
1.3 理想平衡效果
一般的控制目标如图4所示。
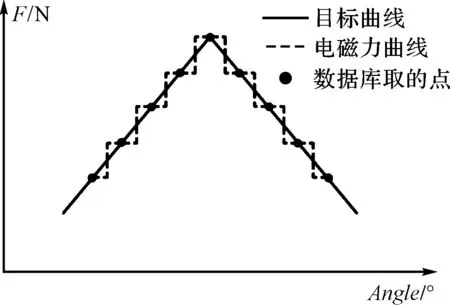
图4 一般的控制目标
笔者将涡旋压缩机工作时轴向力的每个周期按角度离散成n个点,建立“轴向气体分离力-位置角”数据库。数据库离散点如图4中圆点所示,实际跟踪点数为360,与文献[15]368中相同。为方便分析,此处简化跟踪对象,将离散点的点数取为9点;以PID算法跟踪目标轴向力产生电磁力曲线(由于以大小不同的离散点为跟踪对象,实际产生的电磁力曲线为类似阶梯状折线)。
为保证较好的轴向动态密封效果,电磁力与气体分离力需要达到平衡。一般的控制目标是,用图4中阶梯折线电磁力来平衡图中黑色气体分离力。然而这样的效果实际上无法达到,因为离散方式以实现时,嵌入式系统以目标点距为最小调整量,即总是超前或者落后一个点距;同时,电磁平衡力和目标线近似重叠的做法对确保密封也没有足够的余量。
实际目标的电磁力临界曲线如图5所示。

图5 实际控制目标
图5的实际实施过程中,是用折线1来达到大的动态效果,此时电磁力略过盈,牺牲少量磨损,但确保了系统具有最佳密封。
其中的具体过压量要根据实际进行调整(如图5中的折线2),但首要任务仍是找到临界曲线1。
2 单提前参数PID控制算法
2.1 控制算法寻优
文献[15]368是以误差方差作为跟踪效果的评价指标。在单提前参数PID 50 Hz的跟踪频率下,其最优提前步数对应的误差方差如表1所示。

表1 50 Hz频率寻优数据
表1中:在50 Hz下,19步为最优提前量,系统误差方差最小,为64.2。
2.2 控制算法实际效果
最优提前量平衡的实际效果如图6所示。

(a)略微滞后
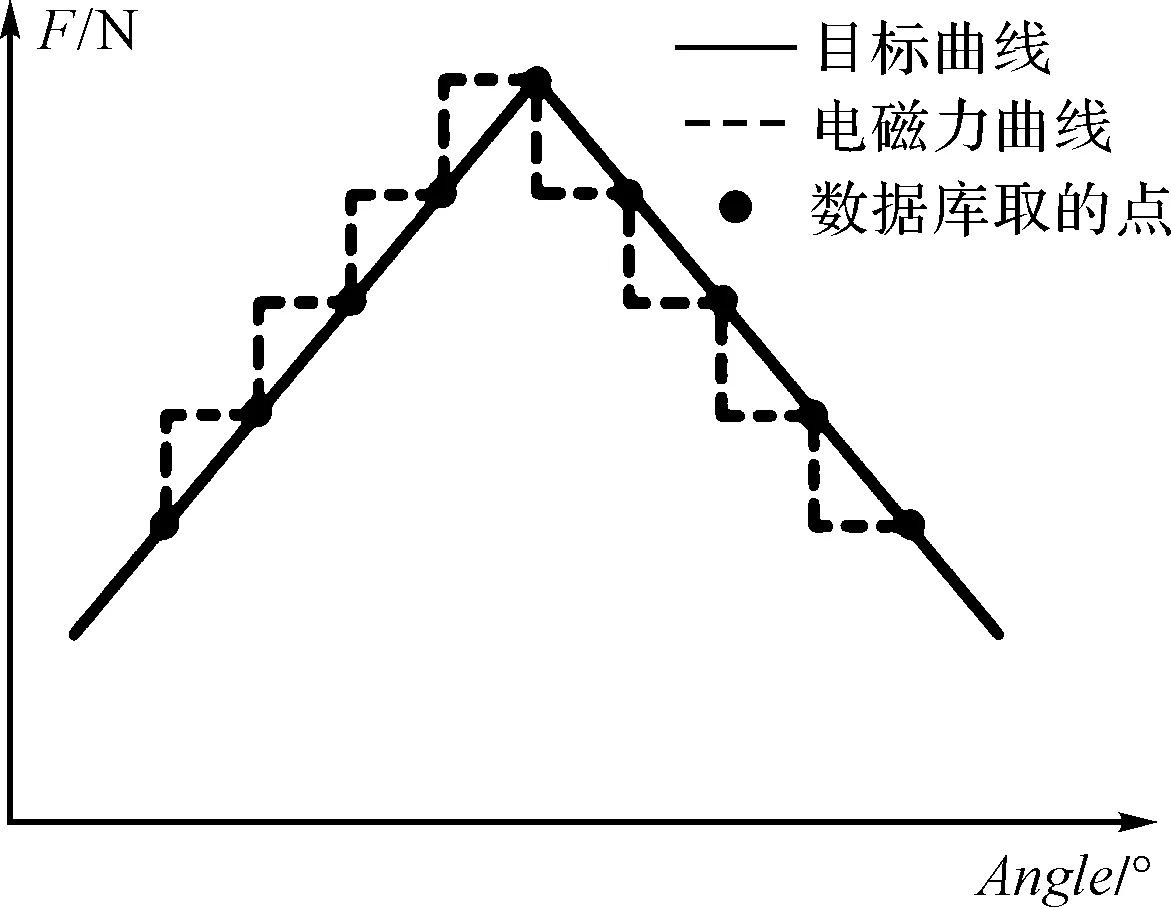
(b)略微过于提前
由于最小调整量是1个目标点距,使用单提前参数PID最优提前量平衡效果有2种情况,即上升和下降段总是存在一段略微提前,另外一段则略微滞后。
2.3 最优提前量不足原因分析
上述不足的原因是调整量至少为1个目标点距,难以实现图4中一般平衡效果,也无法实现图5中曲线1的密封效果;这是使用离散数据库的固有缺陷。
随着跟踪频率的上升,单位周期内总跟踪点数减少;电磁力曲线单侧滞后导致密封性不足,高频时因总跟踪点数较少,漏气趋势更明显。同时,图4中的一般平衡效果在高频时因过压余量不足,也存在漏气风险。
为达到最佳密封效果,此处以图5临界曲线1为目标;同时为确保电磁力始终略微大于轴向气体分离力,上升段提前步数略微大于下降段。因此,需要对文献[15]366-370中的算法及评价指标进行完善。就此,笔者提出一种累积误差结合误差方差的协同评价方法,及双提前量步数搜索算法。
3 方差和累积误差协同评价
3.1 以方差评价的平衡误差的特点
以方差作为平衡效果的评价依据,只能确定电磁力曲线和跟踪曲线较为接近,无法判断最优提前量平衡效果是略微提前还是略微滞后。
3.2 基于累积误差的平衡误差评价
累积误差的计算步骤如下:
(1)得到目标曲线上升、下降段转角范围,以便分别计算上升段累积误差和下降段累积误差;根据正、负斜率,将图1中的目标曲线切分为两个部分(上升段和下降段);设单位周期内目标曲线最小幅值处主轴转角为MinK,最大幅值处主轴转角为MaxK,则上升段主轴转角范围为[MinK,MaxK],下降段主轴转角范围为[0,MinK]和[MaxK,359];
(2)同步检测主轴转角和误差,根据主轴转角判断误差处于上升段范围还是下降段范围,分别计算其累积误差。此处设:
误差=Fa(K)-F(K)
(2)
式中:Fa(K)—目标平衡力,N;F(K)—电磁力,N。
在当前的跟踪频率下,设单位周期内经离散系统检测得出的位于上升段范围的主轴转角为Kn1,Kn2,…,Kni,位于下降段范围的主轴转角为Km1,Km2,…,Kmj;计算上升段累积误差的公式为:
(3)
式中:AllErr1—上升段累积误差,N/°;i—单位周期内上升段误差最大采样次数。
计算下降段累积误差的公式为:
(4)
式中:AllErr2—下降段累积误差,N/°;j—单位周期内下降段误差最大采样次数。
(3)由于高频时跟踪步数较少,跟踪误差增大,累积误差的计算也会有误差,此处将20个周期的累积误差取平均值。其中,上升段平均累积误差公式如下:
(5)
式中:AveAllErr1—上升段平均累积误差,N/°。
下降段平均累积误差公式如下:
(6)
式中:AveAllErr2—下降段平均累积误差,N/°。
累积误差指标评价效果为:
当平均累积误差=0时,是一般的控制效果。而实际因为调整量是按照整点距进行的,所以一般得到的是图6的两种效果。
平均累积误差>0时平衡效果如图7所示。

图7 平均累积误差>0平衡效果
电磁力总体小于轴向气体分离力,动、静涡盘分离趋势会随着平均累积误差的增大而增大,气体泄露程度也随之增大。
平均累积误差<0时平衡效果如图8所示。

图8 平均累积误差<0平衡效果
电磁力总体大于轴向气体分离力,动静涡盘接触趋势会随着平均累积误差绝对值的增大而增大,动静涡卷磨损程度也随之增大。因此,以累积误差作为评价平衡效果的标准,可判断出其过压或者密封性不足。
50 Hz跟踪累积误差和提前步数数据如表2所示。
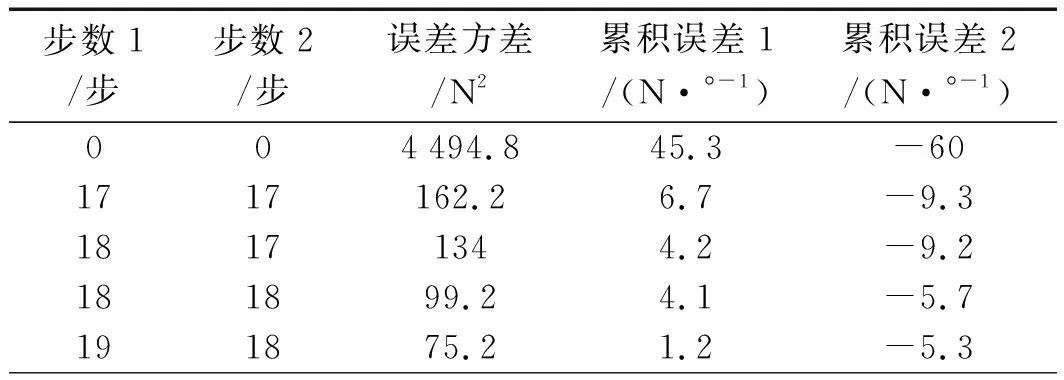
表2 50 Hz跟踪累积误差和提前步数数据

(续表)
步数1—上升段提前步数;步数2—下降段提前步数;累积误差1—上升段平均累积误差;累积误差2—下降段平均累积误差
表2中,上升、下降段提前步数均为19步,即单提前参数PID的最优提前步数;上升段平均累积误差为1.0,密封性略微不足,下降段平均累积误差为-1.3,略有过压;实际平衡效果如图6(a)所示。
不同频率以累积误差筛选得到的匹配值如表3所示。

表3 不同频率筛选得到的匹配值
步数1—上升段提前步数;步数2—下降段提前步数;累积误差1—上升段平均累积误差;累积误差2—下降段平均累积误差
表3中,以上升、下降段平均累积误差略微小于零为指标寻优,不同频率单位周期内会得到2个匹配值。
跟踪频率为300 Hz时,经筛选匹配到的两种平衡效果如图9所示。
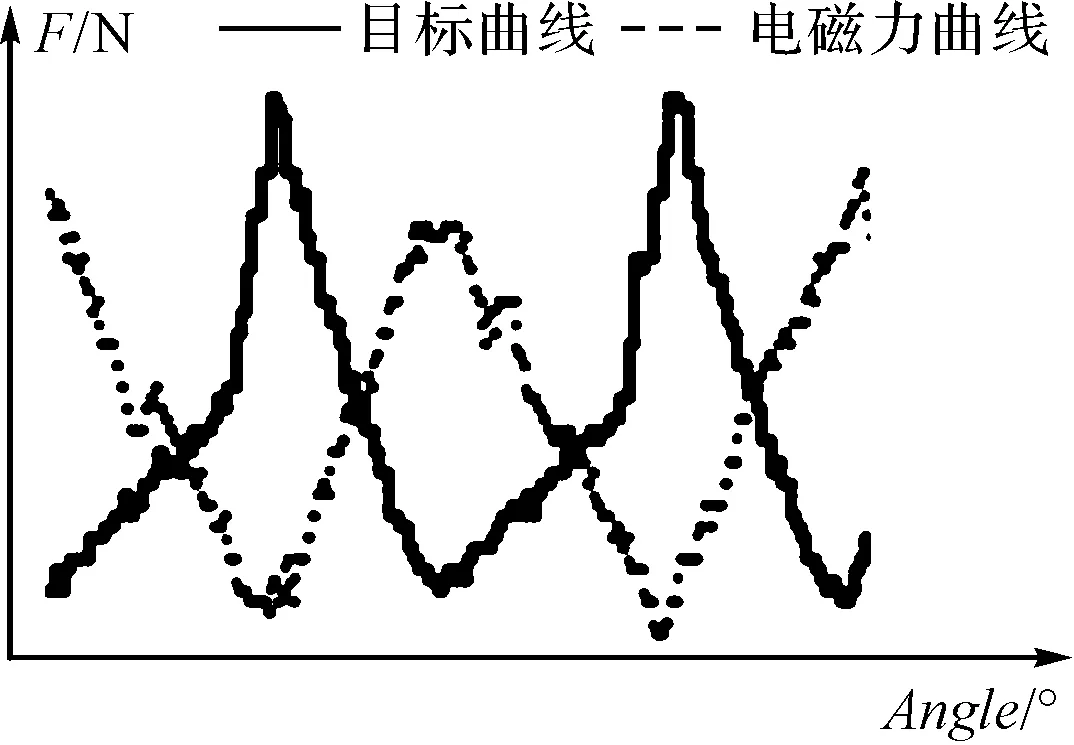
(a)上升段提前步数14,下降段提前步数13

(b)上升段提前步数174,下降段提前步数173
图9中,平衡效果上升、下降段平均累积误差皆为大小较接近的负值。因此,无法仅从累积误差来进行评价,需要结合误差方差指标来协同评价。
3.3 误差方差和累积误差协同评价
误差方差和累积误差协同评价可同时筛选出电磁力曲线较接近目标曲线,且满足平衡效果略微过盈的目标提前量,可排除提前量,筛选出最优提前量。
协同计算方法为:先初步搜索上升段和下降段的平均累积误差<0的提前量,再以误差方差为指标,进一步筛选出误差方差最小的提前量。
4 双提前量轴向动态密封算法
由于单提前量PID算法存在不足,笔者提出一种基于双提前量的动态平衡控制方法,并提出累积误差结合误差方差的协同评价方法。
4.1 基于双提前量的动态平衡控制
为提供更高的压力余量,确保电磁力略大于轴向气体分离力,设置上升段提前步数为略微大于下降段。
单提前参数PID算法与双提前参数PID算法提前步数的对比图,如图10所示。

(a)单提前参数PID跟踪目标
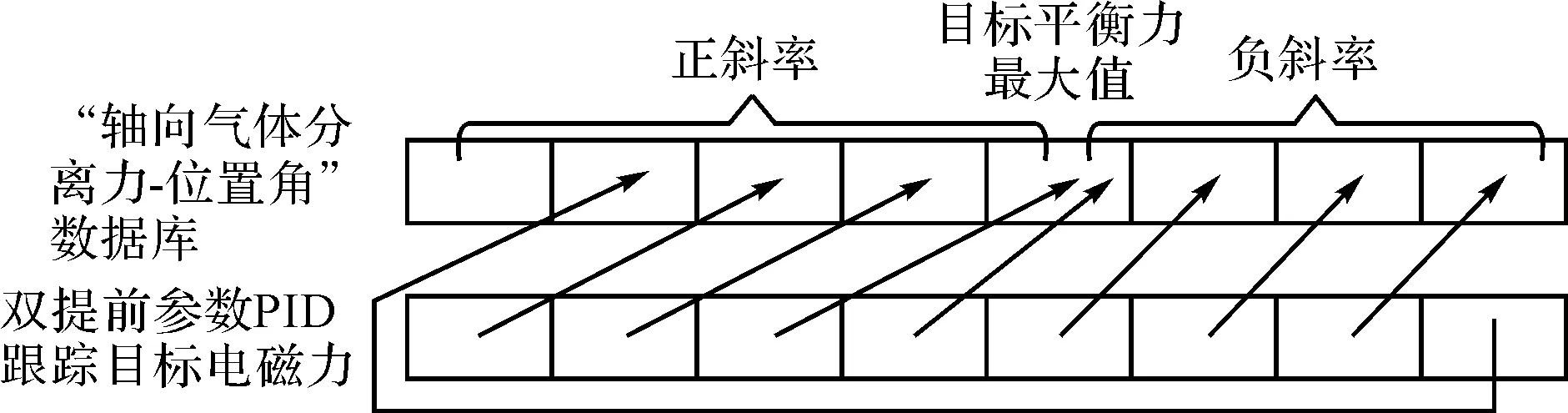
(b)双提前参数PID跟踪目标
设M=上升段提前步数-下降段提前步数。图10中,双提前量步数搜索算法会使总跟踪点数减少,跟踪误差变大,因此,M越小越好。
4.2 自适应轴向动态密封算法
基于双提前跟踪量的轴向动态密封流程包括:离线建立数据库和在线自适应跟踪。
双提前量离线数据库的建立流程如图11所示。
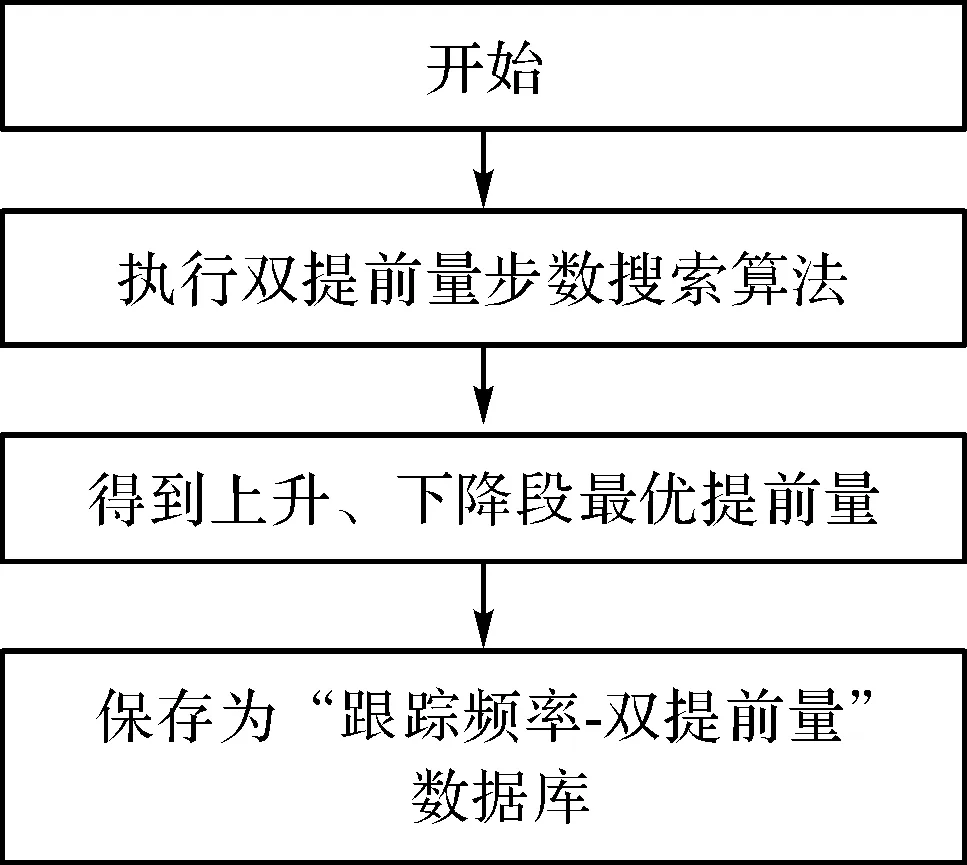
图11 双提前量离线数据库建立流程
离线数据库建立阶段目标是:采集各个跟踪频率下最优提前量,建立“跟踪频率-双提前量”数据库。
双提前量在线自适应跟踪流程图如图12所示。

图12 双提前量在线自适应跟踪流程
系统刚运行时,根据实时反馈的转速信号设置系统跟踪频率,根据跟踪频率查询数据库自适应匹配最优提前量。
4.3 离线双提前量步数搜索算法
双提前量步数搜索算法流程图如图13所示。

图13 离线双提前量步数搜索算法流程
4.4 基于双提前量的在线跟踪方法
双提前量在线自适应跟踪流程图如图14所示。
图14中,系统可实时获取当前主轴转角,根据主轴转角位于上升段还是下降段转角区间,匹配相应的提前量。

图14 双提前量在线自适应跟踪流程图
5 实验和结果分析
涡旋压缩机的轴向力电磁平衡方案,是以轴向气体分离力为跟踪目标,通过电磁吸力值来实时调整电磁线圈电流(电磁吸力),以平衡气体分离力,实现电磁力略微过盈状态下的压缩机动态接触密封。
笔者搭建了半实物实验平台(实验系统没有压缩腔,其余动态电磁吸力机构参数与完整系统一致)对方案进行模拟验证,如图15所示。

图15 半实物实验平台概况
模拟平台参数如表4所示。

表4 半实物实验模拟平台参数
笔者分别针对30 Hz,50 Hz,70 Hz,100 Hz,167 Hz,200 Hz,300 Hz不同跟踪频率进行了验证。各跟踪频率下的最优提前步数如表5所示。

表5 各个跟踪频率下寻优结果
步数1—上升段提前步数;步数2—下降段提前步数;累积误差1—上升段平均累积误差;累积误差2—下降段平均累积误差
跟踪频率为50 Hz时的平衡效果如图16所示。

图16 50 Hz平衡效果
平台200 Hz的平衡效果如图17所示。
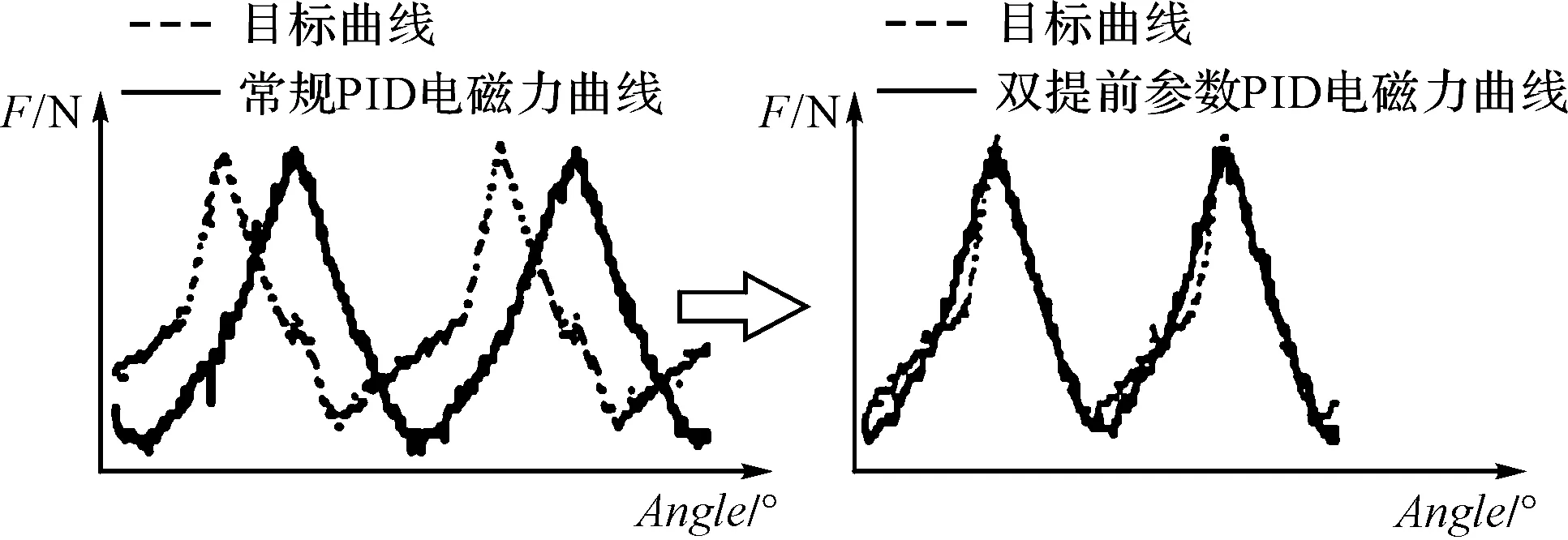
图17 200 Hz平衡效果
由图(16,17)结果可知:最优提前量随跟踪频率增加而增加;该算法可以针对不同跟踪频率自动寻优最佳提前量,增加系统密封性和稳定性。
6 结束语
为改善涡旋压缩机的轴向力动态平衡问题,进而改善涡旋压缩机的动态密封,笔者在电磁机构产生电磁力快响应动态平衡方案的基础上,对误差方差和累积误差评价的平衡特点进行了分析,针对单提前参数PID最优提前量平衡效果的不足,提出了以累积误差结合误差方差协同评价的双提前量步数搜索算法,并以半实物试验验证了压缩机的动态电磁平衡效果。
研究结果表明:
(1)以累积误差结合误差方差协同评价,不仅可以判断跟踪匹配程度,还可以判断出略过压密封状态或略欠压密封性不足状态;
(2)离线阶段,对不同跟踪频率,采用双提前量步数搜索方法同样可以较好地自动寻优提前步数;
(3)在线跟踪阶段,双提前参数动态平衡方法可以确保全程以略过盈压力状态实现更好的动态密封效果,高频时比单参数提前的优势作用更明显。
在后续的研究工作中,笔者将对不同跟踪频率下的最佳过压余量展开研究,以实现涡旋压缩机更好的动态密封效果。
