基于卷积神经网络的采煤机截割部减速器故障诊断研究*

2021-10-27包从望刘永志车守全

机电工程 2021年10期

关键词：峭度采煤机齿轮

包从望,江伟,刘永志,车守全

(六盘水师范学院矿业与土木工程学院,贵州六盘水 553000)

0 引言

采煤机作为综采工作面的关键设备之一,主要由截割部、牵引装置、行走装置及附属装置等部分组成。其中,截割部减速器的运行功率占整机功率的90%以上,且因运行工况恶劣,导致其故障频发。

为保障矿井的安全生产,提高采煤机的采掘效率及智能化水平,建立采煤机故障诊断模型,实现采煤机运行状态的实时监测尤为重要。然而,受采煤机恶劣工作环境的影响,如何精准快速地提取故障特征,对采煤机的前期故障进行智能诊断依然是难点问题。

近年来,国内外学者针对采煤机的截割部减速器故障诊断方法进行了大量研究。毛君等人[1,2]以油位、齿轮磨损量、温度等非振动信号作为诊断信号,基于深度自编码网络,建立了采煤机截割部减速器的故障诊断模型。刘旭南等人[3]采用ANSYS、ADAMS等分析软件,建立了采煤机截割部齿轮的裂纹、断齿、及轴承缺陷等故障模型,并基于小波包分解实现了对采煤机截割部传动系统的故障诊断。曹现刚等人[4]采用主成分分析法,结合遗传优化算法对BP神经网络的参数进行了优化,形成了基于PCA-GA-BP的采煤机故障诊断模型。LEI Si等人[5,6]基于多尺度模糊熵与支持向量分类模型,实现了对采煤机切屑状态的监测与故障诊断。郝志勇等人[7]利用销轴传感器实现了对采煤机截割部惰轮传动轴的载荷测量,从而完成了对惰轮轴的载荷监测。

目前,在人工智能高速发展的形势下,智能故障诊断也已广泛运用于机械运行状态监测。SYAHRIL R S等人[8]以有限数据样本,利用最优贡献度测量数据,基于层叠稀疏自编码器构建了齿轮箱的深度学习故障诊断模型。MOSLEM A等人[9]利用电机电流特征分析,基于多传感信息融合技术,构建了二维卷积神经网络下的齿轮箱故障诊断模型。史光宇等人[10]将轴承的振动信号变换为二维灰度图像,并基于卷积神经网络的训练,实现了对风电机组轴承的故障诊断。昝涛等人[11]将卷积神经网络由单输入层改进为多输入层,使模型具有更强的鲁棒性能,实现了对滚动轴承的故障诊断。WEI D等人[12]基于卷积神经网络,以较高的分类精度实现了对电压传输电路的故障诊断。吴春志等人[13,14]直接以齿轮振动信号作为输入,基于一维卷积神经网络,实现了对齿轮箱的故障诊断。

采煤机截割部减速器故障诊断的难点在于故障特征提取,准确的故障特征是实现故障分类的前提。卷积神经网络为典型的深度学习方法之一,具有较高的精度和鲁棒性,被广泛用于图像处理以及模式识别领域。

基于振动信号的时频分析方法可从不同角度提取截割部减速器的故障特征,但处理过程繁琐。将振动信号的时频分析方法与卷积神经网络相结合,可解决故障特征提取困难的问题;但传统方法中只是简单地将振动信号变为时域二维灰度图,变换过程中容易丢失频谱特性,且故障特征的准确性和重复性受采样时长的影响较大。

因此,在变工况下,笔者利用快速Kurtogram算法提取采煤机截割部减速器振动信号的谱峭度,并对谱峭度作像素归一、灰度变换等预处理,将结果输入至卷积神经网络,实现自适应特征提取,以解决传统方法中存在的不足。

1 CNN及快速Kurtogram算法

1.1 卷积神经网络(CNN)

作为深度学习的算法之一,CNN为一种前馈神经网络,在训练学习过程中不断改变各个神经元的权值和偏置。最早的CNN作为分类器在图像识别中有着广泛的应用。CNN结构如图1所示。

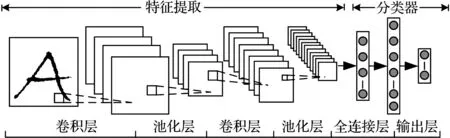
图1 卷积神经网络层次结构

其主要层次结构包括输入、卷积、池化、全连接及输出层。在CNN中,图像输入到网络中后,经多个卷积与池化层的计算实现特征的提取,不仅强化了特征而且还增强了网络的泛化能力。高纬度特征经全连接层与输出层的激活函数运算后产生一维特征向量,作为分类器的特征输入。

相比原始特征提取的方法,其无需关注特征的形状与强弱,经卷积与池化计算后即可将特征值保存在一维特征向量中。

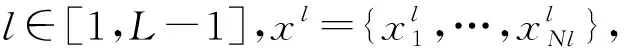
在卷积层,以上一层的特征图作为输入,并利用激活函数形成新的特征图,并输入到池化层,即:

(1)

常用的激活函数有Sigmoid和Tanh等非线性函数,其表达式如下:

(2)

(3)

因Sigmoid函数存在梯度丢失问题,笔者在此处采用Tanh函数。

池化层的作用是对卷积层中的特征图实现降维,可抑制卷积层中的过拟合问题。常见的池化方式有最大值与均值池化。池化层的计算如下:

(4)

式中:β,b—权值矩阵和偏置矩阵;down(·)—池化降采样函数。

当特征提取后,利用全连接层将相邻层的所有神经元相连,即将二维的特征图转化为一维特征向量。其模型计算如下:

O=f(b0+w0·fv)

(5)

式中:b0,w0—偏置矩阵和权值矩阵;fv—特征矢量。

1.2 快速Kurtogram算法

谱峭度可较好地反应冲击信号,常用于评价冲击信号的强弱[15，16]。采煤机的截割部减速器发生故障时,其所产生的信号可看作冲击不平稳信号,可用快速Kurtogram算法提取其谱峭度,过程如下:

(1)构建低通滤波器h0(t)和高通滤波器h1(t),即:

h0(t)=h(t)ejπt/4(f∈[0,1/4])

h1(t)=h(t)ej3πt/4(f∈[1/4,1/2])

(6)

式中:h(t)—截止频率为1/8的低通滤波器。

快速Kurtogram分解层次如图2所示。

图2 快速Kurtogram分解层次

根据谱峭度的定义,快速谱峭度图谱的计算如下式:

(7)

(3)经快速Kurtogram分解后,频率与频率分辨率之间的匹配关系如图3所示。

图3 快速Kurtogram结构图

在频谱提取过程中,可根据频率分辨的需要对分解层数进行延伸。

2 减速器故障诊断模型

采煤机截割部减速器的原始诊断信号为一维振动信号,而卷积神经网络的最大优点是对二维图像进行特征提取,因而无法直接将振动信号输入到卷积网络。直接将振动时域信号的二维图像输入到卷积神经网络中,虽可以实现基本诊断功能,但对时域信号的时长有严格要求;且时间长度不一样将导致振动图像有区别,进一步影响故障特征的准确性和重复性。

采用快速Kurtogram算法,不仅可评价截割部减速器故障振动冲击信号的峭度指标和频谱特性,还可将一维振动信号变为二维图谱,以作为卷积神经网络的输入,进一步提取特征向量。

2.1 基于卷积神经网络的诊断方案

本文结合采煤机截割部减速器故障诊断需求,确定诊断方案如图4所示。

图4 采煤机截割部减速器故障诊断方案

首先,基于减速箱故障诊断实验台,笔者分别提取不同转速下的齿轮健康、疲劳点蚀、断齿、齿面裂痕、低磨损和高磨损几种振动信号,分别作为故障诊断模型的原始信号;并利用快速Kurtogram变换将时域信号变为谱峭度,将二维谱峭度图进行像素尺寸归一化处理后进行灰度变换,以灰度图的结果作为神经网络的输入;

然后，笔者以各状态的图谱作为卷积神经网络的输入,利用全连接网络分别对输入进行卷积计算和池化计算,以提取其故障特征;

最后，笔者利用分类器将故障状态分类,以识别率和特征提取的可视化效果作为网络模型的评价指标,判断所提模型的聚类效果与故障识别性能。

2.2 数据预处理

因采煤机截割部减速箱齿轮的原始振动信号为一维信号,为方便卷积神经网络的图像输入,笔者分别对5种齿轮状态下的一维振动信号进行快速Kurtogram变换,获取二维谱峭度,将谱峭度作像素尺寸归一化处理变为256×256后,作灰度变换。

笔者提取同一故障状态、不同工况下的齿轮箱振动信号对网络进行训练,以增强网络对不同工况的鲁棒性;设置采样频率为2 kHz,电机转速为500 r/min时,齿轮点蚀原始时域信号的预处理过程如图5所示。

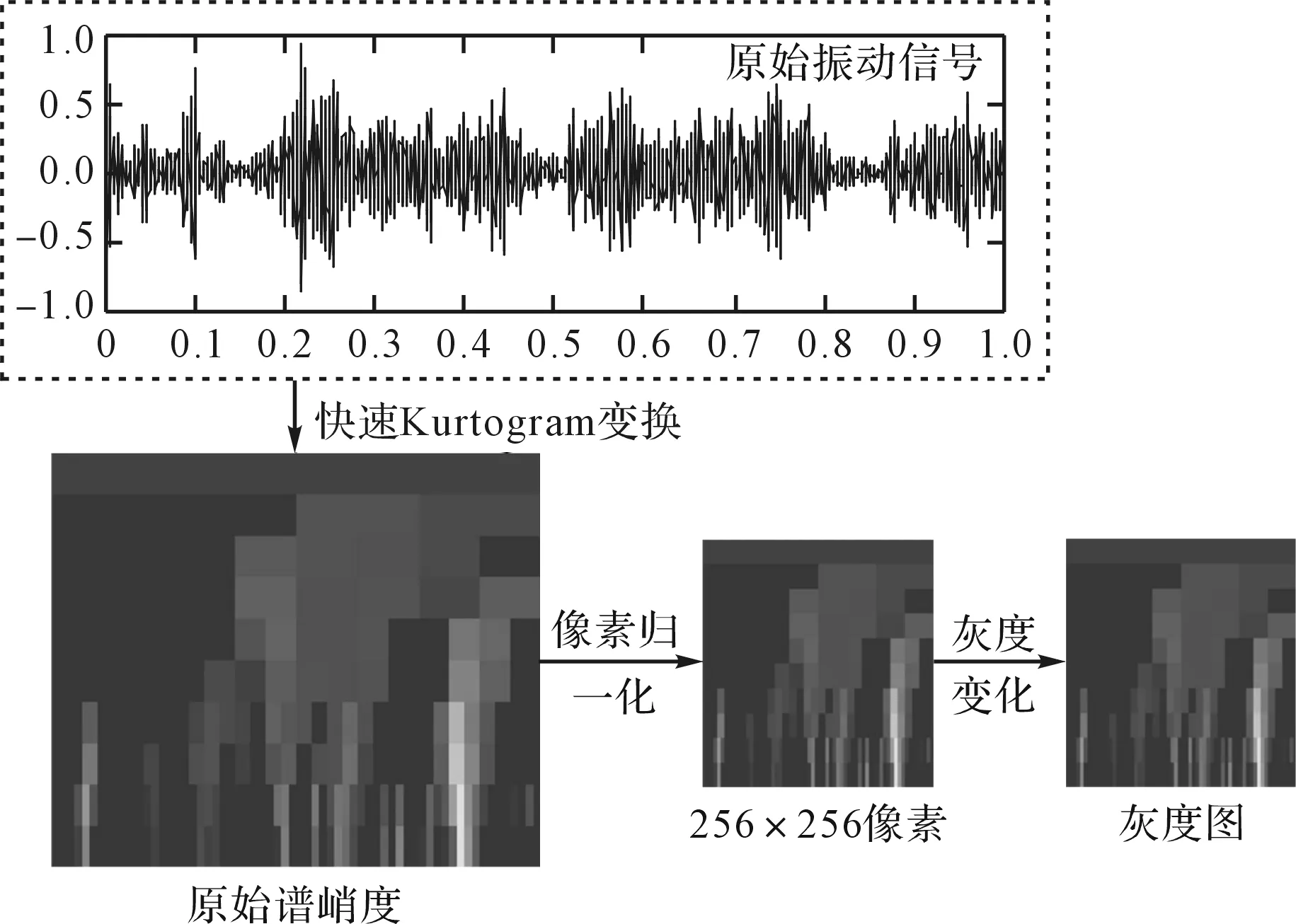
图5 齿轮点蚀数据预处理

2.3 卷积神经网络模型设计

该网络模型主要分为特征提取和故障分类识别两层。

笔者将归一化处理过之后的谱峭度(256×256)输入到卷积输入层,构建结构层数为2层的卷积-池化层对。

其中,第1、2卷积层的核大小分别取5×5,通道数分别为1、16,激活函数均采用tanh函数;池化层的核大小均取2×2,通道数分别为16、32;全连接层的通道数分别取为512、218。

3 实验及结果分析

3.1 实验描述

为验证所提采煤机截割部齿轮箱故障诊断的有效性,笔者结合某采煤机截割部减速器的结构原理搭建减速器实验台。

采煤机截割部的减速器一般有3至5级齿轮减速传动,为精确反映截割部减速器的故障信息,笔者所搭建的实验台可利用变速变换档位将传动在3、4、5级之间转换。该减速传动系统中,齿轮1到齿轮9的模数分别为9、9、9、9、9、14、14、14、14,齿数分别为19、34、34、23、46、17、28、28、39。

笔者将齿轮的尺寸同比缩减10倍,即模数分别变为1、1、1、1、1、1.5、1.5、1.5、1.5,齿数保持不变,由此构建的实验台如图6所示。

图6 截割部减速箱故障实验台1—变频电机;2—减速箱;3—变速变换档;4—振动传感器;5—数据采集器;6—速度控制箱

此处利用电火花加工方式,将齿轮的几种故障加工在不同齿轮上,齿轮的健康状况如图7所示。

图7 实验用齿轮健康状况1—健康齿轮;2—疲劳点蚀;3—重度磨损;4—轻度磨损;5—数齿面裂痕;6—断齿

笔者分别采集其振动信息。减速器可由速度变换档进行速度调节,实现不同速度下的故障验证。

实验过程中,振动传感器安装在减速箱外壳上,采用频率设置为2 kHz。笔者采用Tensor Flow平台对模型进行编程;计算平台的基本配置为Intel Core i7-10750和P2000-5 G GPU。

3.2 数据处理

实验过程中,笔者分别测取电机速度为500 r/min、800 r/min、1 000 r/min变工况时,齿轮运行的6种状态信息,每种速度下的样本数为200个,共600组数据,并将同一故障状态下不同速度所测取的振动信号进行序号打乱,形成故障数据集。

电机速度为500 r/min时,齿轮在各种状态下的时域振动波形图如图8所示。

图8 齿轮故障振动信号时域波形

图8中:N、P、HS、LS、CT、MT分别表示健康、疲劳点蚀、轻度磨损、重度磨损、齿面裂痕、断齿的情况。

上述情况所对应的谱峭度如图9所示。

图9 各类故障谱峭度

笔者在每种状态的数据集中选取400个和200个样本,分别作为模型训练和测试样本。数据集的组成如表1所示。

表1 齿轮故障诊断数据集

3.3 结果分析

为对比实验效果,笔者借助传统故障诊断方法,以振动信号的幅值、能量、偏度、标准差等作为故障诊断的特征值,利用SVM作为分类器,将故障诊断的识别率与所提的故障诊断模型进行对比,其方法描述如表2所示。

表2 不同齿轮故障模型描述

笔者将不同方法所提取的特征值运用t-SNE降维算法实现特征学习效果可视化对比。

笔者直接对原始振动信号进行t-SNE降维后的可视化结果如图10所示。

图10 原始信号特征t-SNE可视化

图10结果表明:原始信号之间存在较强的耦合性,无法区分齿轮的各个运行状态;尤其是5种故障信号之间,直接存在特征交融的状况,因此无法直接将原始信号作为故障识别的特征值。

笔者提取原始信号中的幅值、偏度、标准差、均值等作为故障特征,并对故障特征进行可视化处理,其结果如图11所示。

图11 信号基本特征t-SNE可视化

图11结果表明:原始信号作特征提取后具有一定的可分性,尤其是健康状态与故障状态之间存在明显的聚类效果,但各类故障特征之间依然存在相互耦合重叠的现象,不利于故障分类。

原始振动信号经EMD分解后,笔者提取各分量幅值、能量、偏度、标准差等特征值的t-SNE可视化的效果,如图12所示。

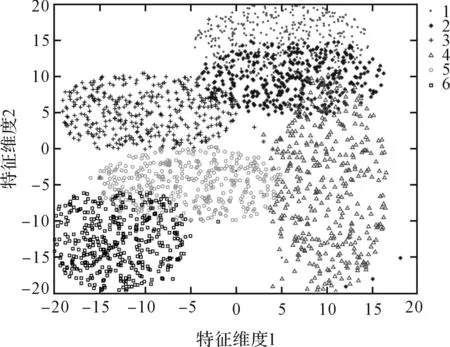
图12 EMD分解特征t-SNE可视化

图12结果表明:原始信号经EMD分解后,所提取的故障特征值聚类效果优于原始信号的特征,但各类故障状态之间依然存在耦合问题,影响故障的识别问题。

用所提方法将原始信号进行快速Kurtogram变换后,提取谱峭度图,并将谱峭度图输入到CNN网络,进行无监督学习提取故障特征,其结果如图13所示。

图13 CNN学习特征t-SNE可视化

图13结果表明:经CNN网络自适应提取齿轮的故障特征后,各类故障特征之间没有出现异类交叉的现象,这与分类结果基本吻合。

对比图(10～13)可看出:原始信号经所提模型训练后,有较好的特征聚类效果,且各类故障特征间的耦合问题得以解决,充分发挥了CNN在截割部齿轮故障特征提取的优势,可为故障智能诊断奠定基础。

为进一步验证所提模型的有效性,笔者将上述几种方法进行对比。笔者利用几种方法提取特征,以SVM作为分类器对故障模式进行识别,其结果统计如表3所示。

表3 截割部减速箱故障诊断方法对比

表3结果表明:ORI-SVM的识别率最低,AMP-SVM的识别率在ORI-SVM的基础上有所提升,最大可达62.9%;

EMD-SVM将振动信号通过模态分解后得到多组内蕴模态函数,并提取特征表现明显的前机组内蕴模态函数的峰值、标准差、偏度、能量、边际谱等作为特征向量的特征值;

该方法在原有的基础上提高了识别率,识别率均在86%以上,但特征提取过程繁琐,影响故障诊断的实时性。CNN-SVM基于卷积神经网络,利用快速Kurtogram提取振动信号的谱峭度,并将图作为卷积神经网络的输入,该方法在充分保留信号的时频特征的前提下,利用CNN网络在特征提取方面的优异特性,实现故障特征的提取。对齿轮点蚀、重度磨损、齿面裂痕和断齿的识别可达100%,其余的健康状态与轻度磨损的识别在99%以上,其识别率明显优于前3种。