基于渐进结构优化算法的桥梁找型工作研究

王 军，王 萍，冯昭亮

（1.西安市政设计研究院有限公司，陕西 西安 710068；2.内蒙古阿拉善盟公路运输维护中心，内蒙古 阿拉善盟750306；3.西安航天城市政公用发展有限公司，陕西 西安 710005）

0 引言

结构优化设计，通俗点说，就是选择较好的设计方案并进行设计。从广义上说，应当是用系统的、目的定向和良好标准的设计过程来实现对所选结构形式、外形尺寸、采用材料等的设计[1-2]。拓扑优化时，在限定条件较少，如尚不明确构件尺寸、构件之间的连接方式时，可以利用拓扑优化工具进行桥梁结构的找型工作，得到桥梁结构材料最优分布的桥型方案。

1 拓扑优化及其基本原理

优化设计按所选设计变量类型的不同可分为截面（尺寸）优化、形状优化和拓扑优化。其中，拓扑优化属优化设计的概念设计阶段。其目的主要体现在结构选型和结构布置上，即在满足各种约束条件下，去除不必要的构件和材料使结构在规定意义上达到最优，属于优化设计的最高阶段，难度也最大。因此，拓扑优化才是真正意义上的创造结构[3]。

对于设计人员，只要将有限元分析软件与优化设计方法结合起来，并把工程实际问题合理地转化为优化模型，就可以利用相关计算方法很好地完成优化设计。借助ANSYS 软件强大的优化分析功能，能够很好地完成既定的优化目标。ANSYS 的优化模块中三大优化变量为设计变量、状态变量、目标函数[4]。

1.1 设计变量

在结构优化设计方案诸多变量中，可以变化的量为设计变量。通过不断改变其值而逐渐得到最终的优化结果。ANSYS 分析软件最多可以定义60 个设计变量。

1.2 状态变量

状态变量为设计变量的函数，也可以独立于设计变量。状态变量必须满足一定的约束条件。约束条件可以是等式或不等式。避免状态变量的上限和下限取值过于接近，造成无解现象。ANSYS 分析软件中最多可以定义100 个状态变量[5]。

1.3 目标函数

目标函数是要尽量减小的函数。它必须是设计变量的函数。在ANSYS 优化程序中，它总是以最小化为目标函数。如果实际工程问题中所求目标函数为极大值，可以通过取倒数来实现。ANSYS 程序要求优化过程中只能有一个目标函数。

2 渐进结构拓扑优化方法

2.1 拓扑优化方法

结构拓扑优化可分为离散型和连续型。目前，连续体结构为拓扑优化主要的研究对象[6-7]。连续结构拓扑优化常用的研究方法有均匀化法、变密度法和渐进结构优化方法（Evolutionary Structural Optimization，简称ESO）等。

ESO 是近年来兴起的一种解决各类结构优化问题的数值方法。ESO 技术自1992 年提出以来，在国际上反响很大[5]。该方法由于能够很好地与有限元程序进行对接，能够获得较可信的优化结果。该算法基本原理为：通过构建一定的准则（应力、位移/ 刚度、频率），将结构中那些低效的单元慢慢删除，通过不断地重复迭代计算，获得一个最佳的结构形式[8]。由于该方法所依据准则简单、物理概念明确，因此很快扩展到多工况、非线性、动力等复杂问题。

2.2 基于应力和刚度共同约束的ES O

绝大多数的工程结构在运行状态下都同时受到应力和位移两方面的约束控制。桥梁结构在正常使用状态下不仅要满足应力约束条件，还要满足挠度约束条件。所以，研究这类问题更有工程应用价值。

对优化结构进行有限元分析后，如果所求的单元位移灵敏度数较低，则表明需要删除较多的单元，单元的删除率也相应较高。如果所求单元的应力较低，则表明结构中有较多单元处于低应力状态，相应的单元删除率也会较高。

基于以上分析，在位移和应力两方面控制下的单元综合灵敏度公式可表示为[8]：式中：αi，z为单元综合灵敏度；为每个单元Von Mises 应力；为单元最大Von Mises 应力；αi为每个单元位移灵敏度数；αmax为单元最大位移灵敏度数。

由于αi，z的取值范围为0＜αi，z＜1，所以单元应力值和位移灵敏度数有相同的数量级，不会产生较大的计算误差。

以上所分析的都是结构在单工况下的优化问题。而桥梁结构通常会同时受到汽车荷载、人群荷载、温度荷载等作用。对于多荷载工况，单元的删除准则为：每一个工况都满足删除准则的单元才能被删除。通过式（1）可以很容易计算出在不同荷载工况下，每个单元的综合灵敏度数，…，将其中最大值定义为这个单元的综合灵敏度数，即：式中，k 为总工况数。

3 截面拓扑优化

3.1 单元模型的选取

对截面采用渐进优化算法时，首先是将其离散成数量可观的单元，使单元网格尽可能小，这样得到的优化结果越精确。单元网格的划分要在建模阶段完成。在优化阶段，总是对同一模型进行反复迭代计算。研究发现，最初选取的模型形状能否代表所要进行优化的截面尤为重要，它直接影响到优化的合理性和正确性。

截面的拓扑优化可以分为平面应力单元优化和三维实体单元优化。平面应力单元优化采用四节点矩形平面应力单元计算，相对比较简单。有时候可将一些复杂的三维实体单元优化问题简化为平面应变和平面应力问题，能获得较好的优化效果。

3.2 控制截面的选取

当构件受力并不复杂时，采用结构中具有代表性的截面，如受力最不利截面，对其进行优化，就能客观地反映结构真实的优化后形状。当结构受到复杂荷载作用时，可以选择多个控制截面进行优化，对不同控制截面的优化结果进行比较，从而得出最优设计。根据已有的设计经验，首先考虑矩形截面为其初始设计截面。可以采取由结构整体→局部截面→优化后结构整体这样一个循环迭代过程。

3.3 设计区域的选取

设计区域的几何布局是未知的，要通过拓扑优化来确定其具体的位置形状，所以该区域是可以删除的区域。在优化模型的建立时，对于设计区域的几何体，在划分单元时尽量选用较为简单的单元形状，以有利于减少迭代收敛的时间。

4 拓扑优化实例

4.1 二维平面单元拓扑优化典型算例

对于平面应力单元的拓扑优化，ANSYS 软件分别提供了两种拓扑优化算法。第一种是以获得结构刚度最大为目标的线性结构静力分析。第二种是以获得结构动态刚度最大为目标的模态分析。本算例为第一种形式。该算法的中心思想是结构在静力荷载作用下，在满足体积缩减量约束条件的情况下，使得结构刚度最大。该算法不考虑材料和结构非线性，将结构刚度最大定义为目标函数。

拓扑优化时，尚不明确构件尺寸、构件之间的连接方式。在这种限定条件较少的情况下，可以利用拓扑优化工具进行桥梁结构的找型工作。以下就是很好的典范。

4.2 模型的建立

在修建道路上需要建造一座钢拱桥。该桥所在的空间形状如图1 所示。长方形顶面两侧连接的是两侧道路，长方形下面的左右两端点是拱桥两个桥墩安装的位置点。钢材的弹性模量为E=2.06×105 MPa，泊松比μC=0.3。假设桥面上承受P=110 MPa 的均布荷载，要求体积减少70%的条件下寻找最合适的拱桥桥型。

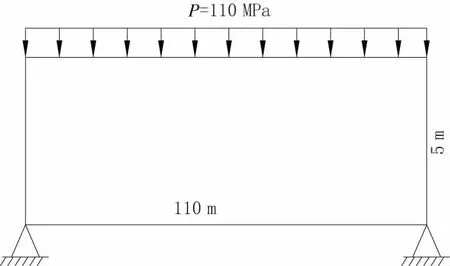
图1 初始设定拱桥空间形状

4.3 设计目标和约束条件

本例只有一个荷载工况，属于单荷载工况求解拓扑优化问题，如图2 所示。首先，将体积减少70%定义为约束函数。将施加在拱桥顶部的P=110 MPa荷载定义为拓扑优化函数。该函数也就是目标函数。

图2 拱桥截面拓扑优化区域及有限元模型

4.4 优化结果

由于要寻求拱桥最优的结构形式，必须有桥面部分的存在。要求桥面部分为本次研究长方形的顶部，即长方形的上表面单元必须保留，不参与拓扑优化迭代过程。所以，求解时将长方形顶层单元指定为非设计区域，其他单元指定为设计区域。

程序通过七次迭代，以获得结构最大刚度为最终目标，并通过设计变量给每个单元赋予内部伪密度来实现。

优化第一阶段，体积减小10%时，优化结果如图3 所示。

图3 迭代第一步优化图示

优化第二阶段，体积减小40%时，优化结果如图4 所示。

图4 迭代第四步优化图示

优化第三阶段，体积减小50%时，优化结果如图5 所示。

图5 迭代第五步优化图示

优化第四阶段，体积减小60%时，优化结果如图6 所示。

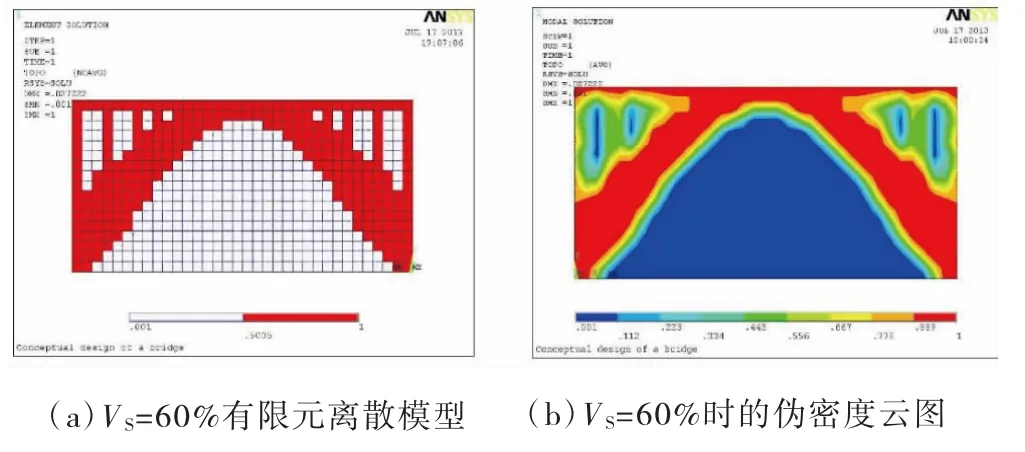
图6 迭代第六步优化图示

优化第五阶段，体积减小70%时，优化结果如图7 所示。

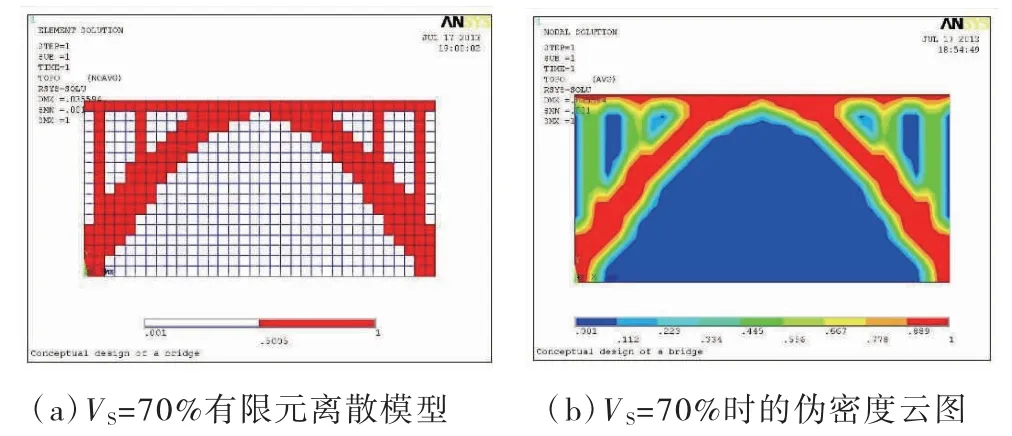
图7 迭代第七步优化图示

通过五次迭代，当体积删除VS=50%时，拱桥的桥型逐步显现；当体积删除率VS=70%时，能够清晰地显示出拱桥的桥型。此时迭代停止。在开始的几次迭代中，目标函数和体积变化比较明显，在经历了第16 次迭代后，优化结果趋于稳定，如图8 所示。

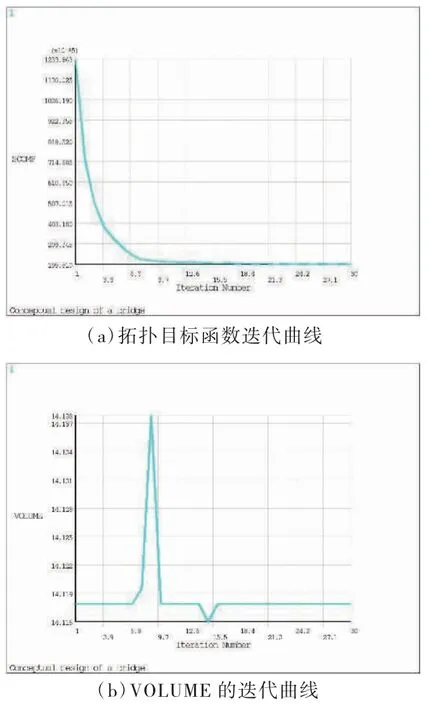
图8 目标函数、约束函数的迭代曲线

5 结语

拓扑优化时，由于尚不明确构件尺寸、构件之间的连接方式，所以可以利用拓扑优化工具开展桥梁结构找型的工作。本文算例是以单元刚度最大为优化目标的二维单元拓扑优化。经过数次迭代获得了较成功的拱桥桥型的优化结果，充分证明了采用ESO 法可以很好地开展桥梁的找型工作。