金刚石(001)面在Cu多种覆盖度下的稳定构型与电子特性

吴孔平，张 冷，王丹蓓，肖 柳，陈泽龙，张靖晨，张鹏展，刘 飞，汤 琨，叶建东，顾书林

(1.金陵科技学院电子信息工程学院，南京 211169； 2.南京大学电子科学与工程学院，南京 210093)

0 引 言

对金刚石表面进行处理来产生表面负电子亲和势已经引起研究人员的广泛兴趣[1-3]。金刚石的负电子亲和势(χ)是其导带最小值位于真空能级的上方，能大大地减小电子发射的能量势垒，即使在低温下导带电子也能跃迁至真空中[1-3]。结合金刚石优越的材料性能，负电子亲和势对金刚石在光阴极和热电子发射装置上的应用具有重要意义。目前，最广泛采取的办法是在金刚石表面上覆盖氢原子来产生表面负电子亲和势(χ)[4-5]。C—H表面化学键形成表面偶极子层，使得金刚石表面功函数由5 eV降低到3 eV[4]。

然而，尽管金刚石的功函数有所降低，但是对于低温热电子来说仍然太高，并且温度升高到500 ℃以上时，表面吸附的氢解吸脱附，导致金刚石的功函数显著增加[6]。其他的金刚石表面覆盖物，例如卤素[7]、氧[8]、碱金属卤化物[2]和碱金属氧化物[9]，也都被一一尝试过，这些研究表明：表面终端覆盖物都对金刚石表面电子亲和势产生一定的影响，要么功函数有所增加，要么在高温下是不稳定的。其中表面覆盖CsO时，金刚石表面产生了较低的功函数(～1.5 eV)，但是在377 ℃以上却表现出高度的不稳定性[10]。

对金刚石的界面设计与能带剪裁已经有了大量的探索与研究[11-13]，其中在Donnell 的工作中[11]，LiO覆盖金刚石表面产生了高达-3.9 eV的电子亲和势，从外延层的稳定性与负电子亲和势来考虑，LiO无疑是最佳的氧化物外延层。然而，Li与现代半导体微加工的工艺体系不兼容，而过渡金属却被广泛用来做肖特基或者欧姆接触。一个基于金刚石的有效电子发射器件，低的电子功函数与符合金刚石表面终端覆盖的热稳定性构型仍然没有完全确定下来时，过渡金属在上述诸多的物理性能方面就有很显著的作用。

而过渡金属铜(Cu)是半导体微加工中常见的一种过渡金属，通过溅射或者沉积技术，Cu常常被用作半导体的接触电极。相比近期计算的Al[14]，Cu电阻率更高、不易发生电迁移现象，在集成电路的互连技术中地位更突出。另外，Cu还常常被用来做散热片，这一点跟金刚石的高散热性能很相似。因此，金刚石跟Cu形成的界面引起了研究人员的广泛关注。再者，Cu通常不容易与金刚石形成碳化物，它很可能会在金刚石表面形成化学性质不活泼的突变结。近年来的实验研究表明，过渡金属Cu沉积在清洁的或者氧化的金刚石表面上[15-16]，都表现出非常好的热稳定性能，同时对金刚石表面的电子特性有着显著的影响。

在本文中，基于密度泛函理论并参考静电势平均的计算方法，克服了实验上对非故意杂质与缺陷研究的不足，在金刚石(001)表面使用过渡金属Cu作为表面终端覆盖物，并在不同的覆盖度下，计算出它们的表面原子吸附能以及稳定表面构型的电子亲和势。结果表明：除了会在金刚石(001)表面产生非常大的负电子亲和势(χ)以外，过渡金属Cu在金刚石表面还具有很强的附着力，这能为制备较好的热稳定、高效率的金刚石电极提供一定参考。

1 计算模型和方法

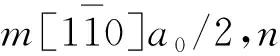
在结构优化的弛豫过程中，共轭梯度最小化方案被用于各个模型体系的结构优化。最终优化的结构中，对上面的四层原子进行自由弛豫来模拟材料的表面构型, 而底部两层原子固定在体材料中原子位置以保留体材料的结构特征。另外，各表面模型采用了6×6×1布里渊区网格，通过Monkhorst-Pack (M-P)自动产生匹配的不可约K点的方案[19]。最终使得体系中每个原子所受的力小于10-4eV/nm以及总能量小于10-5eV作为收敛标准。在计算轨道投影的态密度时，布里渊区使用了13×13×1的K空间网格密度。

计算表面的电子亲和势时，使用的是“bulk plus lineup”方法，是一个标准的计算过程[20-21]，通过位置函数的静电势与真空能级相比块体的金刚石而言，确定价带顶到相应静电势的位置。然后，使用金刚石实验的带隙值(5.5 eV)来确定相对价带顶的导带底的位置，从而克服了由于第一性原理计算半导体带隙偏低的弊端。通过这种方法，测试了金刚石常见的几种表面终端物覆盖后的电子亲和势，这些结果与实验值符合得非常好。尤其是对于氢(H)终端金刚石表面的计算，计算的结果与以前的理论计算结果也非常一致[22]。

平衡体系中每个表面Cu原子的平均吸附能(EA)定义为：

EA=(ET-ES-nμx)/n

(1)

式中：ET为金刚石表面被过渡金属Cu原子覆盖后的结构总能量；ES为金刚石清洁表面的总能量；n为表面Cu原子的总数量；μx为过渡金属原子自由状态下的能量。为了获得可靠的单原子能量，通过计算固体金属能量与实验内聚能相结合的方法来确定单个自由金属原子的能量。

2 结果与讨论

2.1 Cu多种覆盖度下的稳定构型

为了明确所研究体系潜在的平衡结构，在Cu覆盖金刚石表面时， Cu所占的高对称位置都被标记出来。过去Jia等[23]和谢希德等[24]曾经对金刚石2×1-(001)重构表面吸附其他金属开展过相关研究，根据他们的假设与研究结果，标记出Cu所占据的四个高对称点位置如图1所示。图中B表示桥位(bridge site)，处于第一层二聚化C-C化学键的中心；C表示洞位(cave site)，H表示谷桥位(hollow site)，P表示鞍位(pedestal site)。

图1 金刚石2×1-(001)重构表面可能的四个吸附位置，其中灰色的圆球表示C原子，大、中、小不同尺寸表示第一层、第二层和第三层中的C原子Fig.1 Four different adsorption sites are shown in the diamond 2×1-(001) surface. The C atoms are indicated by the gray ball, and the different sizes of big, medium and small represent the C atoms in the first, second and third layers

此外，为了全面深入评估表面结构的稳定性，在覆盖度1 ML时，测试了除上述四个位置之外的悬挂位置。该表面构型非常类似氢化金刚石重构的2×1-(001)表面。测试表明，该表面构型相比上述四个位置明显具有相对较高的能量，因此，该构型被认为是相对不稳定的，下文计算中不再考虑。

由于Cu在金刚石重构的2×1-(001)表面上存在多种覆盖度，依据图1所示的四个高对称点位置，根据覆盖度的定义可以得出0.25 ML、0.5 ML和1 ML三种覆盖度。本文的目标是要找出这些不同覆盖度下表面的可能稳定构型，尤其是低覆盖度(0.25 ML与0.5 ML)下表面的稳定构型。因为低覆盖度下，Cu在金刚石2×1-(001)表面上位置更具多样性。例如，对于0.25 ML来说，表面重构的原胞可以是4×1、2×2、4×2等类似结构。在金刚石表面测试Cu的0.25 ML下的稳定构型时，这三种表面重构的原胞都包括在内。在计算并判断各种覆盖度下的稳定构型后，计算出各个稳定构型的电子特性，如能带、表面电子亲和势。

在Cu的有机金属化合物中，Cu与C之间的相互作用较弱。在上述四种高对称点中，B位与C位最有可能成为Cu低覆盖度下的稳定构型，因为这两个位置具有最低的Cu跟C之间的相互作用。首先对单Cu吸附表面进行测试计算。测试计算结果表明：Cu处于B位时，每个Cu原子的吸附能为-1.17 eV；Cu处于C位时，每个Cu原子的吸附能为-1.55 eV；另外Cu原子处于H和P位置时，每个Cu原子的吸附能为-0.97 eV和-1.22 eV。根据计算的单个Cu原子的吸附能，就可以判断出Cu处于C位最稳定，Cu处于其他的位置都属于亚稳定构型。

随后对多种构型进行全面的测试，对应每一种覆盖度下的所有构型中，选出其中三个Cu吸附能相对较低的构型，并把它们的位置构型、平均吸附能以及键长的计算结果列举在表1中，表中覆盖度1 ML时，C-Cu平均间距0.195(B)表示表面层的C同处于B位置的Cu之间的平均距离为0.195 nm。

表1 金刚石2×1-(001)表面在Cu覆盖度为0.25 ML、0.5 ML与1.0 ML三种情况下三个Cu平均吸附能相对较低的构型特性Table 1 Characteristics of the configuration with the relative lower average absorption energy (EA) for diamond 2×1-(001) surface under Cu coverage of 0.25 ML, 0.5 ML and 1.0 ML

根据表1中的计算结果，C-Cu平均间距大致分布在0.192～0.223 nm，Golubeva等[25]在Cu的有机化合物中研究得出C-Cu平均间距大致分布在0.197～0.216 nm，该项研究结果同本文的研究结果基本上是一致的。最重要的是在本文中得出Cu在0.25 ML和0.5 ML覆盖度下，Cu都是处于C位置达到最稳定的构型，对应的单原子吸附能分别为-2.12 eV和-2.46 eV。而Cu在覆盖度为1 ML下， Cu处于B和C位置时，覆盖的金刚石表面是最稳定的构型，这些稳定的构型如图2所示。此外，从Cu单原子的吸附能上还能够看出：随着表面Cu原子的覆盖度增大，单原子的平均吸附能减小，促进表面构型的稳定。表明Cu的增加，Cu与Cu之间形成的金属键有助于吸附表面的稳定。

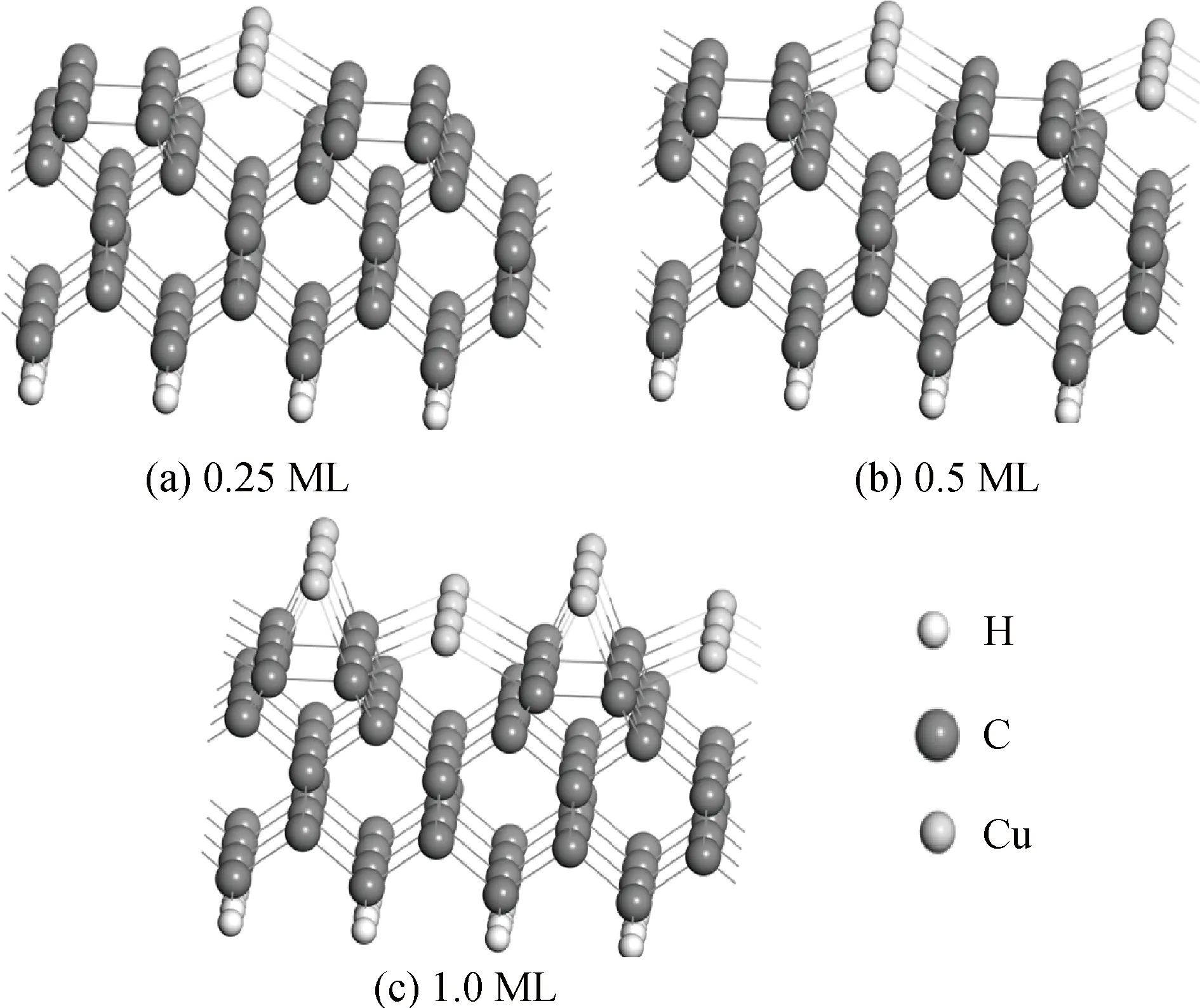
图2 金刚石2×1-(001)表面在不同Cu覆度的稳定构型Fig.2 Stable configurations for diamond 2×1-(001) surface under different Cu coverages

2.2 多种覆盖度下稳定构型的电子特性

图3(a)、(b)与(c)显示的是覆盖度0.25 ML、0.5 ML与1.0 ML三种表面结构的能带结构和总态密度。每个图的左半部分是能带结构，右半部分是对应的总态密度。图中0 eV处的虚线表示Fermi能级，另外，能带图中作为背景的点线区域为金刚石块体的能带图，可以看出，计算的金刚石带隙值为4.1 eV，这跟其他理论计算结果严格一致。

图3(a)显示Cu覆盖度0.25 ML下的表面能带结构，能带中在0 eV附近存在部分占据的能级，主要是由Cu的d轨道态与金刚石表面C的类π*态所形成的成键态所致，而在1.5 eV到3.0 eV附近完全空的能级主要是由Cu的d轨道态与金刚石表面C的类π态所形成的反键态所致。对于图3(b)中显示的Cu覆盖度0.5 ML下的表面能带结构来说，在0 eV的部分占据能级和1.3 eV到3.0 eV之间完全空的能级跟覆盖度0.25 ML下的金刚石表面能带结构完全类似。图3(c)显示Cu的覆盖度1.0 ML下的表面能带结构，存在大量占据态能级与非占据态能级在金刚石价带顶之上，在0 eV附近的部分占据能级与在1.5 eV附近非占据的能级对应Cu的局域d轨道，1.8 eV到3.0 eV之间的空能级对应C与Cu之间的杂化轨道。对于低覆盖度下，有相对较少的能级存在金刚石的带隙内。

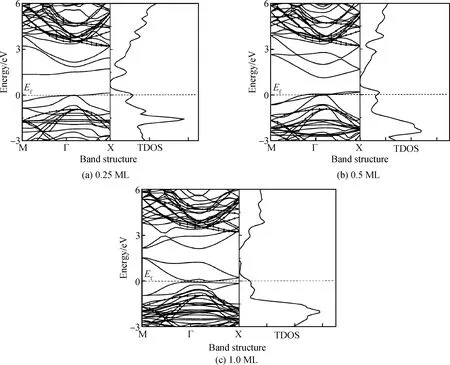
图3 金刚石2×1-(001)表面在不同Cu覆盖度下的稳定构型对应的能带结构(左)与总态密度(TDOS，右)。点画线为块体金刚石的能带结构，横虚线为Fermi能级Fig.3 Band structure (left) and total density of states (TDOS, right) of the stable configurations for diamond 2×1-(001) surface under different Cu coverages. The dot line indicates the energy band structure of the bulk diamond, and the horizontal dashed line is Fermi level

为了更清晰地认识表面Cu与金刚石表面C原子之间的相互作用，表面原子的投影态密度通过平均的方式被计算，也就是同一层同一类原子的总态密度除以该原子的数量，结果如图4所示。图4(a)、(b)与(c)分别显示了覆盖度为0.25 ML、0.5 ML与1.0 ML三种情况下金刚石表面原子的投影态密度。原子层数采取从表面原子层向体内原子层计数的方式。图4(a)、(b)与(c)三个图都表示，随着原子层的深入，C原子2p轨道电子特性逐步恢复金刚石块体特性，同时，计算结果中的Cu 3d轨道也都与表面C原子2p轨道电子产生杂化。特别地，在覆盖度1 ML时，B位的Cu和C位的Cu在Fermi能级处的3d轨道电子特性差别并不明显，但相比覆盖度0.25 ML和0.5 ML的C 2p轨道电子特性来看，从第一层到第四层C 2p轨道电子都在带隙内产生大量的表面态，表明更多的Cu覆盖金刚石表面，不仅会有Cu与金刚石之间的相互作用，同时也存在大量的Cu 与Cu之间的金属键。

图4 金刚石2×1-(001)表面在不同Cu覆盖度下稳定构型的投影态密度。Fermi能级位于0点,图中的原子层数从界面处开始计算Fig.4 Projected density of states (PDOS) of the stable configurations for diamond 2×1-(001) surface under different Cu coverages. The zero energy corresponds to the Fermi level, the number of atomic layer is counted from the interface

本文将采用“bulk plus lineup”方法来计算Cu覆盖金刚石表面的电子亲和势，该方法在最近的研究论文[26-27]中有详细的描述。图5显示了静电势随垂直表面方向上的位置变化关系，根据“bulk plus lineup”方法，很容易确定了价带顶(EV)和导带底(EC)的位置，以及相对于真空能级之间的相对能量位置，因此可以算出Cu覆盖金刚石表面的电子亲和势(χ)。同时，采用金属Cu功函数(ΦCu)的实验值5.16 eV[28]，可以根据Schottky-Mott模型来计算出金属Cu与金刚石接触的肖特基势垒高度(ΦBH)[29]:

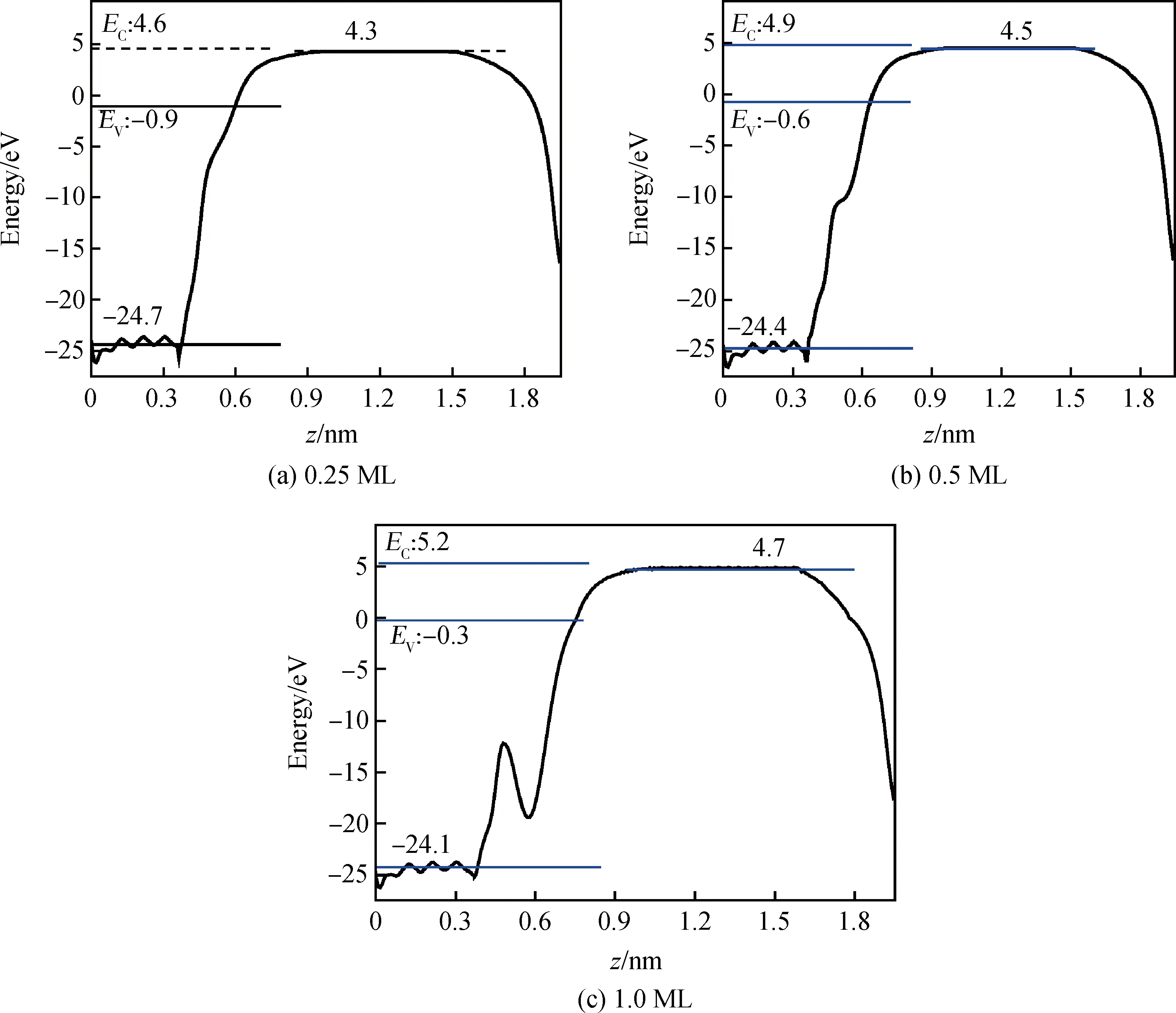
图5 针对金刚石2×1-(001)表面在不同Cu覆盖度下的稳定构型，沿着垂直表面方向上晶面振荡特性的静电势平面平均与位置之间的变化关系，导带底(EC)、价带顶(EV)与真空能级也标记在图中Fig.5 For the stable configurations of the diamond 2×1-(001) surface under different Cu coverages, the planar average of the electrostatic potential is as a function of the position along the direction perpendicular to the surface, and conduction band minimum (EC), valence band top (EV) and vacuum level are also marked in this picture

ΦBH=EG-(ΦCu-χ)

(2)

这里的金刚石带隙(EG)采用了实验值5.5 eV。

根据导带底相对于真空能级之间的相对能量位置，可以根据图5(a)得出覆盖度0.25 ML的金刚石表面电子亲和势(χ)为-0.3 eV，相应的肖特基势垒高度(ΦBH)为0.04 eV。根据图5(b)和5(c)得出覆盖度0.5 ML的金刚石表面电子亲和势(χ)为-0.4 eV，肖特基势垒高度(ΦBH)为-0.06 eV;覆盖度为1.0 ML的金刚石表面电子亲和势(χ)为-0.5 eV,肖特基势垒高度(ΦBH)为-0.16 eV。根据不同覆盖度下表面电子亲和势(χ)的计算，获得了各种覆盖度的Cu终端金刚石表面电子亲和势(χ)和对应的肖特基势垒高度(ΦBH)，并将它们反映在图6中。图6采用了金刚石没有任何覆盖下的表面电子亲和势的实验值0.75 eV[30]，根据这些值与Cu覆盖度的变化关系，得出：Cu终端金刚石表面电子亲和势(χ)与对应的肖特基势垒高度(ΦBH)跟表面吸附Cu的覆盖度并没有非常强的依赖关系。

图6 金刚石(001)-2×1表面在不同Cu覆盖度下的电子亲和势 (χ)与肖特基势垒高度(ΦBH)Fig.6 Electron affinity (χ) and Schottky barrier height (ΦBH) for the diamond 2×1-(001) surface under different Cu coverages

而在实验上，Cu与金刚石的接触界面也是非常受重视的，Baumann等[29]通过沉积技术获得Cu与金刚石的接触界面，并结合紫外光电子能谱与场发射测量技术，获得Cu终端金刚石表面的电子亲和势与接触势垒高度，在他们研究结果中，Cu终端金刚石表面的电子亲和势为-0.2～-0.4 eV，测得肖特基势垒高度小于0.2 eV，这个结果跟计算的结果相比略大一些，这个很可能跟实验中非故意杂质有关，比如氧(O)的引入，必然导致电子亲和势与肖特基势垒的提升。

3 结 论

在Cu的低覆盖度下，Cu在金刚石表面占据洞位(C)最稳定，而在Cu的高覆盖度下，Cu在金刚石表面占据桥位(B)和洞位(C)最稳定，这时金刚石带隙中的电子态或者跟Cu的局域3d电子轨道相关，或者跟Cu3d电子轨道与表面的C 2p之间成键相关。此外，在金刚石(001)表面单层覆盖过渡金属Cu的方法，可以使金刚石表面具有较大的负电子亲和势，大小约为-0.5～-0.3 eV，肖特基势垒高度为-0.16～0.04 eV，这些理论结果与实验结果基本一致。尽管如此，实验上在金刚石表面沉积亚单层过渡金属Cu依然具有较大难度，原子层沉积技术有望解决这一难题，毕竟过渡金属Cu覆盖金刚石不仅具有稳定的碳化物表面构型，而且在负电子亲和势器件和特定物理功能器件方面有着重要的应用。