广义Markov跳变系统在一般转移率下的鲁棒无源控制

李秀英，牛冬平

近年来，广义Markov跳变系统的研究成为了控制领域的热点，其中包括稳定化控制器设计、H∞控制、耗散控制等［1−4］.众所周知，转移率是决定Markov跳变系统性能的关键因素.然而，在实际系统分析中，获得系统全部转移率信息是很难实现的，于是转移率部分未知情形受到了关注［5−6］.尤其研究系统具有一般转移率即转移率具有不确定性且部分未知情形［7］具有更加重要的实际意义.

无源性是系统控制理论中的一个重要概念，它在系统分析与控制中有着重要作用［8−10］.本文研究一类广义Markov跳变系统在一般转移率下的无源控制问题.给出了上述系统随机容许且无源的充分条件，进而设计状态反馈无源控制器使闭环系统是随机容许且无源的.

本文中，矩阵X>0（或X<0）表示矩阵X是正定的（或X是负定的）.ε{}⋅表示数学期望.∗表示对称矩阵中相应位置的转置.对于矩阵M，He(M)=M+MΤ.

1 预备知识

给定概率空间(Ω,F,P)，考虑如下一类Markov跳变广义系统：

为方便起见，对任意的rt=i∈S,系统矩阵分别简记为A i,B i,C i,F i,D i.

2 无源性分析

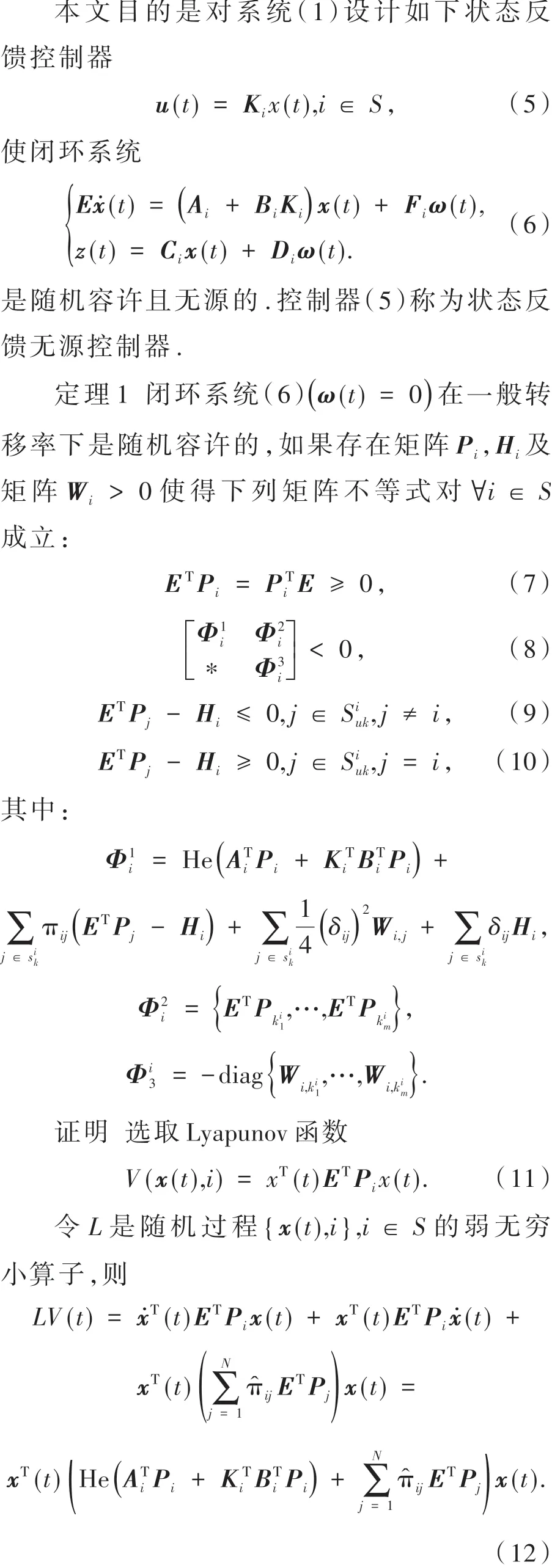
3 无源控制器设计

下面给出无源控制器设计方法，给出如下定理：

定理3给定γ>0，闭环系统（6）在一般转移率下是随机容许且无源的，如果存在矩阵X i，Y i，H i及矩阵Pˉi>0使得下列线性矩阵不等式对∀i∈S成立：

得到，根据Schur补性质知式（24）与式（19）等价，式（25）与式（20）等价，结合定理2的证明，于是定理3得证.

4 结语

本文研究了一般转移率情形下随机广义Markov跳变系统的无源控制问题.首先给出了系统在一般转移率条件下随机容许且无源的条件，进而得到了状态反馈无源控制器设计方法.控制器可通过求解相应LMIs得到.本文的研究工作丰富了已有的广义Markov跳变系统的控制理论成果.