基于Midas仿真优化的苏州河泄流孔加固结构设计优化分析研究

司黎晶，何妙妙，冯淑琳，王子凯

（1.镇江市工程勘测设计研究院有限公司，江苏 镇江 212003；2.吴中区水务局，江苏 苏州 215104）

水工结构设计水平决定了工程安全稳定运营的长久性，而水工设计需经多次优化，获得最佳设计方案，取得最适配工程的设计参数，工程竣工后运营安全与成本才属最优。为此，李宁霄、施得兵等、陈斌等利用物理模型试验理论，按照实际工程设计方案进行原模复制，在室内建立水工模型，加以相应的运营工况荷载，完成结构设计方案的比选优化，为工程设计提供实践参考。另有一些学者参照已有工程设计方案，基于现有工程的长期运营监测，判断设计方案利弊性，综合考虑拟建工程的适用性，这也是工程设计优化的一种重要手段。无论是物理模型试验方法还是运营监测已有工程方案，比选优化成本较高、周期较长，因而数值仿真手段逐步得到广泛应用。宁威锋、杨海全、庞敏敏利用ABAQUS、ANSYS 或者 COMSOL 多物理场仿真平台等，完成有限元模型静、动力场特征计算分析，进而获得设计参数与水工结构间关系，最终判断适合水工结构的最佳方案。本文根据苏州河口下游泄流闸孔钢加固结构设计优化问题，利用Midas 仿真平台进行设计方案优化分析，为工程设计提供计算依据。

1 工程仿真

1.1 工程概况

为提升苏州河下游泄流能力，河口建有一泄流闸，承担着地区防洪、排涝及水位控制作用。目前，水闸最大工作流量285 m3/s，闸前泥沙淤积较严重，河水最大含沙量达8.5 kg/m3，水闸运营畅通性受限较严重，闸门最大开度仅为原设计的65%，闸室底板高度由原26.5 m 降低至21.8 m，水闸工作能力及性能均受削弱。根据分析得知，该水闸闸顶高程为65.8 m，为多孔式泄流设计，布设有宽度6.8 m 的拦污栅，采用预应力闸墩作为支撑结构。原设计单孔泄流量155 m3/s，泄流孔净宽2.8 m，采用弯拱式结构，以排柱作为支撑系统，拱脚与拱顶长度为1.8 m，截面最大高度差为0.4 m。采用弧形钢闸门，直径2.6 m，有限元模拟计算结果表明该闸门静力工况下最大位移15.8 mm，抗滑移能力较弱。由于运营年限较长及上游泥沙淤积严重，河口水闸出现水流紊动，局部泄流孔出现险情，经运营水位下模拟计算得知，泄流孔中水头压力分布变化较大，局部易出现涡流等现象，渗流场较活跃，对水位调度、水流控制等均带来较大影响，考虑对该泄流闸孔进行加固设计。根据模拟仿真计算得知，闸前拦污栅最大拉应力1.85 MPa，以沉降方向位移最显著，可达15.8 mm，渗流场中浸润线可达栅墩中部，局部渗透坡降较高达0.35；而根据泄流孔水工结构动力响应计算得知，孔顶出现较大拉应力，超过2 MPa。闸孔中部渗流场较活跃，设计水位工况下浸润线高度位于孔侧壁中部位置，泄流闸孔平面如图1 所示。水闸泄流孔与闸门在静载下呈现较大变形、拉应力特征，对结构稳定性不利，工程管理部门考虑对河口水闸进行钢结构加固，在闸门及泄流孔壁设置连系梁钢结构，并开展优化分析，以提升水闸运营稳定性。

图1 泄流闸孔平面现状

1.2 工程仿真模型

为便于分析，给出河口水闸泄流孔加固后立面设计图，闸室地基视为刚体，加固钢结构截面设计为矩形，高、宽参数是设计优化重点，如图2 所示。利用Midas 仿真计算平台建立泄流孔加固后有限元模型，如图3 所示，划分网格共获得125 826 个微单元体，节点数85 684个。模型底部为多向约束，无自由度，而顶部为单向约束，仅有1个水平向自由度，上、下游均为自由边界，各部分结构物理力学参数均按照实际取值，岩土体参数按照地勘试验报告实测值。计算模型中X、Y、Z 正向分别为顺水流向、闸室垂直向上和水流横向右岸。基于上述工程资料与仿真模型，采用Midas 平台进行加固钢结构截面体型设计参数优化分析。

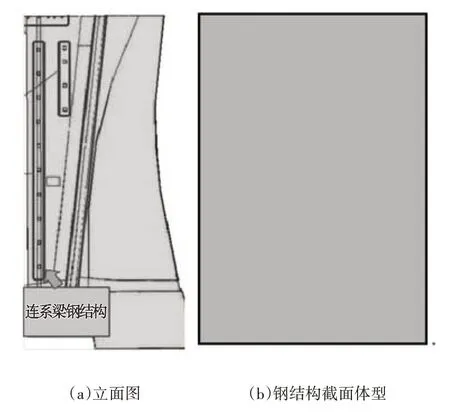
图2 河口水闸泄流孔加固后立面设计

图3 加固后泄流孔有限元模型

2 钢结构横梁高度设计参数优化分析

为分析钢结构横梁体型设计参数对泄流闸孔影响，在保证横梁高度不超过跨距1/4 前提下，设计横梁高度对比方案分别为1 m（A 方案）、1.1 m（B 方案）、1.2 m（C 方案）、1.3 m（D 方案）、1.4 m（E 方案）、1.5 m（F 方案），纵梁截面尺寸为1.2 m×1 m，横梁其他设计参数均保持一致，计算不同方案下泄流闸中闸门、泄流孔壁及纵梁3个关键部位应力特征。

2.1 拉应力特征

根据不同方案应力计算，获得横梁高度影响下最大拉应力变化特征，如图4 所示。

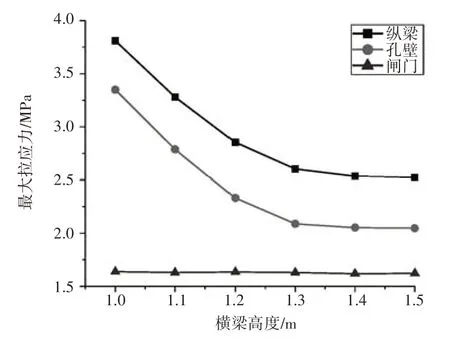
图4 横梁高度影响下最大拉应力特征

从图4 可知，3 个关键部位中纵梁上拉应力最大，在横梁高度1.1 m 方案中该部位最大拉应力可达3.3 MPa，而此时孔壁、闸门上拉应力相比前者分别降低了15%、46.7%。在各设计方案中纵梁拉应力与孔壁间差幅达13.7%～24.7%，与闸门上差幅达46.5%～1.2 倍，即改变横梁截面体型，结构张拉危险面易出现在纵梁部位上，应系统性协调横、纵梁体型，确保在加固钢结构中不出现潜在张拉破坏面。对比不同横梁高度参数设计方案中关键部位最大拉应力变化可知，纵梁、孔壁上最大拉应力随高度递减变化，在横梁高度1 m时孔壁上最大拉应力为3.35 MPa，而高度1.2、1.4、1.5 m 时拉应力分别降低30.4%、38.7%、38.9%；从拉应力降幅来看，横梁高度增大0.1 m，孔壁最大拉应力平均降低9.1%，但从降幅变化来看，主要集中于高度1～1.3 m 区间内，该区间内孔壁拉应力平均降幅为15.6%，而在高度1.3～1.5 m区间内降幅平均值仅为1%，即随横梁高度增大，虽结构拉应力受抑制，但抑制效应呈逐渐减小态势。与孔壁部位类似，纵梁最大拉应力在高度参数1～1.3、1.3～1.5 m 区间内的平均降幅分别为12.3%、1.6%，表明横梁高度在1～1.3 m 区间内即有显著的张拉抑制效应，且有利于控制结构建造成本。与前两关键部位不同的是，闸门最大拉应力受横梁高度参数影响较小，各设计方案中均稳定在1.7 MPa，最大波动幅度仅为0.6%，且均低于结构安全允许值。从方案优选性考虑，当横梁高度为1.3 m时，闸门、泄流孔壁及纵梁3 个关键部位上最大拉应力分别为2.6、2、1.62 MPa，未超过安全临界值，且加固结构对河口泄流闸孔张拉威胁抑制效果较佳。

2.2 压应力特征

从各计算方案应力结果中提取关键部位上最大压应力，横梁高度参数影响下最大压应力变化特征如图5 所示。从图5 看出，压应力最大部位属孔壁，在高度1.1 m方案中孔壁最大压应力为13.5 MPa，而纵梁、闸门压应力相比前者分别下降21.8%、62.4%。在各设计方案中孔壁压应力与纵梁、闸门部位间的差幅分别达17%～41.5%、1.1～2.33 倍，因而孔壁部位受预压效果最显著。当横梁高度增大后，孔壁、纵梁最大压应力均递增变化，在高度1 m 时纵梁最大压应力为7.6 MPa，而高度1.3、1.5 m 时最大压应力相比1 m 增长了85.3%、91.2%，当横梁高度增大0.1 m纵梁最大压应力平均增幅为14.7%，但在高度参数1～1.3 m 区间内纵梁最大压应力平均增幅达24.2%，而超过1.3 m 后压应力最大增幅仅为2.6%，即预压效果最好方案应在区间1～1.3 m 内。对于孔壁部位来说，在高度1～1.3 、1.3～1.5 m 区间内，其最大压应力的平均增幅分别为16.2%、0.97%，表明孔壁部位预压抗失稳能力变化与纵梁上基本一致，确定横梁高度参数在区间1～1.3 m 更适宜。闸门压应力变化与拉应力变化类似，各设计方案中均稳定在5.1 MPa，表明横梁高度参数改变，对闸门上拉、压应力特征影响较小，而对孔壁、纵梁产生显著影响。从优化方案考虑，横梁高度1.3 m时结构拉、压应力特征俱佳，为最优方案。

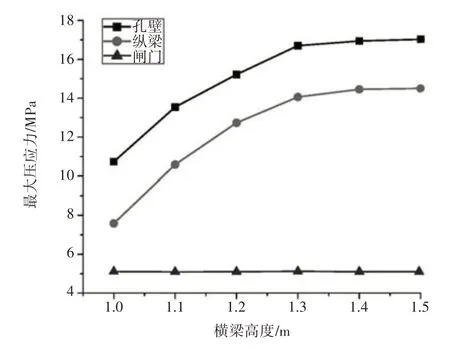
图5 横梁高度影响下最大压应力特征

3 钢结构横梁宽度设计参数优化分析

同理，在不影响结构跨距参数前提下，设定钢结构横梁宽度参数分别为1、1.1、1.2、1.3、1.4、1.5 m，纵梁截面体型保持一致，计算不同方案中关键部位应力特征。

3.1 拉应力特征

不同设计方案计算获得关键部位最大拉应力变化特征，如图6所示。

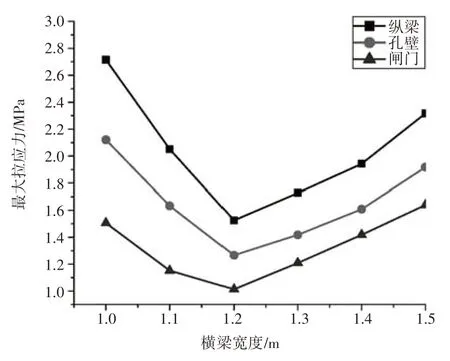
图6 横梁宽度影响下最大拉应力特征

从图6看出，3个关键部位最大拉应力随宽度参数变化趋势基本一致，均呈先减后增变化。以纵梁部位为例，在宽度1 m 时其最大拉应力为2.72 MPa，而宽度增大至1.2 m 拉应力较前者降低了43.8%，而在宽度1.3、1.5 m 时其拉应力较1.2 m 又分别上升了13.3%、51.9%。3 个关键部位拉应力最小均为宽度1.2 m 方案，该方案下闸门、泄流孔壁及纵梁最大拉应力分别为1、1.25、1.52 MPa，满足安全要求。从应力变化特征考虑，当宽度参数在1～1.2 m 区间时，闸门、泄流孔壁及纵梁最大拉应力降幅分别为17.8%、22.7%、25.1%，该区间内宽度参数愈大，对结构张拉作用抑制效果愈佳；而在宽度1.2～1.5 m区间内，3个部位最大拉应力平均增幅分别达17.4%、14.9%、15%，结构张拉作用增强，泄流闸孔受张拉破坏危险性加大。从结构安全性考虑，横梁宽度参数应尽可能不超过1.2 m，以削弱结构拉应力发展趋势；从最优设计方案考虑，当横梁宽度1.2 m时拉应力处于最低，结构抗拉效果最佳，满足结构抗拉特性要求。

3.2 压应力特征

横梁宽度参数影响下关键部位最大压应力变化特征，如图7所示。由曲线变化关系可知，横梁宽度参数与3 个部位最大压应力具有二次函数关系，宽度1.2 m 时各部位压应力最大，闸门、泄流孔壁及纵梁分别为8.3、14.2、11.2 MPa。当宽度参数在1～1.2 m区间时，宽度1.2 m 孔壁最大压应力相比宽度1、1.1 m 分别上升了33.6%、10.4%，3 个部位最大压应力在该区间内平均增幅分别为40.3%、15.7%、19.9%，泄流闸抗失稳倾覆性能逐渐提升，直至宽度1.2 m 时达到最强。当宽度超过1.2 m 后，各关键部位最大压应力均递减，闸门在宽度1.3、1.5 m 时压应力相比1.2 m 分别下降7.3%、51.2%，闸门、孔壁及纵梁在宽度1.2～1.5 m 区间内压应力平均降幅20.7%、12.7%、16.4%。当宽度1.2 m 时，泄流闸孔预压效果最佳，抗失稳滑移性能最稳，而抗拉能力亦最优，为横梁宽度参数最佳方案。

图7 横梁宽度影响下最大压应力特征

4 结论

（1）拉应力最大部位为纵梁，不同高度设计方案其与孔壁、闸门上拉应力差幅分别为13.7%～24.7%、46.5%～1.2 倍；纵梁、孔壁部位最大拉应力随高度参数增大递减，但在高度1.3 m 后降幅减小，两部位在高度1.3～1.5 m 区间降幅仅为1.6%、1%；各设计方案中闸门拉应力均稳定在1.7 MPa。

（2）压应力最大部位为孔壁；孔壁、纵梁最大压应力随高度参数增大递增，高度1～1.3 m 区间内两部位最大压应力平均增幅达16.2%、24.2%，超过1.3 m后增幅较小；随高度参数增大，闸门最大压应力均稳定在5.1 MPa。

（3）关键部位最大拉应力随宽度参数增大呈先减后增变化，拉应力最小均为宽度1.2 m方案，闸门、孔壁及纵梁最大拉应力分别为1、1.25、1.52 MPa；宽度参数与最大压应力具有二次函数关系，宽度1.2 m时各部位压应力最大，宽度1.2～1.5 m 区间内关键部位压应力平均降幅分别为20.7%、12.7%、16.4%。

（4）综合拉、压应力特征，横梁高度1.3 m、宽度1.2 m时为加固结构最优设计方案。