低成本PPP/INS组合导航在车辆导航中的应用

左朝阳，陈 坡,孟东容

(1 西京学院机械工程学院，西安 710123；2 96863部队，河南洛阳 471000)

0 引言

目前，全球导航卫星系统(GNSS)已广泛应用在车辆、航空、农业、测绘等领域中实现定位、导航与授时(PNT)功能，高精度GNSS测量需要用到载波相位测量信息，在差分模式下实现[1]，需要一个基准站和流动站，受到基准站布设成本和无线电通信信道制约。为了消除这种影响，精密单点定位(PPP)应运而生[2]，在PPP模式下，需要从IGS站下载改正参数，使用双频GNSS接收机，可以达到厘米级精度[3]，但是收敛时间较长，且双频GNSS接收机成本较高。

对于车辆等实时性要求较高的用途，分米级或亚米级精度基本上就能满足要求，快速收敛是优先考虑的问题。此外，目前市场上存在大量低廉的单频GNSS接收机，因此，实时SF-PPP成为当前研究的热点[4]。SF-PPP利用单频GNSS观测量和来自国际GNSS IGS观测站的卫星轨道、卫星钟差及电离层垂直延迟的精确改正可以获得较高的精度[5]，但是在城市、峡谷、隧道等车辆经常行驶的路段，这种SF-PPP解决方案将不可用。为了解决在复杂环境下的PPP解决方案中的精度下降问题，与惯性导航系统进行组合，获得连续可靠的导航解决方案。人们对PPP/INS组合导航系统组合模式、系统性能进行了深入研究，但是研究的重点是双频或三频GNSS接收机与战术级的INS组合[6-12]。文中提出一种利用低成本的GNSS接收机和消费级IMU构造实时SF-PPP/INS组合导航系统，来满足车辆定位精度和成本要求。

1 SF-PPP

SF-GNSS接收机在单一频率下提供码和载波相位观测，对于GPSL1码，观测数据可以表示为[13]：

(1)

(2)

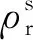
对于SF-PPP所要求的亚米级精度，对流层延迟和相对论效应可以采用经典模型[14]，卫星钟差和轨道误差采用IGS产品来修正。在SF-PPP中考虑码偏、卫星天线相位中心偏移等误差,式(1)、式(2)可以简化为：

(3)

(4)

文中的PPP算法从IGS-RTS中获得卫星轨道和时钟误差、电离层延迟和码偏差的改正。通过扩展Kalman滤波来估计用户三维位置、接收机钟差和浮点模糊度。

INS力学编排的任务是根据IMU的观测量(角速度和比力信息)选取适当的数学模型计算出载体的速度、位置及姿态信息等导航定位参数。相应的数据如图1所示。

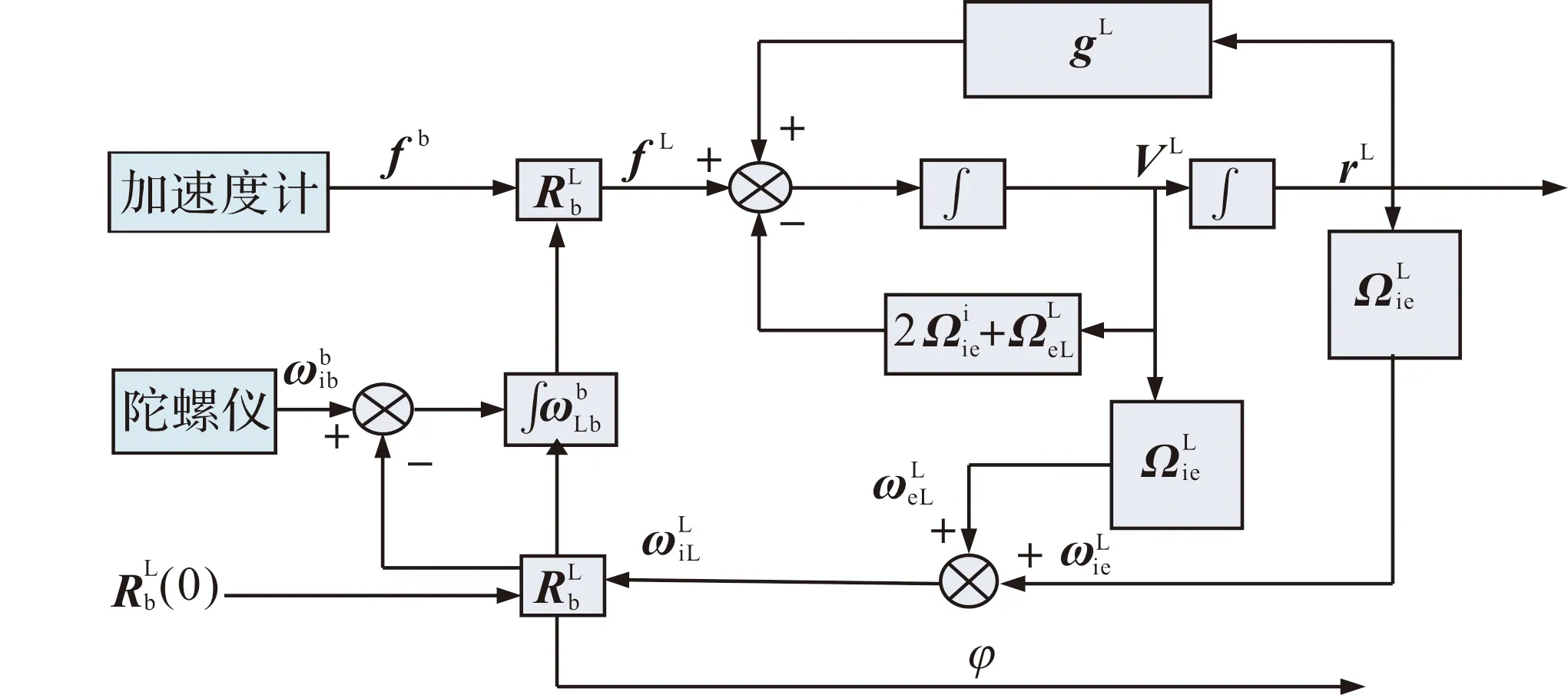
图1 当地水平坐标系下力学编排数据框图

2 INS机械编排

当地水平坐标系下的力学编排方程可以表示为：

(5)

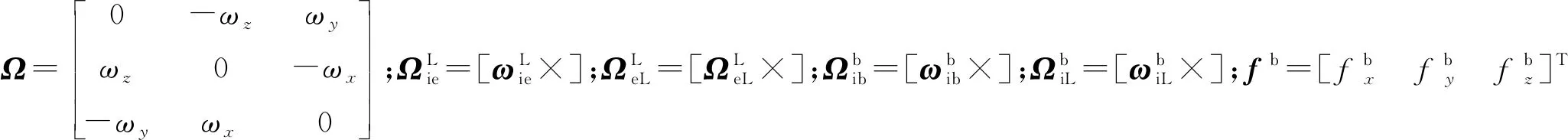
3 PPP/INS组合导航系统

为了充分利用市场现有SF-GNSS接收机，采用松组合模式，直接将SF-GNSS接收机输出信息与INS解算信息进行融合处理。图2给出了所采用的PPP/INS组合导航的框图。

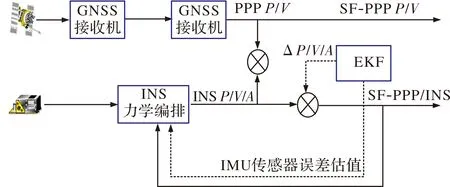
图2 PPP/INS组合导航框图

3.1 状态方程

系统误差模型由15个误差状态组成，可以表示为：

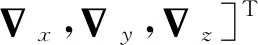
(6)

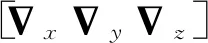
系统模型在连续时间域中可以描述为：

(7)

式中:F为系统动态系数矩阵;W为协方差矩阵Q的过程噪声矢量。动态系数矩阵F的推导见文献[9]。为了获得更好的长期性能，系统模型在F矩阵中考虑了高阶惯导误差项。在EKF的离散实现中，预测基于状态转移矩阵φ，该矩阵可表示为：

φ≈I+FΔt

(8)

式中:I为恒等矩阵;Δt为当前IMU测量值与先前IMU测量值之间的时间间隔。

离散的EKF方程用于预测当前状态及其在k历元处的先验协方差。由于EKF是在闭环结构中实现的，因此每个历元都会重置误差状态，相关过程参考文献[4,15,16]。

3.2 量测方程

线性化的量测模型为：

δZ=HδX+η

(9)

式中:δZ为量测误差矢量;H为量测设计矩阵;η为具有协方差矩阵R的量测高斯白噪声。R的值通过基于统计的PPP解来动态调整。

测量误差矢量表示从惯性导航系统计算出的值与PPP解算出的值之间的差值，可表示为：

(10)

量测矩阵为：

HPPP=[I6×606×9]

(11)

在GNSS信号受遮挡时，PPP不能实现更新，仅采用INS导航解算，尤其是采用低精度MEMS，会导致较大的漂移误差。对于车辆来说，当GNSS信号不可用时，有一些限制因素可以用来辅助惯性导航系统。如零速度更新(ZUPT)和非完整约束(NHC)。在ZUPT中，当检测到车辆处于静止状态时，所有的速度都应该为零[17-18]，这些信息可以用来重置速度误差并限制位置误差的增长。使用ZUPT时，量测误差矢量和量测矩阵表示为：

(12)

HZUPT=[03×3I3×303×9]

(13)

车辆的非完整约束是基于车辆不打滑或飞行的事实，这时仅采用INS导航解算，意味着车辆在横向和向上方向的速度接近于零，因此，NHC的量测更新表示为：

(14)

4 跑车试验及分析

整个系统基于PPI(profound positioning Inc)实时PPP技术采用低成本GNSS接收机来获得可靠的位置信息，基于PPI的实时PPP技术具有快速收敛和GNSS中断后再收敛的优点，这对系统的综合性能至关重要。SF-PPP解决方案同时使用GPS和BDS星座的测量信息。此外，从在线网站可以得到免费的精密卫星轨道、卫星种差和电离层实时校正信息。

INS采用低成本MEMS六轴IMU550。该系统分别在开阔的区域和城市峡谷、立交桥下进行测试。将测试结果与无约束航位推算(UDR)解决方案进行比较，UDR解决方案是目前导航市场上低成本应用的基准,被配置为使用SBAS观测和校正来获得最佳的集成效果。同时在试验车上架设一套含战术级IMU的NovStel SPAN系统，以NovStel配套的IE后处理软件解算值作为理论参考值。设置了两个实验场景。

场景一：在开阔的城市街道，周围遮挡物较少。

场景二：在复杂的城市环境中，经过部分立交桥和隧道区域。

第一次在某市三环路上进行道路测试，持续了大约40 min,表1给出了UDR和文中的PPP/INS解决方案的均方根(σ)和最大误差(emax)。所提出的PPP/INS系统已经达到了亚米级的水平精度，其结果与UDR方案相当。在GNSS系统环境良好的情况下，综合解决方案得益于SF-PPP精确解决方案。

表1 测试场景1中两种方案误差比对

第二次测试是在某市区内进行道路测试，持续了大约1 h，汽车从开阔的天空环境出发，然后穿过几座立交桥和一个比较长的隧道。表2给出了UDR和文中的PPP/INS解决方案的均方根和最大误差。最大误差主要发生在隧道内，而地面导航系统无法解决这一问题。这些结果表明，与UDR方案相比,文中提出的方案精度较好。为了进一步分析，将结果分为两个部分：第一部分为进入隧道之前，第二部分为进入隧道之后。表3显示了第一部分的位置精度比较。结果表明，基于均方根误差的PPP解决方案保持了亚米级精度。在此期间，综合解决方案能够弥补由于立交桥而导致的几次短暂的GNSS信号中断。在这些短暂的中断之后，PPP解决方案能够在几秒钟内收敛到亚米级精度水平，这有助于更稳定和可靠的集成解决方案。图3显示了PPP/INS解决方案在隧道内GNSS信号完全中断时如何优于UDR解决方案。GNSS中断期间的良好性能表明，由于PPP精度和所采用的可靠估计方法，中断前的IMU偏差估计良好。

表2 测试场景2中两种方案误差比对

表3 测试场景2中进入隧道之前两种方案误差比对

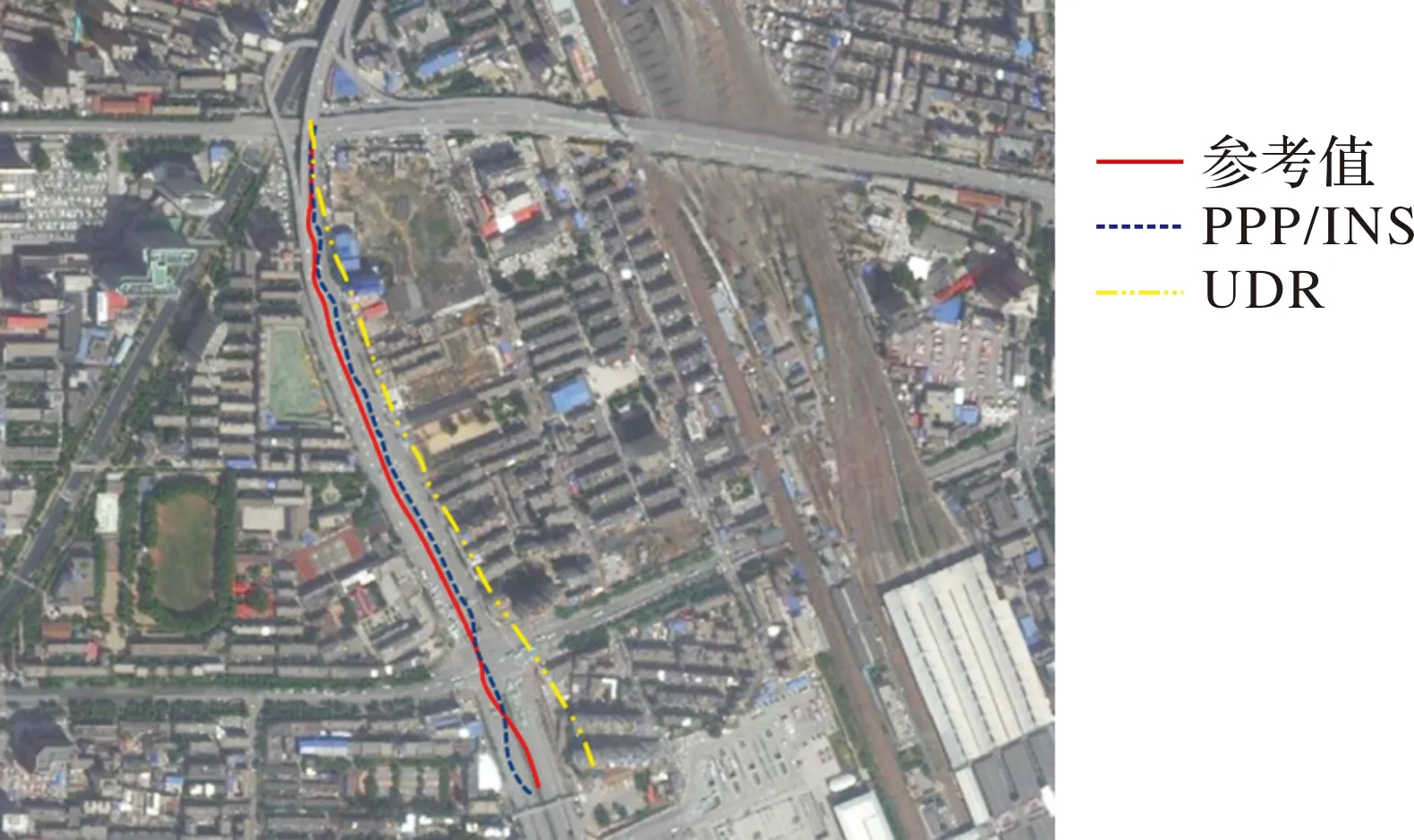
图3 进入隧道后导航结果

5 结论

尽管使用了低成本的IMU和GNSS接收机，但所提出的PPP/INS系统在城市郊区和短暂的GNSS信号中断期间仍能保持亚米级精度。此外，该系统为GNSS复杂环境下的长期导航提供了可靠的解决方案。PPP/INS集成解决方案得益于INS和PPP的高效集成。SF-PPP解决方案有助于在郊区环境中将定位解决方案的精度保持在亚米级。在GNSS信号中断后，实现了快速的收敛。INS解决方案平滑了PPP输出，并用于可靠桥接瞬时和长时间的GNSS中断。所开发的PPP/INS系统有望在车道级车辆导航中发挥重要作用。