模糊聚类-BP神经网络短期光伏发电预测模型

2021-10-27马晓玲张祥飞庞清乐谢青松

物联网技术 2021年10期

马晓玲，张祥飞，庞清乐，谢青松

（1.山东工商学院，山东烟台 264000；2.青岛理工大学，山东青岛 266400）

0 引言

能源行业对工业互联网需求迫切，需要工业互联网提升原有业务系统数据处理和分析能力，实现智能化升级。工业互联网能够为能源行业智能化升级提供关键技术支撑，基于数据驱动的设备预测性维护、工厂能耗优化、企业智能化管理、产业链协同管理、安全环保生产等典型工业互联网应用场景在火电、风电、核电、石化、光伏等行业不断落地。与此同时，传统能源的使用带来的污染问题和储存量迅速减少也引起全球的重视，随着清洁能源的相关技术的发展，发展清洁能源成为各国的共识[1-2]。“十三五”期间，我国光伏产业迅猛发展，但光伏发电受外界因素影响明显，一日之内发电量差异较大，这就导致光伏发电接入电力系统存在不稳定性，不加以解决将会威胁工业设备的安全运行[3]，而准确可靠的光伏预测结果是解决这一问题的重要手段之一[4]。

光伏发电受温度、辐射量、降水量等众多因素影响，现有的传统预测方法准确度不高，在要求精度高的产业无法形成有效参考价值。与传统方法不同，近几年更多的研究人员倾向于先处理样本数据再预测的方法。广义天气类型法[5]是最为常见的传统处理样本数据方法。进行天气类型划分时，利用K均值算法（K-means）[6]可以快速分类，但是参数值难以确定。模糊C均值聚类算法不仅可以优化目标函数，还可以更方便的设置参数，实现按需分类[7]。目前绝大部分研究主要依赖于对光伏场站天气特征信息的收集[8-9]，对时间因素几乎全部忽略。而在电网调度领域每一时刻的发电量越具体，越有利于调度部门作出决策。因此，本文利用模糊C均值聚类算法对数据按时间段进行聚类。

目前常见的预测模型有时间序列法[10]、支持向量机法[11-13]和神经网络法[14]等。其中Elman神经网络计算准确度高、全局稳定性好，但是学习耗时长[15-17]；BP神经网络不仅学习耗时短，而且简单易操作。为了提高预测准确度，本文全面考虑光伏发电量的影响因素，利用模糊聚类（FCM）按照关键特征对样本聚类，最后建立相同特征时段的光伏发电预测模型。算例部分使用澳大利亚艾利斯斯普林太阳能知识产权中心第5号光伏电站的数据做预测，并分别与传统的按天气类型分类的预测结果进行对比。由结果分析得出，本文所提出的预测模型（FCM-BP）每一时刻的准确度更高，这也验证了本文所提出模型的有效性。

1 基于模糊C均值聚类的时间段划分方法

模糊C均值聚类算法在根据特征分类领域应用已经很成熟，其根据数据点和聚类中心的距离，得到每个样本点对所有类中心的隶属度，隶属度越大表明数据点到聚类中心的距离越近。FCM关键在于寻找最小目标函数：

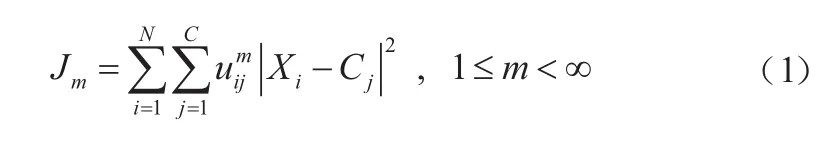
式中：m范围是大于1的实数；uij表示隶属度，即目标函数J中Xi的隶属度；Xi是n维测量数据的第i个数据；Ci是n维的聚类中心；dij=|Xi-Cj|是第i个数据聚类中心与第j个数据点之间的欧几里得距离。

模糊分类是通过对上述目标函数进行有限次的迭代找到的，与此同时，通过式（2）不断更新成员关系隶属度uij和集群中心Ci：

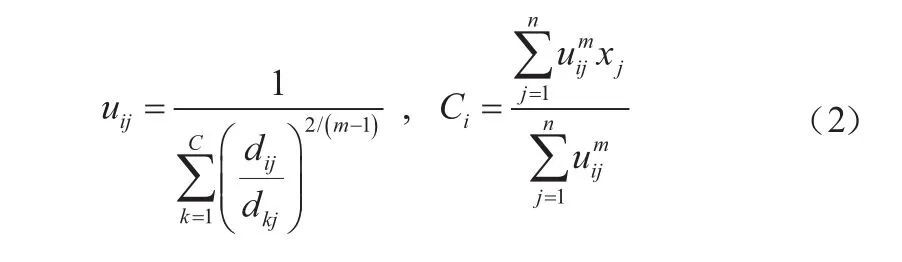
（1）初始化隶属度矩阵U，随机选择[0，1]范围数。

（2）根据式（2）计算聚类中心Ci(i=1, 2, ..., c)。

（3）求解最小目标函数J。根据公式：

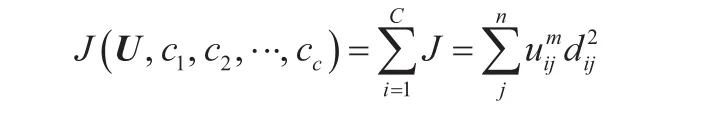
计算目标函数值，当最小值的改变量小于某个阈值时，则停止运算。

（4）根据公式：

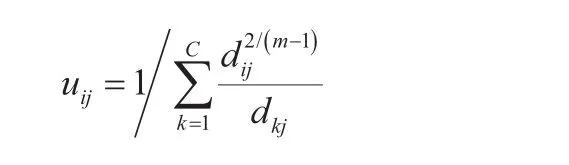
计算更新的隶属度矩阵，返回第（2）步。

2 基于BP神经网络的预测方法

2.1 BP神经网络预测模型

BP神经网络是目前应用最广泛的多层前馈网络之一，一个三层的BP神经网络即可以实现任意精度、近似任意连续函数。BP神经网络的结构主要包括输入层、隐含层和输出层共3层。设神经网络输入层数为m，隐含层数为l，输出层数为n。当一个网络的输入为Xi=(xi,1, xi,2, ..., xi,m)，输出为Yi=(yi,1, yi,2, ..., yi,n)，其中，i为样本类别，网络中激励函数设置f(x)=sgn(x)，则隐含层输出为：

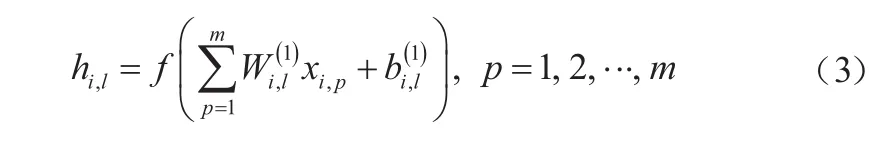
输出层输出为：

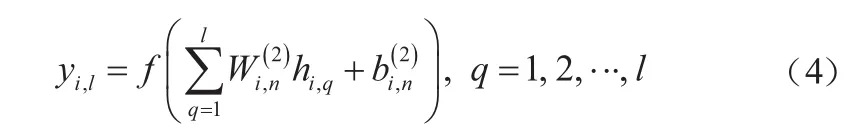
式中：hi,l表示第i个样本的第l个神经元的隐含层输出；f(·)为神经网络隐含层的激励函数；为输入数据样本中第i个样本第l个神经元的输入层与隐含层之间的权值；为输出数据样本第i个样本第n个神经元隐含层与输出层之间的权值；为第i个样本第l个神经元隐含层阈值，为第i个样本第n个神经元的输出层阈值。将输入样本数据从输入层传入，在神经网络中由隐含层传向输出层，如果实际值和期望输出值不存在差异，则二者的误差逐层向输入层反向传递，逐层修正各神经元连接的权值和阈值。

2.2 BP神经网络评价指标

在衡量模型预测的性能时，通常采取下面几个误差指标来衡量：

（1）平均绝对误差率（MAPE）。MAPE 不仅考虑预测值与真实值的误差，同时它主要是显现出误差与真实值的比率。

（2）平均绝对误差（MAE）。MAE是一种基础性的考察误差的指标。

（3）平均平方根误差（RMSE）。RMSE 对异常点比较敏感[18]。

（4）平均方差（MSE）。MSE会通过平方放大偏差较大的误差，主要用来评估出模型稳定性。假定预测值为x={x1, x2, ..., xn}，真实值为y={y1, y2, ..., yn}，4种指标的计算方式为：

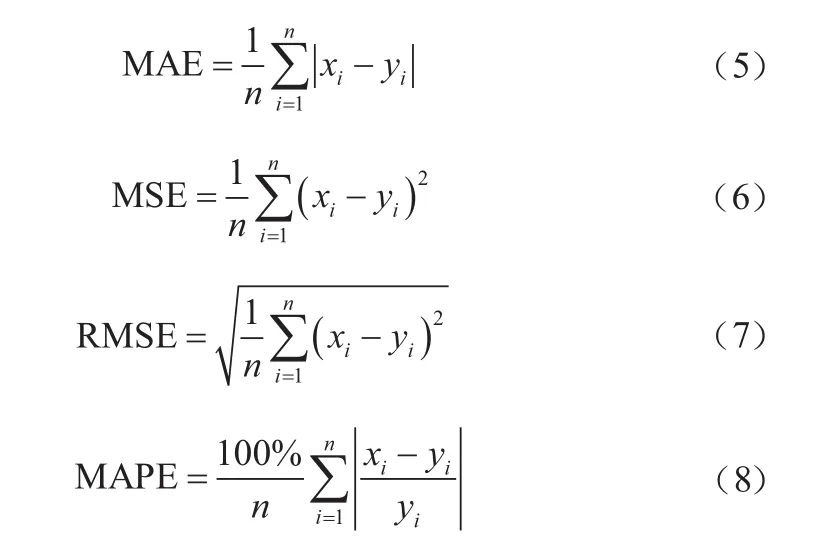
式中：yi为功率实际值；xi为功率预测值；n为数据数量。

3 模糊C均值聚类BP神经网络预测模型

本文使用模糊聚类将样本划分后与BP神经网络相结合建立预测模型。在此，采用模糊C均值聚类对训练样本以及预测日的气象数据进行分类，将数据分为高、中、低三类时间段的数据，即中午时间段对应发电高峰期，上午时间段对应上午发电量逐渐增高的阶段，下午时间段对应下午发电量逐渐下降的阶段，低发电量对应傍晚的低发电量阶段；分别将每一类型的天气特征数据和时间作为BP神经网络的输入进行训练，得到3个模型。

模糊C均值聚类BP神经网络预测模型的详细步骤如下：

（1）考虑时间因素，将时间特征和天气特征同时采用模糊C均值对样本进行分类并分析。

（2）归一化样本数据，包括每一类天气数据和时间数据，神经网络的输入值在（0，1）区间运行比较顺利。

（3）调整神经网络参数，将归一化后的样本数据，即天气数据以及每一个样本对应的时间数据作为输入；调整训练参数，包含学习速率、训练次数和最小误差等，对于输出的结果可以根据误差结果调整神经元个数以达到最优值。

（4）将输出的结果预测值与真实值进行对比，找出误差大的数据进行分析。

4 实验仿真与结果分析

按照时间段类型，分别对早晚时段、上午下午时段以及中午时段进行预测。数据选取艾利斯斯普林斯太阳能知识产权中心第5号光伏发电站2019年1月1日—2020年1月1日的数据，该数据包含每一时刻的温度、风速、总辐射等8组数据，即每天288个采样点。

4.1 数据预处理

4.1.1 数据异常值处理

手动去掉夜间数据，选择每天上午6点到晚上7点的数据，即每天样本数据为165个数据。选取80%的数据为训练样本，选取20%的数据为预测样本。

4.1.2 模糊C均值聚类

将关键特征作为聚类的输入，设定聚类参数。相似日、预测日聚类结果见表3所列。

表3 相似日、预测日聚类结果

4.2 预测结果以及分析

4.2.1 数据归一化

为增加BP网络模型预测的准确性，在将数据应用于BP网络进行训练之前，必须对输入变量和输出变量的的所有样本数据进行归一化处理。本文所有数据归一化后取值为0到1之间，其公式为：

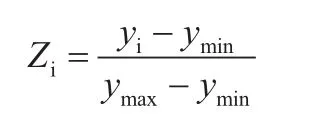
式中：yi为最初数据；ymax，ymin分别为该数据的最大值和最小值；Zi为得到的结果。

4.2.2 模型评价指标

本文采用平均绝对误差（MAE）、平均方差（MSE）和平均绝对误差率（MAPE）三种指标对结果进行评估，其计算公式如式（5）、式（6）、式（8）所示。

4.3 结果分析及对比

由上述分析可知，不同的时间段下发电规律差异明显。对不同的时间段分别进行模型的训练，然后与不分类时的预测结果作对比。晴天各时间段预测结果对比见表4所列，雨天各时间段预测结果对比见表5所列。

表4和表5分别为是9月8号和9月17号的功率预测结果。表4、表5中对模型A进行评价，即表示FCM-BP分时段预测模型；对模型B进行评价，即表示传统按天气分类预测模型。

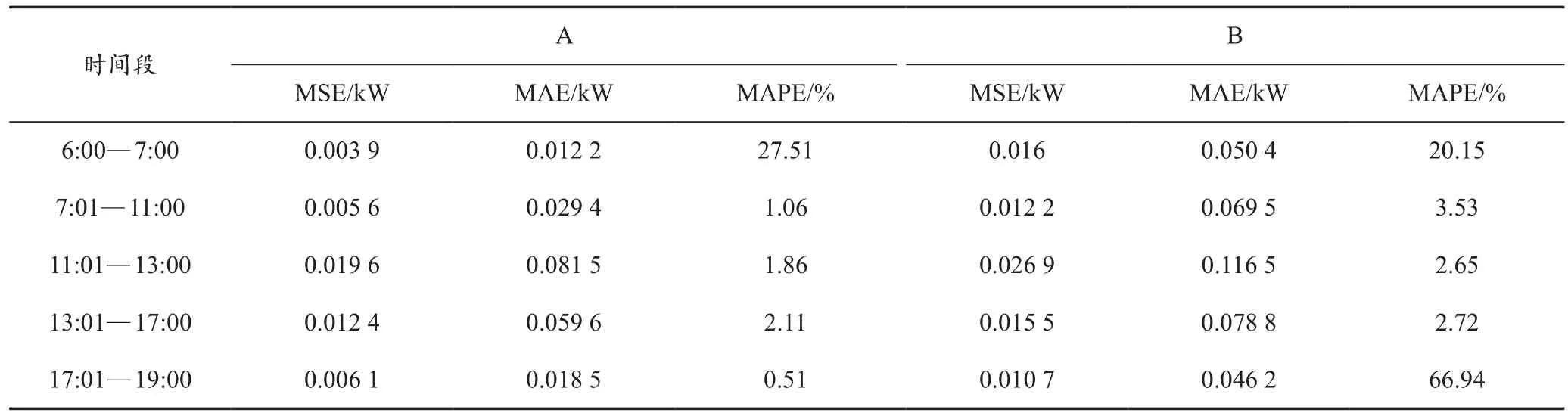
表4 晴天各时间段预测结果对比

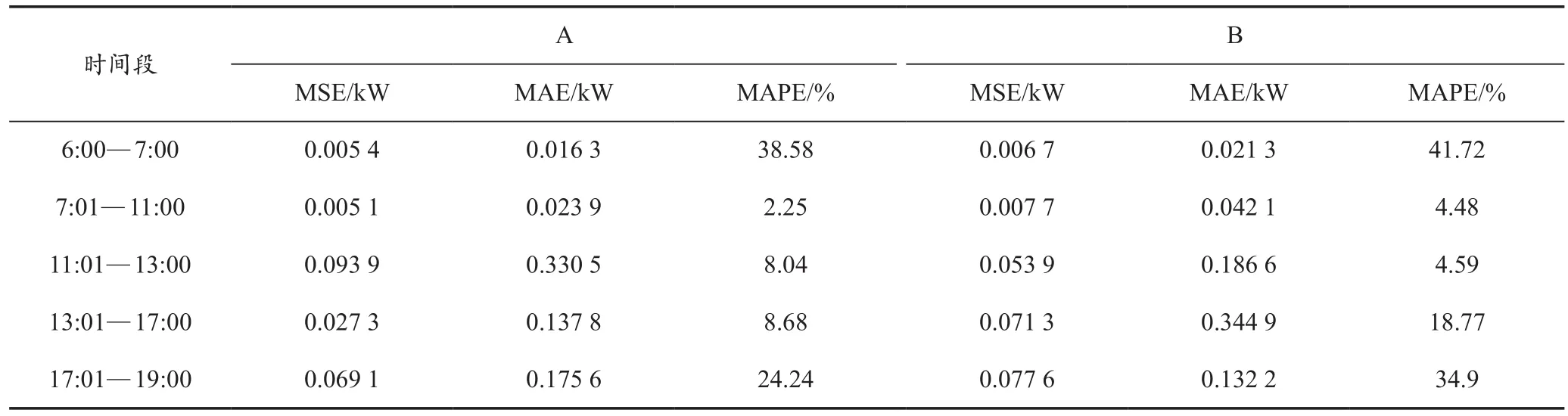
表5 雨天各时间段预测结果对比

由表4可知：晴好天气时，模型A的MAPE均值为6.61%，模型B的为19.20%；模型A的MSE均值为0.010 kW，模型B的为0.020 kW；模型A的MAE均值为0.04 kW，模型B的MAE均值为0.072 kW。晴天在6:00—7:00这个时间段误差较大，这可能是预测日的前一天空气水汽较多影响较大。本文所提方法与传统方法相比，本文所提模型A的预测结果较为准确。

由表5可知：降水天气时，模型A的MAPE均值为16.36%，模型B的为20.89%；模型A的MSE均值为0.040 kW，模型B的为0.043 kW；模型A的MAE均值为0.14 kW，模型B的MAE的均值为0.145 kW。雨天在6:00—7:00和17:01—19:00 这两个时间段误差较大，这可能是仪器受空气中水汽等影响导致数据差异较大。但本文提出的模型的总体预测结果比传统按天气分类预测准确率更高，表明本文提出的模型适应性高，预测精度更好。