基于发电量-负荷平衡的风电系统可靠性预测方法研究

董 锴，蔡新雷，崔艳林，邱丹骅，孟子杰

(广东电网有限责任公司电力调度控制中心,广东 广州 510600)

将风能整合到电力系统中的主要难题之一,是风力输出的随机性及其对电力系统可靠性的影响[1-3],因此国内外各个研究机构和电网运行单位的研究和工作重点,就是风电系统可靠性预测问题[4]。

目前风电系统长期可靠性的预测已经有了一定进展,其中可靠性预测的常用方法,是用有限的历史测量值将模型参数化,然后通过模型生成与数据集相似的合成风数据[5-6],再利用生成的风速数据进行可靠性计算[7-8],这种方法的优点是可以快速生成大量的样本时间序列和相应的概率分布如Elattar E E[9]、Yang L[10]、Zhou J[11]等对威布尔(Weibull)分布的研究,然而从统计模型中获得的合成风数据通常不能用于需要对风速进行积分的情况,这是因为现有模型还没有解决风速与电力需求之间的潜在关联[12]。这可能是因为目前对于风能和电力需求之间的相关性还知之甚少,也很少有测试合成风模型有效性的相关报道,实际上合成风模型有效性至关重要,模型的准确有效可以保证生成的预测数据符合实际工况,从而为可靠性分析提供有用的参考。

因此,从风电系统发电量与负荷平衡关系出发,基于往年的历史风速和电力负荷数据,建立了不同风速分布形式下的风电系统可靠性预测模型。根据不同的风速分布情况提出了对应的可靠性等价条件,通过将预测的发电量和电力负荷与实际值对比,验证模型有效性。最后计算了不同风能波动性、负荷率情况下的风电系统可靠性,讨论了影响可靠性的主要因素。

1 数学模型

从发电量-负荷平衡的角度出发进行可靠性预测,按照以下几个步骤进行:

(1)确定风电系统中的随机变量个数。

(2)针对同一风场的往年风速历史数据进行统计,分析风速的长期概率分布规律。

(3)根据统计数据显示出的概率分布规律,推导计算概率分布参数。

(4)确定发电量-负荷平衡模型中的参数R和L。

(5)计算和评估风电系统可靠性P[R＞L],其中P[·]代表事件发生的概率。

其中风电系统的风速、线损以及用户负荷等变量,可利用折线图、概率图等方法建立其相应的概率分布函数；发电量-负荷平衡模型中的参数R和L,需基于风速、线损、负荷等变量的分布参数,采用模拟方法进行建模。

1.1 发电量-负荷平衡模型

风电系统过去某一年的总发电量用R表示,R值通过风速v和系统损耗loss 的概率模型求得。风速v的概率分布函数按照如下方法求解。

首先根据历史风速数据,采用风速分布中常见的威布尔分布模型,拟合得到风速分布函数,计算分布参数,威布尔分布的累积分布函数如式(1)所示:

式中:各个参数和变量的意义如下:F(v):累积概率分布函数；v:风速变量；f(v):概率密度分布函数；c和k均为Weibull 分布函数的拟合参数。

对式(1)两端同时取两次对数,然后移项整理,就可以将式(1)转换为形如y=ax＋b的线性表达式形式,如式(2)所示:

以式(2)中ln{-ln[1-F(v)]}为输出变量y；ln(v)为输入变量x,可导出Weibull 分布参数的表达式:

式(2)中的函数F(v)可基于历史数据统计模拟得到,如表1 所示是各种不同的参数计算和拟合方法。其中各个参数的意义如下:n:历史数据数目,vx:序列为x的风速实际大小,计算时将所有的历史数据从小到大排列。

表1 F(v)参数计算和模拟方法统计表

通过计算得到分布函数中的参数数值,然后根据分布参数生成随机数u,其取值范围为0≤u≤1；分布方式服从均匀分布,最后经过反变换得到与概率值u相对应的风速样本,反变换公式如式(5)所示:

式中:u服从区间[0,1]上的均匀分布,因此(1-u)也可视为服从区间[0,1]上的均匀分布,则上式可进一步改写为:

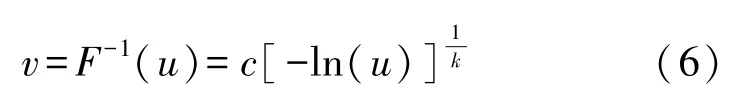
按照上述计算风速v的概率分布函数的步骤,也可以基于风电场损耗loss 的历史统计数据,建立风电场损耗的概率分布模型。基于风电系统损耗和风速的模拟数据,可算得风电场每小时产生的电功率PNet(h):

式中:各个参数和变量的意义如下:NT:风力机数目；Pout:风机的输出功率,实际风力机的输出功率与风场的风速、环境空气参数以及风机自身特性等因素相关；Tloss:通过模型计算得到的总功率损耗。Pout由式(8)计算:

式中:A是风机扫掠面积；ρair是空气密度；Cp是功率系数；v是模拟得到的每小时风速值。总功率损耗Tloss由式(9)计算:

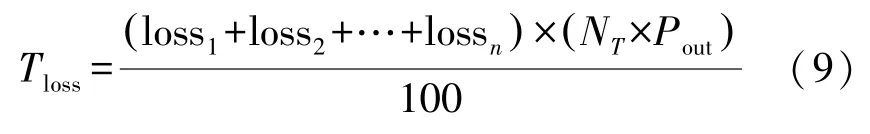
式中:loss1,…,lossn是系统各方面的损耗,包括有风机故障、传输损失、尾流引起的功率损失等,实际工况中风电系统各个部分产生的损耗可以通过实测得到,采用现有的损耗百分比进行建模。风场中所有风机的年发电量R通过如式(10)计算:

由式(10)可以看出,风机年发电量等于一年中各小时发电量的总和,因此根据已有的风力机发电量数据就可以得到总发电量；年发电量R的均值μR和标准差σR由下式(11)、式(12)计算:

现有运行经验表明,风电系统的负荷服从正态分布或对数分布,忽略负荷与风速之间的相关性以简化分析,对风电系统负荷单独建模研究。基于风电场的实际风电负荷数据,拟合风电负荷的分布模型。假设风电负荷为Y,当负荷分布服从对数正态分布时,其均值和方差分别为μ和σ2,进一步可知eY也服从对数正态分布,其均值和方差分别为μ和σ2。

本文采用年度总负荷值表示风电系统负荷L,采用每小时负荷计算值Lh代替PNet(h),通过将Lh代入式(10)即可得到L关于Lh的表达式；通过将L代替R、Lh代替PNet(h)、μR代替μL,再代入式(11)和式(12)即可算得参数L的均值和标准差。

1.2 风电系统可靠性模型

风电系统可靠性即事件R＞L发生的概率,按照式(13)定义:

式中:各个参数和变量的意义如下:fRL(r,l):参数R和L的联合分布函数,按照式(14)计算:

确定fRL(r,l)后,通过对fRL(r,l)进行数值积分即可算得风电系统可靠性指标。通常需要在大量统计数据的基础上,才能建立较为精确的可靠性联合分布函数fRL(r,l)。假设发电量R和负荷L之间相互独立以简化建模过程,通过式(15)建立fRL(r,l)联合概率分布模型:

式中:R和L相互独立,因此fRL(r,l)可以简化为R和L两个变量各自分布函数的乘积,单变量分布函数所需的统计数据较少,因此采用式(15)可有效降低求解难度。将式(15)代入式(13)可得风电系统可靠性计算公式如式(16)所示:

实际运行中发现风机发电量R和系统负荷L可能服从正态分布或者对数正态分布中的一种,此时事件R＞L可按照如下方法进行等价处理:

(1)R和L均服从正态分布时,R＞L等价为R-L＞0。

(2)R和L均服从对数正态分布时,R＞L等价为R/L＞1。

设事件X为R＞L,此时当R和L服从正态分布时,事件X的均值和方差分别按照式(17)、式(18)计算:

根据事件R＞L的等价条件,联立式(17)、式(18)可将系统可靠性指标改写为式(19)所示:

式中:各个参数和变量的意义如下所示:φ(·):标准正态分布变量的累积概率函数。当R和L服从对数正态分布时,事件X的均值和方差可按照式(20)、式(21)进行计算:

联立式(20)、式(21)和对数正态分布条件下的可靠性等价条件,系统可靠性指标按照式(22)计算:

2 仿真计算与分析

通过实测数据进行建模分析,验证模型有效性,首先基于已知的历史数据,模拟风电系统2019 年的发电量和用电负荷数据,再与实测得到的2019 年风电数据对比,分析模型有效性；最后通过计算得到未来一年内风电系统的可靠性,并分析影响系统可靠性的主要因素。

2.1 仿真数据

以某风电场实测历史数据为例进行建模和仿真,风电场共有4 个额定容量为3 MW 的风力机,装机容量为12 MW。采用薛禹胜等[6]的风速统计数据,根据历史数据得到风速与海拔高度的关系如式(23)所示:

式中各个参数和变量的意义如下:v:与海拔高度h对应的风速,风机轮毂的高度取80 m；vref:参考海拔高度href(10 m)处的风速；α为风切角系数0.2。所采用的数据位于2015 至2019 年间,连续5 年内每小时的用电负荷数据,以及2019 年内每小时的风电输出数据。风电系统运行过程中,有多个能量损耗来源,如表2 所示是所采用的风电系统损耗百分比数据。

表2 风电系统中部损耗的比例

建立随机概率分布函数时,风速分布函数基于其月度历史数据,用电负荷分布函数基于其年度历史数据。

2.2 模型有效性

往年风速统计结果显示该风场的风速分布服从威布尔分布,以2019 年8 月的风速为例,采用折线图(图1)和QQ 图(图2)展示统计结果,如图1 和图2所示。

图1 风速历史数据折线图

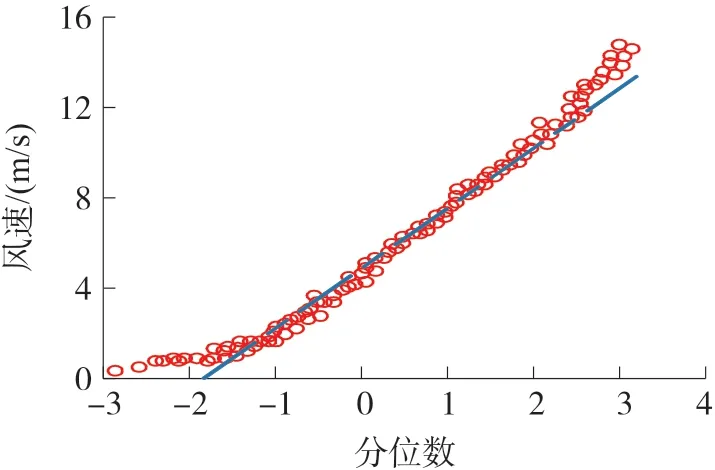
图2 风速威布尔分布QQ 图

由图2 可知风速数据与威布尔分布具有较好的一致性,风速数据散点与威布尔分位数曲线较贴合,表明风速分布服从威布尔分布,因此利用式(3)、式(4)计算分布函数中的参数c和k,参数计算结果的实际值和预测值如图3 所示。

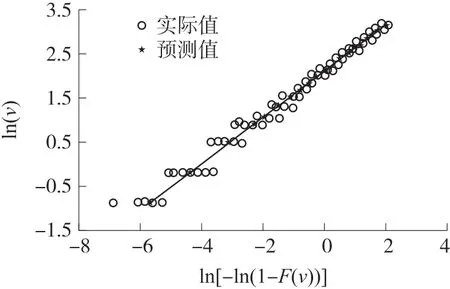
图3 2019 年风速分布参数计算结果

图3 中空心圆圈是实际值,实心五角星是预测值。以2015 至2018 年4 年内每个月的风速统计数据为基础,计算4 年内每个月的风速分布参数,然后再计算分布参数的平均值,用作风速预测的模型分布参数。预测步骤如下所示:

(1) 根据式(6) 风速样本计算公式,通过MATLAB 编写程序生成风速数据。

(2)根据每月风速分布参数结果,计算分布参数c和k的平均值。

(3)根据威布尔分布参数,预测2019 年的每小时风速,最后与实际值对比。

如图3 所示是分布参数的实际值与计算得到的预测值,由图可见所提出的方法有效预测出了2019年的风速分布形式,得到了准确的风速分布参数,证明所预测模型的有效性。在获取风速的概率分布函数和预测值后,采用式(8)计算单个风力机的发电量Pout,采用式(8)计算时的各参数取值为:A=6 300 m2；ρair=1.230 kg/m3；Cp则与风速实际值有关。系统每小时发电量PNet(h)和系统总损耗Tloss分别采用式(7)、式(9)计算,最终采用式(10)计算参数风电系统发电量。

如表3 所示是所预测得到的风电发电量、最大风速值、实际值,以及预测值和实际值之间的相对误差。

表3 2019 年风速、发电量预测结果

同样基于2015 年至2018 年间的风电场负荷历史数据,建立分布函数,计算得到2019 年的负荷预测结果L。负荷的数据以年为单位进行统计,如图4所示是2019 年的负荷变化预测结果统计图。

图4 2019 年负荷折线图

采用与发电量预测相同的步骤,建立负荷的折线图、QQ 图,分析风电场负荷服从的分布规律及分布参数,然后推算风电场负荷的2019 年预测值,最后与实际值比较,结果如表4 所示。

表4 2019 年参数R 和L 预测值和实际值

综合表3 和表4 的结果,可知所提出的方法预测发电量和用电负荷,二者的相对误差均保持在2%以内,表明提出的方法具有有效性。

2.3 可靠性预测结果

通过提出的预测方法,由参数R和L可以计算得到风力发电量和负荷的预测值,基于2015 年至2018 年这4 年的历史数据预测发电量R和用电负荷L参数。在风电系统的负荷和总装机容量保持不变的前提下,通过计算得到每个月的风速分布参数平均值,如表5 所示。

表5 2015～2018 年月风速威布尔分布参数平均值

假设风电系统损耗服从正态分布,基于现有每小时风电系统的发电量,将表2 中的损耗作为均值,设置3 种不同的损耗变异系数(Coefficient of Variation,Cov)5%、15%和25%,采用蒙特卡洛法建立随机性模型对各个损耗进行随机模拟,得到其损耗占比。

由表2 可知风电系统的损耗中loss1 和loss2 占比不超过1%,在模拟过程中可近似认为二者数值不变,通过蒙特卡洛模型计算后,如表6 所示是不同损耗变异系数条件下的损耗、发电量以及风电场最大输出功率。

由表6 可知随着变异系数的增大,损耗的最大值增大、损耗最小值减小、全年总发电量越小,可见变异系数的增大会导致损耗的增加,以及发电量的减少。

表6 不同损耗系数下的风电系统损耗、发电量计算结果

由表7 所示是不同的变异系数下,不同负荷水平(100%、75%以及50%)时得到的可靠性计算结果,参数P[R＞L]表征了在给定条件下(风速、负荷以及系统损耗),风电系统所具有的可靠性,P[R＞L]的数值越系统可靠性越高。

表7 不同变异系数下的可靠性结果

由表7 可知随着负荷水平的降低,系统可靠性增加；负荷水平不变的条件下,系统损耗的变异系数由5%增长至25%时,风电系统可靠性基本上保持不变,表明相比于系统损耗,用电负荷变化对风电系统可靠性的影响更大。

3 结论

针对风电系统可靠性的预测问题,从发电量-负荷平衡角度出发,提出了一种风电系统发电量、用电负荷预测方法。基于风电场的实测数据对提出的预测方法的有效性进行了检验,最后预测计算了风电系统的可靠性,分析了影响系统可靠性的主要因素,得到以下几个主要结论:

(1)对比预测结果与实测结果,显示所提出的预测方法在预测风电发电量和用电负荷时,相对误差均保持在2%以内,表明该方法能够有效预测风电场发电量和用电负荷。

(2)可靠性预测结果显示,随着负荷水平的降低,系统可靠性增加；负荷水平不变的条件下,系统损耗的变异系数增大时,系统可靠性基本不变,表明影响风电系统可靠性主要是负荷水平地变化。