基于改进模糊神经网络的输电线缆制造质量预测方法*
2021-10-26袁少光张卫东耿俊成万迪明
袁少光,张卫东,耿俊成,万迪明,韩 璐
(1.国网河南省电力公司电力科学研究院,河南 郑州 450052;2.国网河南省电力公司,河南 郑州 450000;3.国网信息通信产业集团有限公司,北京 100192)
输电线缆制造质量对于实现电力系统坚强网架结构以及提升电网供电可靠性有着关键的意义[1-2]。传统的输电线缆制造质量通常采用成品检验的方法,无法在线缆形成成品之前及时发现质量问题。同时,传统的输电线缆制造质量评价一般采用人工检测的方式,较大程度上依赖于检验人员的工作经验,无法保障检测可靠性[3-4]。随着工业互联网技术的应用,对输电线缆制造流程中的关键指标进行检测和数据生成已成为可能[5]。因此如何针对输电线缆制造流程中的关键指标对其制造质量进行预测,从而实现对工艺过程的预警已成为一门重要课题。
在质量评价和预测方面的模型主要划分为评价模型和模式识别模型两大类。其中评价模型包括层次分析法[6],模糊聚类评价法[7]等方法;而模式识别包括神经网络[8],支持向量机[9],聚类分析[10],随机森林[11]等方法。为了提升预测的准确性,一般采用模式识别类模型构建相关指标的预测方法。目前已有一些文献将以上模型应用于相关的预测方法中去,比如尹玉娟等[12]基于多核学习支持向量机构建变压器故障诊断预测模型,通过二进制粒子群对支持向量机基核数及模型参数进行了改进。黄青平等[13]将随机森林应用于负荷预测模型中。而神经网络作为一种成熟的预测技术,在较多领域得到了应用,比如叶林等[14]基于模糊神经网络针对分布式光伏的处理进行预测;张义涛[15]采用灰色关联分析结合自适应遗传算法改进的神经网络对配电网线损进行了预测,达到了较优的准确性。高亮等[16]针对太阳辐射量预测问题,采用小波神经网络进行建模。然而目前还很少有文献针对输电线缆制造质量预测问题采用模糊神经网络提出有效的模型,并进行有效的改进。
在输电线缆制造质量预测模型中,部分检测指标的值本身对预测结果的影响不大,而该检测指标的满意程度才是影响预测结果的关键因素。若是采用传统的神经网络进行训练,则该类型指标的具体取值会造成网络的冗余计算,导致网络预测精度的失真。因此采用模糊神经网络将检测指标进行模糊化处理,能够将网络输入数据的关键信息进行提取,有利于训练网络对关键信息的反映,提升预测准确性。在这个过程中,隶属度函数训练过程的学习因子以及后件网络的学习因子直接影响到模糊神经网络的训练误差收敛精度,适合采用合理的算法进行优化。帝国竞争算法(Imperial Competition Algorithm,ICA) 在2007 年 由Atashpaz-Gargari 和Lucas 第一次提出后便在优化领域得到了广泛应用,具备高效的求解效果[17-18]。通过帝国竞争算法对隶属度函数训练过程的学习因子以及后件网络的学习因子进行优化可以有效改善模糊神经网络的性能,从而更加适用于输电线缆制造质量预测中。
本文在基本模糊神经网络的基础上,采用帝国竞争算法对网络中的隶属度函数和后件网络学习因子进行优化,从而对模糊神经网络的训练性能进行改进。基于帝国竞争算法优化模糊神经网络对输电线缆训练样本进行训练,训练完成后对检验样本进行检验,得到输电线缆各批次合格率与实际检验合格率的对比,验证了所提出方法的有效性。
1 模糊神经网络原理
模糊神经网络相比于传统的神经网络,在输入层“隐含层”的基础上还增加了模糊化层以及模糊规则计算层。模糊神经网络的网络结构相比于传统的神经网络层数更多。在模糊神经网络的训练过程中,一方面需要对隐含层和输出层的节点权重和阈值进行训练,另一方面也需要对模糊化层的隶属度函数进行训练。
对于m层神经网络,假设输入层样本为X;第k层的i神经元输入,输出;k-1 层神经元j到k层神经元i的权系数为Wij;激发函数为f,i神经元的阀值为θi。神经网络隐含层以及输出层的权系数和阈值采用正向和反向传播进行训练[19-20]。而模糊神经网络的模糊化层隶属度函数采用高斯函数如式(1)所示。

式中:μ(xi)为第i个模糊子集的模糊神经网路的隶属函数;xi为第i个模糊子集的函数输入变量;为第i个模糊子集第j个输入参数的隶属函数的均值;为第i个模糊子集第j个输入参数隶属函数的宽度;n为模糊子集数目;k为输入参数的数目;
若当前神经网络训练到t代,则需要通过神经网络训练过程对后件网络的权重以及模糊化层中隶属函数进行训练,主要体现为对高斯函数的均值和宽度进行训练,具体过程如下:
(1)对神经网络期望输出值和实际输出值之间的误差如式(2)所示。

式中:e为期望输出值和实际输出值的误差;yd为期望输出值;yc为实际输出值。
(2)对后件网络的权重进行修正,修正过程如式(3)所示。
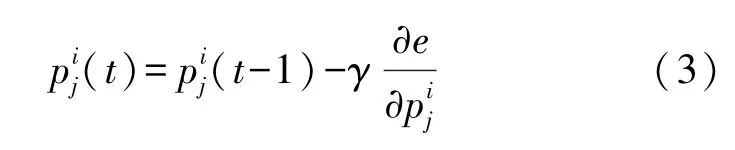
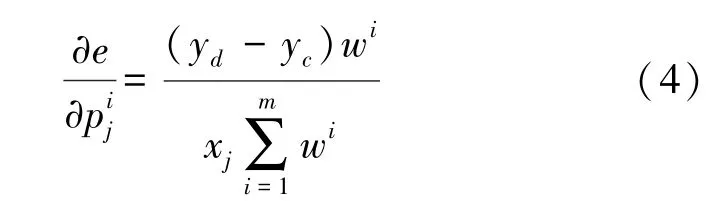
(3)对模糊化层的隶属度函数进行训练,更新高斯函数的均值和宽度分别如式(5)和式(6)所示。
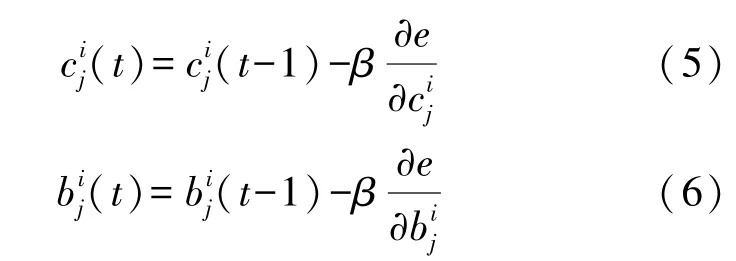
尽管目前对模糊神经网络的研究比较成熟,然而对于网络中的模糊化层隶属度函数的学习因子β和后件网络权重的学习因子γ一般只能采用运行经验进行确定,这对于构建最优的模糊神经网络较为不利,有必要采用优化算法对其进行寻优。
2 帝国竞争算法与学习因子优化
采用帝国竞争算法对学习因子β和γ基于输电线缆制造质量的历史数据进行优化,得到较优的模糊神经网络。基于帝国竞争算法的模糊神经网络学习因子β和γ优化流程如下:
(1)国家种群的初始化。以学习因子β和γ作为国家位置随机生成N个国家。
(2)针对任意一个国家i,以β(i)和γ(i)作为模糊神经网络隶属度函数的学习因子β和后件网络权重的学习因子γ,对神经网络进行训练得到误差收敛值。
(3)根据每个国家目标函数与最大值的偏离情况构建国家相对势力,即以如式(7)所示的方式计算第i个国家的相对势力。

式中:Fi[β(i),γ(i)]为第i个国家相对势力;fi[β(i),γ(i)]为第i个国家目标函数;J为国家集合。
把其中势力最强的Nimp个国家看作是帝国,剩余的Ncol个国家看作殖民地。
(4)殖民地分配。基于式(8)对殖民地在帝国之间的分配数量进行制定。殖民地依据该数量在帝国之间进行随机分配。

式中:round()为地板函数。Nj为第j个帝国的殖民地数量;Fj为第j个帝国相对势力。
(5)帝国对殖民地的同化过程。令每个帝国所属的殖民地以式(9)的方式进行同化过程。

式中:xn,i(k+1)和xn,i(k)分别为第n个国家第i维位置变量在k+1 次迭代和k次迭代值;ximp,i(k)为该国家所属帝国k次迭代第i维位置变量;rand 为区间[0,1]的均匀分布随机数;d为殖民地同化距离系数;δ为殖民地变革距离系数。
(6)帝国与殖民地交换身份
假如有殖民地的势力大于该殖民地所属的帝国势力,则交换该殖民地与帝国的身份。
(7)帝国对殖民地的竞争。定义帝国集团n的势力为En,竞争过程如式(10)所示,其中En如式(11)所示。
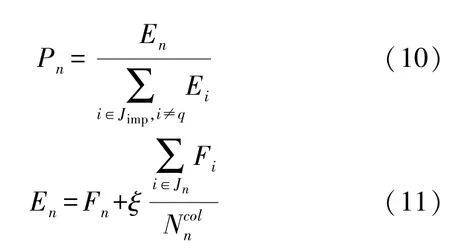
式中:Pn为殖民地被帝国n瓜分的概率;ξ为殖民地势力构成系数;Jn为帝国n的殖民地集合;Fi为殖民地i的势力。
(8)帝国消亡。某个帝国失去了所有殖民地时,那么其就发生消亡。若当前还存在多个帝国,则返回步骤(3),否则输出唯一帝国的位置β和γ作为模糊神经网络的学习因子。
3 输电线缆制造质量预测流程
(1)针对输电线缆制造工艺流程,选取包括拉丝线速度、导体绞制线速度、导体成缆长度、绝缘平均厚度、除气室温度、护套牵引速度以及皱纹护套焊接电流在内的7 个关键指标作为模糊神经网络的输入层指标。以输电线缆检测合格率作为神经网络输出层指标。
(2)初始化模糊神经网络,包括隐含层以及输出层的权系数和阈值以及隶属度函数的学习因子β和后件网络权重的学习因子γ,对每个输入层指标初始化模糊隶属度函数均值和宽度。
(3)将输电线缆制造数据划分为训练样本和检验样本。采用帝国竞争算法对2 个学习因子β和γ进行寻优,寻优过程中调用神经网络训练流程。
(4)以优化得到的β和γ对模糊神经网络进行训练,对网络结构和参数进行更新。
(5)判断神经网络训练次数是否达到了最大迭代次数,如果是则算法结束,输出网络,否则判断误差是否收敛,如果收敛则输出网络,否则返回步骤(4)。
综上所述,基于帝国竞争算法改进模糊神经网络的输电线缆制造质量预测流程如图1 所示。

图1 基于帝国竞争算法改进模糊神经网络的输电线缆制造质量预测流程
4 仿真算例
针对某地区输电线缆制造项目采用自动化的工艺流程检测技术,得到输电线缆制造质量历史运行数据176 组,每一组数据代表一个批次的输电线缆,每组数据包括该批次输电线缆的工艺流程指标即拉丝线速度、导体绞制线速度、导体成缆长度、绝缘平均厚度、除气室温度、护套牵引速度、皱纹护套焊接电流以及该批次输电线缆的检验合格率。将其中100 组数据作为样本数据对模糊神经网络进行训练,将剩下的76 组数据作为检验样本对训练完成的模糊神经网络进行检验。对模糊神经网络进行初始化,其中输入层节点有7 个,输出层节点有1 个,7个输入层数据的模糊分割数均为3,因此模糊化层的节点数为21 个。
首先基于帝国竞争算法对学习因子进行寻优,得到2 个学习因子与帝国竞争算法迭代次数的收敛曲线以及相应的神经网络最小收敛误差和迭代次数的关系分别如图2 和图3 所示。

图2 模糊化层隶属度函数的学习因子和后件网络权重学习因子与帝国竞争算法迭代次数的收敛曲线

图3 神经网络收敛误差和帝国竞争算法迭代次数的关系
从图2 和图3 中可以看出,通过帝国竞争算法的优化求解,模糊化层隶属度函数的学习因子最终在386 代收敛到了0.027,同时后件网络权重学习因子在537 代收敛到了0.086。在2 个学习因子发生收敛的同时,随着学习因子的寻优,模糊神经网络能够达到的最小收敛误差随着算法迭代收敛到了5.321 2×10-5。
基于寻优得到的学习因子,再一次对模糊神经网络进行训练得到7 个指标的隶属度函数均值和宽度如表1 所示。

表1 输电线缆制造质量相关指标的隶属度函数均值和隶属度函数宽度
从表1 中可以看出,通过训练得到的隶属度函数均值基本上与以上指标的理想值接近,而隶属度函数宽度的大小则决定了该指标与隶属度函数均值偏差导致的满意度指标下降速度。在所有输电线缆制造质量预测模型的输入指标中,线缆质量对于拉丝线速度,绝缘平均厚度以及护套牵引速度的精度要求较高,因此其隶属度函数宽度相比于隶属度函数均值的比例较低;而线缆质量对于导体绞制线速度,导体成缆长度,除气室温度以及皱纹护套焊接电流的精度要求较低,因此其隶属度函数宽度相比于隶属度函数均值的比例较高,训练结果与工程实际相吻合。
同时可以得到模糊神经网络在训练过程中的误差收敛曲线如图4 所示。图中纵坐标采用对数形式描述模糊神经网络的训练误差。

图4 模糊神经网络训练误差和训练代数的关系
从图4 中可以看出,随着迭代次数的增加,模糊神经网络的训练误差不断向期望训练误差收敛。事实上经过15 代的训练,模糊神经网络的训练误差收敛到了5.321 2×10-5,达到了期望的收敛误差精度3.6×10-4。
基于构建和训练完成的模糊神经网络,针对检验样本中的输电线缆批次进行制造质量预测,可以得到76 组检验样本的制造质量预测合格率和实际检测合格率的对比如图5 所示,而每一批次输电线缆的预测合格率和实际检测合格率偏差如图6 所示。
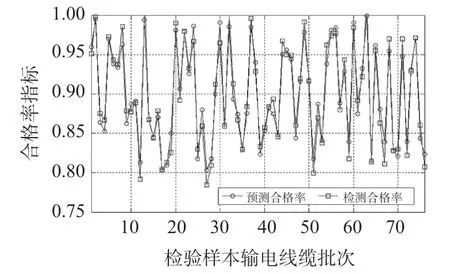
图5 检验样本的输电线缆批次制造质量预测合格率和实际检测合格率对比
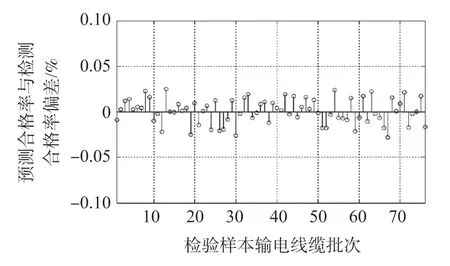
图6 检验样本的输电线缆批次制造质量预测合格率和实际检测合格率偏差
从图5 和图6 中可以看出,基于模糊神经网络的对检验样本输电线缆批次制造质量合格率预测与实际检验合格率较为接近,平均绝对预测误差为0.007 62%,能够实现在生产工艺阶段对输电线缆的制造质量进行较为准确的预测,从而对输电线缆生产线作出及时的预警。
为了对比模糊神经网络相比于传统的BP 神经网络以及自组织映射神经网络,也为了检验引入帝国竞争算法对模糊神经网络学习因子优化的效果,针对同样的训练样本进行网络训练,并采用同样的检验样本采用4 种方式对输电线缆制造质量合格率进行预测得到预测合格率和实际检测合格率平均绝对偏差如表2 所示。其中方式1 为基于BP 神经网络,方式2 采用自组织映射神经网络,方式3 采用基本模糊神经网络,方式4 为基于改进模糊神经网络。

表2 4 种方式下神经网络对输电线缆制造质量合格率预测平均绝对偏差对比
从表2 中可以看出,基本模糊神经网络相比于传统的BP 神经网络和自组织映射神经网络,其预测平均绝对偏差显著更低;同时在基本模糊神经网络的基础上采用帝国竞争算法对学习因子进行优化可以进一步改进模糊神经网络的预测效果,降低预测平均绝对偏差。
5 结论
(1)提出基于帝国竞争算法改进模糊神经网络的输电线缆制造质量预测模型,为构建输电线缆制造质量生产流程预警机制提供坚实的基础。
(2)仿真算例表明,相比于传统的神经网络以及基本模糊神经网络,改进模糊神经网络在输电线缆制造质量合格率预测中,其预测平均绝对偏差显著降低,验证了模型的有效性。
