基于改进型HHT的转子断条故障诊断方法的研究
2021-10-26杨海军查学刚赵玉桂周保军包继华
杨海军,查学刚,赵玉桂,周保军,包继华
(1.国家能源集团 宁夏煤业有限责任公司信息技术中心,银川 750001;2.山东科技大学 机电学院,山东 青岛 266590;3.山东科大机电科技股份有限公司,山东 济宁 272000)
0 引言
异步电动机在工业上具有举足轻重的地位,其运行的可靠性和稳定性对于提高经济效益、保障操作人员安全具有重要意义[1-4]。众所周知,异步电动机在出现转子断条故障时,在电源频率两侧出现(1±2s)f1故障边频分量[5-6]。由于异步电动机转差率较小,边频分量容易被基波频率淹没。为此,本文提出采用四阶巴特沃斯带阻滤波器,将阻带带宽设置在1 Hz以内,以供电频率为阻带中心频率。目的是为了将供电频率滤除或削弱,从而有效凸显故障边频分量。
1 经验模态分解原理
经验模态分解(EMD)是由黄锷博士等[7-10]提出的一种具有自适应能力的算法,对于解决非线性、不平稳的信号具有良好的作用[11-12]。EMD算法假设任何一个信号都可以被分解为若干个本征模态函数(IMF)和一个残余分量。IMF分量满足2个条件[13]:1)整个数据段内,极值点的个数和过零点的个数相等或最多相差不超过1个;2)在任意时刻,由局部极大值构成的上包络线和局部极小值构成的下包络线的平均值关于时间轴对称。
通过以上2个条件的限制保证了EMD分解对时间序列提取出的瞬时频率具有实际意义。EMD分解的过程如下:

信号不可能无限次地分解下去,当其不收敛时,采用x(t)分解前后结果的标准差作为停止准则来控制分解的次数,即

根据前人研究的成果可知,SD的取值一般在0.2~0.3时分解效果是最佳的。
2 希尔伯特谱分析

3 EMD算法的改进
3.1 滤波器设计
受工业现场强噪声、强干扰影响,采集的信号被严重污染。基于HHT算法对原始信号处理时,效果并没有那么理想,存在频率混叠现象。为此,本文基于LabVIEW设计了一个巴特沃斯滤波器对原始信号预处理,将处理后的信号再进行HHT[14]。
巴特沃斯滤波器具有单调下降的幅频特性,而且相位也具有良好的线性度。一般以巴特沃斯低通滤波器的设计为基础,其他类型的滤波器基于频率变换相互转换。
构造一个仿真信号x(t)模拟转子断条故障,加入幅值为0.8的高斯白噪声信号,3个频率分别为45、50、55 Hz的正弦信号叠加如式(9)所示,该仿真信号的原始波形和采用4阶巴特沃斯低通滤波器滤波后的信号如图1所示。
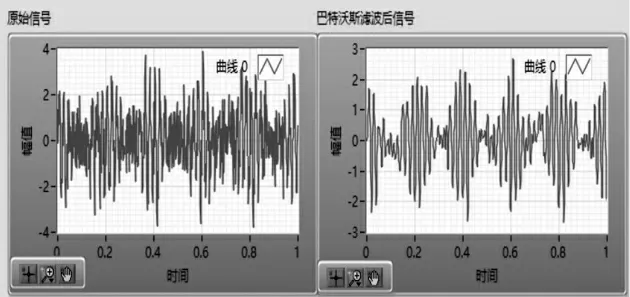
图1 仿真信号原始信号和滤波后时域波形图
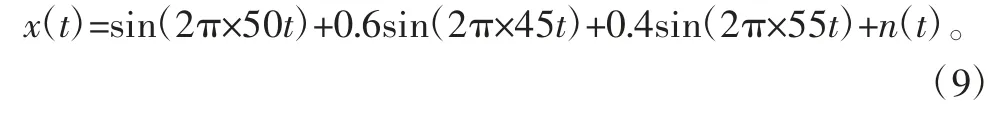
如图2所示,基于巴特沃斯带阻滤波前后的FFT频谱图,通过比较看出设计的滤波器效果较好,对阻带频率成分削弱或抑制作用突出。为了凸显故障分量,低通滤波器转换为带阻滤波器,将基频50 Hz滤除,只保留(1±2s)f1边频分量,排除基频的干扰。因此,设置阻带低截止频率为49.5 Hz,高截止频率为50.5 Hz,阻带带宽仅为1 Hz。首先采用低通滤波器排除高斯白噪声的干扰,然后采用带阻滤波器滤除基频的干扰,对滤波前后的信号分别做FFT,对比可知通过滤波后的仿真信号更能凸显故障特征频率。

图2 仿真信号滤波前后的FFT频谱图
3.2 虚假分量问题
采用EMD算法对信号进行分解时,会产生一些多余的IMF分量,这些分量被称为虚假分量。虽然有一些IMF分量是可以通过主观分析来判断出来,但有一些是肉眼看不出来的,因此针对虚假分量应采用理论算法分析判断IMF分量的真实性。
继续对公式(9)的仿真信号x(t)进行EMD分解,结果如图3所示,从图中可以直观地看到IMF7可能是虚假分量。该仿真信号包含3个频率分量和1个高斯噪声信号,通过EMD分解却得到了7个模态分量和1个残余分量,显然其中具有无意义的虚假分量。
图3 仿真信号的EMD分解
3.3 改进EMD算法
针对EMD分解的虚假IMF分量问题,本文提出了一种基于互相关分析的改进EMD分解算法。对EMD算法分解出的每一个IMF分量与原始信号做相关分析,二者之间互相关系数的大小直接反映了原始信号中是否含有该IMF分量。
相互相关不仅能够反映信号的幅值,而且能够反映信号的相位信息。本文为判别IMF分量的真实性,取IMF分量和原始信号做相关分析。因此,基于互相关更具优势。
信号x1(t)和y1(t)本身值的大小会影响二者互相关的结果。因此在比较不同的随机信号之间的相关性时,仅仅视其相关函数值的大小是不准确的。例如一对大信号,虽然相关程度很低,但是相关函数的值却很大;反之,虽然相关程度很高,但是相关函数值却很小。为了避免信号本身数值的影响,需要将信号做归一化处理。

由互相关的性质可知,对于EMD分解出的IMF分量若是真的分量,则IMF分量与原始信号的互相关函数应大于0;反之,虚假分量与原始信号的互相关函数应趋于0。根据以上分析,对公式(9)中仿真信号EMD分解的每一个IMF分量与x(t)做互相关,其结果如图4所示。
基于相关分析对2个信号处理时,若2个信号含有相同的谐波分量,则在互相关之后特征频率处的幅值增强,反之,则幅值减弱。从图4可以看到,基于EMD分解将仿真信号x(t)分解出的频率依次递减的IMF分量分别与x(t)做互相关的结果。IMF1分量与原始信号的互相关在时域上结果趋于0,第一个分量就是信号中掺杂的高频白噪声信号。IMF5~IMF7分量与原始信号的互相关幅值趋近0,因此,这些IMF分量都是虚假分量。IMF2~IMF4分量与原始信号的互相关的结果是周期性的随机信号,因此可以判定这2个分量是真的模态分量。

图4 仿真信号与IMF的互相关
4 实验验证
4.1 实验系统概述
设计的实验系统如图5 所示。电动机型号为YXL80M2-4,额定电流为1.9 A、额定功率为0.75 kW。

图5 故障检测实验平台实物图
4.2 转子断条实验分析
采用加工了断条故障的异步电动机进行实验。如图6所示,在笼型转子上切割了一条缝隙来模拟转子断条的故障特征。断条电动机供电频率分别为40、45、50 Hz,负载分别调节为轻载、半载和满载,观察电流频谱的变化情况。在该实验中,采集A、B、C三相定子电流信号,基于FFT和改进的HHT分析电流信号的频谱特征。

图6 内置转子断条电动机实物图
如图7所示,文中列出了供电频率为50 Hz、半载时的三相电流的时域信号。从时域信号中可以看到三相电流不是标准的正弦信号,电流有一定的波动,存在毛刺。
图7 50 Hz、半载、故障电动机三相电流时域信号
其他几组实验过程仅以表格的形式呈现数据,如表1~表3所示。
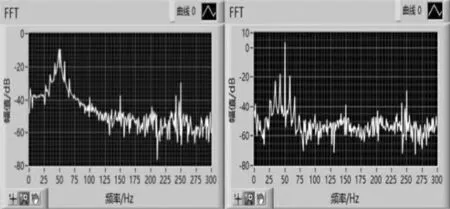
图8 50 Hz、半载、带阻滤波前后FFT
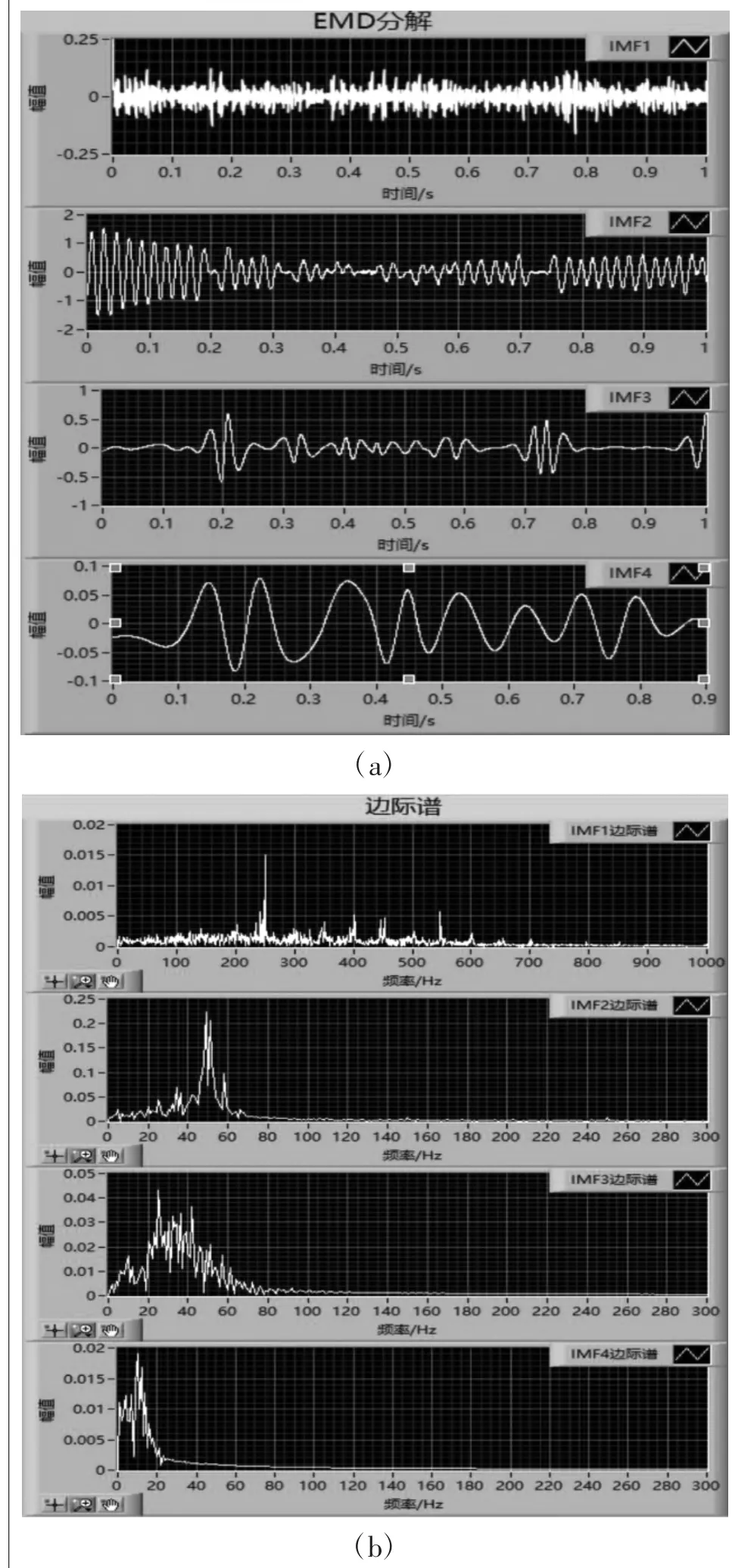
图9 50 Hz、半载、带阻滤波后故障电动机HHT
从表1~表3中数据可知,供电频率一定的情况下,分别调节负载的大小可以发现随着负载的增加,(1±2s)f1故障频率分量的幅值也在增加[15];电动机在轻载和半载时电流较小,边频分量也更难看出。实验中异步电动机的额定转差率为0.05,即故障边频分量与基频分量相差5 Hz。实际故障电动机在运行时中,转速略低于额定转速。当电源频率一定时,异步电动机的转速有30 r/min左右的波动。因此,故障边频与基频差值略微增大,通过巴特沃斯带阻滤波后,然后进行HHT算法分析,也更能突出故障分量。
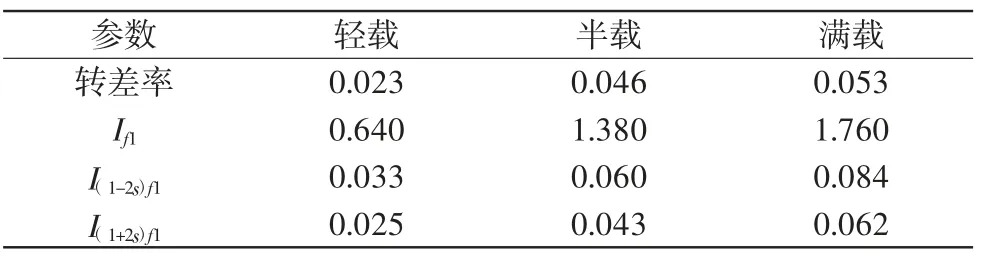
表1 供电频率40 Hz时电动机运行参数

表2 供电频率45 Hz时电动机运行参数
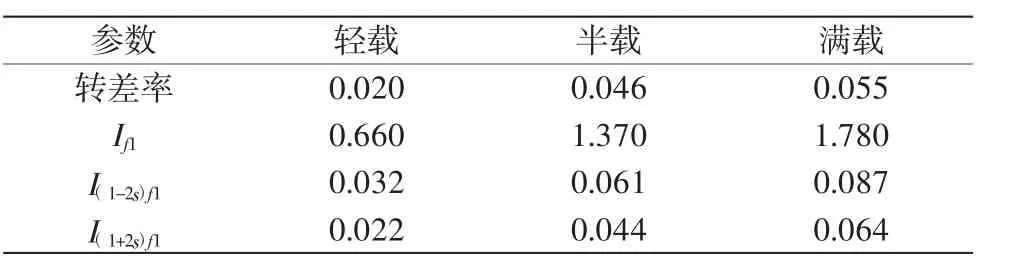
表3 供电频率50 Hz时电动机运行参数
5 结论
1)提出基于四阶巴特沃斯带阻滤波器对定子电流信号滤波的方法。将阻带宽度设置在1 Hz以内,以电源频率为阻带中心频率,滤除基波分量,有效突出了故障边频分量。仿真和实验证明该方法可以有效识别转子断条故障特征。
2)提出巴特沃斯滤波和相关分析相结合的改进的HHT算法。对信号滤波后再进行EMD分解,可以有效解决模态混叠问题;将IMF分量与滤波后的信号做相关分析可以准确识别虚假分量。仿真和实验证明了该方法的可行性。
3)改变供电频率和负载大小,通过巴特沃斯带阻滤波器对电源频率削弱或抑制可以有效凸显边频分量2sf1,转子断条时定子电流略有降低,转速有30 r/min左右的波动。
