某型榴弹弹体内膛加工折弯刀杆设计

2021-10-26郑利民李艳飞

机械制造与自动化 2021年5期

郑利民，李艳飞

(辽沈工业集团有限公司，辽宁沈阳 110045)

0 引言

榴弹是弹丸内装有猛炸药，主要利用爆炸时产生的破片和炸药爆炸的能量以形成杀伤和爆破作用的弹药总称[1]。这种弹药威力的发挥主要是依靠榴弹的战斗部，其战斗部主要由炸药装药和弹体两部分组成，而在榴弹的生产过程中，在弹体加工完成后才能将炸药装入弹体的内膛。因此弹体的内膛加工质量制约着炸药的装药量，从而影响榴弹战斗部威力的发挥。所以榴弹的内膛加工就成为了弹体加工的重要工序。

榴弹弹体的内膛一般包括弹体内表面的圆柱部和弧形部。弧形部在弹体的收口工序及旋压等过程中已经形成，故在机加工艺中不安排内表面加工工序[2]，所以在机加过程中只需完成对内膛圆柱部的加工。本文针对某型榴弹在进行弹体内膛圆柱部加工时尺寸加工不到位的问题，通过对刀杆和弹体口部尺寸的分析，提出在原有刀杆的基础上进行折弯设计，从而实现对某型榴弹内膛圆柱部的高质量加工。

1 折弯力计算及仿真分析

1.1 刀杆折弯力的确定

图1所示为某型榴弹与内膛车刀加工内膛时的相对位置示意图。从图中可以看出，弹体内膛圆柱部距离弹体内膛口部底部距离为87.5mm，当刀杆伸入内膛口部达到该距离后，刀尖与加工内膛圆柱部的端面距离相差约6.67mm，因此要想完成对某型榴弹内膛圆柱部的加工，需要使刀杆向下弯曲6.67mm，这样才能使刀杆接近口部边缘后也能够使刀片完成对内膛圆柱部的加工。

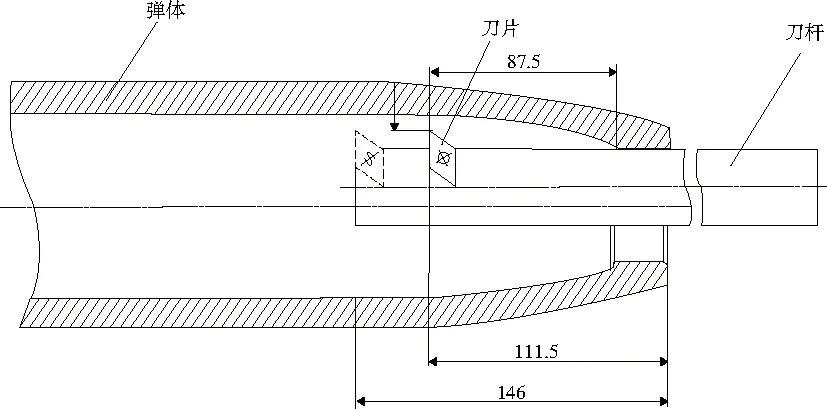
图1 某型榴弹内膛加工示意图

通过上面的分析，将刀杆折弯的受力状态简化为如图2所示的力学模型。图2中A点对应图1中刀杆伸入榴弹内膛时与口部底面的接触位置。B点为刀杆头部位置。因此AB两点的距离l为87.5mm，最大挠度WB为6.67mm，所以根据最大挠度[3]计算公式

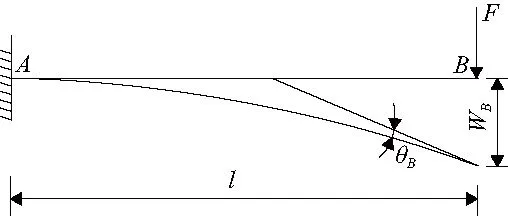
图2 刀杆受力折弯力学简图

(1)

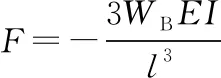
(2)

式中的截面惯性矩I与刀杆的截面形状有关，刀杆的截面形状尺寸如图3所示为非规则截面，所以需要借助CAD软件进行计算，经计算，结果为Iy=49 605.850 8mm4，Ix=47 879.843 8mm4。所以计算时取I=Ix；刀杆材料为42CrMo，根据文献[4]弹性模量为E=2.12×1011Pa。将所有已知数据带入式(2)，可得折弯力为303 187.656N。

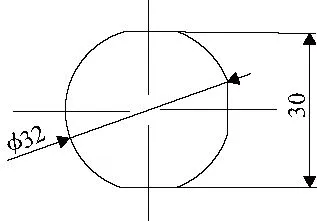
图3 刀杆截面图

1.2 刀杆折弯仿真计算

为了进一步验证理论计算的正确性，应用ANSYS Wrokbench有限元分析软件对刀杆受力折弯过程进行仿真计算。由1.1的分析可知，刀杆的折弯部分需要变形，而折弯部分以外是不需要变形的，所以折弯的仿真采用ANSYS Workbench刚柔耦合动力学分析模块完成。建模时将刚体和柔性体分开建模，通过接触的定义将二者结合到一起，分析时将刀杆的折弯部分设置为柔性体并划分网格，其余部分设置为刚体，如图4所示。

图4 ANSYS Workbench中的刀杆刚柔耦合模型

对于柔性体需要添加材料模型，刀杆材料为42CrMo，材料参数选自参考文献[4]，如表1所示。网格划分和材料模型添加完毕后对模型添加约束和载荷。首先将刀杆刚体部分不与变形体接触的端面添加固定约束；然后在刀杆柔性体不与刚体接触端面且不安装刀片一端施加303 187.656 N的载荷，添加载荷后的模型如图5所示。然后进行仿真计算和结果查看。本文所关心的是刀杆的折弯变形情况，因此添加Total Deformation，查看模型的最大总变形，其最大等效变形云图如图6所示。由图6可以看出刀杆前端的最大等效变形为7.604 7mm，相比于理论变形值6.67mm大了14.01%。这是因为刀杆的截面面积在端面处相对于理论分析值稍小，因此造成了抗弯强度降低，使变形量有所增加，同时考虑在实际的折弯过程中会发生材料的回弹，按照理论计算结果会造成变形不到位的情况，所以对于稍大于理论计算值的变形在实际进行折弯加工是合理的。

表1 42CrMo材料模型参数

图5 添加载荷后的刀杆模型

图6 刀杆最大等效变形云图

2 折弯刀杆加工时的强度分析

2.1 切削力计算

刀杆在工作时主要承受来自刀片加工时的切削力，因此切削力的计算主要根据刀片的结构尺寸确定。对于硬质合金车刀，切削合力可以分解为3个分力，即主切削力Fc、背向力Fp以及进给力Ff。三者的计算公式分别为[5]：

(3)

(4)

(5)

式中：CFc、CFp、CFf为与加工材料、刀具材料和加工形式有关的系数；xFc、yFc、nfc、xFp、yFp、nFp、xFf、yFf、nFf为与加工材料、刀具材料和加工形式有关的指数；KFc、KFp、KFf为修正系数；ap、f、Vc为背吃刀量、进给量、进给速度。

通过查文献[6]可得：

CFc=270；XFc=1.0；yFc=0.75；nFc=-0.15。

CFp=199；XFp=0.9；yFp=0.6；nFp=-0.3。

CFf=294；XFf=1.0；yFf=0.5；nFf=-0.4。

已知弹体材料为58SiMn，材料的强度极限为σb=1 080MPa，由刀尖圆弧半径R=0.8(查表时取1.0)，刀片前角ro=0°，主偏角kr=90°，刃倾角λs=0°，吃刀量ap=0.6mm，进给量f=0.2min/r，切削速度Vc=90m/min，工作效率取9.81，最后可计算得：

Fc=9.81×270×0.61.0×0.20.75×90-0.15×1.332 4≈322.444 3N；

Fp=9.81×199×0.60.9×0.20.6×90-0.3×1.139 2≈138.612 8N；

Ff=9.81×294×0.61.0×0.20.5×90-0.4×2.721 6≈348.184 9N。

2.2 刀杆强度分析

分析时使用UG三维仿真软件进行模型建立并将刀杆和刀片进行装配，然后将UG中装配好的三维模型以STP格式的文件导入到ANSYS Workbench[7]中。模型导入成功后进行材料模型的设置，刀杆的材料为42CrMo，材料参数见表1，刀片的材料为硬质合金，材料参数如表2所示。材料模型设置后分别赋给刀杆和刀片，并给模型划分网格，共划分177 249个节点、124 018个单元。划分后的模型如图7所示。

图7 划分网格后的刀杆和刀片

表2 硬质合金材料模型参数

网格划分完成后要添加约束和载荷，经分析刀杆在加工内膛时一端为固定端，因此在刀杆的后端面添加固定约束，而在加工过程中刀片为承受切削力的部件，前面已经经过理论计算，因此在刀片的刀尖处添加力，然后将理论计算得到的受力值添加到x、y、z三个方向，添加约束和载荷后的模型如图8所示。之后进行有限元计算并添加Total Deformation以及Equivalent Stress来查看最大等效变形和等效应力。二者的云图如图9和图10所示。

图8 添加约束和载荷后的模型

图9 刀杆和刀片的最大等效变形云图

图10 刀杆和刀片的最大等效应力云图

由图9可以看出，在进行内膛切削过程中，刀杆的最大等效变形为0.258 58mm，出现在刀杆切削的一端。这是因为在进行切削过程中整个模型近似为一个悬臂梁，受力一端变形最大；而从图10可以看出，模型的最大等效应力值为330.11MPa，出现在刀片与切削端相对一侧的刀杆位置。这是因为刀片工作时受力很大产生变形后，导致刀片与刀杆接触，二者在切削力作用下相互作用，且刀杆在该位置有一个易产生应力集中的棱角，因此造成该部位所受到的应力最大。从计算结果来看，刀杆所受的应力小于材料的屈服极限，变形也很微小，所以在正常的工作状态下，折弯刀杆能够满足对某型弹体的内膛加工要求。

3 折弯刀杆加工及内膛车削应用

经过上面的分析，折弯刀杆的结构设计合理，工作状态能够满足要求，因此可以在原内膛车刀刀杆的基础上进行折弯加工。加工时采用某型50t压力机对刀杆进行下压加工，根据理论计算可知压力值为303 187.656N，所施加的压力约为30.937t。由于此数据精度较高，手动调节很难达到，所以实际加压时采用31t的压力对刀杆进行加工，加工后由于材料的回弹量大于仿真时的预估值，因此对刀杆的折弯部分进行了多次打磨和内膛切削验证才达到了设计要求。图11为经过压力机折弯加工并打磨后的刀杆。