基于主成分回归分析法的导水裂缝带高度预测
2021-10-26曹始友成文举张历峰徐德宝陈大林尹会永
曹始友,成文举,张历峰,徐德宝,王 松,陈大林,王 鹏,尹会永
(1.枣庄矿业(集团)有限责任公司,山东 枣庄 277100;2.山东科技大学地球科学与工程学院山东省沉积成矿作用与沉积矿产重点实验室,山东 青岛 266590;3.枣庄矿业(集团)有限责任公司滨湖煤矿,山东 枣庄 277599;4.枣庄矿业集团新安煤业有限公司,山东 济宁 277607;5.枣庄矿业(集团)付村煤业有限公司,山东 济宁 277605;6.枣庄矿业(集团)有限责任公司蒋庄煤矿,山东 枣庄 277519;7.山东省三河口矿业有限责任公司,山东 济宁 277600)
煤层开采后,围岩的原始应力平衡被打破,顶板上覆围岩发生移动变形,极易形成裂缝,进而发育成为地表水及地下水运移的通道[1-3]。依据现有的“上三带”理论[4-5],冒落带及裂隙带共同组成的导水裂缝带成为煤层顶板突水危险性的决定性因素,即原始状态隔水层的隔水性是否在开采过程中遭到采动的破坏。影响导水裂缝带发育高度的因素有很多,大部分可进行定量描述,但有些只能进行定性说明[6-8]。目前,研究认为其主要影响因素有上覆岩层性质、煤层厚度、开采深度、工作面倾向长度、顶板厚度及煤层倾角;另外,开采时间、重复采动等也会对导水裂缝带高度产生影响。如何高精度地预测顶板导水裂缝带发育高度,一直是许多科技工作者和现场工程技术人员工作研究的重点问题之一。
目前对于导水裂缝带高度预测的方法仍以《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》[9]所提供的经验公式法为主,但随着开采方式的变化及开采难度的增大,原有的经验方法已不能完全满足生产的需求。目前国内的学者及科技工作者对于导水裂缝带高度的预测方法也做了一定的探索和研究,提出了一些具有实用价值的新方法,如:量纲分析法、PSO-RBF神经网络模型、偏最小二乘回归法、基于最小二乘法的PLS-BP神经网络模型、支持向量机模型、模糊聚类支持向量机模型等[10-15],另外还有SAS数学软件[8]及多方法综合预测[16]等。相较于传统的预测方法,新的模拟模型及综合方法在特定条件下具有更高的准确性和针对性,但模型方法较为复杂,参数选取主观性较大;多方法综合确定需要较大的工作量,仍具有一定的不足。主成分分析,也称主分量分析,是通过降维的方式将多指标通过一定的重新组合转化为少数几个综合指标,即所谓主成分,用以解释资料的综合性指标[17-18]。本文基于蒋庄煤矿及其周边多个煤矿的矿井资料,选取了影响导水裂缝带发育的主要影响因子,利用主成分分析法及MATLAB数据处理软件,结合回归模型检验[19],建立蒋庄煤矿导水裂缝带发育高度的回归模型,对煤矿导水裂缝带高度的预测方法的研究和应用具有一定的借鉴意义。
1 方法和原理
主成分分析是在给定的一组相关变量的基础上,通过一定的线性关系,将其转换成另一组按照递减方差的顺序排列的不相关变量,确定各变量的主成分,在此基础上建立起与实际相关的回归模型。主成分分析法在水质评价方面具有较广的应用,参照类比的思想,通过分析影响导水裂缝带高度的主要因素,将其运用到导水裂缝带高度的预测中,通过确定几个最主要的影响因素,来替代原有非必要指标,从而达到减少任务量的目的。其主要的计算步骤如下所述。
1) 构建数据矩阵并标准化处理。设有n个矿区样品,每个矿区样品有p个主要影响因素,将原始数据写成矩阵,见式(1)。
[X1,X2,…,Xp-1,Xp]
(1)
2) 标准化处理。由于不同指标的量纲不同,在计算方差会产生很大的误差,对判断主成分具有较大的影响,因此需要将选用指标进行无量纲化处理,即标准化,其公式见式(2)。
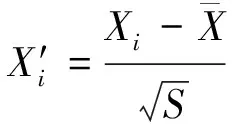
(2)

3) 计算相关系数矩阵,见式(3)。

(3)
式中,rij(i,j=1,2,…,p)为原变量xi与xj的相关系数,rij=rji,其计算公式为式(4)。

(4)
4) 计算特征值与特征向量。
①解特征方程|λI-R|=0,常用雅可比法(Jacobi)求出特征值,并使其按大小顺序排列λ1≥λ2≥…≥λp≥0。


在实际工作中,主成分个数的多少取决于能够反映原来变量85%以上的信息量为依据,即选择累计贡献率不小于85%的主成分个数。
6) 建立回归模型。在确定主成分指标后,通过选取的主成分建立回归模型(式(5))。
Y=a0+a1Z1+a2Z2+…+amZm
(5)
通过上述计算得到了关于Z1,Z2,…,Zm的主成分回归,将主成分式子代入得到关于原指标X1,X2,X3,…,Xp的回归方程(式(6))。
Y=b0+b1X1+b2X2+…+bmXp
(6)
2 实例分析
2.1 研究区概况
蒋庄煤矿位于山东省西南部的滕南矿区,北与程楼断层相接,南接李集断层,西邻高庙断层、徐庄断层,东连尹家洼断层,形成一断裂构造发育,以地堑、地垒为主要特点的宽缓褶皱区,构造发育,断裂构造众多,构造中等偏复杂。地层属华北型沉积,广为第四系覆盖,未见基岩露头。井田主要含水层为二叠系山西组3煤层顶板砂岩含水层、石炭系太原组第三层石灰岩含水层、石炭系太原组第十层灰岩含水层、第四系砂砾层、上侏罗统砾岩含水层、二叠系石盒子组顶部砂岩含水层、二叠系石盒子组底部砂岩含水层、石炭系本溪组第十四层石灰岩含水层及奥陶系石灰岩含水层,富水性不均一[20]。
本文所采用数据来源于蒋庄煤矿及其四周紧邻的多个煤矿,如崔庄煤矿、高庄煤矿、付村煤矿等,所选取煤矿均位于滕州矿区,在岩体力学参数、地质构造及地层分布上有很大的相似之处,因此在对导水裂缝带高度预测的研究过程中,可以利用这些矿井长期生产实践中得到的影响导水裂缝带高度因素的数据加以定量分析,既对蒋庄煤矿导水裂缝带高度的研究具有很高的实用价值,也为其他相似煤矿的导水裂缝带高度预测工作提供了一种可供借鉴的方法。
2.2 主回归方程的建立
在研究蒋庄煤矿导水裂缝带高度发育程度的过程中,参照了蒋庄煤矿及其周边相邻同一区域的12个生产矿井的相关资料,由于这些矿井具有基本相同的顶板管理方法,因此对于导水裂缝带具有主要影响的因子确定为以下6个主要因素:采深、煤层厚度、工作面倾向长度、岩性参数(单轴抗压强度)、顶板厚度及倾角。具体的导水裂缝带高度影响因素量化数值见表1。

表1 导水裂缝带高度主要影响因素量化表Table 1 Quantification table of main factors affecting the height of water-conducting fracture zone
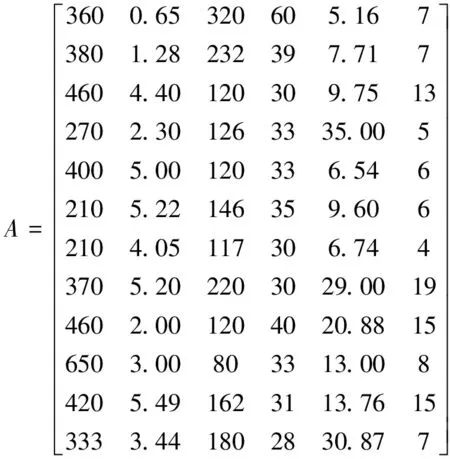
对于上述14个工作面所选取的7个指标分别依次确定为x1、x2、x3、x4、x5、x6、x7,由于所选指标的量纲不同,因此需要对各指标的量纲进行消除,使数据具有可比性,即对数据进行标准化处理。为了研究主成分回归分析对于导水裂缝带高度的预测可靠性,将前12个工作面的数据作为分析数据,将蒋庄煤矿2个工作面数据作为预测结果的验证数据。分析数据构成的矩阵为矩阵A,见式(7)。
第一步:利用MATLAB数据处理软件对式(7)做标准化处理得到标准化矩阵B,见式(8)。
标准化处理之后的7个无量纲指标分别表示为
第二步:经过标准化处理后数据的相关系数矩阵用Rp×p=(rij)p×p表示。由于该矩阵为对称矩阵,因此可以用矩阵B计算得到的相关系数矩阵C,见式(9)。
第三步:求出相关系数矩阵的特征向量和特征值,利用MATLAB软件计算得到具体数值,即矩阵D,见式(10)。
第四步:确定主成分,见式(11)。
通过累计贡献率的大小来选择m(m 表2 主成分特征值和贡献率Table 2 Eigenvalue and contribution rate value ofprincipal component (7) (8) (9) (10) (11) (12) 通过上述四个主成分的基本线性组合可知:第一主成分F1可看作x2的变量,因为其在式中的系数绝对值大于其他变量的系数,即反映了煤层厚度对导水裂缝带高度的影响;第二主成分F2可看作x4和x6的综合变量,反映了岩性、倾角对导水裂缝带高度的影响;F3可看作x5的变量,反映顶板厚度对导水裂缝带高度的影响;F4可看作x1和x3的变量,反映采深、倾向长度对导水裂缝带高度的影响。四个主成分的得分情况见表3。 表3 主成分分布表Table 3 Principal component distribution table 取前四个主成分建立回归方程(式(13))。 y′=a0+a1F1+a2F2+a3F3+a4F4 (13) 采用最小二乘估计可得式(14)。 y′=-0.538 8F1-0.371 1F2+ 0.06F3+0.445 4F4 (14) 对于标准化数据,把各主成分的回归系数还原成关于原自变量的回归系数,经计算得到式(15);将标准化数据还原成原始数据,经过计算得到关于原始数据的回归系数见表4。回归方程式见式(16)。 表4 原始数据回归系数Table 4 Raw data regression coefficient (15) (16) 2.3.1 回归显著性检验 将显著水平α的值定为0.05,通过MATLAB软件计算可以得到F的值为37.646 9,可知F>F1-α,表示拒绝H0,因此认为此差别不大,可能仅由抽样误差所致,存在实验因素不同造成误差的可能,故在统计上成立,回归方程显著;同时计算相关系数r2为0.978 3,数值非常接近1,说明回归方程显著;与F对应的概率p为0.000 5,p<α,回归模型成立。 2.3.2 回归系数显著性检验 通过比较各个变量的t值及其相应的概率,进行t检验,如果相应的概率小于给定的显著水平,则Xi对Y显著的线性作用显示为0,否则为1。采用MATLAB软件得到的计算结果见表5。由表5可知,选取的自变量对因变量有显著的线性作用。 表5 Xi对Y的线性作用Table 5 Linear effect of Xi on Y 2.3.3 残差分析 计算得到用于主成分回归分析的14个工作面导水裂缝带高度的残差依次分别为:2.155 6,-2.709 3,4.650 8,-2.033 0,-3.498 9,0.018 4,0.513 1,-1.694 2,-1.356 1,-0.278 2,-0.306 7,4.538 7。采用MATLAB软件做出残差图,如图2所示。由图2可知,除个别数据距离零点较远之外,其余数据的残差离零点均较近,且所有残差的置信区间均包含零点,这说明回归模型(式(17))能较好地拟合原始数据。 图2 回归方程残差图Fig.2 Regression equation residual plot y=76.370 7-0.023 3x1+6.46x2-0.067 8x3-0.739 3x4-0.495 1x5+0.066x6 (17) 通过上述对蒋庄煤矿周边生产矿井影响导水裂缝带高度的因素进行主成分回归分析,以及回归模型检验分析,得出了回归显著性较强、相对准确合理的回归方程。将已有的蒋庄煤矿3下803工作面、3上603工作面导水裂缝带的量化指标代入回归方程,可以得到导水裂缝带高度,见表6。 表6 实测值与预测值对比Table 6 Comparison of measured value and predicted value 由于蒋庄煤矿工作面顶板多为粗、中、细砂岩、粉砂岩和泥岩,属中硬偏坚硬岩性,因此工作面顶板定为中硬岩层情况考虑,按照国家煤矿安监局制定的《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》的规定,本次蒋庄煤矿两工作面的冒落带及导水裂缝带高度计算公式选取中硬岩性公式[9](式(18)和式(19))。 (18) (19) 式中,∑m为累计采厚。 已知蒋庄煤矿3上工作面煤层采厚3.8 m,3下工作面煤层采厚亦为3.8 m,按式(18)和式(19)计算其冒落带及导水裂隙带高度见式(20)和式(21)。 (20) (21) 通过计算可以得出,按照中硬岩层考虑预计采3上(3下)工作面煤层时,两带高度分别为H冒=8.1~12.5 m,H裂=33.7~44.9 m,实际上工作面顶板为中偏硬岩层,为了使观测方案安全可靠,裂隙带探测高度定为60.0 m,见表7。 表7 实测值与预测值对比Table 7 Comparison of measured value and predicted value 主成分回归分析法可消除回归分析中出现的指标间多重共线关系影响,使所建回归模型更符合实际情况。通过实测数据可知蒋庄煤矿3下803工作面和3上603工作面导水裂缝带高度分别为54.60 m、47.75 m,基于山东滕州矿区12个煤矿的实测数据建立的主成分回归模型,对两工作面导水裂缝带高度预测分别为56.239 1 m、49.102 1 m,预测相对误差分别为3.00%、2.83%;运用经验公式法对两工作面导水裂缝带高度预测结果均定为60.00 m,预测相对误差分别为-9.89%、-25.65%。由以上预测结果可知,主成分回归分析模型方法预测回采工作面的导水裂缝带发育高度较经验公式法具有较高的准确性,可以更好地预测导水裂缝带发育高度。 1) 主成分回归分析法对于数据量较大的实际问题具有较好的数据处理能力,通过降维的处理思想,可以通过将原始具有重叠关系的数据重新组合优化,通过贡献率的大小选定多个主成分,基本代表原有数据的所有信息。 2) 基于山东滕州矿区12个煤矿的实测数据建立的主成分回归模型,对蒋庄煤矿3下803工作面和3上603工作面导水裂缝带高度预测结果分别为56.239 1 m、49.102 1 m,预测相对误差分别为3.00%、2.83%;运用经验公式法对两工作面导水裂缝带高度预测结果均定为60.00 m,预测相对误差分别为-9.89%、-25.65%。 3) 本文受验证数据的数量限制,未能够排除数据量较少带来的误差,但在已有数据的基础上表明,主成分回归分析模型对于蒋庄煤矿的导水裂缝带高度预测符合实际,具有较好的预测精度,可以作为一种导水裂缝带高度预测的辅助方法。









2.3 回归模型检验分析


3 蒋庄煤矿导水裂缝带发育高度预测
3.1 主成分分析回归模型

3.2 经验公式法





3.3 结果分析
4 结 论
