基于变权综合灰靶模型的采空区风险等级评价
2021-10-26江慧敏叶义成胡南燕王其虎吴孟龙
江慧敏,叶义成,2,胡南燕,王其虎,陈 虎,吴孟龙
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.湖北省工业安全工程技术研究中心,湖北 武汉 430081)
随着矿产资源的持续开采,形成了大量的地下采空区[1-3]。这些采空区是诱发地表塌陷、顶板大规模冒落和井下透水的主要危险源[4-6],已成为矿山安全生产的重大风险,严重威胁矿区作业人员与财产的安全。因此,有必要对采空区进行风险评价与预测,为有效防控采空区风险提供依据。
目前,专家学者针对矿山采空区风险等级评价的研究较多。黄亮等[7]将偏序集引入采空区塌陷风险等级评价,解决了指标赋权争议问题;汪伟等[8]采用改进的物元可拓模型对采空区稳定性进行评价,评价结果较模糊模型准确度更高;ZHOU等[9]将粒子群算法和支持向量机算法用于采空区风险等级评价并取得很好的效果;唐胜利等[10]构建了空洞型采空区稳定性评价的BP神经网络模型并验证了其准确性;赵超等[11]采用基于层次分析的可拓法对采空区进行危险性评价并建立了分级标准。在这些方法中,物元分析法在处理不确定多指标问题时效果不是很理想[7,12],神经网络法、支持向量机建模所需样本量较大,不能较好地克服评价指标间相关性信息重叠的不足,对评价结果将产生一定的误差[13]。因此,需要研究针对采空区风险等级评价样本量小、评价指标权重难以客观确定等特点的评价方法。
1982年,我国学者邓聚龙首次提出灰色系统理论,并最早提出了灰靶思想。灰靶多指标风险评价方法是在灰色理论基础上发展的一种评价方法,其算法简洁,所需样本量小,能很好地解决多指标的不确定性问题。目前,灰靶评价方法已应用到多个领域研究[14]。周鑫隆等[15]采用灰靶评价方法,解决了岩爆烈度等级预测问题;梁冰等[16]通过构建多指标加权灰靶决策模型应用于煤与瓦斯突出可能性评价;高彩云等[17]基于灰靶评价理论,将滑坡灾害危险性评价定量化。随着灰靶理论的发展与丰富,其应用领域不断拓展,将灰靶风险评价方法应用到采空区风险等级评价是其应用拓展的有效方向之一。
采空区风险等级评价中,在确定影响因素权重时多采用直接评判法、德尔菲法(Delphi)、多比例两两对比法、重要度系统评分法和层次分析法等常权计算,利用理论基础结合发挥专家经验的采空区风险等级划分,不能客观地判断评价指标的重要程度,影响评价结果的准确性[18]。灰熵关联分析引入平衡函数计算采空区风险因素的权重,避免了单一权重计算方法的片面性,通过实现权重计算的动态平衡,调整影响采空区风险各因素在评价中作用,使权重的计算更加客观科学。
基于此,选取已有金属矿采空区风险等级评价样本,采用灰靶评价方法,借助灰熵关联分析法并引入平衡函数计算变权综合权重,得到不同采空区风险等级的靶心距范围,构建采空区风险等级靶距图,根据采空区风险等级靶距图对检验样本进行风险等级划分。
1 采空区风险等级评价样本矩阵构建
1.1 评价指标确定
以往采空区风险等级评价指标的选取强调危险源与管理之间的平衡,侧重于管理,而预防采空区事故发生应从根源出发。为使建立的评价指标体系与致灾机理上存在对应关系,从采空区固有属性出发,考虑从岩体物理力学参数、采空区结构参数、空区群影响系数三个方面选取评价指标,兼顾评价指标选取的全面性、代表性、合理性等原则。参考杨彪[19]、陈娇等[20]的研究成果,选取对采空区风险等级评价影响较大的8个指标。对采空区风险等级评价指标进行多层次分解,将采空区风险等级评价作为A层,岩体物理力学参数、采空区结构参数和空区群影响系数作为B层指标。其中,空区群影响系数是由采空区所处的地质情况(层理、节理、埋深、水文等)、开采方法、空区形态、矿柱特征等决定。根据采空区风险分析的内容和需要评价的对象特点,选取岩石单轴抗拉强度、内摩擦角、弹性模量为岩体物理力学参数的C层指标,选取采空区埋藏深度、空区顶板面积、空区体积、采空区宽高比为采空区结构参数的C层指标。特别需要说明的是,由于B层评价指标空区群影响系数是具体的参数,未再进行多层次分解,其本身也是C层指标,构建的采空区风险等级评价指标体系如图1所示。

图1 采空区风险等级评价指标体系Fig.1 Goaf risk assessment index system
1.2 评价样本矩阵构建
设多指标风险等级评价问题有m个样本Ai(i=1,2,…,m),m个样本对应的t个风险等级组成的评语集yk(k=1,2,…,t),n个评价指标vj(j=1,2,…,n),则样本指标矩阵为X={xij}(i=1,2,…,m,j=1,2,…,n)。
由于各指标的度量标准及量纲不同,需要对样本指标矩阵进行标准化处理。vj一般情况下可分为“成本型”和“效益型”。大部分数据序列的标准化处理是将评价指标映射到[0,1]区间上,为了有利于数据序列在优于或劣于平均水平时赋予更准确地值,应用线性奖优罚劣变换算子,将[0,1]区间扩展成[-1,1][21]。设Cj为各评价指标下样本的平均值,见式(1)。
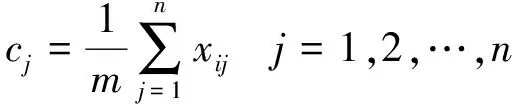
(1)
对于成本型指标,计算见式(2)。
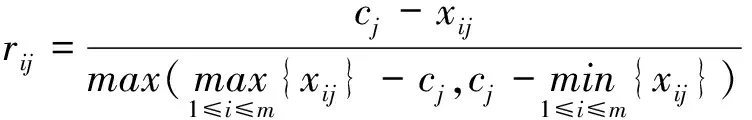
(2)
对于效益型指标,计算见式(3)。
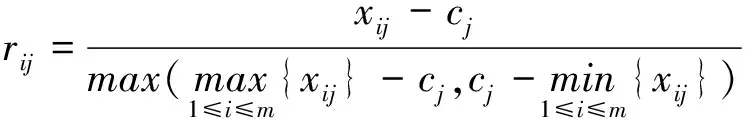
(3)
根据式(1)~式(3),将样本指标矩阵X标准化后得到评价样本矩阵R={rij}(i=1,2,…,m,j=1,2,…,n)。
根据文献[19]中的金属矿采空区样本,选取15个采空区样本数据作为学习样本。该文献中将样本数据的采空区稳定性分为4级,且采空区稳定性随着划分等级的增大而增大。这里为适应采空区风险等级评价对应将文献中采空区稳定性分级进行转化,使采空区风险随着评价等级的增大而减小,从而得到学习样本的实际风险等级状况,等级转化后的学习样本数据见表1。

表1 学习样本数据Table 1 Learning sample data
岩石单轴抗拉强度、内摩擦角、弹性模量、采空区宽高比属于效益型指标,采空区埋藏深度、空区顶板面积、空区体积、空区群影响系数属于成本型指标。评语集yk即为采空区风险等级区间划分,属于效益型指标,其为不等间距的数据划分。为使评语集yk的标准化更科学合理,对yk进行指数化处理。根据yk的分布特征,设yk满足yk=eφ-1,则φk为各评价等级的对应系数。由式(1)~式(3)得到评价样本矩阵R,结果见表2。

表2 评价样本矩阵RTable 2 Assessment sample matrix R
2 变权综合灰靶模型建立
2.1 变权综合权重计算
采空区风险受多种因素影响,根据各影响因素的属性特征,应用灰熵关联分析法计算权重,并引入平衡函数对权重进行动态调整,最后得到变权综合权重[22-24]。灰熵关联平衡函数的变权综合权重计算方法能更客观地反映影响采空区风险各因素在评价中的作用。
设δij为样本指标矩阵标准化后评价样本矩阵R和评语集yk间的灰色关联系数,其计算见式(4)。
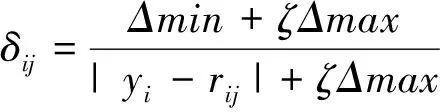
(4)
式中,Δmax和Δmin计算分别为式(5)和式(6)。
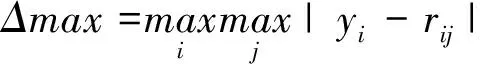
(5)
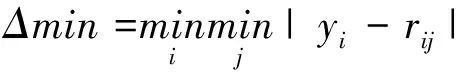
(6)
Δmax和Δmin为两级最大和最小差值。ζ为分辨系数,ζ∈[0,1],ζ的取值大小需要准确地反映评价样本矩阵R的整体性,因此不能过大也不能太小,计算公式见式(7)和式(8)。
(7)
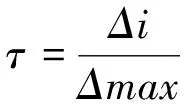
(8)
ζ的取值区间计算公式见式(9)和式(10)。
Δmax>3Δi,τ≤ζ≤1.5τ
(9)
Δmax<3Δi,1.5τ≤ζ≤2τ
(10)
设αj为第j个评价指标的灰色关联度,计算见式(11)。
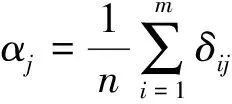
(11)
设Pij为灰色关联系数的概率分布值,计算见式(12)。
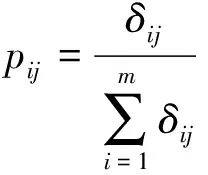
(12)
评价指标灰关联熵值Hj,计算见式(13)。
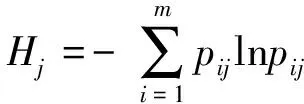
(13)
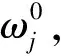

(14)
其中,Hmax=lnm为由m个样本组成的评价样本矩阵R的最大熵[25]。在得到评价指标灰色熵权后,引入平衡函数的变权模型如下所述。
设βj为第j个评价指标的测量值,则平衡函数可以表示为式(15)。
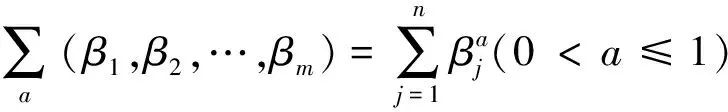
(15)
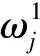
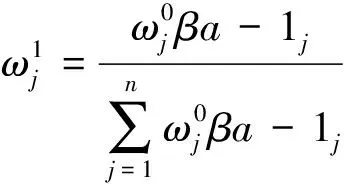
(16)
式中,a为选择评价指标影响程度的参数。
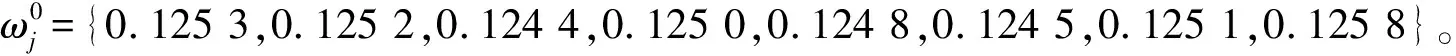
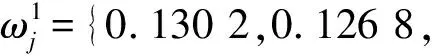
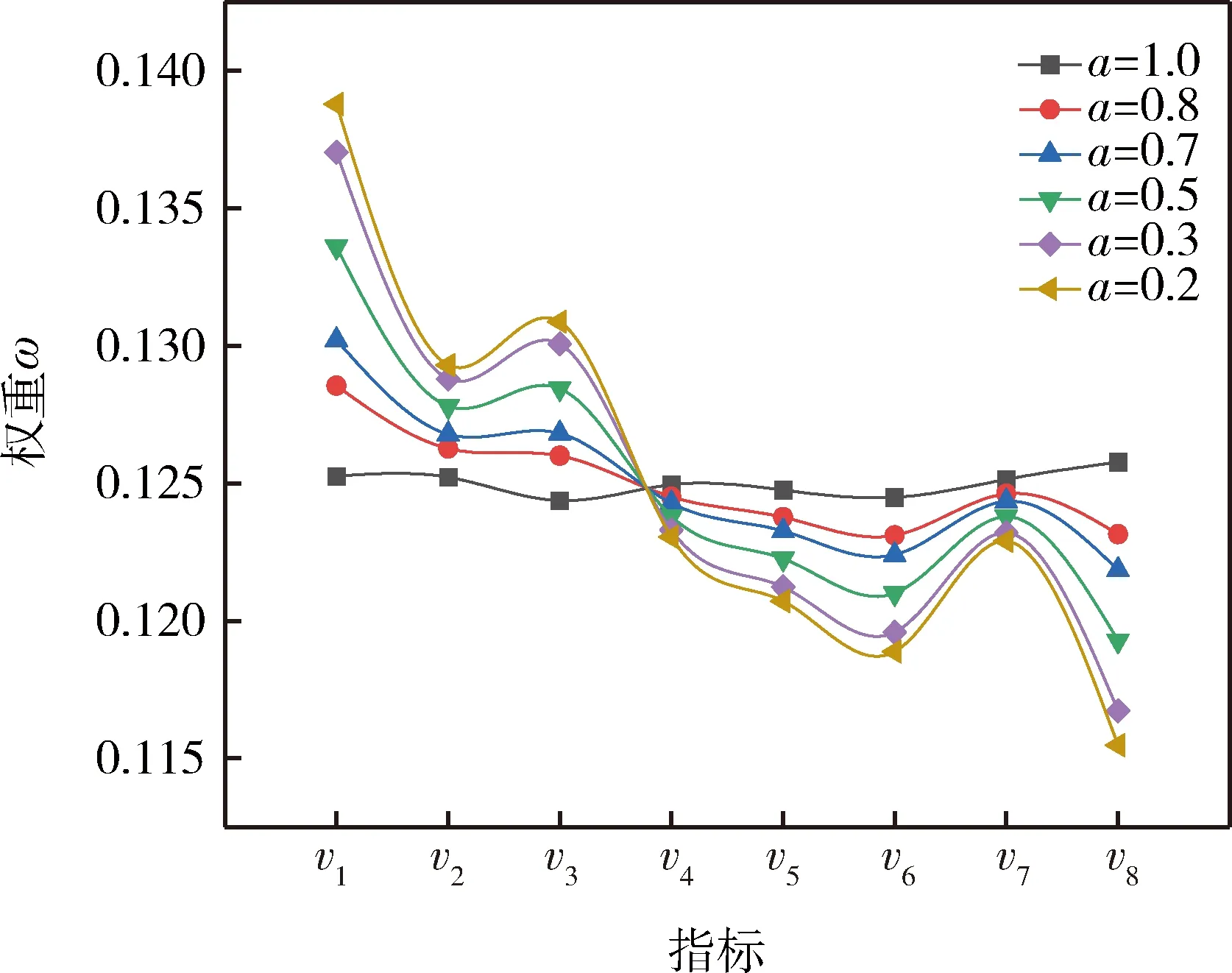
图2 a的不同取值下的权重Fig.2 The weight of a different value of a
2.2 风险等级靶距图建立
2.2.1 靶心距的计算
靶心距ei反映的是评价方案的优劣性,ei越大,表示第i种方案越接近最优情况;ei越小,则表示评价方案越接近最差情况。

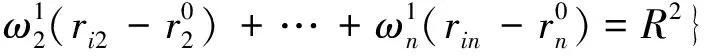
(17)
其中r0=max{rij|1≤i≤m|}(j=1,2,…,n)为变权综合灰靶模型的最优效果向量,即为靶心。
定义ei为评价方案针对评价指标vj的靶心距,计算公式为式(18)。
ei=|rj-r0|=
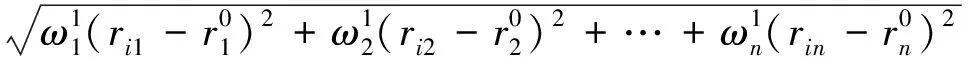
(18)
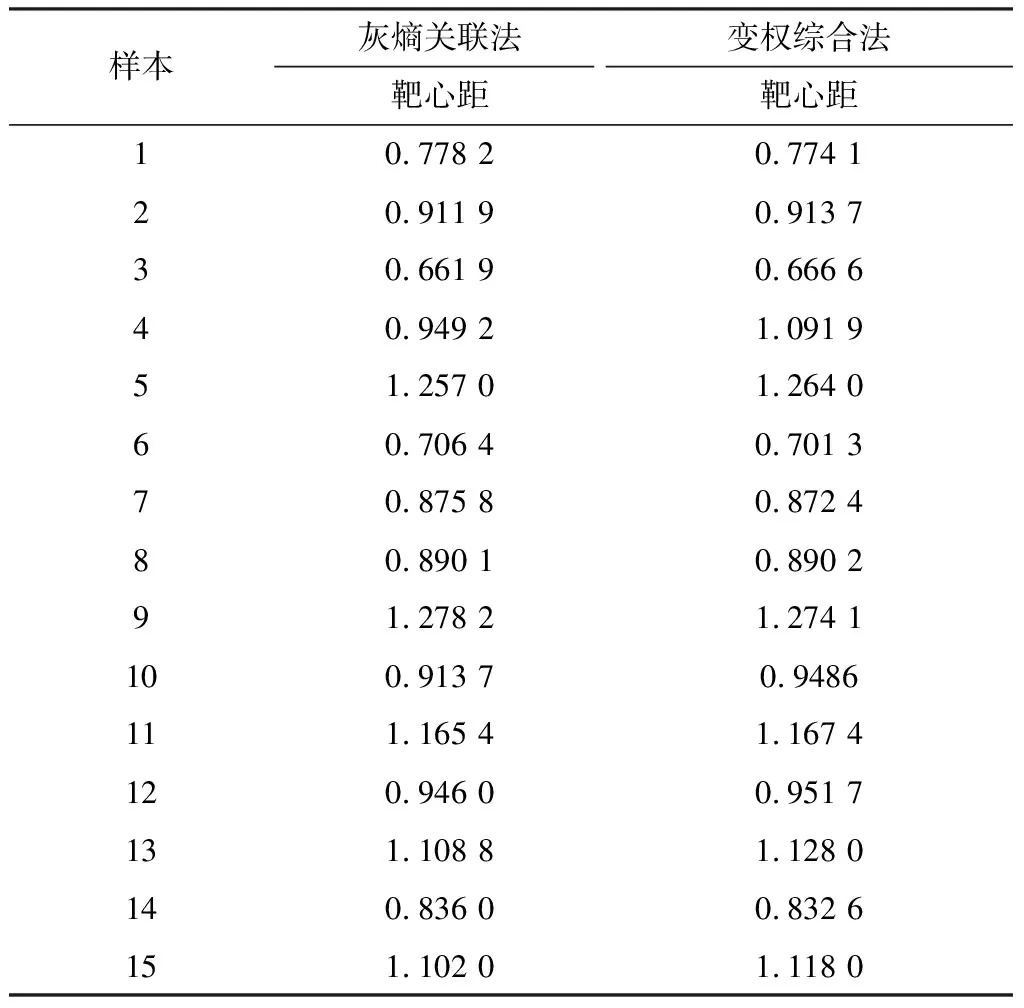
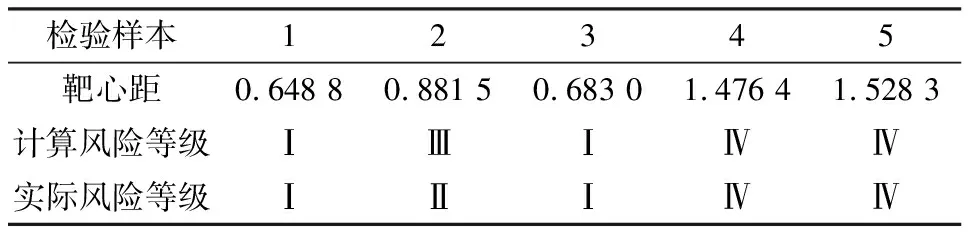
设集合E为各评价样本的靶心距的集合,即:E=(e1,e2,…,em),集合D为集合E根据t个风险等级的有序划分区间,即D=(d1,d2,…,dt),令1≤ψ lψ=μγψ+(1-μ)ηψ+1,μ∈(0,1) (19) Y={d|0≤d1 lt-1≤dt<+∞} (20) 2.2.2 靶距图的建立 由式(17)和表2可知靶心r0={0.838 4,0.578 9,0.516 0,1.000 0,0.686 7,0.652 4,0.892 3,1.000 0},根据式(18)可以得到15个学习样本的靶心距ei,见表3。 表3 靶心距计算结果Table 3 Target distance calculation results 确定靶心距后,根据式(19)和式(20)的等级划分标准,对采空区风险等级进行划分,共划分为4级,见表4。 表4 采空区风险等级划分Table 4 Risk classification of goaf 根据采空区风险等级划分情况,构建采空区风险等级靶距图,如图3所示。检验样本可根据其靶心距在采空区风险等级靶距图上的分布确定风险等级。 图3 采空区风险等级靶距图Fig.3 Target distance map of risk level in goaf 铜坑矿位于广西省南丹县大厂镇境内,矿山开采对象主要包括上部细脉带矿体,中部及下部的91#矿体、92#矿体,三个矿体位置在空间上呈立体重叠分布,地质赋存条件复杂。1980年代初,矿山投产初期开采的矿体为细脉带矿体的上部,采用无底柱分段崩落法回采;对矿体下部570~625 m矿段进行开采时,采用分段空场嗣后水泥砂浆胶结充填法回采;对该矿体的底部505~570 m矿段进行开采时,采用空场法回采。到2003年底,完成了8#矿体、4#矿体、79#矿体、1#主矿体等采场的矿石回采作业。细脉带矿体经过30多年的开采形成了大量的采空区,局部地段采空区的冒落和坍塌已成为威胁矿山安全生产的重大隐患。根据铜坑矿采空区实际情况,选取文献[19]中的5组实测数据作为检验样本,该采空区数据是以实测采空区信息为基础,运用数值模拟手段,开展实测空区危险度定级数值分析,并在空区形态综合分析的基础上所获得的空区数据信息,见表5。 表5 检验样本数据Table 5 Examine sample data 表6 靶心距计算结果及风险等级对比结果Table 6 Comparison between target distance calculation 由表6可知,变权综合灰靶模型评价结果与实际风险等级一致[19],检验样本的实际风险等级是根据地质资料及探测信息获得确定的,这表明采用变权综合灰靶模型进行采空区风险等级评价是可行的。因此,灰靶多指标风险评价方法适用于采空区风险等级评价研究。 为进一步分析变权综合灰靶模型的合理性和准确性,把灰熵关联分析方法作为定权方法,将基于灰熵关联分析方法与变权综合权重计算方法的灰靶模型评价结果进行对比。采用不同权重计算方法得到学习样本的灰靶模型靶心距结果见表7。 表7 学习样本的靶心距结果对比Table 7 Comparison of target distance results oflearning samples 表8 基于灰熵关联分析方法的采空区风险等级划分Table 8 Risk classification of goaf based ongrey entropy correlation analysis 表9 基于灰熵关联分析方法的检验样本结果及风险等级对比Table 9 Comparison of test sample results and risk levelsbased on grey entropy correlation analysis 1) 针对采空区风险定量评价的影响因素具有复杂性和信息不完整且具有相对完整信息的采空区样本量小的特点,构建了采空区风险等级评价的变权综合灰靶模型,克服了采空区风险等级评价指标不确定性的问题。 2) 建立了灰熵关联分析及平衡函数的变权综合指标权重确定方法。由灰熵权重引入平衡机制,修正个别灰熵权重的偏离,使各指标权重得到平衡,保证了指标权重选取的客观性与可靠性。 3) 选用15个学习样本建立变权综合权重及风险等级靶距图并对5个检验样本进行变权综合灰靶模型有效性检验,检验结果与实际风险等级一致,并将基于灰熵关联分析方法与变权综合权重计算方法的灰靶模型评价结果进行对比,证明了变权综合灰靶模型的合理性和准确性,表明采用变权综合灰靶模型进行采空区风险等级评价是合理可行的。 4) 变权综合灰靶模型考虑了采空区风险影响指标及其权重的客观性、合理性分配,量化的评价结果可对采空区的风险进行有效的等级划分,该方法所需样本量较小,计算简单,为采空区风险等级定量评价提供了一种有效途径。

3 有效性检验
3.1 结果验证

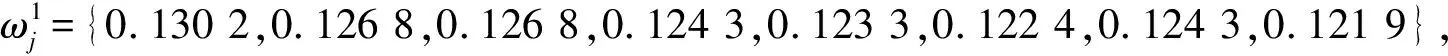

3.2 对比分析

4 结 论
