中低速磁浮单线轨道梁日照温度场分析★
2021-10-26刘德军梅甫良
刘德军,梅甫良
(嘉兴学院建筑工程学院,浙江 嘉兴 314001)
0 引言
磁悬浮列车是一种无接触的电磁悬浮、导向和驱动的列车系统,它依靠电磁吸力或电动斥力将列车悬浮于空中,具有安全、环保、经济等特点。目前,中国正在大力发展磁浮交通,时速600 km高速磁浮列车已在青岛下线,长沙中低速磁浮快线运营速度已提速至140 km/h,磁浮将是中国高铁之后走向世界的又一张亮丽的“国家名片”。然而,磁浮列车的悬浮间隙一般在8 mm左右,对轨道梁的平顺性要求极高,而温度作用是影响其不平顺的重要因素之一。另外,磁浮交通大量采用高架桥梁,其中比例最大的中小跨度简支梁和连续梁大多采用单线箱梁方案[1]。现行的CJJ/T 262—2017中低速磁浮交通设计规范等在计算温度效应时是按照现行TB 10002—2017铁路桥涵设计规范和TB 10092—2017铁路桥涵钢筋混凝土和预应力混凝土结构设计规范的温度梯度模式取值的,但由于磁浮车辆是“抱轨”运行,轨道梁的宽度一般为1.3 m~1.5 m[2-3],其几何尺寸与传统铁路桥梁差异很大,传统铁路桥梁的温度梯度模式是否适用于单线磁浮轨道梁还需要进一步研究。因此,开展磁浮轨道梁温度场的研究,对磁浮交通的发展和应用具有重要的意义。
国内外学者对混凝土箱梁的日照温度场进行了大量的研究,文献[4]对桥梁结构日照温度作用研究的国内外现状及展望进行了全面的分析和总结,相对于传统公路和铁路箱梁,针对磁浮交通轨道梁的温度场研究还不足。乔柏平等[5]、李玉磊[6]、顾芸等[7]采用ANSYS软件对上海高速磁浮轨道梁的温度场进行了数值模拟分析,提出了该类截面的温度梯度分布模式。徐钢[8]则采用现场实测与数值模拟相结合的方法研究了桥梁走向、气象参数等因素对箱梁截面温度场的影响。邹波等[9]采用ANSYS对单箱双室高速铁路箱梁进行了二维温度场分析,拟合了温度梯度并与规范进行了对比。莫然[10]则对组合式轨道梁进行了温度场的三维数值模拟,对该类截面的温度特性进行了分析。黄全成等[11]针对磁浮“梁上梁”轨道梁结构型式,对下部大箱梁的温度场进行了数值模拟,对比分析了地域对温度梯度的影响。
上述针对磁浮轨道梁的研究虽然取得了较好的成果,但上海磁浮轨道梁的截面与目前已建成的长沙磁浮快线、清远磁浮单线轨道梁有较大的差异,而邹波,黄全成等所研究的截面,其几何尺寸与传统铁路桥梁相当。因此,本文以目前中低速磁浮交通中广泛采用的单线箱形轨道梁为研究对象,研究其在日照作用下的温度分布特征,对比现有规范温度梯度模型的差异,为单线磁浮轨道梁的温度效应分析提供参考。
1 日照温度场的基本理论
实际上,磁浮单线轨道梁结构日照温度场是三维瞬态温度场,但是沿其轴线方向传热量相对很小,热量传递主要发生在其横截面内,因此可简化为一个无热源二维瞬态温度场,其热传导方程为:
(1)
其中,T(x,y,t)为轨道梁内的温度;λ为轨道梁材料的热传导系数;c为轨道梁材料的比热容;ρ为轨道梁材料的密度;x,y均为轨道梁横截面内的直角坐标;t为时间[12]。
轨道梁外表面除了与其周围接触空气流体的对流换热作用之外,还要受到太阳日照辐射作用以及天空大气逆辐射、地面反辐射、轨道梁自身辐射等辐射换热作用,考虑上述综合作用之后,可写成如式(2)所示的第三类边界条件:
(2)
其中,n为轨道梁表面法向;as为轨道梁材料热辐射吸热系数;qs为投射到轨道梁外表面的总太阳辐射强度;hc为轨道梁外表面与其周围空气流体之间的热交换系数;hr为轨道梁外表面的辐射换热系数;Ta为周围空气温度。
为了方便计算,将式(2)改写为:
(3)
其中,Tz为轨道梁外的综合气温,Tz=Ta+asqs/(hc+hr)。
轨道梁内部没有太阳辐射,但其内表面间存在辐射换热,以及内部空气与混凝土表面存在对流换热作用,考虑上述综合作用之后的内部边界条件为:
(4)
其中,hci为轨道梁内表面与轨道梁内部周围空气流体之间的热交换系数;hri为轨道梁内表面的辐射换热系数;Tai为轨道梁内的周围空气温度。
2 日照温度场的有限元模型及参数
以上海某磁浮简支轨道梁南北走向段为工程背景,该梁跨中截面梁高2.1 m,顶板和底板厚度分别为0.22 m和0.30 m,腹板厚度0.26 m,如图1所示。
2.1 有限元模型
采用ANSYS软件建立日照温度场分析模型。由于轨道梁的走向为正南正北走向,采用平面模型进行研究。模型采用热分析平面单元Plane55,单元总数为964,节点总数为1 008,如图2所示。

2.2 计算参数的确定
2.2.1 轨道梁材料参数
该预应力混凝土轨道梁的强度为C50,其热传导系数λ、比热容c和密度ρ根据《民用建筑热工设计规范》分别取1.74 W/(m·K),0.92 kJ/(kg·℃)和2 500 kg/m3。
2.2.2 气温日过程
气温是影响混凝土桥梁结构温度分布的重要参数,在缺乏实测资料的情况下,轨道梁所处的大气温度日变化过程可采用正弦函数表描述,即:
(5)
其中,Tav为日平均气温,Tav=(Tamax+Tamin)/2;Tam为气温日变幅,Tam=(Tamax-Tamin)/2;Tamax,Tamin分别为日最高气温和最低气温,根据李玉磊的研究结论分别取36 ℃和20 ℃;t0为出现最高气温滞后时刻,假定最高气温出现在15:00,则t0=9。
对于箱梁内部空气,其温度在1 d内波动较小,因此近似按(Tav+1.5)℃计算。
2.2.3 综合换热系数
箱梁外表面与周围大气间进行着对流换热和辐射换热。综合换热系数为对流换热系数和辐射换热系数之和。
对流换热是一个比较复杂的现象,与多种因素相关,通常根据试验研究和经验公式来确定。本文采用由凯尔别克提出的经验公式来计算对流换热系数,其可以表示为风速的函数。
顶板:
hc=3.83v+4.67
(6)
底板:
hc=3.83v+2.17
(7)
腹板:
hc=3.83v+3.67
(8)
其中,v为风速,上海夏季可取3.5 m/s;对于箱梁内部,其对流换热系数一般取3.5 W/(m2·℃)。
辐射换热系数为混凝土结构表面温度和周围大气温度的函数,其系数可表示为:
hr=0.88[4.8+0.075(Ta(t)-5)]
(9)
2.2.4 太阳逐时辐射强度的计算
对日照作用下的轨道梁,其外表面受到太阳直接辐射、太阳散射辐射、地面反射辐射、由天空逆辐射和轨道梁结构自身组成的有效辐射等四部分作用。计算日期取7月15日,上海为东经121.43°北纬31.17°,地面反射辐射系数为0.2,地方透明度系数为0.65,大气辐射系数为0.82,混凝土辐射系数为0.9。根据太阳辐射强度理论和上述气象地址走向参数,可得到轨道梁顶板、底板、东西直腹板外表面和箱梁内部的逐时太阳辐射强度随时间的变化曲线如图3所示。
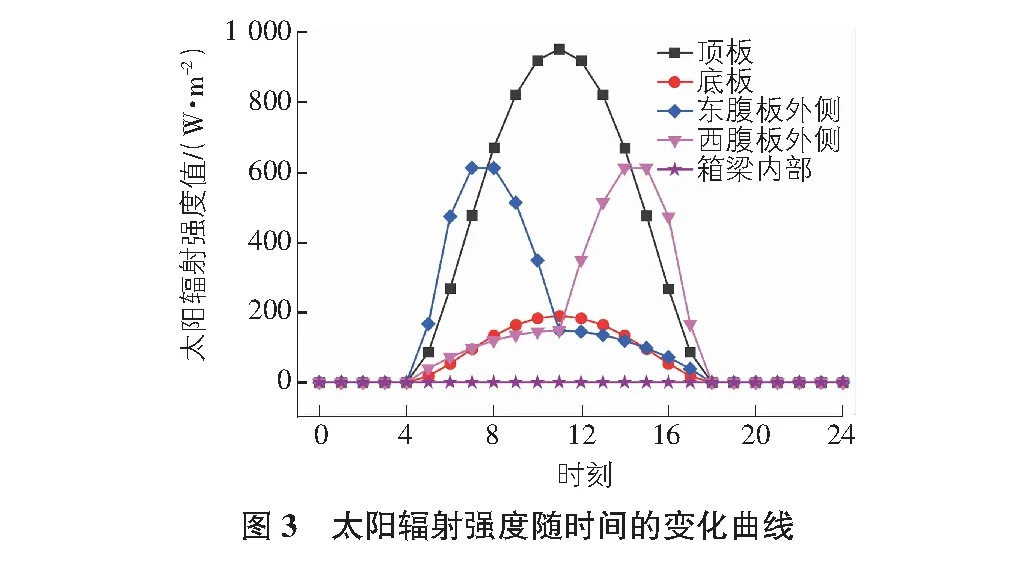
3 计算结果与分析
基于上述理论及参数,对箱梁进行瞬态热分析,计算步长为1 h。为了消除轨道梁初始温度的影响,共循环计算了12 d,取第12天共24 h的结果进行分析。
3.1 截面温度云图
典型时刻轨道梁截面的温度云图如图4所示。由图4可见,随着太阳辐射角度的变化,轨道梁截面的温度分布也发生了相应的变化。早上太阳升起后,东腹板和顶板的温度逐渐升高,在14:00及以后西侧腹板的温度大于东侧腹板。整个轨道梁截面的温度最大值为50.02 ℃,于14:00出现在顶板靠西腹板区域。对于底板和箱梁内部,其温度变化较小。
3.2 截面温度时程
为了研究轨道梁横向和竖向断面温度随时间的变化规律,选取了顶板、底板、左腹板和右腹板厚度中线断面的典型位置,如图5所示,对应位置的温度随时间的变化曲线如图6所示。
由图6(a)和图6(b)可以看出,东西两侧腹板外表面节点T1,T5,B1,B5的温度随时间的变化较大,而中间位置节点T2~T4,B2~B4的温度随时间的变化较小,这是由于外表面受到的辐射比中间位置大。由于太阳直接辐射时间的不同,东西腹板外表面节点达到最高温度的时间也存在明显的差别,东腹板表面节点T5,B5达到最高温度的时间为10:00~11:00,而西腹板表面节点T5,B5达到最高温度的时间为16:00。



由图6(c)和图6(d)可以看出,顶板表面节点WL1,WR1的温度随时间的变化最为显著,离顶板表面0.11 m位置的WL2,WR2节点变化量次之,位于底板表面节点WL5,WR5的变化量再次之,变化量最小的是位于截面高度一半位置和靠近底板表面的节点。除了温度幅值外,达到温度最高的时刻也不相同。对于顶板和底板外表面,温度达到最高的时刻分别为14:00和15:00,而其余中部位置节点则有较大的差异,特别是西腹板断面,中间位置WL2,WL3,WL4温度达到最大值的时刻滞后至17:00~19:00。
3.3 截面竖向温度梯度
基于以上分析结果,左腹板(Ⅰ-Ⅰ断面)、右腹板(Ⅱ-Ⅱ断面)和截面中部(Ⅲ-Ⅲ断面)竖向最大温差均出现在14:00左右,其温度沿高度的变化及与现行规范TB 10092—2017铁路桥涵混凝土结构设计规范所规定的温度对比如图7所示。
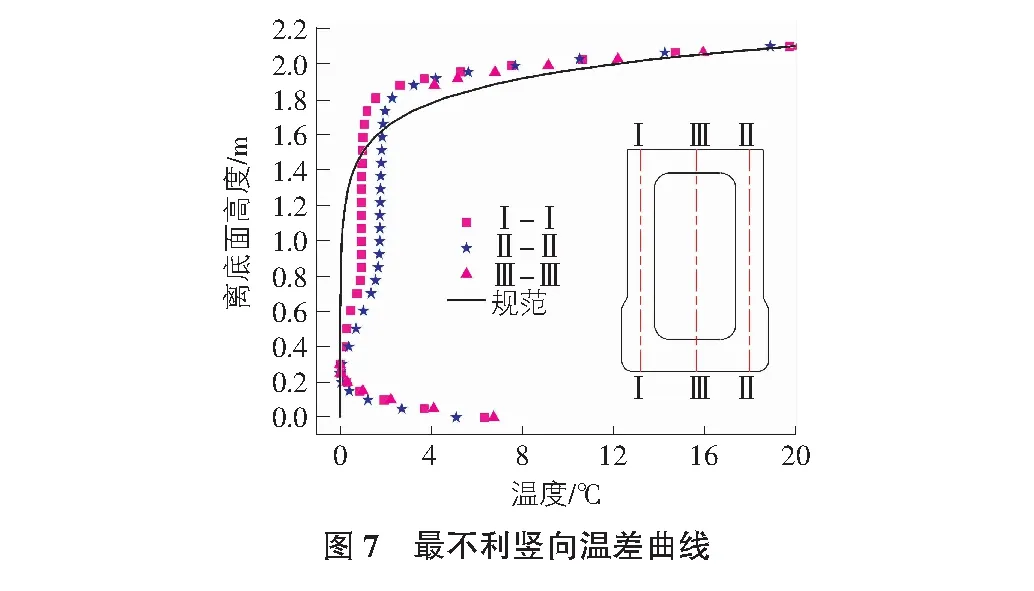
由图7可知,3个断面的温度随高度的变化规律基本一致。左腹板、右腹板和中部断面的最大温差分别为19.8 ℃,18.9 ℃和20.1 ℃;从顶面向下约0.3 m范围内温度急剧下降,在距顶面0.3 m~1.2 m范围内基本保持在1 ℃~2 ℃不变,在距顶面1.2 m~1.8 m范围内温差逐渐减小至0,但在距顶面1.2 m~1.8 m(从底面向上0.3 m~0 m)的范围内,温差从0逐渐增大至6.7 ℃。
目前磁浮交通规范对于混凝土梁温差变化的作用是按TB 10092—2017铁路桥涵混凝土结构设计规范的规定进行计算的,对于箱梁,沿箱梁梁高方向的温度变化为:
Ty=T0e-ay
(10)
其中,y为距箱梁顶面的距离,m;T0为箱梁梁高方向的温差,取20 ℃;a为系数,取值5。从图7所示的该公式计算的温度变化曲线与所计算的温度变化对比图可以看出,目前规范与所计算的温度分布还是有一定的差异。在温差最大值方面,所计算值与规范相关不大,但在距顶面的距离超过0.5 m以后,规范温度值要小于计算值,特别是在靠近箱梁底部的0.3 m高度区域,所计算的温度变化与规范差别很大,计算表明在底部区载有一个较大的温差,而规范在远离顶面的底部基本没有温差,这可能导致磁浮轨道梁实际的温度变形大于理论计算值,从而对磁浮车辆的安全运行和线路维护造成不利影响。
4 结论
本文根据上海地区气象资料,采用ANSYS软件对单线磁浮箱形轨道梁在日照作用下的温度特征进行了研究,得到了以下结论:
1) 在日照作用下,混凝土箱梁温度的分布具有明显的非线性和时滞性。箱梁外表面的最高气温可达到50 ℃,外表面的温度变化量要明显大于箱梁内部,箱梁内部达到温度最高值的时间滞后于外表面2 h~4 h。
2)轨道梁截面竖向温差最大值为20.1 ℃,在距顶面0.3 m高度范围内变化显著,并且距底面0.3 m高度范围内也存在明显的温度梯度,在中部的其他区域则温差较小且基本不变。
3)目前磁浮交通规范所采用的温度梯度模型在最大峰值方面相差不大,但在靠近底部的区域有明显的差异。因此,针对单线磁浮箱形轨道梁的温度效应,需进一步进行研究。
