基于PWM作动器的运载火箭伺服系统建模与仿真
2021-10-26梁俊龙呼延霄张贵田尤裕荣
梁俊龙,呼延霄,张贵田,尤裕荣
(1. 西北工业大学燃烧、热结构与内流场重点实验室,西安,710072;2. 西安航天动力研究所,西安,710100)
0 引 言
运载火箭伺服系统接受实时位置调整参数推动火箭发动机喷管以一定速度和方向运动,实现运载火箭推力矢量控制。伺服系统是火箭飞行控制系统中关键的控制执行分系统,如果伺服机构出现故障,将直接宣告发射任务的失败[1]。运载火箭可靠性要求非常高,尤其是载人航天运载火箭,分解到伺服系统上则要求其可靠性至少达到99.9%以上[2]。因此高可靠性的伺服系统是运载火箭的支撑性关键技术,伺服系统优化对提高火箭性能有着重要的影响[3]。
目前成熟的运载火箭多采用传统的机械液压控制系统或基于电液伺服阀的调节系统。在火箭发动机电液伺服系统中,电液伺服阀是用来联接液压部分和电气部分的元件,其功能是把接收到的小功率模拟电信号快速精准的转换为大功率的流量和压力信号,这些信号带动液压缸或者液压马达,从而驱动负载的运动。电液伺服阀充分发挥了电信号传递快、线路连接简单、易于测量和反馈的优点及液压元件具有的响应快、惯性小、输出功率大等优点[4]。文献[5]~[8]对基于电液伺服阀的非对称液压缸伺服系统进行建模仿真,并设计了H∞等控制器,研究了泄漏量对控制系统的影响。
考虑到电压伺服阀控制元部件的批量及规格化生产,降低成本或开发简易廉价的各种转换元件、数字化元部件以及各种抗污染的产品,仍然是今后液压控制系统设计的课题[9]。
某型发动机在研制过程中,采用了基于PWM(Pulse Width Modulation)作动器代替电液伺服阀对位置进行调节,优势有:a)PWM作动器采用数字量控制代替模量,更符合发动机控制系统的发展趋势;b)PWM作动器抗污染能力强,可以直接利用燃油进行作动,使得系统大大简化;c)PWM作动器在非设计点控制特性较好,可以使用作动燃油对伺服系统进行冷却。但由于PWM作动器频响较低,使得火箭伺服系统稳定性变差,增加了控制系统的设计难度。文献[10]采用4个高速电磁阀对双向液压缸的方向和位置进行了控制,并设计了模糊控制器,并进行了试验验证,取得较好的效果。文献[11]对基于高速阀控制的小作动筒工作稳定性研究,并设计了PID控制器,研究了产品的物理参数在不同变化下对稳定性控制的影响。
本文基于PWM作动器伺服系统工作特点,建立了基于传递函数的数学模型,设计了抗积分饱和PID控制器,并采用Matlab/Simulink进行了数学仿真验证,分析了伺服系统稳定性和稳态调节精度。采用AMESim对整个非线性控制系统进行了仿真验证,最后通过地面试验验证了控制算法的可行性。
1 基于PWM作动器工作原理
目前位置伺服系统应用较为广泛的是喷嘴挡板式电液伺服阀,结构原理如图1所示。

图1 喷嘴挡板式电液伺服阀结构原理Fig.1 Double Nozzle Flapper Electro-hydraulic Servo Valves
喷嘴挡板式电液伺服阀一般包括力矩马达和喷嘴挡板阀两部分。当输入控制电流时,力矩马达的衔铁组件产生磁场,并与上磁体和下磁体的电磁铁磁场发生作用,衔铁组件发生偏转,使与衔铁组件刚性连接的挡板偏离中立位置,导致两个喷嘴容腔内的压力发生变化,产生压差从而驱动执行机构。当控制电流的大小和方向改变时,电液伺服阀输出流量的大小和方向或者负载压力的大小也发生改变,从而使执行机构的运动速度和运动方向或者输出力大小也发生改变。
电液伺服作动器结构原理见图2,主要由滑阀、减压阀、PWM高速电磁阀、占空比调整阀、节流器及线位移传感器等组成,其工作原理为:综合控制器根据线位移传感器反馈电压信号,通过控制算法控制驱动高速电磁阀占空比来实现对滑阀位置的闭环控制;同时,减压阀阀芯感受控制油路前后压差,将入口压力减至额定值,保证控制油路压差恒定,为高速电磁阀驱动滑阀运动及其位置的精确、稳定控制提供保证。

图2 PWM作动器原理Fig.2 PWM Actuator Schematic
与电液伺服阀相比,PWM作动器最大的特点是采用减压阀、高速电磁阀等代替了力矩马达和喷嘴挡板机构,提高了系统抗污染能力,并由传统的模拟量控制变为数字式控制方式,用闭环控制的方式实现了滑阀位移的精确控制。
2 位置伺服系统模型
2.1 PWM作动器模型
PWM作动器空载输出流量与输入占空比信号可以用二阶模型表示:
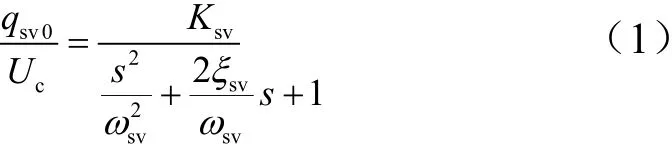
式中Ksv为空载增益;s为拉氏变换因子;svω为作动器自然频率;svξ为作动器阻尼比。设PWM作动器入口为ps,出口为0,无杆腔压力为p1,有杆腔压力为p2。PWM作动器负载压力为

式中n为有杆腔和无杆腔面积比,由于作动筒活塞面积的非对称性,有n=A2/A1;A1为有杆腔面积;A2为无杆腔面积。
PWM作动器两作动窗口的流量为

式中Cd为节流窗口流量系数;w为节流窗口宽度;xsv为阀芯位移;ρ为介质密度。根据式(3)可得:

对式(4)进行求导可得:

定义PWM作动器负载流量为

则作动器流量可写为

式中Kc为PWM作动器流量压力增益系数。
2.2 作动筒模型
以无杆腔流入燃油为例,建立作动筒模型。假设活塞运动方向由无杆腔到有杆腔为正,则作动筒无杆腔和有杆腔的体积可以表示为

式中V01为无杆腔初始体积;V02为有杆腔初始体积;y为作动筒活塞位移。则作动筒初始位置的体积假设作动筒两腔初始容积相等,则有。设Q1为流入无杆腔的流量,Q2为流出无杆腔流量,活塞向正方向移动时(y增大),无杆腔流量增大,有杆腔流量减小,则根据流量连续方程有:
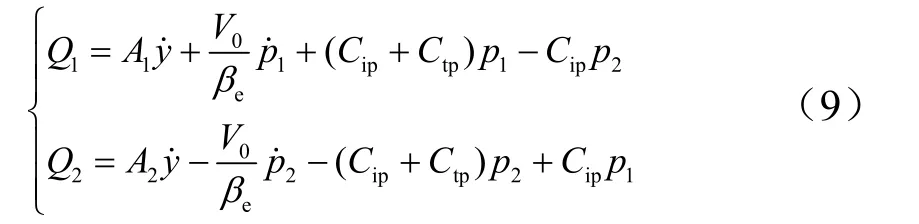
式中Cip为内泄漏系数;Ctp为外泄漏系数。则根据负载流量定义,将式(7)和式(8)代入式(9)可得:
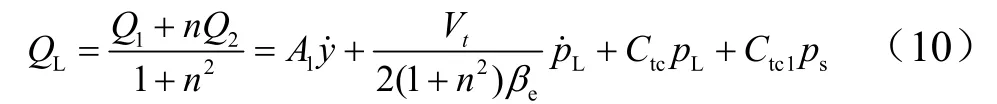
式中Ctc为y﹥0时的总内泄漏系数;Ctc1为总外泄漏系数。其具体表达式如下:

将式(8)代入式(10),有:

式中Kcel为流量压力系数,Kcel=Ctc+Kc。
作动筒和负载的力平衡方程为

式中K为负载弹簧刚度;LF为活塞负载力;m为活塞质量;B为活塞粘性阻尼系数。
2.3 系统传递函数推导
忽略弹簧负载,对式(12)和式(13)取拉氏变换可得:

将上式合并后可得:
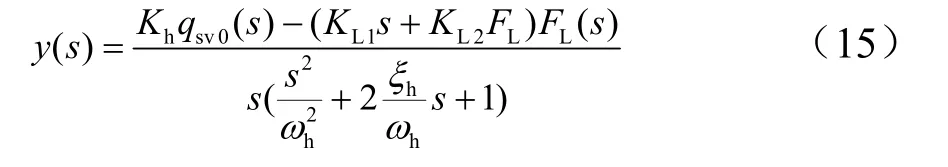
其中:

根据上述推导,将作动筒的冷却流量作为干扰项,则可以得到系统传递函数如图3所示。
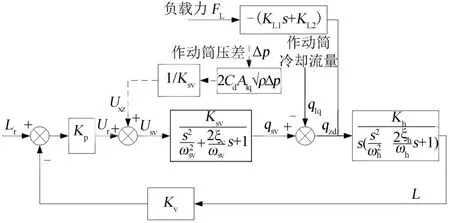
图3 系统传递函数Fig.3 System Transfer Function
3 位置伺服系统稳定性分析
3.1 PWM作动器工作特性
压力特性是负载流量为零时,负载压力与阀芯位移之间的变化关系。
PWM作动器压力特性如图4所示,伺服阀的压力增益通常取最大负载压降的±40%内的平均斜率,该PWM作动器最大负载压降为12.94 MPa,则压力增益取±5.18 MPa内的平均斜率为73.2 MPa/mm。
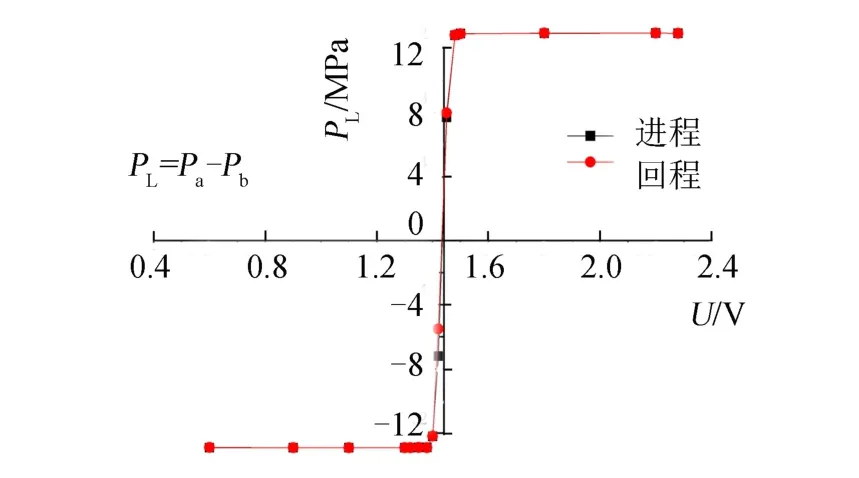
图4 PWM作动器压力特性Fig.4 PWM Actuator Pressure Characteristics
内泄漏特性指负载流量为零时,从回油口流出的总流量。内泄漏量随阀芯位移变化的试验结果见图5,当阀芯处于零位时,内泄漏量最大为0.127 kg/s,随着阀芯位移的增大或减小,泄漏量逐渐减小;当位移大于+0.5 mm或小于-0.5 mm,内泄漏量基本上为零。

图5 PWM作动器内泄漏特性Fig.5 Leakage Characteristics in PWM Actuator
空载流量特性是指负载压降为零时,负载流量与阀芯位移之间的变化关系见图6,其中在±0.5 mm的负重叠区内的流量增益为0.38 (kg·s-1)/mm,在其它区域内的流量增益为0.195 (kg·s-1)/mm,恰好约为负重叠区域内的一半。

图6 PWM作动器空载流量特性Fig.6 No Load Flow Characteristics of PWM Actuator
负载流量特性是指在滑阀阀芯在某一位置开度下,负载压降与负载流量之间的变化关系,它全面描述了PWM作动器的静态性能特性。阀芯在最大位移下的负载流量特性曲线可以表示该作动器工作能力和规格,当负载所需的压力和流量能够被阀芯在最大位移时的负载流量曲线所包围时,PWM作动器就能满足负载的要求。PWM作动器负载流量特性见图7。由最大位移下的负载流量特性曲线可得,流量为0.22 kg/s时对应输出负载压力为12.1 MPa。
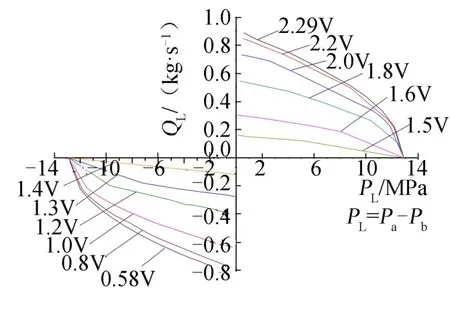
图7 PWM作动器负载流量特性Fig.7 Load Flow Characteristics of PWM Actuator
3.2 控制系统原理框图
图8给出了基于PWM作动器的火箭伺服系统原理框图。通过测量得到的作动筒位移与当前位移指令求差,然后经过抗积分饱和PID控制算法形成PWM作动器占空比信号,来控制PWM作动器滑阀位置,从而改变PWM作动器A、B两控制腔压力和流量,达到控制作动筒位移的目的。
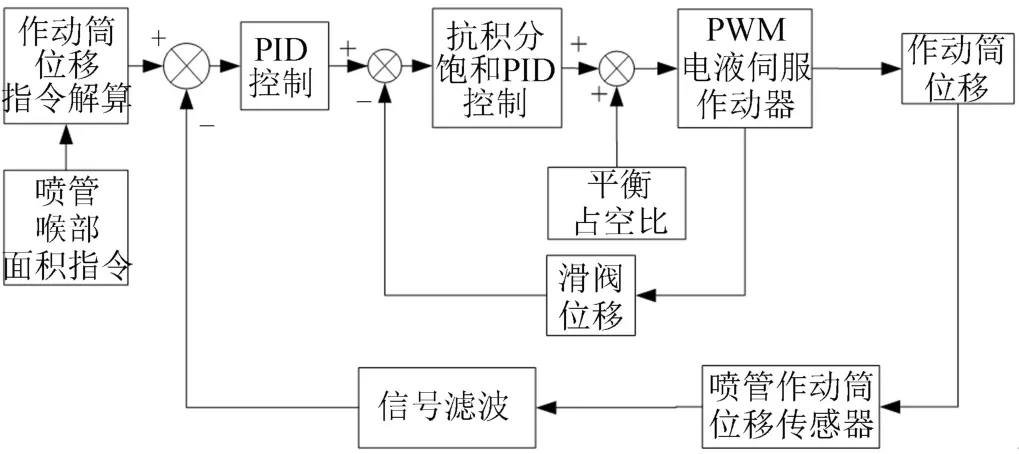
图8 基于PWM作动器的火箭伺服系统原理框图Fig.8 System Principle Block Diagram of Launch Vehicle Servo System based on PWM Actuator
3.3 系统稳态误差分析
在不考虑冷却流量时,假设输入为阶跃信号时,控制系统在负载力作用下的系统误差为
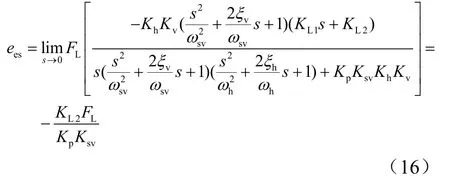
将冷却流量考虑为干扰信号,则其产生的系统误差为

为了减小系统误差,可以引入积分系数,若将冷却流量考虑为干扰信号,则其产生的系统误差为0。
可见,增加积分后,系统稳态误差重新变为0。但是上述算法将冷却流量作为阶跃信号来处理,而实际上冷却流量与压差相关,为时间的函数,所以积分的效果可能达不到理想的效果,为了消除冷却流量带来的影响,可以采用改进后的抗积分饱和控制算法。必要时,通过测量作动筒压差,对PWM作动器的电液进行修正。则在修正指令和冷却流量同时作用下的系统稳态误差为

则使得系统稳态误差为0的PWM作动器电压修正指令为

但实际中伺服系统作动筒的冷却流量可能不能简单得用流量公式计算,此时必须根据不同负载力的大小然后调整电压修正值,使得作动筒位移控制误差满足要求。通过记录不同负载力情况下作动筒压差与修正电压,从而获得二者的拟合关系式。
3.4 系统稳定性分析
为了验证系统的稳定性,则对系统传递函数具体化,可以得到系统开环传递函数为
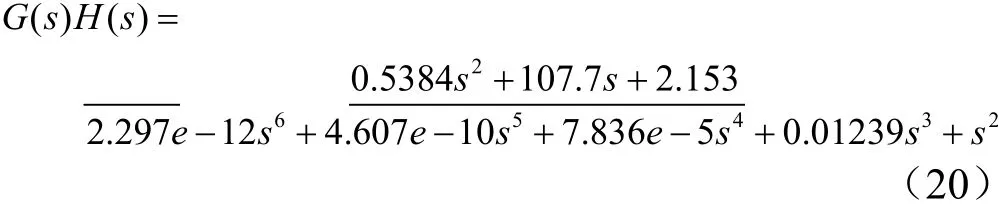
可得到系统幅频特性如图9所示。系统幅值稳定裕度为Gm=7 dB,相位稳定裕度为Pm=38°,相角交界频率为Wg=245 Hz,截止频率为Wp=97 Hz。一般在工程设计中相角裕度一般为30~60°,幅值稳定裕度为6 dB。可见,系统稳定,满足要求。

图9 伺服系统幅值和相位稳定裕度Fig.9 Servo System Amplitude and Phase Stability Margin
4 基于AMESim的数值仿真
为了验证基于PWM作动器的位置系统系统控制特性,采用AMESim软件对其进行了仿真建模,如图10所示,仿真结果如图11至图14所示。仿真模型采用的电机模型为直流电机模型,泵后压力波动对转速的控制影响较小,转速控制较为平稳。仿真过程中对作动机构进行了简化,认为作动筒所受负载力同步。而对于真实的位置伺服系统而言,由于作动筒不同步,导致单个作动筒所受负载力不同。而且由于不同步带来的同步环摩擦力增大,对于动摩擦力而言,可以看作为负载力的增大,影响只是系统最大负载能力。仿真过程作动筒冷却孔按照固定节流孔处理,与实际系统作动筒冷却孔的流量特性有所区别,所以稳态时PWM作动器的平衡位置会略有差别,从而影响系统的闭环控制精度。
图10 AMESim的仿真模型Fig.10 Simulation Model of the AMEsim

图11 作动筒位移仿真结果Fig.11 Action Cylinde Displacement Simulation Results
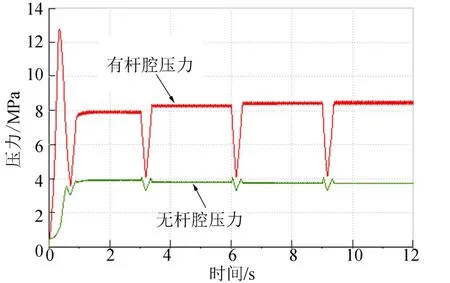
图14 作动筒压力仿真结果Fig.14 Action Cylinder Pressure Simulation Results

图12 柱塞泵后压力和流量仿真结果Fig.12 Simulation Results of Pressure Flow after Plunger Pump

图13 PWM作动器滑阀位移仿真结果Fig.13 Simulation Results of PWM Actuator Spool Displacement
通过仿真结果可以看出,在指令为阶跃响应时,作动筒位移和滑阀位移的稳态误差<±3%,调节时间为0.3 s,满足系统要求。柱塞泵后压力、作动筒有杆腔和无杆腔压力满足设计要求。
5 位置伺服系统系统地面试验验证
从图15位置伺服系统地面试验结果来看,方波指令下,作动筒位置的动态特性和稳定性与仿真结果一致,但位置控制存在一定的稳态误差。
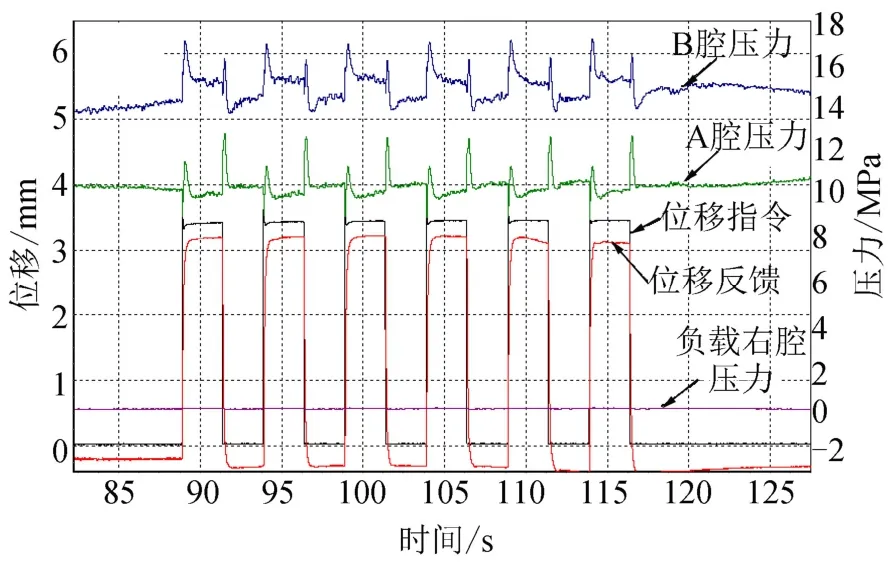
图15 方波指令火箭伺服系统调节特性Fig.15 Regulation Characteristics of Rocket Servo System under Square Wave Command
稳态误差产生的主要原因是试验中冷却流量与仿真结果有一定的差别,导致冷却流量修正模型与仿真模型不一致,从而存在稳态误差。根据地面试验结果对冷却流量模型重新修正后,图16给出了正弦指令下位置伺服系统的跟随特性,可以看出冷却流量模型修正后,稳态误差减小,满足伺服系统位置控制稳态误差<±3%的要求。
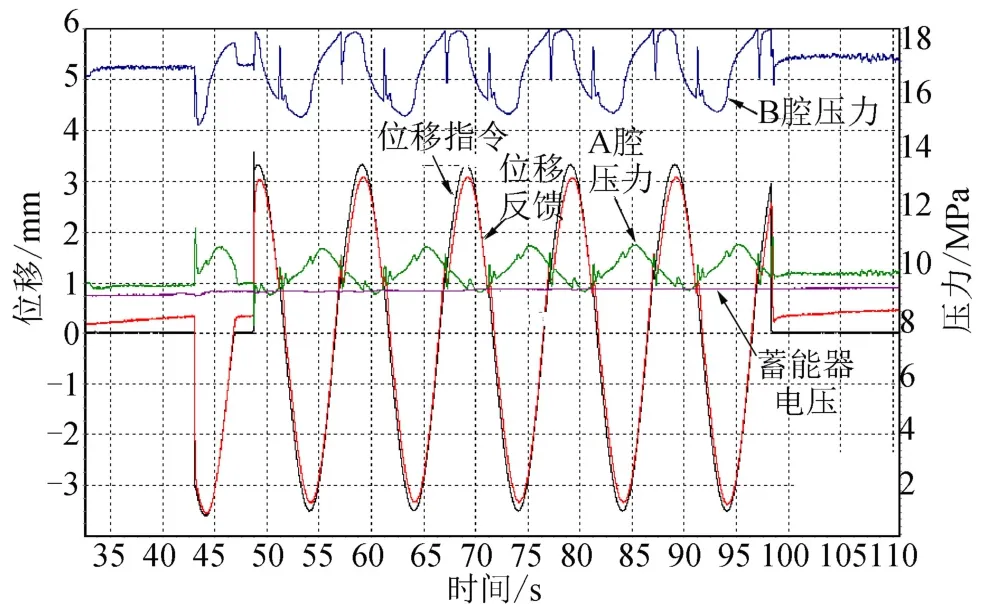
图16 正弦指令火箭伺服系统调节特性Fig.16 Regulation Characteristics of Rocket Servo System under Sinusoidal Command
6 结束语
本文根据运载火箭伺服系统工作特点,完成基于PWM作动器的火箭发动机位置伺服系统建模,获得了控制系统传递函数,设计了抗积分饱和PID控制器,对系统稳定性和稳态误差进行了分析,并采用AMESim软件对非线性系统进行了仿真验证。最后通过位置伺服系统地面试验验证了控制算法和调节方案的可行性。
仿真结果表明,基于PWM的火箭伺服系统稳态控制精度和动态响应特性满足设计要求,为运载火箭伺服系统提供了一种新的设计思路。
