基于R/S分析法的矿井涌水量时间序列分析及定量预测*
2021-10-25田罡豪崔中良胡体才黄保胜夏荣辉刘红伟任周洪
田罡豪,崔中良,胡体才,黄保胜,夏荣辉,刘红伟,王 宏,任周洪
(云南驰宏锌锗股份有限公司,云南 曲靖 655000)
0 引言
R/S分析法是现代非线性理论的重要组成部分[1],目前被广泛应用于自然科学领域的时间序列研究。王波雷等[2]、冯新灵等[3]认为R/S分析法是进行气候预报的有效手段,并运用R/S分析法研究了气候变化趋势。乔美英等[4]基于R/S分析法对千秋煤矿矿井的涌水量进行了分形特性研究,结果表明R/S分析法可用于涌水量时间序列研究,这为矿井涌水研究与治理提供了新的思路。基于R/S分析法开展矿井涌水量预测所需水文地质信息极少,因此在水文地质条件不明或水文地质条件研究程度较低的情况下具有较大的应用潜力。然而R/S分析法目前仅能实现定性预测,除少数学者尝试定量研究外[5-8],基于分形刻画特征的涌水量定量预测研究还鲜有报道,因此本文采用R/S分析法实现对矿井涌水量时间序列的分形刻画,并结合灰色预测理论实现矿井涌水量的定量预测,以期为更深入地开展分形预测打好基础。
1 分析法概述
1.1 R/S分析法基本原理
R/S分析又称变标度极差分析(重标极差法),最初由HURST于1965年提出,后经MANDELBROT和WALLIS不断完善而成熟[1-3]。R/S分析法的基本思想是通过改变样本序列的时间尺度,研究其在不同尺度范围内的统计规律,从而进行大小时间尺度间的相互转换[9]。R/S分析法的基本步骤叙述如下。
(1)假设不同时间t1,t2,t3,…,tn的矿井涌水量分别为x1,x2,x3,…,xn,那么矿井涌水量时间序列即为{xi,n≥i≥1}。计算在τ(τ≥2)时段内矿井涌水量平均值
(2)在时间tj时,矿井涌水量对于平均值的积偏差为
(3)计算x(t,τ)的极差
R(τ)= maxx(t,τ)- minx(t,τ),
tn≥t≥t1,τ=2,3,4,…。
(4)同一个τ值下,与R(τ)对应的矿井涌水量标准偏差为
(5)极差R(τ)与标准偏差S(τ)的比值为
τ=2,3,4,…。
(6)R(τ)/S(τ)=(τ/2)H+C,τ=2,3,4,…;C为常数。
两边取对数得
(1)
式中,H为Hurst指数,等于以双对数坐标系ln(τ/2)为横轴、ln(R/S)为纵轴中应用最小二乘法拟合得到的直线斜率。Hurst指数可以表征时间序列的随机性[9-12]:①当0.5>H>0时,表示反持续性时间序列,为负反馈机制,意味着未来的趋势与过去相反,H值越接近0,反持久性越强;②当H=0.5时,表示随机性时间序列,即未来时间序列的变化与过去时间序列没有关系;③当H>0.5时,表示持续性时间序列,具有长期记忆性,且其记忆性不随时间标度的变化而变化,意味着未来与过去呈现相同的变化趋势,H值越大,持久性越强。
非线性动力系统具有非周期循环特征,平均循环周期的确定常借助时间序列V(τ)-lnτ关系图进行分析,统计量V(τ)的计算公式为
1.2 灰色预测模型
信息完全确定的系统为白色系统,信息完全未确定的系统为黑色系统,而灰色系统介于两者之间,既含有已知信息又含有未知信息。矿井涌水量预测与水文地质条件、开采体积、开采强度等多种因素有关,既有已知信息,又有未知信息,是一个典型的灰色系统[7]。灰色预测模型是针对灰色系统的特点而建立的预测模型,所需建模信息少,运算方便,是处理小样本预测问题的有效工具。其中GM(1,1)是最常用的灰色预测模型,具体计算步骤如下。
(1)根据涌水量原始数据序列X(0)计算一次累加序列X(1)。
设X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)},则
(2)建立矩阵B,Y。
(3)求发展灰数a及灰色作用量b。
GM(1,1)模型的影子方程为

(4)确定GM(1,1)模型。
将求得的参数a、b代入GM(1,1)模型的时间响应方程得
则原始涌水量时间序列预测模型为
k=1,2,…,n。
1.3 R/S灰色预测模型
R/S灰色预测模型的建立分为4个步骤:
a.运用R/S分析法刻画涌水量时间序列分形特征(Hurst指数、平均循环周期T);
b.选取长度为T-1的涌水量时间序列{x1,x2,x3,…,xT-1}建立灰色预测模型GM(1,1)1;
c.对建立的灰色预测模型进行精度检验,若建模精度大于80%,开展下一步;若建模精度小于80%,进行修正后开展下一步。
d.有两种预测模式:①基于灰色预测模型GM(1,1)1预测xT。基于涌水量时间序列{x2,x3,x4,…,xT}建立灰色预测模型GM(1,1)2预测xT+1。重复此步骤可预测今后若干时间序列的涌水量。②Hurst指数若显著大于0.5,则说明时间序列具有长程相关性,并且持续性极强,此时循环周期远大于平均循环周期,因此可用灰色预测模型GM(1,1)1连续预测xT、xT+1、xT+2等。
2 研究区涌水量时间序列
研究区含水层类型为岩溶裂隙含水层,整体富水性弱至中等。其中矿床直接充水含水层由石炭系威宁组、摆佐组、大塘组及泥盆系宰格组组成,矿床顶板间接充水含水层由二叠系栖霞-茅口组组成,矿床底板间接充水含水层由震旦系灯影组组成。矿床直接顶板隔水层由二叠系梁山组及石炭系马平组组成,矿床直接底板隔水层由泥盆系海口组及寒武系筇竹寺组组成,目前隔水性能较好。根据研究区2011-2017年季度涌水量时间序列(见图1)可以看出,2015年一季度至2017年四季度,涌水量整体呈小幅波动式增长。
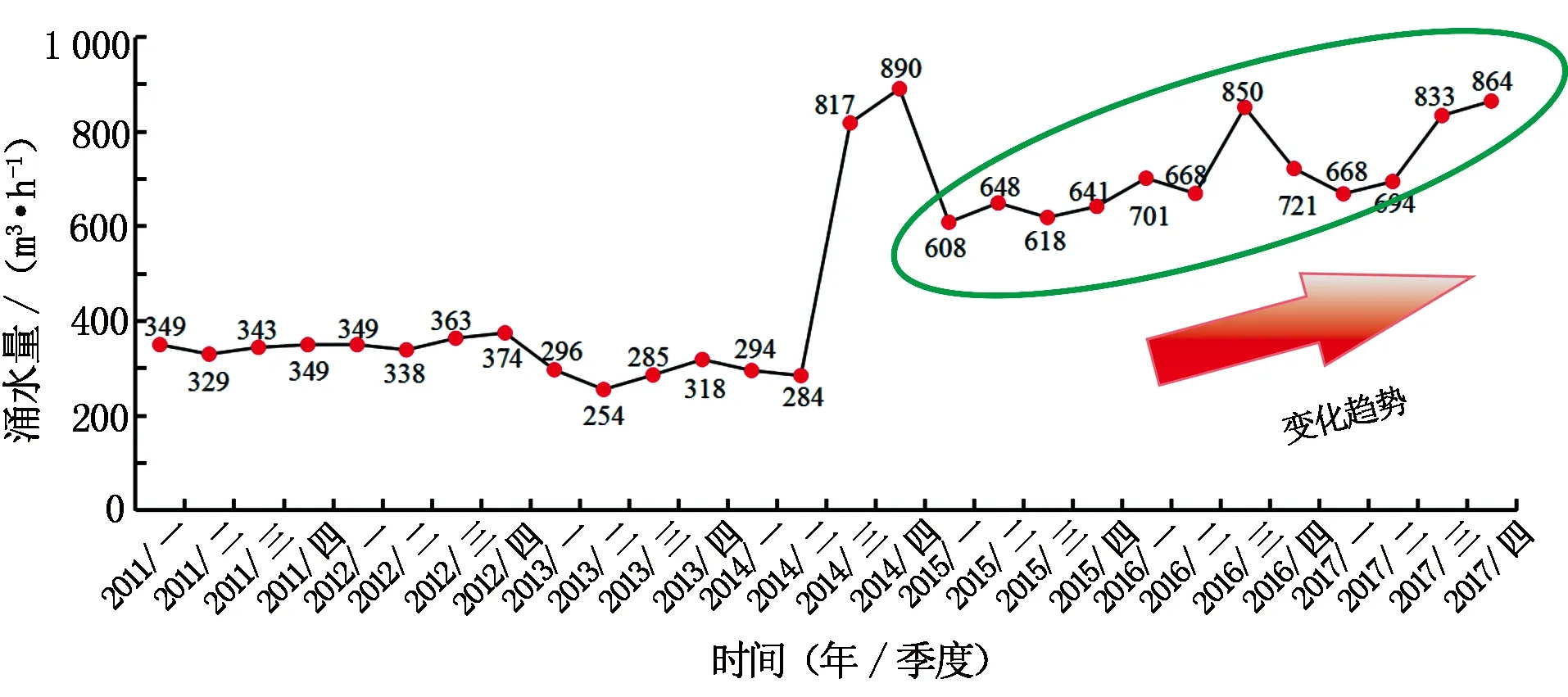
图1 矿井2011-2017年季度涌水量时间序列
3 涌水量时间序列的R/S分析
3.1 涌水量时间序列的Hurst指数
计算2011-2017年季度涌水量时间序列的分析参数(见表1),在双对数坐标系中拟合得到季度涌水量时间序列ln(R/S)-ln(τ/2)线性关系图(见图2)。由图2可知,相关系数大于0.98,判定系数接近1,说明模型拟合度较高,拟合效果较好。拟合直线的斜率为1.027 2,即Hurst指数估计值为1.027 2,与1极为接近,说明时间序列具有长程相关性,并且持续性极强。2011-2017年季度涌水量变化曲线前一部分呈低数值平坦形(略有波动),后一部分为剧烈抬升后的波动增长形(见图1),根据Hurst指数预测2018年季度涌水量相对于2017年整体应呈增大趋势,但不排除小范围的波动。

表1 矿井涌水量时间序列R/S分析结果

图2 涌水时间序列ln(R/S)-ln(τ/2)线性关系图
3.2 涌水量时间序列平均循环周期
矿井涌水量时间序列具有非线性分形特征,而非线性动力系统的特征之一便是具有非周期循环特征。在矿井涌水量时间序列分析中,常引入统计循环概念,即平均循环周期,平均循环周期的确定可以借助时间序列V(τ)-lnτ关系图分析得到。根据V(τ)、lnτ值绘制时间序列V(τ)-lnτ关系图(见图3)。V(τ)单调性变化分界点也是时间序列持续性的消失点,因此找出V(τ)-lnτ关系曲线的第一个转折点,也就找到了时间序列的平均循环周期。由图3可知,转折点τ=5,说明研究区矿井涌水量时间序列的平均循环周期为5个季度。

图3 涌水量时间序列V(τ)-lnτ关系图
3.3 涌水量时间序列的随机性
Hurst指数是表征时间序列随机程度的重要参数。上述计算及分析结果均表明研究区矿井涌水量时间序列为有偏随机游走,即历史涌水量时间序列与未来涌水量时间序列有相关性,随机打乱原始矿井涌水量时间序列,根据重新计算的Hurst指数,可以有效评估Hurst指数估计量的有效性。若原始涌水量时间序列真正独立,为完全随机序列,则打乱后重新计算得到的Hurst指数保持不变。若重新计算得到的Hurst指数发生变化,则说明原始的矿井涌水量时间序列存在记忆性,亦说明了利用Hurst指数开展分析预测的有效性。将2011-2017年季度涌水量时间序列打乱,重新计算得到的Hurst指数为0.936 9(见图4),发生了较明显的变化,说明原始的矿井涌水量时间序列存在记忆性,为有偏布朗运动。
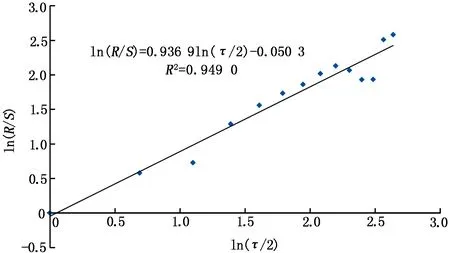
图4 重新构建涌水量时间序列的ln(R/S)-ln(τ/2)线性关系图
4 涌水量时间序列预测模型
4.1 灰色预测模型构建
基于2011-2017年季度涌水量数据建立灰色预测模型GM(1,1),该模型的时间响应方程为x(1)(k+1)=6 749.66e0.042 4k-6 400.68,则原始涌水量时间序列预测模型为x(0)(k+1)=(1-e-0.042 4)6 749.66e0.042 4k。根据原始涌水量时间序列预测模型预测2011-2017年季度涌水量,并进行误差分析(见表2、图5)。

表2 灰色预测模型GM(1,1)建模误差分析

图5 GM(1,1)模型预测2011-2017年涌水量时间序列
从表2、图5可以看出:GM(1,1)模型预测的相对误差为0.01%~71.41%,平均相对误差为18.65%,模型建模精度为81.35%;GM(1,1)模型在涌水量序列剧烈变化时的相对误差急剧增大,说明模型精度急剧下降。
4.2 R/S灰色预测模型构建
研究区矿井涌水量时间序列的平均循环周期为5个季度,因此连续选取4个季度涌水量建立灰色预测模型。选取2017年4个季度涌水量建立灰色预测模型GM(1,1),该模型的时间响应方程为x(1)(k+1)=6 515.03e0.104 1k-5 847.36,则原始涌水量时间序列预测模型为x(0)(k+1)=(1-e-0.104 1)6 515.03e0.104 1k。R/S灰色预测模型GM(1,1)预测的相对误差为0%~4.78%,平均相对误差为2.44%,模型建模精度为97.56%。

表3 R/S灰色预测模型GM(1,1)建模误差分析结果
4.3 预测模型精度对比
应用两种预测模型预测2018年季度涌水量时间序列,结果见表4。由表4可知:灰色预测模型GM(1,1)预测结果的绝对误差为130.82~262.20,相对误差为11.14%~21.48%,平均相对误差为18.24%,预测精度为81.76%;R/S灰色预测模型GM(1,1)预测结果的绝对误差为32.95~189.11,相对误差为2.67%~16.22%,平均相对误差为10.94%,预测精度为89.06%。R/S灰色预测模型是基于刻画涌水量时间序列平均循环周期上的灰色预测模型,可有效减少预测样本数量,一定程度上确保了涌水量时间序列的平稳性,因此预测精度高于灰色预测模型。综上所述,R/S灰色预测模型兼具灰色预测及R/S分析的特点,相比R/S分析法能实现定量预测,相比灰色预测能提高预测精度,可满足矿井防治水要求。

表4 两种预测方法的结果对比
5 结论
a.2011-2017年季度涌水量时间序列的Hurst指数估计值与1极为接近,说明时间序列具有长程相关性,并且持续性极强。
b.Hurst指数有效性的验证结果表明,研究区原始的矿井涌水量时间序列存在记忆性,为有偏布朗运动。为量化矿井涌水量时间序列的记忆性,计算得出研究区矿井涌水量时间序列的平均循环周期为5个季度。
c.基于2011-2017年季度涌水量数据建立的灰色预测模型、R/S灰色预测模型建模精度分别为81.35%、97.56%,对2018年季度涌水量时间序列的预测精度分别为81.76%、89.06%。
d.R/S灰色预测模型兼具灰色预测及R/S分析的特点,相比R/S分析法能实现定量预测,相比灰色预测法能提高预测精度,在水文地质条件不明或研究程度较低的情况下具有较大的应用潜力。
