老龄化对居民医疗保健消费支出影响研究

□文/邹银花

（首都经济贸易大学统计学院 北京）

［提要］根据最新的第七次人口普查数据显示：我国的老龄化程度在不断的加深。在此背景下，本文基于我国2014～2019年省际面板数据，研究人口老龄化对我国居民人均医疗保健消费支出的影响。为了拓宽模型的适用范围，同时也修正参数型模型偏差较大的问题，在建模时采用非参数贝叶斯密度比回归模型来研究人口老龄化对我国居民人均医疗保健消费支出的影响。结果表明：人口老龄化对人均医疗保健消费支出有显著的正向影响，所以国家相关部门应注意人口老龄化带来的医疗保健需求增加相关问题，积极做出相应措施，健全医疗保障体系。

一、引言

近年来，我国老年人口的人数和比重都在持续上升，根据国际上人口老龄化的划分标准，中国早在2000年就已经进入老龄化社会。根据第六次人口普查数据，2010年我国60岁以上老年人数占总人口的13.9%，而根据最新的第七次人口普查数据，该比例已经提升到了18.7%，以此可以看出人口老龄化程度在不断的加深。而根据国家统计年鉴的相关数据显示，我国居民人均医疗保健消费支出也呈现逐年增长趋势，由2014年的1，045元增长到2019年的1，902元。可以看出，随着老龄化程度的加深，居民人均医疗保健消费支出随之增加。

近年来，老龄化作为当下研究热点之一，国内外的不少学者都围绕此进行了相关的研究。Grossman认为老年人会比年轻人更加倾向于医疗保健消费。Murthy和Ukpolo利用时间序列相关数据，发现了年龄是造成居民医疗保健消费支出的原因之一。张冲等研究了我国农村人口老龄化和农村居民医疗保健消费支出的关系，得出农村老龄化对农村医疗保健消费支出有推动作用的结论。慕欣芸根据2001～2016年省际面板数据利用最小二乘回归方法分析了我国城乡整体人口老龄化对居民医疗保健消费的影响以及城乡间的差异。孟婷等基于1999～2018年安徽省统计数据得出了人口老龄化对城镇居民医疗保健消费支出存在长期的正向促进作用的结论。

上述的文献大都是建立计量模型，而在计量模型中常见的假设是随机效应的分布为正态分布，但是在实际应用中，当省份之间存在较大的差异性时，随机效应的正态性假设便存在一定的不合理性，进而影响模型中参数的估计效果。除此之外，随着经济问题的复杂化，各组数据各自的随机效应也很难用一个简单的参数模型来刻画，因此本文考虑用非参数贝叶斯密度比回归模型对数据进行建模，假设随机效应分布的先验为Dirichlet过程，以为了消除随机效应分布的参数型假设的局限性，同时也可以拓宽模型的适用范围，修正参数型模型偏差较大的问题，并且根据模型参数估计结果，提出合理性建议。

二、数据和变量说明

（一）数据和变量选择。本文研究的是人口老龄化对人均医疗保健消费支出的影响，但是影响医疗保健消费支出的因素很多，如果只考虑了人口老龄化这一单一因素，必然会使很多因素归到残差中。因此，本文基于我国2014～2019年省际面板数据，其中被解释变量居民人均医疗保健支出，解释变量老年人口抚养比、人均可支配收入、医疗保健消费价格指数、城乡居民基本养老保险基金支出数据均来自于2014～2019年《中国统计年鉴》或通过计算得到。本文之所以选择老年人口抚养比来反应我国老龄化程度问题，是因为它是反映人口老龄化导致的社会后果的指标之一。此外，根据现有文献的回顾和分析，我们发现居民的医疗保健消费还可能受人均可支配收入、医疗保健消费价格指数、城乡居民基本养老保险基金支出等因素的影响，因此也需要将这些因素纳入模型之中。

（二）变量说明

1、被解释变量。居民人均医疗保健支出，是指全国人均用于医疗和保健的药品、用品和服务的总费用。包括医疗器具、药品以及医疗服务。

2、核心解释变量。老年人口抚养比，用于衡量省份或地区人口老龄化程度的指标。也称为老年人口抚养系数，指65岁及65岁以上的老年人口数与劳动年龄人口数（15～64岁劳动年龄人口数）之比。

3、控制变量。（1）人均可支配收入，因为收入是消费的函数，所以说消费者的购买力会随着收入的改变而随之改变。（2）医疗保健消费价格指数，反映一定时期内城乡居民所购买的医疗保健消费品和服务项目价格变动趋势和程度的相对数。（3）城乡居民基本养老保险基金支出，指按照国家政策规定的开支范围和开支标准从城乡居民基本养老保险基金中支付给参加城乡居民基本养老保险的个人养老保险待遇支出，以及由于参保人员跨统筹地区或跨制度流动而发生的支出等。

三、密度比回归模型

设i代表省份或者地区，j代表时间，yij表示第i个地区在第j年的人均医疗保健支出，xij，1表示第i个地区在第j年的老年人口抚养比，xij，2表示第i个地区在第j年的人均可支配收入，xij，3表示第i个地区在第j年的医疗保健消费价格指数，xij，4表示第i个地区在第j年的城乡居民基本养老保险基金支出。我们建立如下的回归模型：

Yij=βTXij+εij

设f0是一个预先设定的基准分布，那么每一个省份的密度fi函数可以用下面的密度比模型来表示，

fi（εi|β，θi）＝f0（yij-βTxij）exp（γ0i+θiTq（yij-βTxij））（i=1，…，31；j=1，…，5）

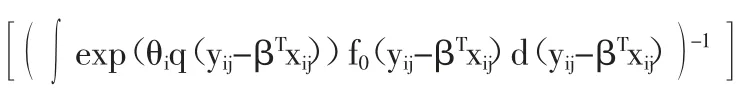
四、模型的贝叶斯推断及结果分析

我们使用贝叶斯方法对模型进行统计推断，设定β1、β2、β3、β4的先验分布均为正态分布N（0，100），选择Ferguson提出的Dirichlet过程作为先验分布，即G～DP（α，G0）。这里也给α一个先验，以产生更大的弹性，选择伽马分布Gamma（1，1）作为其先验分布。Dirichlet过程有多种构造形式，这里选择Sethuraman提出的一种便捷的Dirichlet过程构造方法，称为Stick-breaking构造。假设分布G服从Dirichlet过程DP（α，G0），其中α为集中参数，G0为基准函数。那么，G可以表示为：

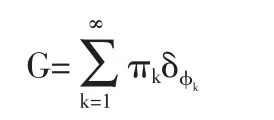
确定各参数的先验分布之后，接下来我们就需要进行后验样本的MCMC抽样，由于涉及到Dirichlet过程且参数较多，使用传统的MCMC抽样算法会降低效率，R语言中有一个Nimble包可以有效的利用C++生成代码并提高效率，所以本文将利用Nimble包对数据进行后验抽样以进行参数估计和相关统计推断。

图1为人均医疗保健支出的核密度曲线图，根据图片可以看出人均医疗保健支出分布呈现出右偏、多峰等特征，这些特征都表明了正态性假设的计量模型经常不够稳健。（图1）

图1 人均医疗保健支出核密度曲线图

在计量模型中，为了减少各个序列数据中出现异方差的结果，通常都会对数据进行一定的预处理，比如取对数。本文的数据在不进行任何预处理时，建立简单的计量模型，得出的均方误差MSE=92909.23，同时根据Breusch－Pagan检验的结果pvalue值为9.57310-4，可知原数据存在一定的异方差性。而本文采用的非参数贝叶斯密度比模型进行建模时，同样也是对数据不进行任何的预处理，得出的均方误差MSE=736.41，说明本模型可以在一定程度上减少异方差带来的误差，而且可以减少对数据进行预处理，以减少预处理带来的相关问题。

表1给出了β的后验均值，后验标准差和95%后验置信区间的上下限。根据系数可以判断出老年人口抚养比、人均可支配收入、医疗保健消费价格指数、城乡居民基本养老保险基金支出四个变量对于人均医疗保健支出都具有正向影响，其中老年人口抚养比每提升1个百分点，人均医疗保健支出增加48.653元；人均可支配收入每提高1元，人均医疗保健支出增加0.015元；医疗保健消费价格指数每提高1个单位，人均医疗保健支出增加1.563元；城乡居民基本养老保险基金支出每提高1元，人均医疗保健支出增加0.004元。（表1）

表1 模型参数估计结果一览表

五、总结及建议

本文基于我国2014～2019年省际面板数据，通过建立一个非参数贝叶斯密度比模型来探究人口老龄化对于人均医疗保健支出的影响效应。选择建立非参数贝叶斯密度比回归模型是因为该模型可以消除随机效应分布的参数型假设的局限性，同时，也可以拓宽模型的适用范围，有效的利用先验和样本信息。根据研究结果表明，人口老龄化对于医疗保健消费支出具有一定的正向影响，也就是说明当人口老龄化加重时，人均医疗保健消费支出会相应的增加，这可能是由于老年人由于患病风险会比年轻人高，因此会增强对医疗保健服务的依赖性，进而拉动医疗保健消费的增长。同时，人均可支配收入、医疗保健消费价格指数、城乡居民基本养老保险基金支出等对于医疗保健支出也都具有正向影响，这些也都与正常的情况相符合。

随着老龄化的逐渐加重，人们对于医疗保健的需求和支出都在加大，随之带来的难题就是国家和政府如何实现健全医疗保障体系，其次就是如何有效的减少老年人常见病对于家庭和个人带来的影响。人口老龄化的加重会增加老年人常见病的费用支出，而科学的宣传和有效的预防可以减少老年人患病的几率。所以，可以将饮食健康和常见病知识宣传融入家庭、社区、街道、专业养老机构等内部。所以，我国相关机构可以加强对老年人的宣传教育，制定定期体检的相关政策，以及做好定期体检的重要性和必要性的宣传工作，努力做到疾病的早发现、早治疗，进而减轻居民的医疗保健支出。