基于应变楔模型的砂土地基水平循环受荷桩简化分析方法
2021-10-25邢康宇吴文兵张凯顺刘浩
邢康宇,吴文兵,张凯顺,刘浩
(1.中国地质大学 工程学院,湖北 武汉 430074;2.岩土钻掘与防护教育部工程研究中心,湖北 武汉 430074;3.中铁工程咨询集团有限公司 郑州设计院,河南 郑州 450001)
0 引言
海上风电机组、钻井平台等海洋工程结构物使用的桩基础在服役期间往往需长期承担由风、波浪、海流带来的周期性循环荷载,相较于静载作用,桩基础受到水平循环荷载作用时其承载力、侧向位移刚度将出现不同程度下降,导致桩身位移过大,极易引起上部建筑物安全问题。造成这一现象的本质原因是循环荷载引起的土体塑性应变累积,使桩侧土体刚度等工程性质产生弱化。目前分析水平循环受荷桩工作性状较为普遍的理论计算方法是p-y曲线法,最初由H.Matlock[1]、L.C.Reese等[2]提出,将静力p-y曲线法中的极限土抗力进行折减,从而考虑桩侧土的弱化,已纳入API等设计规范中,随后许多学者[3-4]在此基础上进一步提出了不同的折减方法。p-y曲线法形式较为简单,工程实际中应用方便,但大多依据小循环次数作用下的桩基荷载试验提出,无法直接考虑荷载作用次数和荷载幅值的影响。已有研究[5]表明,p-y曲线法的计算结果可能存在较大误差,并不适用于长期循环荷载作用下的桩基响应计算。M.Achmus[6]、胡安峰等[7]基于室内循环三轴试验结果建立的砂土刚度弱化模型[8]考虑桩侧土的循环弱化特性,并将其嵌入到三维有限元数值模拟中计算得到桩身位移响应,可直接考虑循环荷载次数和荷载幅值的影响。水平荷载作用下桩侧土应力和应变水平随地基深度和荷载大小发生变化[9-10],因此不同埋深处土体循环弱化程度也不同。与p-y曲线法相比,有限元法优势在于可以确定桩侧土体的应力分布规律,然后根据刚度弱化模型,确定不同深度桩侧土的弱化程度,进而分析桩身的水平位移响应,但其计算过程较为复杂,不利于工程应用。因此,建立能有效反映桩侧土循环弱化特性并便于工程应用的水平循环受荷桩简化分析方法有着重要的工程意义。
M.Ashour等[11]建立的应变楔模型结合三维桩-土相互作用确定桩基水平静力响应,可充分考虑宏观土抗力-桩身位移与微观上土体应力-应变的联系,并确定桩侧土应力、应变分布;在此基础上,K.Lesny等[12]考虑桩侧土的循环累积塑性应变,通过对应变楔模型[11]中的参数ε50进行修正以考虑循环荷载的影响,但累积塑性应变计算方法并未考虑应力幅值等特性对砂土循环弱化特性的影响;杨晓峰等[13]指出,现有应变楔模型桩身位移线性变化位移假设会造成一些问题和矛盾,并基于此建立了改进的静力应变楔模型。
针对上述问题,在前人研究基础上,本文基于应变楔模型计算水平荷载作用下桩侧土的应力分布规律,然后由砂土刚度衰减经验公式确定桩侧土的循环弱化程度,对静力应变楔模型中的应力应变关系进行修正以考虑循环荷载的影响,建立计算水平循环受荷桩侧向位移的简化分析方法,最后通过算例分析验证本文方法的有效性与合理性。
1 基于应变楔模型的简化分析方法
1.1 应变楔模型
如图1所示,在应变楔模型中,桩前被动受压土体被简化为三维楔形体[11],其几何大小与桩基受荷水平相关,在桩基达到极限承载能力前,荷载大小变化会引起桩前土体应力-应变水平的改变,进而导致楔形体宽度、深度的动态变化。M.Ashour等[11]假设极限承载状态下楔形体的底角β为静三轴试验中土体破坏面的方向夹角。则在达到极限承载状态前的任一载荷作用下,动态楔形体的几何参数由式(1)~(2)确定[11]:
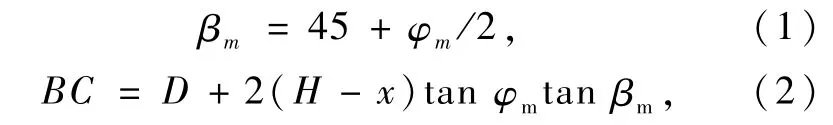
式中:βm为三维楔形体动态底角;φm为土体内摩擦角发挥值;BC为地基深度z处楔形体前置宽度;D为桩径;H为当前被动楔形体深度,与桩身侧向位移的第一零点深度Z0有关,具体取值为弹性长桩H=0.69Z0,中长桩H=(0.69~1)Z0,刚性桩H=Z0。
如图1所示,对于深度z处的应变楔水平截面有

图1 应变楔模型基本形状Fig.1 Basic shape of strain wedge model

式中:Δσh=σh-K0σ′v,为桩侧楔形体的水平增应力,考虑成桩效应,K0=1,则Δσh相当于三轴试验的偏应力σ1-σ3(水平应力σh为轴向应力σ1,竖向有效应力σv′相当于围压σ1);p为单位桩长上作用的桩侧土反力;τ=2′σvtanφm,τf=σvtanφ,τ≤τf,τ为桩侧土体剪应力,其中φ为土体峰值内摩擦角;S1和S2为桩截面形状因子,圆形桩分别取0.75和0.5,方形桩均取1。
杨晓峰等[13]指出,现有应变楔模型[11]假设桩前楔体范围内桩身位移呈线性变化,与实际桩身位移非线性变化的情况有所出入,会对计算结果造成一定误差,并采用非线性位移假设对其进行修正。在此基础上,本文假设桩身位移在楔体范围内呈非线性变化,并引入邓肯-张模型[14]描述土体应力-应变状态,以便后文考虑土体循环弱化特性,对应变楔模型进行改进,如图2所示。为计算方便,结合有限差分法,将桩体与楔形体进行均匀离散,离散长度为h,埋深段桩长为L,其范围内桩体与土体离散层数为mL=L/h,楔形体内桩体及土层离散层数为mH=H/h。依据差分原理、邓肯-张模型及土体应变莫尔圆原理[11],任一荷载作用下楔内离散点i处桩身位移yi、桩段i的转角δi,与对应土层i的摩擦角发挥值φmi、水平增应力Δσhi、应变εi的关系分别为
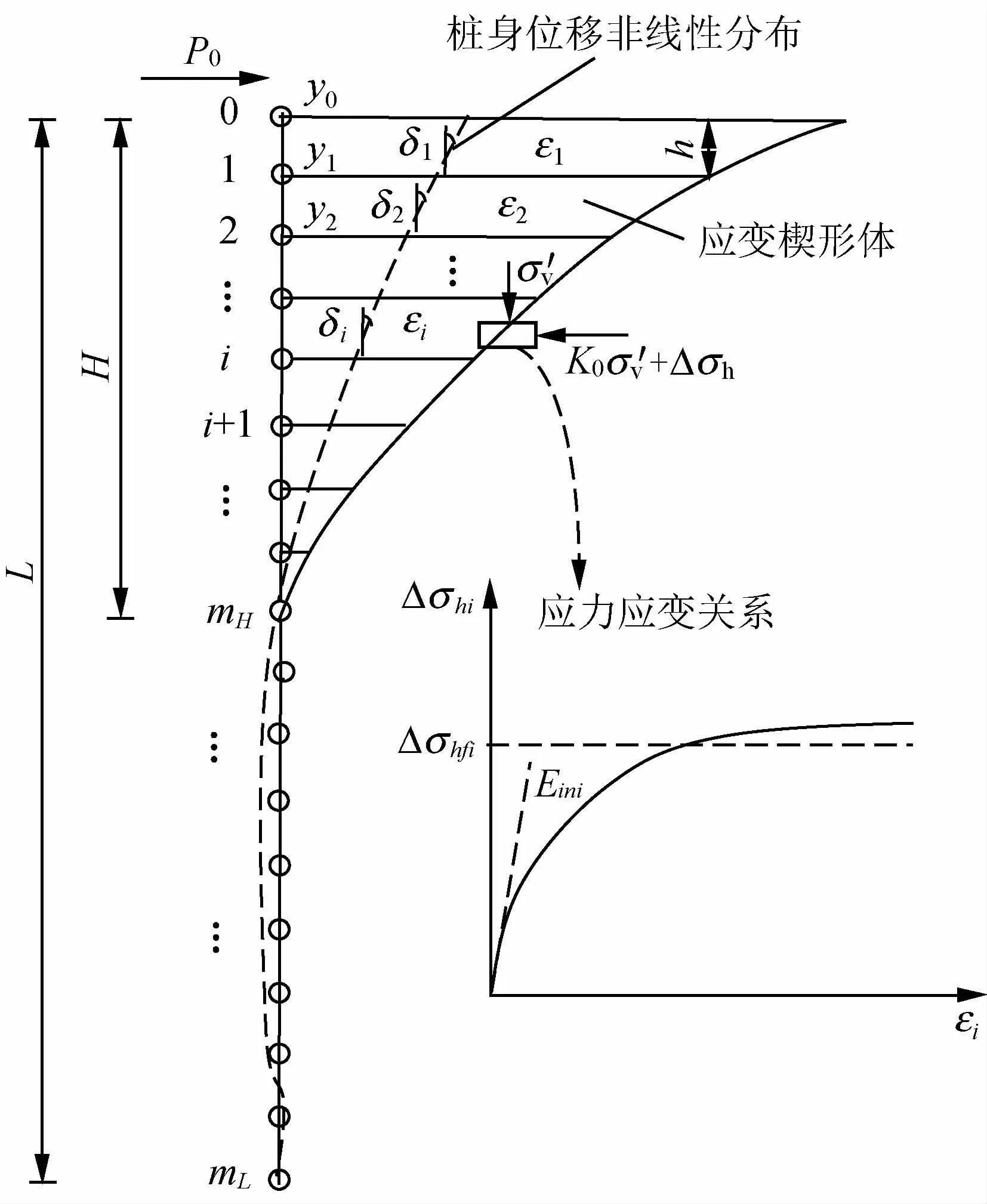
图2 改进的应变楔模型及桩身差分化[13]Fig.2 Modified SW model and discretion of pile[13]

式中:νi为土体泊松比;Eini为初始加载模量,Eini=KePa(σ′vi/Pa)n;Pa=101 kPa,为标准大气压;Ke,n,Rf为计算参数,与砂土密实度有关[15];Δσhfi为极限水平应力增量,对应于三轴试验静偏应力破坏强度σsfi,计算式为

根据土体应力发挥水平,内摩擦角发挥值φmi可由式(7)确定,
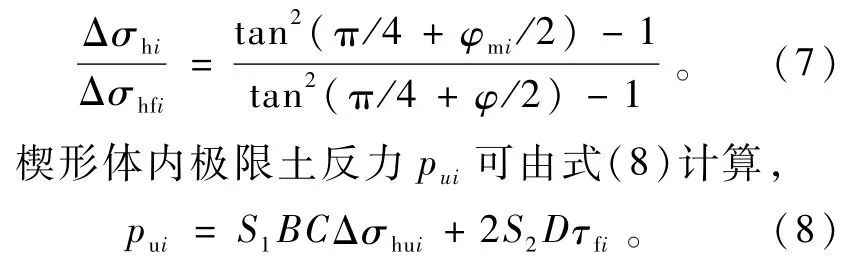
利用改进应变楔模型求解桩身静力水平荷载响应的流程图如图3所示,据此可以确定水平荷载P0作用下不同埋深处桩侧土的应力应变水平。求解过程需结合弹性地基梁法进行迭代求解,水平荷载作用下桩段i的挠曲方程为

式中:EI为桩身抗弯刚度;ki为地基反力模量。对于弹性长桩,楔形体内ki=2pi/(yi-1+yi),楔形体以下区域ki=ηhzi,其中ηh为地基反力系数,其取值可参考文献[16]。
根据差分式与微分式的关系,可将各桩身所有离散桩段的式(9)转化为差分方程组
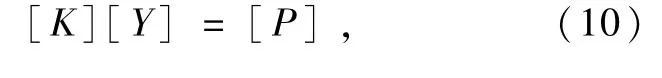
式中:[K]为(mL +1)×(mL +1)阶刚度矩阵;[Y]与[P]分别为mL +1阶桩身水平位移矩阵与水平荷载矩阵。
通过求解式(10)得到桩身位移矩阵[Y],具体计算方法参考文献[17]。图3中初值矩阵[Y0]可按式[K0][Y0]=[P]计算,其中[K0]可按m法[16]确定。
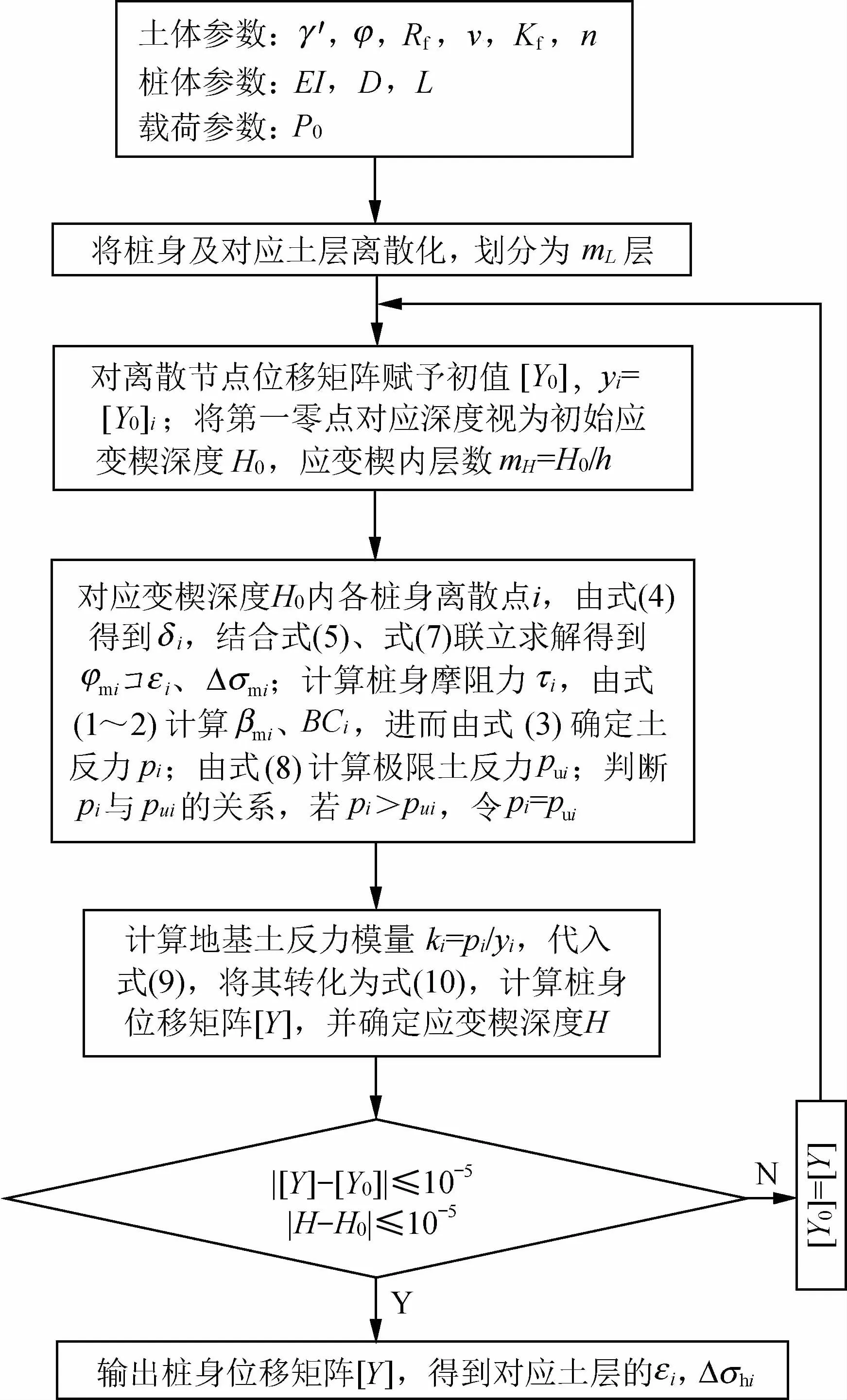
图3 改进应变楔模型计算流程图Fig.3 Flow chart for procedure ofmodified SW model
1.2 刚度衰减模型
水平静力荷载作用下,应变楔模型中土体受力状态类似于静力三轴试验。由于海上桩基所承受的长期循环荷载频率一般较低,因此对于砂土地基,此时桩侧土体受力状态类似于不排水循环三轴压缩试验(竖向应力′相当于试验围压,水平应力增量Δσh相当于循环偏应力σcyc)。如图4所示,在砂土不排水循环三轴试验中,随着循环应力作用次数N增加,累积塑性应变不断增加,砂土割线刚度EsN不断减小,这将会导致桩基位移增大、承载力不断弱化。采用合理的方法描述与EsN随循环次数N的变化过程,对于研究循环荷载作用下桩基性状至关重要。许多学者基于循环三轴试验结果对-N试验曲线进行拟合,采用实用经验计算公式描述累积塑性应变的增长过程,并在实际工程中得到了广泛应用。其中Huurman[18]引入2个砂土循环参数b1、b2近似描述砂土累积塑性应变的发展过程,
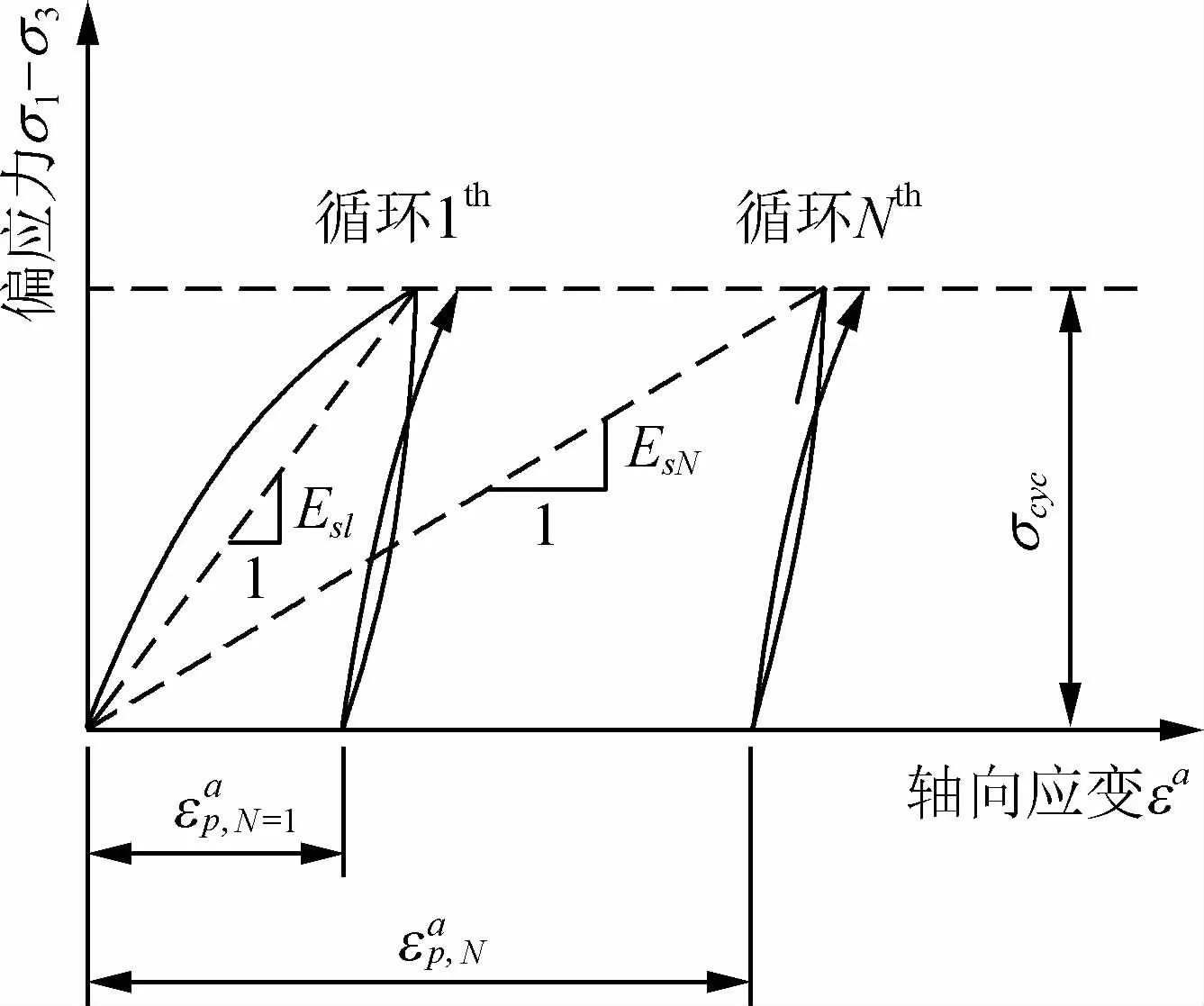
图4 循环荷载作用下砂土割线刚度的衰减Fig.4 Degradation of sand secantmodulus under cyclic loading
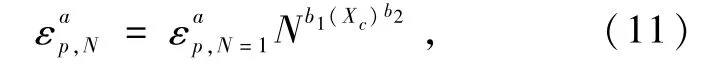
Xc反映了循环应力幅值对砂土循环特性的影响,因此本文基于上述经验公式,结合图4,当不考虑弹性应变时,采用下式计算砂土弱化割线刚度EsN,

式中:Es1为第一次循环应力作用下的割线刚度。KUO Y S[8]通过对现有文献砂土循环三轴试验数据进行拟合,得到b1,b2的取值分别为:紧密砂土,b1=0.2,b2=5.76;中密砂土,b1=0.16,b2=0.38。
1.3 循环荷载作用下桩基侧向位移计算过程
对于荷载幅值为Pmax、作用次数为N的单向水平恒幅荷载循环作用下的桩基,可利用上述改进应变楔模型与刚度衰减经验计算公式确定其侧向位移响应。首先基于拟静力法的思想,采用改进静力应变楔模型计算循环荷载幅值Pmax作用下桩侧土体应力沿地基埋深的分布规律。试验研究[9]表明,单向循环荷载作用下桩侧土体应力呈半正弦规律变化,且有限元计算结果[6-7]也验证了将第一次循环荷载幅值作用下的应力水平作为循环应力水平的可靠性。因此,以上述静力应变楔计算得到的应力状况确定桩侧土循环应力比分布,然后根据刚度衰减经验公式计算N次循环荷载作用后桩侧土的衰减刚度,最后将其引入应变楔模型,对桩基位移响应进行计算,具体计算步骤如下。
(1)确定桩侧土循环应力比。令P0=Pmax,输入桩基和土体参数,代入流程图3,基于改进应变楔模型对荷载峰值Pmax作用下的桩基水平响应进行计算,得到桩侧不同深度离散层土体水平应力增量Δσhi和水平应变εi。令σcyci=Δσhi,将Δσhi视为循环偏应力幅值,利用式(6)计算各离散点土体静偏应力强度σsfi,进而确定相应的循环应力比Xci=σcyci/σsfi。令,将εi视为循环应力第一次作用下的土体应变。
(2)计算桩侧土累积应变和衰减刚度。将桩侧各离散土层的循环应力比Xci代入式(12),计算N次循环荷载作用后所有土体离散点的衰减刚度EsNi和累积塑性应变其中Es1i=可根据邓肯-张模型计算,

其中:Euri为加卸载弹性模量,为Eini的1~3倍[14]。
(3)确定第N次加载过程中土体应力-应变关系。如图5所示,与静力应变楔模型中的土体应力加载过程不同,由于桩侧土体存在累积塑性应变,土体刚度发生衰减,则桩侧土在第N次加载过程中的应力-应变关系可近似为,
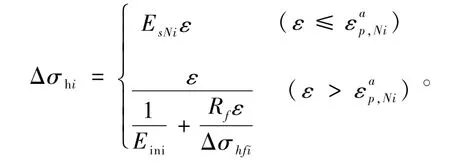
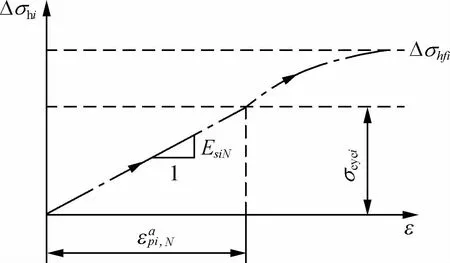
图5 第N次加载过程中土体应力-应变关系Fig.5 Relations of stress-strain of the soils during the N th loading process
(4)对静力应变楔模型进行修正。令P0=Pmax,用式(14)代替式(5),代入应变楔模型计算过程(图3)中,考虑循环荷载对桩侧土体的影响,计算得到水平循环荷载作用下桩身侧向位移响应。据此本文编制了相应的MATLAB计算程序对其进行求解。
2 算例验证与分析
P.Peralta等[19]开展了管桩在不同循环荷载水平作用下的室内模型试验。模型试验中,桩体材料为高密度乙烯,桩径D=63 mm,壁厚度为1.8 mm,嵌入地基深度L=300 mm,抗弯刚度EI=0.162 kN·m2。土体采用级配均匀的中密干砂,相对密实度为40%,不均匀系数为1.5,曲率系数为1,重度为14.79 kg/m3,孔隙比为0.764。模型桩的极限承载力Pu约为50 N。文献[19]采用单向加载进行循环荷载峰值分别为0.5Pu,0.45Pu,0.4Pu及0.2Pu的4组循环加载试验,采用本文简化分析方法计算循环荷载作用下桩基水平响应,本文所采用的计算参数如表1所示。经计算,模型桩相对桩长L/LT=3,其中LT=(EI/ηh)0.2,为相对刚度,属于中短长桩[16]。据此确定计算过程中应变楔深度与桩身第一位移零点关系为H=0.9Z0。刚度衰减公式中的参数取值依据文献[8],取b1=0.16,b2=0.38,在实际工程时,应采取原状土进行室内循环三轴试验,拟合得到刚度衰减公式中的参数,然后代入应变楔模型进行相关工程问题的分析。
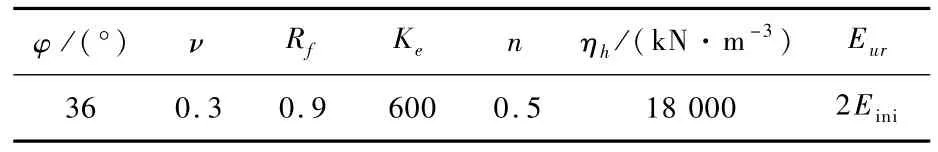
表1 土体理论计算参数Tab.1 Theoretically computed parameters of soil
将本文计算结果与模型试验结果进行对比,不同荷载条件作用下桩头水平位移随循环次数的发展如图6所示,可以看出,当Pmax=0.6Pu及Pmax=0.2Pu时,本文提出的简化分析方法计算结果与试验实测结果较为吻合,虽然Pmax=0.5Pu及Pmax=0.4Pu时计算结果与试验结果略有差别,但位移发展规律基本一致,误差在可接受范围内。结果表明本文方法可以较为准确快捷地计算桩基在长期循环荷载作用下的侧向位移响应结果,进一步说明本文方法的有效性与准确性。此外,p-y曲线法[2]将地基土反力进行折减以考虑循环荷载作用下地基土体弱化的影响,据此本文还在图6中给出了p-y曲线法的计算结果。由图6可知,不同荷载幅值下p-y曲线法计算得到的位移结果为一定值,相较于初次加载情况下位移有一定幅度增加,一定程度上反映了桩侧土的弱化,但计算位移与实测结果及本文计算结果相比,不能反映出循环荷载作用次数的影响。
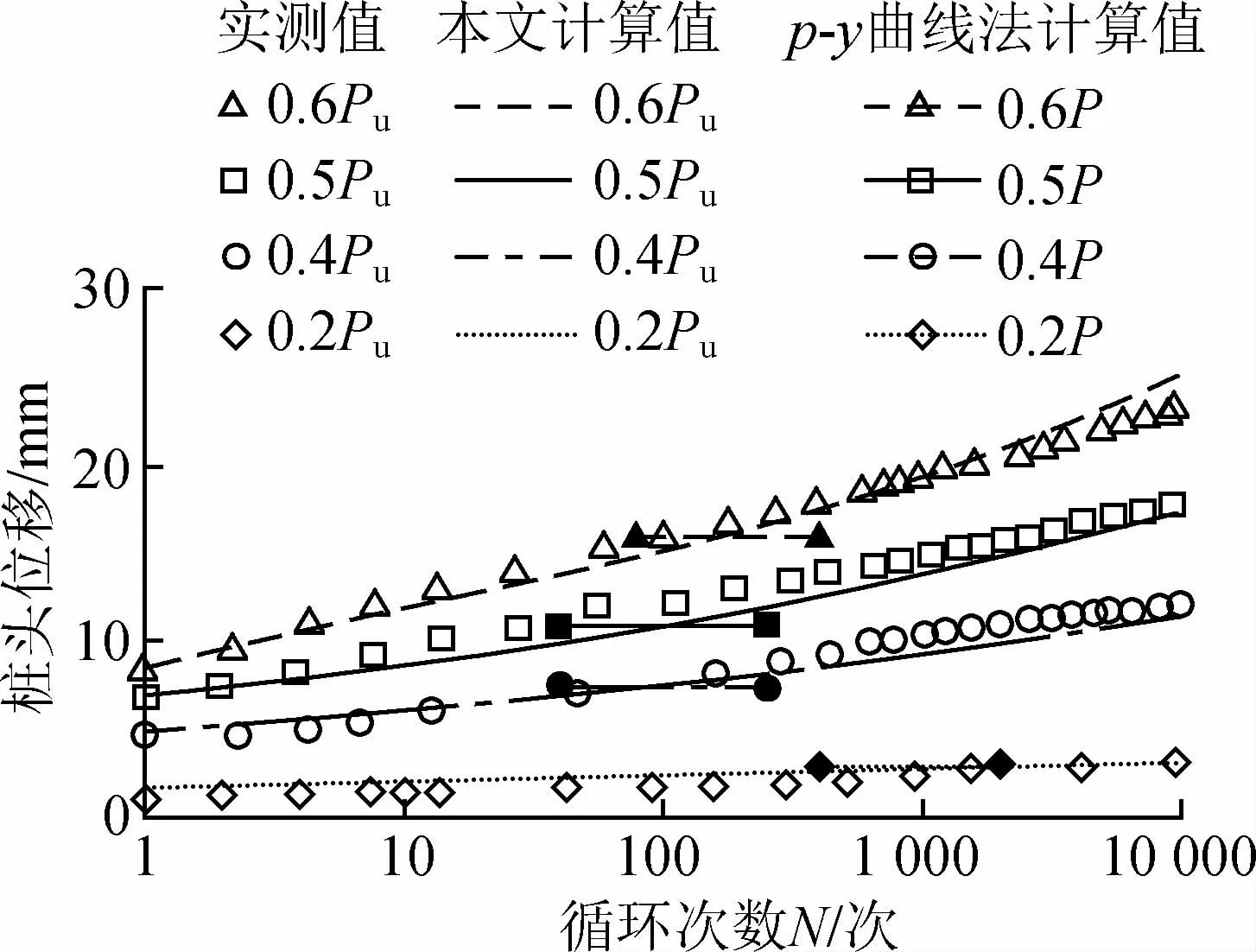
图6 不同方法计算结果与模型试验结果的对比Fig.6 Comparisons between calculation results of differentmethods and model tests
图7为桩基分别在Pmax=0.45Pu与Pmax=0.2Pu荷载作用下桩身水平位移分布随循环荷载作用次数的发展情况。随着循环次数增加,桩身水平位移不断发展。当Pmax=0.2Pu时,循环荷载幅值较小,桩身各处侧向位移随循环次数的增大而增大,当N=7 000或10 000时,桩身位移基本保持一致,趋于稳定。当Pmax=0.45Pu时,荷载幅值较大,桩身各处位移在较大次数循环后不再保持稳定,而是不断增长,说明循环荷载幅值大小和循环次数均对桩身位移响应影响较大,图6也揭示了这一现象。一般情况下,桩身泥面处位移极限值应当不超过桩径的20%,若以此为标准,根据计算结果,当Pmax=0.27Pu时,10 000次循环后泥面位移约达到0.2D,因此对于本例,循环荷载幅值极限值应当不超过桩基静极限承载能力的27%。由此可见,循环荷载作用下,桩基水平承载能力存在较大程度的弱化,在循环受荷桩的设计阶段,应更加注意荷载幅值的大小,保证桩基稳定性。

图7 不同循环次数作用下桩身位移分布Fig.7 Lateral deformation distributions of pile under different cycles
3 结论
(1)本文简化分析结果与室内模型试验结果吻合程度较好,表明本文方法能够真实反映桩基础在水平循环荷载作用期间侧向位移发展情况。
(2)循环荷载幅值较小时,桩身各处侧向位移的发展随循环次数增大而趋于稳定;当循环荷载幅值较大时,侧向位移不断增长,且不再保持稳定。
(3)循环荷载作用下,桩基水平承载能力将出现较大程度的弱化,桩基设计时,应该考虑荷载幅值大小,避免侧向位移过大。
本文方法相比于有限元法在计算上较为简单,无需建立复杂的有限元模型。较p-y曲线法能更有效地反映桩侧土体弱化程度,且能够考虑循环荷载作用次数的影响。本文研究目前仅限适用于单向恒幅循环荷载条件,对于变幅循环荷载条件下桩基性状的计算仍需进一步研究,以便为实际工程设计提供参考。
