基于MEA-BP神经网络的超声挤压加工表面粗糙度预测
2021-10-25陈爽张志肖锦初胡家进赵录冬
陈爽,张志,肖锦初,胡家进,赵录冬
(江西理工大学 机电工程学院,江西 赣州 341000)
0 引言
随着精密和超精密零件加工技术的飞速发展,零件的加工精度和表面质量成为衡量一个国家技术力量的重要标志。超声挤压加工作为现代制造业广泛应用的一种先进加工技术,具有高精度、高质量和高效率等优点[1]。在实际工程中,零件的表面粗糙度对零件的性能会产生很大的影响,例如耐腐蚀性、抗疲劳强度等,因此,在超声挤压加工前,对工件表面粗糙度进行预测不仅可以为参数的选择和表面质量的分析与控制设计提供依据,而且还可极大地减少材料加工时间、降低生产成本,具有重要的实际作用。
国内外学者对超声挤压加工的零件表面粗糙度作了大量的研究。张勤俭等[2]对车轴钢进行超声挤压强化,使表面粗糙度由原来的3.746μm降低到了0.2μm左右;王晓强等[3]对轴承套圈进行了超声挤压加工,并利用响应曲面法建立了工件转速、进给速度和预挤压力等参数与表面粗糙度之间的预测模型;崔凤奎等[4]在王晓强等研究的础上分别运用响应曲面和BP神经网络方法,建立超声挤压加工表面粗糙度的预测模型,结果表明响应曲面模型相对误差控制在6.5%,而BP神经网络相对误差为5.06%,与响应曲面预测模型相比较精度更高。
BP神经网络的初始权值和阈值不同容易导致计算不收敛或陷入局部极值,从而导致预测误差较大[5],为了提高预测模型的精确性和实用性,本文利用思维进化算法(MEA)的全局搜索能力对BP神经网络进行优化[6],并使用优化后的权值和阈值建立新的超声挤压加工工件表面粗糙度预测模型。
1 实验
1.1 实验条件与方案
本实验选用调制处理过的45号钢作为实验材料,规格为直径28 mm的棒材。实验所用超声振动挤压强化系统包括HK30HS型压电陶瓷换能器和电源控制柜、换能器、变幅杆、挤压工具头以及广州数控CK6136S数控车床。其加工系统图见图1、超声挤压加工见图2。为了证明理论的合理性,根据超声振动挤压强化原理,将机床的主轴转速、工具头的进给速度、振幅、挤压力和挤压压力次数作为主要的工艺影响因素,并且保证其他一些参数恒定不变,表面粗糙度为输出结果,设计正交实验,如表1所示。

图1 超声挤压系统图Fig.1 Ultrasonic extrusion system diagram

图2 超声挤压加工局部图Fig.2 Partial view of ultrasonic extrusion processing

表1 实验因素及水平Tab.1 Experimental factors and levels
对45号钢的轴零件进行精车后,将超声振动挤压强化设备夹紧在车床上,并对零件进行超声振动挤压强化实验。实验结束后使用SRM-1(D)表面粗糙度测量仪测量加工后的试样。为了保证数据的精确性,每个部分测量3次求取平均值。将获得的数据用做训练数据样本,见表2。
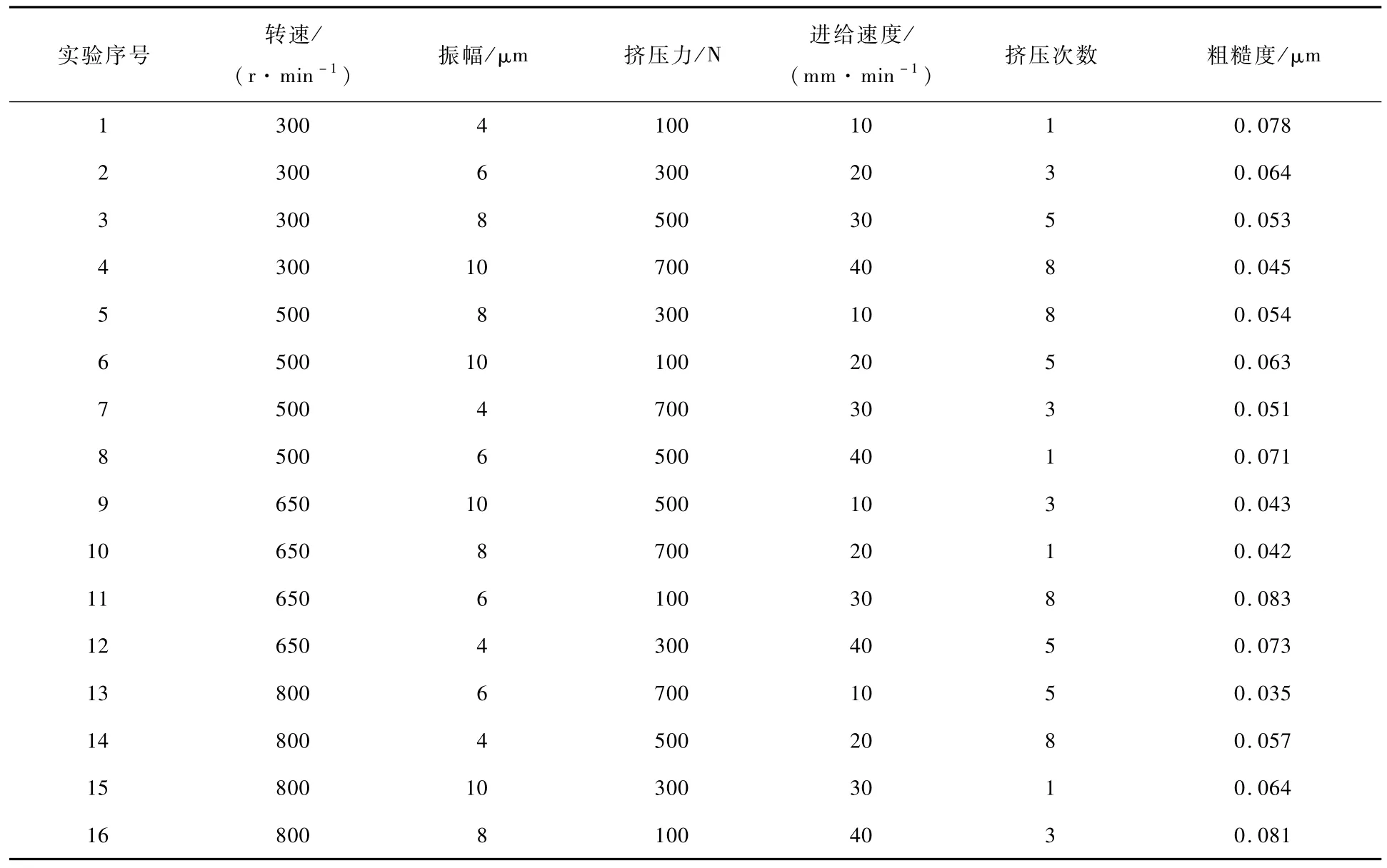
表2 表面粗糙度实验结果Table 2 Experimental results of surface roughness
1.2 实验模型性能评估标准
为了便于直观比较预测模型的有效性,使用均方根误差(RMSE)与决定系数(R2)、平均绝对百分误差(MAPE)定量评估预测模型的性能[7]。为了避免随机参数的影响,分别进行5次实验,并将平均值作为输出。

式中:SSres为回归平方和;SStot为总平方和;SSreg为残差平方和。
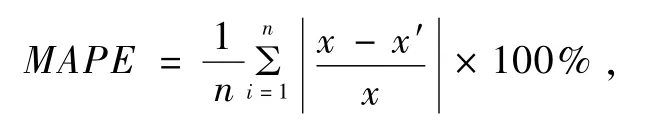
式中:n为样本数;x′为预测模型的输出值;x为真实值。
2 模型构建
2.1 BP神经网络
BP神经网络是具有多层次的拓扑结构的前反馈神经系统,通常具有一个输入单元,一个隐藏单元和一个输出单元。BP神经网络的学习规则核心是最速下降法。利用这种方法逆向传播不断地调整优化神经网络的权值和阈值,使得神经网络的误差达到最理想情况。本实验构建三层结构的BP神经网络,输入层包括转速、进给速度、振幅、挤压力和挤压次数5个影响因素,输出层因素是加工后的表面粗糙度。具体训练过程如下。
(1)神经网络初始化。其中n为输入层节点初始化,m和l分别为隐藏层节点和输出层节点,Wij为输入层和输出层之间的神经元的连接权重。Wjk为隐藏层和输出层之间的神经元之间的权重,a和b为隐藏层和输出层的初始阈值。学习效率η和神经元激发函数f如果固定为固定值,则通常以[-0.5,0.5]间隔的随机数对神经网络的权重和阈值进行随机初始化。
(2)计算隐含层输出。
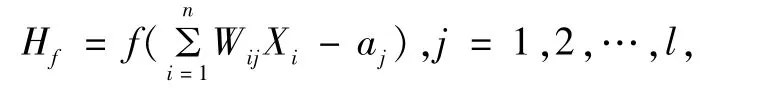
式中:X为输入变量;Hj为隐藏层的输出。
(3)计算输出层的输出。
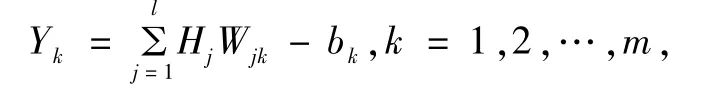
式中,Yk为输出层。
(4)计算误差。由预测输出Y和O计算误差。
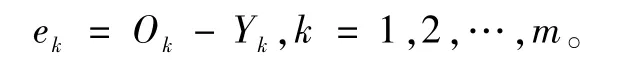
(5)权重和阈值的优化。通过步骤(4),如果误差不满足终止条件,将继续更新权重和阈值,通过不断的重复训练后,获得最佳权重和阈值。
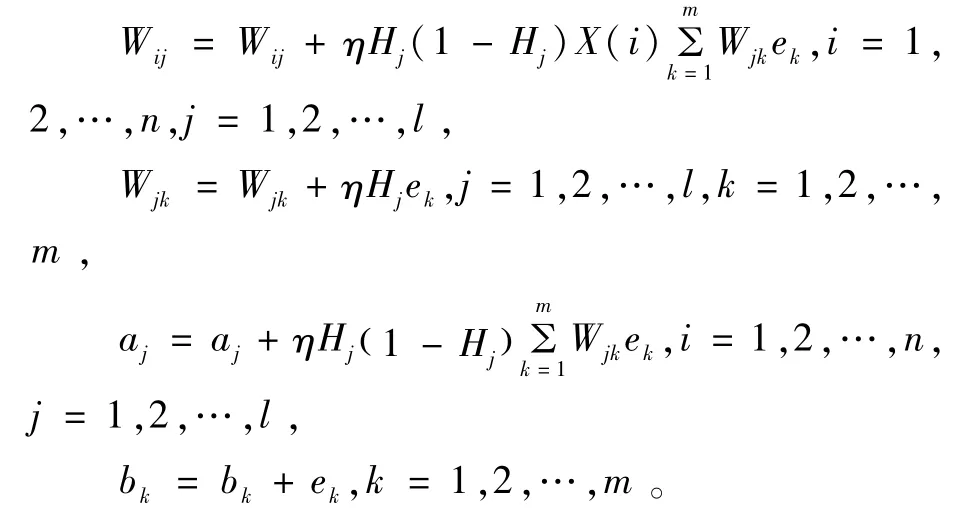
2.2 GA-BP神经网络
遗传算法(GA)将生物进化原理“优胜劣汰”引入到优化参数形成的编码种群中[6-8]。它的核心部分也和生物的遗传基因重组相似,就是通过不断地选择、交叉和变异筛选个体。根据选择的适应度函数,利用遗传规则对个体进行筛选,保留适应度高的个体,剔除适应度低的个体[9]。新种群不仅继承了上一代的信息,而且优于上一代,这个循环会不断重复,直到收敛于最佳的染色体(问题全局最优解),根据编码规则对这个最佳染色体进行解码,即用于建立BP神经网络模型初始权值和阈值[10-1]。
2.3 思维进化算法
思维进化算法(MEA)和遗传算法(GA)中的一些概念具有很多的相同点,同时也是一种通过不断学习进行不断优化的算法。它通过趋同和异化操作不断进行迭代优化[12-13],在解空间中随机生成个体,并且几个个体组成一个组,随机选择其中几个小组作为优胜小组,其他小组被保留为临时小组。按照一定规则计算得分,根据得分情况对所选择的优胜子体和临时子体进行趋同或异化来完成子体的替换或废弃,进而完成筛选,直到得到满足条件最优个体及其得分[14]。BP神经网络对输入单元和隐含单元、隐含单元和输出单元之间的神经元的初始连接权重以及隐含单元和输出单元的初始阈值非常敏感。如果这些参数不合理,收敛速度将会变得很慢,并且网络将陷入局部最优[15]。MEA-BP的主要实现过程可以描述如下。
(1)选择数据集。与传统的前馈神经相同,需要选择足够数量的具有代表性的样本。这样使得建立的模型具有良好的泛化性能。
(2)初始种群产生。利用MATLAB初始种群产生函数可以方便地产生初始种群。
(3)子种群趋同操作。生成上级和临时子种群后,对每个子种群执行收敛运算,并设计误差函数来判断每个子种群是否成熟。如果成熟,则收敛操作结束。
(4)子种群异化。当子种群成熟时,每个子种群的分数将发布在全局广告牌上,这些子种群将执行优胜子种群和临时子种群之间的异化操作。
(5)分析最优个体。当完成足够的迭代操作或找到全局最优个体时,输出最优个体,以获得BP神经网络权重和阈值。
(6)训练BP神经网络。将经过思维进化算法优化过的权值和阈值赋予BP神经网络,对训练集训练。
3 实验分析
3.1 预测模型
经过预测模型的训练后,MEA-BP的趋同和异化结果分别如图3~4所示。可以清楚地看出,训练样本经过2次操作就终止了,这意味着每个子种群均已成熟,即得分不再增加。图3(a)中子种群1的分数没有变化,就是说在子组1的中心附近找不到最佳个体。当种群都成熟后,如果临时分组的得分高于上级分组,则进行异化操作,否则不需要进行操作。
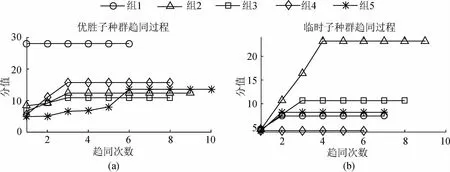
图3 种群趋同过程Fig.3 Population convergence process
比较图3(a)和(b)可以看出,临时子种群2的得分高于优胜子种群1,因此只需要进行1次异化操作并将新子种群添加到临时子种群。观察图4可以发现,在图4(a)中每个小组的得分情况是不变的,因为他们已经成熟。通过比较图4(a)和(b),当优胜子种群和临时子种群成熟后,此时优胜子种群相对应的种群得分都高于临时子种群,则这种情况就满足了算法的基本要求,同时也完成了对权值和阈值的优化。

图4 种群异化过程Fig.4 Population alienation process
3.2 BP与GA-BP以及MEA-BP模型结果分析
建立BP神经网络的预测模型,通过引入思维进化算法(MEA)优化BP神经网络的权值和阈值。将优化前后的模型结果与GA-BP的预测结果进行对比,结果如表3所示,预测集结果对比如图5所示。
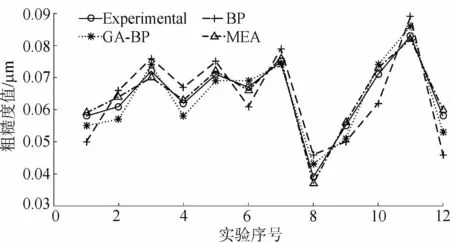
图5 预测集预测结果对比Fig.5 Comparisons of validation results for the prediction set
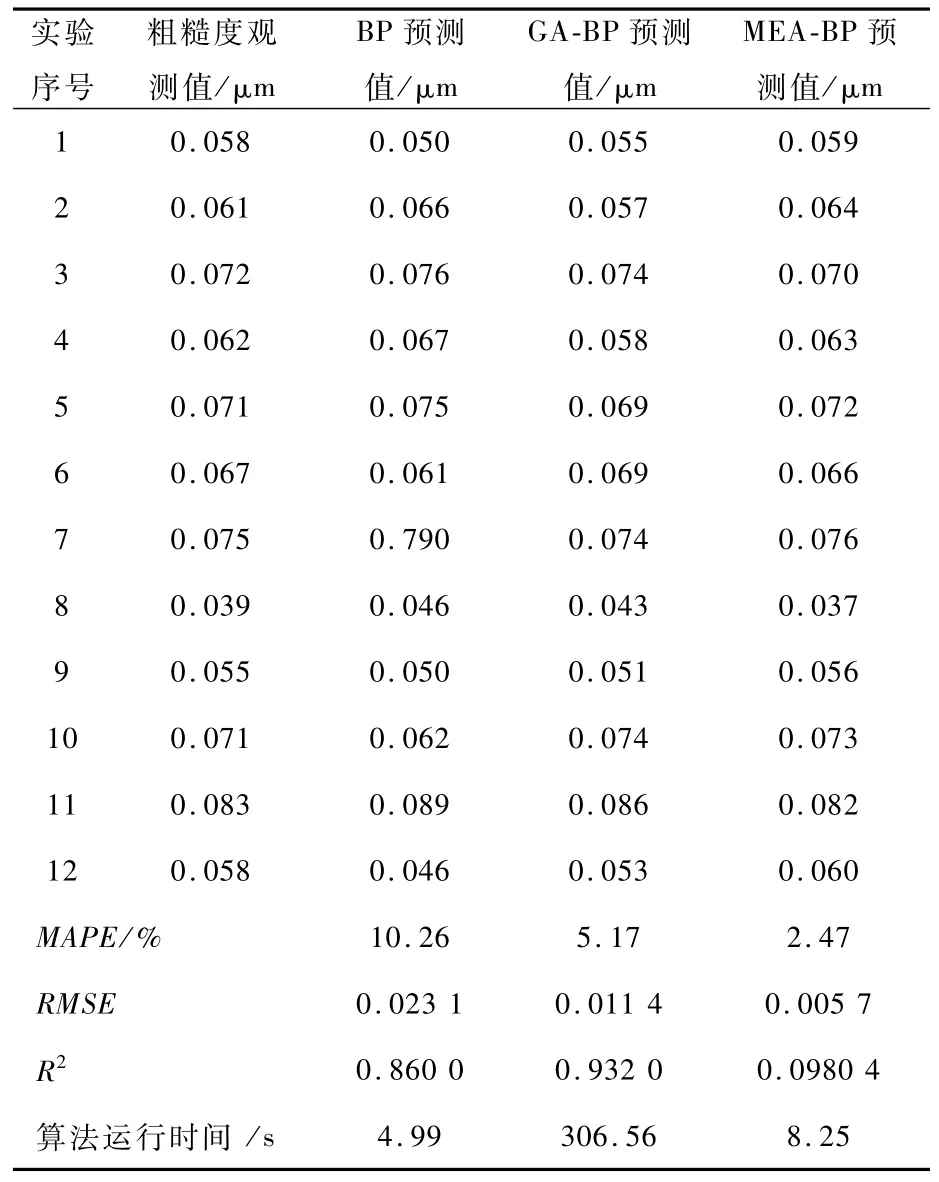
表3 BP与GA-BP和MEA-BP模型结果比较Tab.3 Comparisons among BP,GA-BP and MEA-BPmodels
从表3可以看出,当采用BP神经网络模型进行表面粗糙度预测时,平均绝对百分误差(MAPE)为10.16%,均方根误差为0.023 1,预测集的决定系数只有0.860 0,但是在采用GA-BP预测时表面粗糙度的MAPE为5.17%,均方根误差为0.011 4,决定系数为0.932 0,在使用MEABP预测模型时MAPE达到了2.47%,均方根误差为0.005 7,预测集的决定系数达到了0.98以上。上述的定量分析表明,MEA-BP的预测效果要好于GA-BP和BP神经网络。与遗传算法中的交叉和变异操作不同,MEA可以记住上一代的进化信息,这可以在正确的方向上指导相似性和异化性操作。因此,MEA-BP具有比其他方法更好的预测和概括能力,而且运算时间大幅度减少。
4 结论
(1)本文提出一种将思维进化算法和BP神经网络相结合有效预测超声振动挤压加工表面粗糙度的方法。通过不断优化BP神经网络的权值和阈值,提高神经网络的泛化能力、全局优化能力,使得预测模型更加精确和通用。
(2)通过具体实验的定量分析对BP神经网络与GA-BP以及MEA-BP的预测结果进行比较,结果表明:在相同环境条件下,BP神经网络预测误差较大,GA-BP和MEA-BP神经网络预测模型预测误差想接近,但是MEA-BP所用的时间远远低于GA-BP的。
