地表水平正反敲击激振下孔法剪切波速测试理论依据讨论

肖妍姗，周正华，苏杰，魏鑫

(1.南京工业大学 交通运输工程学院，江苏 南京 210009； 2.黑龙江中医药大学附属第一医院，黑龙江 哈尔滨 150040)

0 引言

土体S波波速是一重要的土体动力特征参数，包括场地动剪切模量的确定、场地地震反应分析、场地类型判别、地震液化场地液化势确定等均需要土体S波波速这一参数[1-7]。目前工程中土体S波波速多通过现场S波速测试获得，如单孔法、跨孔法等钻孔侵入法[4,8-9]及面波法(SASW、MASW)等非侵入法[5,9-10]。通常利用钻孔测试的侵入法被认为可获取较好的测试结果，因其不需如面波法进行反演计算，而是基于观测点与源或观测点间S波传播时间来直接计算S波波速，S波测试深度较深。而在钻孔侵入法中，地表水平正反敲击激振下孔法由于其特有的优点而被工程测试广泛应用。与钻孔跨孔法相比，地表水平正反敲击激振下孔法钻孔数量较少，并能与工程场地勘察钻孔共用，更为经济，且现场测试操作简易等。

在地表水平激振作用下，弹性波在土体中传播并被置于孔内检波器检测到，从而获得不同方向上的位移或速度波形，检波器在孔内由下而上或由上而下按一定的间距移动，在每个点均进行多次激振波形记录，并获得一次有效的高质量波形记录，继而形成土体按深度分布的波形图。通过对获得的波形进行震相识别并分析，以获取波在土体中的传播时间，因此如何准确地判断S波初动并确定出剪切波的传播时间至为重要。由于现场测试不可避免地存在噪声干扰，从单一波形中直接分辨出S波的准确到时较为困难，工程上常应用的水平正反敲击下的反相判别方法来确定每个深度波形中S波的初动，并据此确定S波到时，由此计算出S波在不同深度的旅时，进而计算得到一定土体区间内S波波速[11]。这一方法的理论依据认为，在水平正反敲击下钻孔内位移型或速度型检波器可接收到一组三分量(两水平分量、一垂直分量)P波不反相而S波反相的波形，从而据此识别出S波初动[11]。然而实际测试中，时有发现水平正反敲击下P波和S波均反相的现象，与反相法依据相矛盾。究其原因，一方面可能是由于环境噪声干扰导致了同一深度的两组波形的相位差不足以产生明显的反相点，或者波形中剪切波的信号不强导致初动点判断不准确[12-13]，另一方面则可能是在一些波形清晰的信号中，在剪切波到达前出现振幅较小的连续反相波形[9,14]，从而对剪切波反相点初动判断产生误导。这些因素均有可能造成计算得到的S波波速与实际S波波速间存在较大偏差。对于环境噪声干扰，实际测试中可通过增强信噪比、选取干扰较小的时段或测试场点等方法来消除；而对于S波到达前的反相波形，由于其振动振幅小而往往被忽略，并未对其波动性质深入探究。因此，进一步深入了解和认知地表水平正反敲击激振下孔法S波波速测试中获取的信号波形特征，判断下孔法S波波速测试的理论依据成立与否，其研究具有重要的实际应用价值。

本文基于动力有限元方法建立了地表水平正反敲击激振下孔法剪切波速测试三维分析模型，采用时域集中质量动力有限元显式逐步积分方法求解了水平地表敲击下线弹性半空间波动响应，分析了各深度波形特征及下孔法S波波速测试理论依据的合理性。同时，依据地表水平正反激振下线弹性半空间波动解析解，进一步佐证数值模拟结果的可靠性。

1 地表水平正反敲击下孔法S波波速测试理论依据质疑

地表水平正反敲击下孔法S波波速测试中，一般将内置三分量检波器的单个探头置于钻孔内，S波波速测试时，水平敲击置于地表上压重物的枕木两端产生剪切能量，经由反复敲击并通过由下而上或由上而下移动的检波器(图1a)即可采集记录到一组土层波形剖面(图1b)。为得到土层S波波速，地表水平正反敲击下孔法波速测试常依据水平向反相信号进行剪切波初动确定，继而确定S波旅行时并计算S波波速。其方法理论依据为水平正反向激振下，P波信号不反向而S波信号反相，从而认为记录信号波形中第一次信号出现反向的时刻即为S波初动时刻(反相法)[11]。

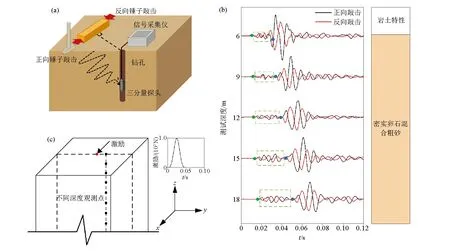
a—地表水平敲击下孔法波速测试示意；b—北京某场地正反向地表水平敲击下孔法S波波速测试获得的记录波形；c—地表水平激振下孔法S波波速测试三维分析模型a—schematic of downhole seismic method with surface plank source;b—signal traces recorded at different testing depth by downhole seismic method at a site in Beijing;c—3D numerical analysis model of downhole seismic method图1 地表水平正反敲击下孔法S波波速测试Fig.1 Surface level positive and negative percussion hole method S-wave velocity test

然而，在实际工程应用中，水平地表正反敲击波速测试下孔法，存在一些让人无法理解的现象，且极易引起S波初动的误判。如图1b是在北京密云区某工程场地进行下孔法波速测试时所测得的不同深度点的信号波形，并应用反相法对测试弹性波波形进行S波初动判断。若将初始出现反相的位置作为S波初动，则图1b中绿色反相点可能被确定为S波初动点，若依据S波幅值大，P波幅值小的特点，则可能将蓝色点确定为S波初动点。依据蓝色点确定初动时间计算得到的波速值约为489.1 m/s，比依据绿色点确定初动时间得到的波速值更接近卵石层的S波波速。本次现场波速测试若以蓝色点确定S波初动，则可以得到一个较接近预测范围的波速值，由此可知，绿色点至蓝色点之间反相波形实际应为P波信号，显然表现的P波反相特征与地表水平正反敲击下孔法波速测试理论判据相佐。若是如此，则水平正反敲击下的P波极性不变而S波极性相反的反向法依据不成立？为了深入研究地表水平正反敲击下孔法S波波速测试理论依据是否成立，在不考虑环境干扰及复杂土层分布条件下，通过应用动力有限元分析方法模拟了地表水平敲击下孔法S波波速测试，以探讨下孔法S波波速测试中信号波形特征和反向法理论依据是否成立，并辅以地表水平正反激振下线弹性半空间波动解析解佐证数值模拟结果的可靠性。

2 地表水平正反敲击下孔法S波波速测试有限元数值模拟

为了模拟地表施加水平正反荷载下土体钻孔内各测点波形，本节将基于动力有限元方法，针对地表水平敲击下孔法S波波速测试建立三维数值模型。首先，引入人工边界从均匀、各向同性线弹性半无限空间中截出一长方体计算区域，其大小为长16 m、宽16 m、高25 m，计算区域上边界为自由表面，底边界与侧边界均设置为人工边界。由Campanella R G等[15]及Ishihara K[16]的理论可知，地表水平敲击下孔法S波波速测试中土体的应变水平处于小应变范围，因此计算区域中土体考虑为线弹性介质，其力学参数列于表1中。在模型水平自由表面中心处作用一水平向(沿X向)时间为0.05s的单位脉冲荷载，其截止频率约80Hz，如图2所示，其中x与y向为水平向、z向为垂直向。计算区域采用三维八节点六面实体有限单元进行离散，其单元尺寸为0.2m，是依据动力有限元计算精度要求确定的。对于计算区域内节点激振位移响应采用时域集中质量动力有限元显式逐步积分方法求解，并依据显式动力有限元时域分析稳定性要求，确定时间步长为 0.000 2s。在计算区域底和侧人工边界上应用二阶多次透射公式(multi-transmitting formula，MTF)[17-20]模拟弹性半空间的辐射阻尼效应，以确保计算区域的散射波场从计算区透过人工边界而不发生反射。

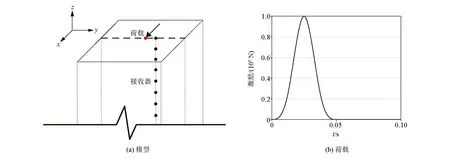
图2 地表水平激振下孔法S波波速测试三维分析模型(a)及荷载(b)Fig.2 3D analysis model(a) and load(b) of S-wave velocity test by hole method under surface horizontal excitation

表1 模型力学参数

在数值模拟分析中，通过改变加力方向来模拟波速现场测试中的正反向敲击，图3给出了数值模拟获得的叠加正反向激振下不同深度测点x方向的位移响应波形。图3a～3c显示了不同深度测点波形中反向加载与正向加载得到的波形相位完全相反，此时若采用地表水平正反敲击激振下孔法S波波速测试的反向法依据，初始反相点应为图3中的TA点，则该点后面的部分应为S波，但经分析实际波的性质并非如此。

由理论分析可知，在固体介质中集中力源激振所产生的波并非“纯粹”的S波，而是P波和S波耦合的效果[21-22]，从而导致激振位移响应波形中没有一个纯粹的S波初动点。那么，前面确定的TA是否是S波初动点，可依据数值模拟中模型土体介质的S波波速值来判断。根据“时间=距离/波速”在各个深度的波形中用TP和TS标记相应深度处P波和S波的初动时间，由此可以发现：表现初始反相的时刻TA并非TS时刻，也不是TP时刻。针对3个深度处(8 m、16 m、24 m)激振位移响应波形前部进行放大(如图3d～3f)，并可看到TP至TS间反向点时刻发生变化，并逐渐趋于TP点，显然因放大而变动部分的激振位移响应波动并非是S波，而为P波；此外，随显示不同幅值比例变化TA位置也发生变化，且逐渐趋近于TP。另一个值得注意的是，无论波形是否放大，反向加载所得到的激振位移响应波形中的P波部分亦同样反相。

a、b、c—部分深度的测点时程曲线；d、e、f—8 m、16 m、24 m测点放大波形示意a、b、c—the original signal traces at different selected depth;d、e、f—amplified waveform of partially signals at observation points with depth of 8 m,16 m,24 m图3 水平正反向激振下不同深度测点x向记录波形Fig.3 Signal traces at different depth observation points in x-direction under the horizontal forward and backward excitation

综上所述，地表水平正反施加荷载所获得的平行敲击方向的位移响应波动中，无论P波还是S波均具有震相反向这一特征，由此可知地表水平正反敲击下孔法S波波速测试判据值得商榷。但由图3也可看出，在已知水平正反向敲击激振的P波反相的前提下，对于实际现场测试也很难准确判断TS点，这主要因为：

1)从图3a中可以看出，浅地表测点信号前部中P波与S波耦合在一起，难以识别出S波初动，即使放大波形(图3d)亦无法识别，且易将P波部分误识别为S波部分，从而造成确定的TA点而非TS点。

2)随着深度增加，由于P波波速大于S波波速的原因两者逐渐分离开来(如图3d、e、f)，但仍无法识别出S波初动，这是因为尽管P波随测点深度增加有较大衰减，但此时P波仍有一定幅值并叠加到S波上，此时通过波形放大只能识别出S波初动的大概位置，且TS位置在不同条件下变化很大。

图3a～3c所显示的波形中，由于幅值小，未明显显示出反向的P波部分，这一特征有可能在实际测试中被认为不存在反相特征，这可能是导致现场S波波速测试中认知错误的原因之一。本文数值模拟结果已证明，地表水平正反敲击激振所产生的位移响应波形未能显现P波不反向而S波反向的特性。但在地表水平正反敲击下孔法现场S波波速测试中，却能观察到P波不反向而S波反向的这一特征，这可能是由于实际测试中的工作状态及背景振动干扰引起的，而本文分析未考虑这些因素的影响，将另文讨论地表水平正反敲击下孔法剪切波速测试在什么条件下才显现出P波不反向而S波反向的这一特征。

3 自由表面水平力作用下均匀线弹性半空间波动解析解佐证

Chao C C等[23]基于理论分析获得了均匀各向同性线弹性半空间在自由表面切向荷载作用下的切向(平行作用力方向)和垂向位移的精确解。进一步利用Laplace变换和Hankel变换，基于半逆方法求解得到了沿作用力加载点垂直向下各点的位移响应，当泊松比为0.25时，切向位移响应可以表示为：

(1)

其中

且F为Heaviside单位阶跃函数，Z为计算点与荷载作用点间垂直距离，μ为剪切模量，vS为S波波速。

为确定式(1)的数值解，本文引入了一近似Heaviside单位阶跃函数，如式(2)所示:

(2)

假设在剪切模量μ=68 MPa、S波波速vS=200 m/s的均匀各向同性线弹性半空间自由表面作用一正反向切向近似Heaviside单位阶跃集中力(图4a)，则可通过式(2)求解得到半空间内沿作用力加载点垂直向下各点的切向位移响应。图4b给出了作用力加载点垂直向下距离2 m和8 m点的切向位移(平行作用力方向)。由于横坐标采用的是无量纲时间，结合给定的泊松比，横坐标0.577时意味着P波到达时刻，而横坐标1.0时对应的是S波到达时刻。从图4b能明显观察到正反向加载下P波极性与S波极性均反向，后者与荷载的极性保持相同。而在正、反向激振下，P波和S波均表现出极性反转的特性，这一特性与数值模拟所获得的特征一致，这进一步说明地表水平正反敲击下孔法S波波速测试的反相法依据不成立。

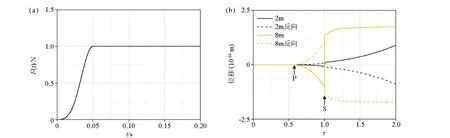
a—近似Heaviside单位阶跃函数；b—正、反向加载下半空间内沿荷载作用点垂直向下2 m和8 m点的位移反应，泊松比为0.25a—approximate Heaviside unit function；b—displacements at depth of 2 m and 8 m in an elastic half-space directly below surface tangential point source with the poisson's ratio of 0.25图4 近似Heaviside单位阶跃函数沿作用力加载点垂向下各点位移Fig.4 Displacements of directly below surface tangential point source with approximate Heaviside unit function

4 结论及讨论

为了探究地表正反向水平敲击下孔法剪切波速测试反向法依据的可靠性，本文基于MTF的三维动力时域显式有限元方法数值模拟了均匀弹性半空间自由表面正反向水平敲击下孔法剪切波速测试，继而分析了地表正反向水平敲击下弹性半空间位移响应信号波形特征，结果表明：通常所认为的地表正反水平敲击下孔法剪切波速测试反向法依据不成立，即：在正反向水平荷载作用下，平行加载方向上的位移信号波形中无论P波还是S波均相位相反。因此，由地表正反向水平敲击下孔法剪切波速测试反向法依据判断的初动点并非S波初动，这将对S波波速计算结果产生影响。此外，本文亦通过地表水平正反激振下线弹性半空间波动解析解佐证了数值模拟结果的可靠性。

尽管本文数值模拟模型和理论分析模型均为弹性半空间模型，但其分析结果不失普遍性，仍能反映地表正反向水平敲击激振下孔法剪切波速测试中观测点波形特性，揭示了地表正反向水平敲击激振下孔法观测点水平向波形中P波发生反相这一与实际认知矛盾的现象，并指出了应用其确定剪切波初动时刻的不合理性。本文研究对于如何利用地表正反向水平敲击激振下孔法来获取土体的S波波速具有重要的参考价值。