固定航路飞行条件下的无冲突航迹规划
2021-10-23胡明华南京航空航天大学民航学院南京211106
周 逸,胡明华,张 颖(南京航空航天大学 民航学院, 南京211106)
随着民航运输需求的快速增长,空中交通流量持续增加,给现有的空中交通管理系统带来了巨大压力,成为航空业发展中面临的一个重要的问题.为保障未来交通需求增长下空中交通的安全高效运行,提出了基于航迹的运行概念(Trajectory Based Operations, TBO),TBO为空中交通管理提供更加丰富和准确的航班运行信息,使得在战略阶段通过航迹规划解决潜在的飞行冲突成为了可能[1].战略阶段的无冲突四维航迹规划有利于保障飞行安全,提高空域的使用效率及航班运行的经济效益,同时降低战术阶段冲突解脱造成的管制负荷[2-3].
在战略规划阶段对航空器之间的潜在冲突进行探测与解脱,已成为国内外许多学者关注的问题.欧控提出的STREAM项目研究针对大量航迹的战略冲突解脱算法,利用新的数据结构优化基于网格的冲突探测方法,同时考虑到冲突解决的“多米诺效应”,提出因果模型解决冲突避让的相互影响[4-5].NASA提出的Stratway项目研究模块化的战略冲突解脱方法,根据输入的航空器意图信息,通过成对冲突探测方法识别航空器潜在的飞行冲突,并利用启发式算法生成一系列机动动作以保证航空器无冲突并满足一定约束条件[6-7].Guan等采用协同进化算法结合动态分组策略,对大规模战略冲突解脱问题进行求解[8].Liu等结合蚁群算法和人工势场法,提高冲突解脱问题的求解效率[9].
上述研究以最小化航迹之间的潜在冲突为主要优化目标,然而从空中交通整体运行效率方面考虑,若仅关注飞行安全可能会出现航班飞行成本过高和航空公司飞行成本分配不均衡的情况,不符合TBO概念中与用户进行协同决策的理念.因此,本文将最小化航迹成本和最大化航空公司间成本分配的公平性作为目标函数,建立双目标的战略冲突解脱模型,采用基于固定航路的冲突探测方法进行冲突探测,通过调整离场时间、改航和高度层分配解决潜在冲突,采用混合元启发式算法对模型进行求解,最后采用实际数据对算法效能进行评估.
1 多目标航迹规划模型
固定航路飞行条件下的空域结构表示为一个封闭的区域S⊃R3,其垂直空间被划分为一组飞行高度层L,水平空间由有向图(N,E)表示.其中:节点N表示航路点,弧E表示航路.为了方便计算,本文将地球表面的经纬度通过高斯克吕格投影转换为(x,y)坐标,其投影的中心位于空域的中心.本文只考虑航班巡航阶段的冲突解脱, 因此假设航迹的起止点为爬升和下降的顶点,同时假设航班准确按照既定的航迹以均匀的巡航速度飞行.
1.1 决策变量与目标函数
本文引入以下0-1变量作为决策变量
由于避让潜在冲突可能会导致航空器的飞行航迹偏离计划航迹,造成额外的飞行成本,因此本文首先关注最小化航迹调整成本(Total Trajectory Amendment Cost,TTAC),该成本由地面延误成本(CostGH)、所选航路飞行成本(CostRT)以及飞行高度层分配成本(CostFL)三部分组成:
minTTAC=(λGHCostGH+λRTCostRT+λFLCostFL)
(1)
其中:λGH,λRT,λFL分别为三个部分的成本系数,表示这三种成本对于航空公司的相对重要程度.
1)地面延误成本
由于模型属于战略阶段规划,在冲突解脱过程中不涉及空中等待和调速等手段,因此只考虑离场时间调整导致的地面延误成本.
(2)

2)所选航路飞行成本

(3)

3)飞行高度层分配成本
航班偏离其参考飞行高度层会导致额外的成本.
(4)
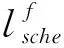
在冲突解脱过程中,若只考虑航班的飞行成本,生成的方案可能会为了规避冲突和减少成本,使得部分航空公司承担较高的航迹调整成本,导致航空公司之间的航迹调整成本(Airlines Total Trajectory Amendment Cost, ATTAC)差异过大,影响空中交通运行的公平性.因此,本文引入基尼系数作为衡量战略冲突解脱公平性的指标[10-11],将最小化基尼系数作为目标函数,确保航迹调整成本在各个航空公司的分配更加均衡.
(5)
(6)
其中:Fa为航空公司a的航班集合.
1.2 约束条件
1.2.1 冲突约束
当航空器间距不满足最小间隔要求,即水平距离小于5海里且垂直间隔小于300 m时,认为航空器存在冲突[12].由于传统的成对冲突探测方法需要大量计时间,本文采用了基于固定航路的冲突探测方法[13].在固定航路网络结构中,航空器之间的潜在冲突仅会出现在节点和弧上,因此引入两种不同的变量和分别表示在节点CN和CE弧上的冲突数量.
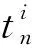
(7)
其中:θi,j∈(0,π)∪(π,2π)为两架航空器的夹角,D为水平安全间隔标准.

因此,固定航路网结构下的航空器冲突总数表示为节点冲突数量和弧冲突数量之和:
CTotal=CN+CE
(8)
当所有航空器之间的冲突数量为零的时候,能够保证生成的航迹是无冲突的,即冲突约束表示为:
Φtotal=0,∀f∈F
(9)
1.2.2 其他约束
(10)
(11)
(12)
(13)
1≤rf≤n, ∀f∈F
(14)
(15)

2 混合元启发式算法
为了求解上述大型的多目标优化问题,本文采用了一种混合元启发式算法(Hybrid-Metaheuristic Optimization Algorithm, HMOA)近似计算帕累托前沿解.该算法以概率执行模拟退火和局部搜索算法,通过局部搜索算法加强对潜在可行解附近的解空间搜索,并利用模拟退火算法以概率接受退化解的方式避免算法陷入局部最优,其算法流程如图1所示.

图1 混合元启发式算法流程Figure 1 The flow of HMOA
2.1 算法执行概率计算
1) 执行模拟退火算法的概率
禅意空间为一角落处绿化休憩空间,廊架借其一侧深色卵石草坡入景,禅意的气息也沁入建筑内,如诗情画意般陶醉。
(16)
其中:PSA,min和PSA,max分别为执行模拟退火算法的最大和最小概率,T0和T分别为初始温度和当前温度.
2) 执行局部搜索算法的概率
(17)
其中:PLOC,min和PLOC,max分别为执行局部搜索算法的最大和最小概率.
3) 按顺序同时执行模拟退火和局部搜索的概率
PSL(T)=1-(PSA(T)+PLOC(T))
(18)
2.2 邻域结构与接受准则
邻域结构的定义是混合元启发式算法中的重要部分,通过在当前解中选择一条航迹i进行局部变化以生成邻域解.为了得到更多满足冲突约束的有效解,本文使用轮盘赌选择法选择进行局部变化的航迹.根据冲突探测的结果,若存在冲突,每条航迹根据其冲突数量Φi计算其被选中的概率(与Φi成正比),计算各航迹的累积概率.生成一个在[0,1]之间的随机数,根据随机数所处的累积概率区间选择相应航迹i.若无冲突,则随机选择一条航迹i.对于选定的航迹i,通过地面延误、改航和高度层分配进行冲突解脱.为了使用户能够表达对冲突解脱方式的偏好,本文引入了取值在[0,1]之间的参数PGH和PFL,分别表示对航迹i执行地面延误和高度层分配的概率,对航空器i执行改航的概率则为1-PGH-PFL,其流程如图2所示.
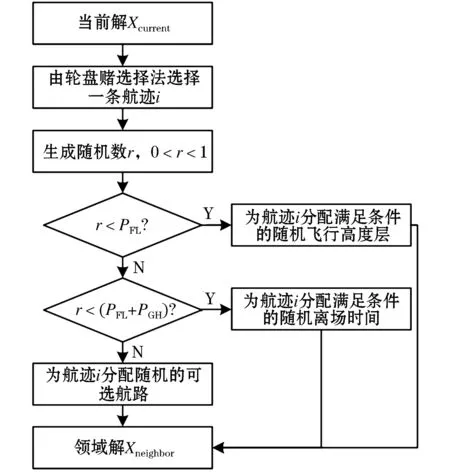
图2 邻域结构流程图Figure 2 The flow of neighborhood structure
算法需要对生成的邻域解进行评估,判断是否接受其作为新的当前解,因此需要规定接受准则:若邻域解不满足冲突约束,则接受冲突数量减少的邻域解.若邻域解满足冲突约束,则对其总运行成本和公平性指标进行评估,算法接受减少任一目标函数值的邻域解.
2.3 模拟退火与爬山局部搜索算法
(19)
其中:ΔE指目标函数值的退化.为了计算ΔE,本文采用加权聚合法,对两个目标函数进行加权求和,并加入了冲突数量作为惩罚值.权重系数的设定需要确保冲突数量函数的所有取值均大于两个目标函数的加权和.若到达给定温度T的最大迭代次数NI,根据Ti+1=α·Ti进行温度递减,重复这一过程直至预先设定的最终温度Tf.
爬山局部搜索算法每次从当前解的相邻解空间中选择一个最优解作为当前解.算法根据上述邻域结构对当前解进行局部变化生成邻域解,接受满足上述接受准则的邻域解作为新的当前解,重复这一过程直至最大迭代次数nI.
3 实验与结果分析
3.1 实验数据
本文采用国内的历史飞行计划数据及航路网络数据对提出的模型和算法进行测试,选取2019年7月3日上午8:00~9:00之间的飞行计划信息,涉及2 122个航路点,58个机场和100架航班,初始航迹根据航班初始飞行计划生成,利用Dijkstra算法得到每个城市对之间的4条最短改航航路作为可选航路[14].仿真实验通过Matlab R2016a进行,实验结果基于20次独立运行得到.
3.2 混合元启发式算法效率
为了有效评估混合元启发式算法的效率,本文以相同的参数设置将其与模拟退火算法的运算结果进行多次对比分析.图3描述了平均冲突总数随着迭代次数的变化.比较混合元启发式算法与传统的模拟退火算法对应的下降曲线,表明混合元启发式算法较模拟退火算法能够更快的降低冲突数量,说明加入局部搜索算法能够有效提高解决航迹之间冲突的效率.此外,本文对两种邻域结构中航迹选择策略进行测试,包括轮盘赌选择和随机选择.对比不同航迹选择策略的曲线,表明本文基于航迹冲突数量进行轮盘赌选择的方法能够显著加快冲突解脱的效率.

图3 不同算法的平均冲突数量下降曲线图Figure 3 Decline curve of the average number of conflicts for different algorithms
由图4可知,对于两个目标函数,混合元启发式算法得到的帕累托前沿解均支配由模拟退火算法所得解,说明混合元启发式算法的求解效率更优.为了能够有效的评价两个算法得到的非支配解集的质量,本文使用了三种评价多目标优化算法常用的指标,分别为超体积(HV),世代距离(GD)和分布(Δ)[15].表1中给出了两种算法所得解的各项指标的平均值和标准差(在括号中表示).对于三种指标,混合元启发式算法的三项指标的平均值均优于模拟退火算法,二者的标准差近似,表明混合元启发式算法求解多目标优化问题的效能优于模拟退火算法.
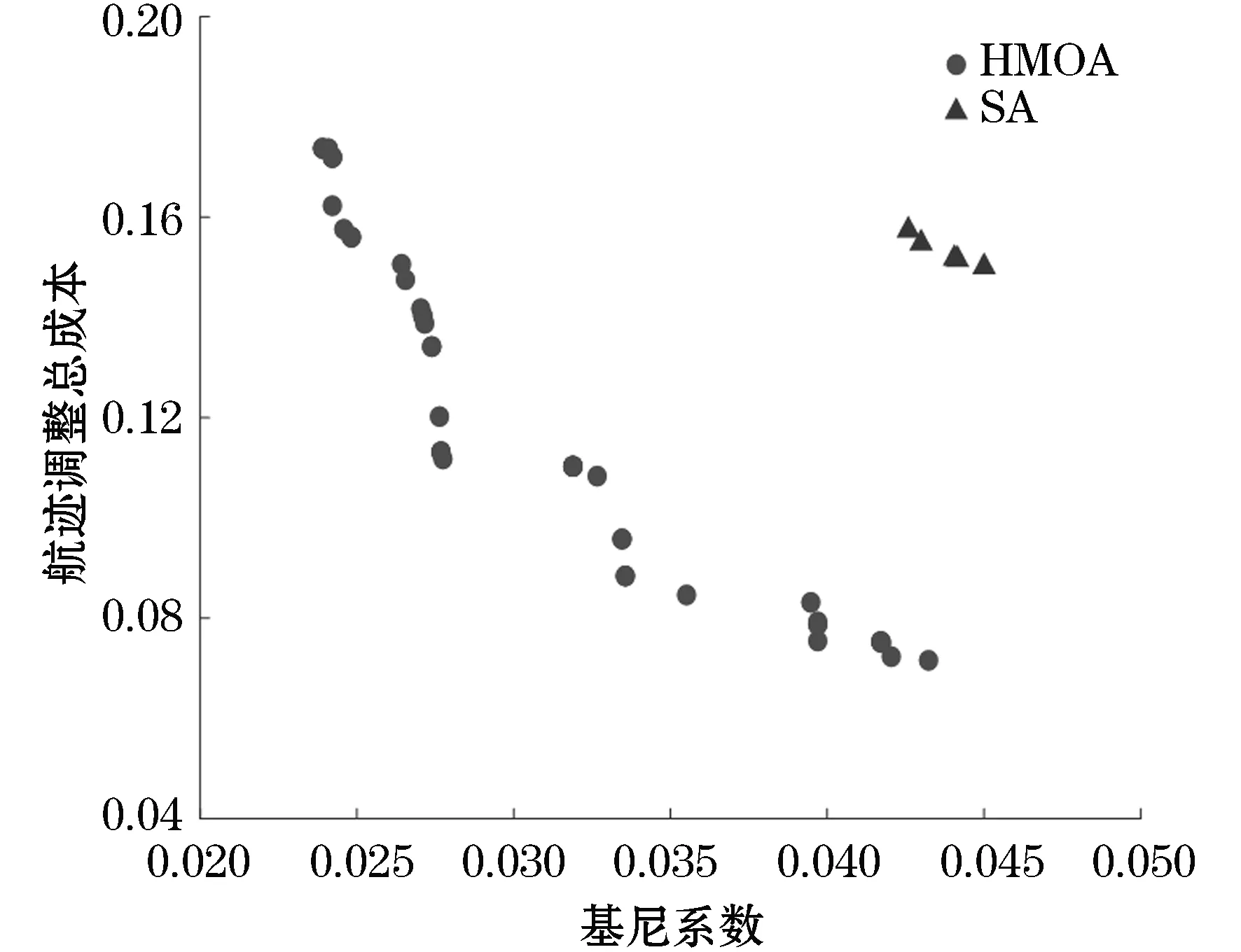
图4 两种算法所得的帕累托前沿图Figure 4 Pareto frontier obtained by the two algorithms

表1 两种算法的求解效率对比
3.3 优化结果分析
如图5所示,分别统计两种算法所得解的地面延误、空中延误和高度层变化的分布情况.地面延误分布方面,两种算法结果中大部分航班能够准时离场,相较于模拟退火算法,混合元启发式算法所得解中未延误的航班比例更高,且各延误时长的航班比例均小于模拟退火算法.对于空中延误分布,两种算法的空中延误时间主要分布在(0,5]分钟区间内,混合元启发式算法的无空中延误的航班比例略高于模拟退火算法.高度层变化分布情况与地面延误类似,两种算法以无飞行高度层改变的航班为主,混合元启发式算法所得解中无飞行高度层改变的航班比例更高,且各高度层改变的航班比例均小于模拟退火算法.

图5 两种算法的地面延误、空中延误、飞行高度层改变量分布情况Figure 5 The distribution of ground delay, air delay, and flight level shift of the two algorithms
如表2所示,分别计算了混合元启发式算法和模拟退火算法所得解的平均地面延误时间(avrGH)、平均空中延误时间(avrAD)、平均高度层改变量(avrFL)和各航空公司之间航迹调整成本分配值的标准差(stdAirlines).三项指标的均值可以说明混合元启发式算法在降低飞行成本方面优化效果更好.根据航空公司之间成本的标准差计算结果可知,混合元启发式算法所得解的航空公司之间航迹调整成本分配差异更小,在公平性指标方面较模拟退火算法获得更好的优化效果.

表2 两种算法的优化效果对比
4 结 语
本文基于固定航路飞行条件下研究了战略阶段的无冲突四维航迹规划问题,建立了多目标无冲突航迹规划模型,利用离场时间调整、改航和飞行高度层分配方式调整航空器航迹,引入了基尼系数作为衡量航空公司之间航迹调整成本分配公平性的指标,将最小化航迹调整成本和最大化公平性作为模型优化目标,实现航迹调整成本和公平性两个目标之间的折中.为了提高对优化模型的求解效率,采用了基于固定航路的冲突探测方法加快航迹间冲突探测,并设计模拟退火和爬山局部搜索算法相结合的混合元启发式算法对模型进行求解.采用我国实际飞行计划和航路网数据对模型及算法进行验证,结果表明,混合元启发式算法在问题求解效率和优化效果方面都比单一的模拟退火算法更优,可以用于有效解决四维航迹战略冲突解脱问题.
