基于CFD 的原油集输管道携水流动特性分析
2021-10-22张鹏祁庆芳程利陈强蒋玉卓吕林林
张鹏 祁庆芳 程利 陈强 蒋玉卓 吕林林
中国石油青海油田分公司管道处
近年来,原油集输管道穿孔现象频繁发生,内腐蚀是造成穿孔的主要因素之一,研究内腐蚀机理是制定管道防腐措施的关键。原油自身不具备腐蚀性,但原油中存在一定的饱和水或游离水,在经过管道的上倾、下倾或弯头等处时形成积液,积液与酸性物质结合,会在管底发生电化学腐蚀,产生的腐蚀产物可堵塞管道,引发管道安全问题[1-2],特别是在管道停输阶段,积水会逐渐向地势较低的地方汇集,对再启动过程影响较大[3]。因此,准确预测积水位置分布、流动特性和携水所需要的最小原油流速对清除管内积水具有重要意义。目前,受限于油水两相流在水平管内的复杂流动状态,多以水平管为对象进行研究[4-7],且传统的两相流试验研究中,油水混合物以恒定流速和相含率进入管道,但本文研究的积水被预先注入管道,模拟管道停输阶段,积水体积不再增加,积水运移的增量全部来自油相的剪切作用和壁面的摩擦,积水移动速度和油水界面形态未知。
经研究表明[8-10],油水两相流瞬态问题的求解可利用计算流体力学(CFD)来进行数值模拟,在此采用Ansys Fluent 建立原油携水流动性模型,利用流体体积(VOF)模型、标准k-epsilon 湍流模型、连续界面张力(CSF)模型对油水界面的动力学模型进行求解,分析油水界面的具体形态,对比不同管壁润湿角条件下的流动特性。
1 原油携水模型
1.1 基本控制方程
由于油水两相共存于同一管道中,两者之间具有一定的密度差,存在明显的相界面,因此选取VOF 模型、标准k-epsilon 湍流模型和CSF 模型跟踪油水两相界面变化情况,连续性方程和动量方程如下
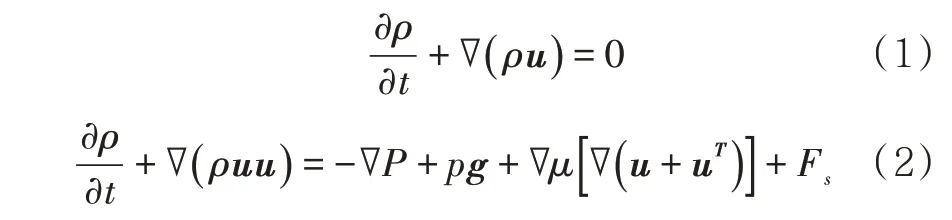
式中:ρ为混合流体密度,kg/m3;t为时间,s;u为流速速度矢量,m/s;p为压力,Pa;g为重力加速度矢量,m/s2;μ为混合流体黏度,N·s/m2;Fs为体积力源项。
由于需要模拟壁面回流及界面失稳状态,在VOF 模型的基础上利用用户接口(UDF)对动量方程进行修正,采用Kelvin-Helmholtz 方法,在动量方程中引入微小波动,通过波动速率确定界面的变化形态。
采用CSF 模型,将界面力以附加源项的形式加入动量方程,如下

式中:σ为表面张力系数;k为界面曲率;a为体积率;ρw、ρo分别为水相和油相密度,kg/m3。
1.2 几何建模
以文献[6]中XU 的实验为原型进行几何建模,其中直管段长500 mm,上倾段长500 mm,倾斜角度12°,管径27 mm,定义油相密度、黏度分别为856 kg/m3、3.43 mPa·s,定义水相密度、黏度分别为997 kg/m3、0.895 mPa·s,油相和水相之间的表面张力为18.33 mN/m。采用六面体网格划分,通过“Patch”功能预先在直管段管底填充一部分积液,几何模型和端口处网格划分如图1 所示。

图1 几何模型及网格划分Fig.1 Geometric model and meshing
1.3 边界条件
采用瞬态计算,入口为速度入口,出口为压力出口,壁面为增强壁面方程,采用无滑移边界条件。求解器选择压力求解,利用一阶显式格式和一阶隐式格式对连续性方程和动量方程进行求解,压力-速度耦合方程采用PISO 非定常格式进行计算,体积分数采用几何重构方式。迭代步数为106,步长为0.01 s,每个时间步长的最大迭代次数为50次,残差设置为10-6。
2 结果与讨论
2.1 结果检验
为验证数值模拟的准确性,对不同原油流速下管道出口处的携水量进行计算,并将计算结果与文献[6]中的实验结果对比,初始条件取管内积液量15 mL、25 mL、40mL,管壁润湿角θ取120°(定义0 到90°为亲水性壁面,90°到180°为疏水性壁面),计算结果如图2 所示。

图2 不同原油流速下出口携水量Fig.2 Outlet water carrying volume at different crude flow rates
由图2 可知,在不同的管内积液量条件下,实验值和模拟值具有良好的一致性。当原油流速低于0.08 m/s 时,出口携水量为0;原油流速大于0.08 m/s 时,出口携水量逐渐增多;原油流速超过0.16 m/s 时,积液被全部带出管道。原油流速在0.08~0.12 m/s 的范围内,数值模拟结果存在偏低的现象,这是由于VOF 模型中油相和水相速度不一致引起了相间滑脱现象,此外在数值模拟的过程中无法完全再现实际管路中内壁粗糙度对水相剪切应力的影响,而毛细效应的存在会使水滴更容易凝结成一个整体,促进了水分子的聚集现象,进而促进液滴的分离和水相的携带。综上所述,不同积液量下的原油携水临界速度均为0.08 m/s,采用数值模拟的方式对原油携水流动特性进行计算是可行的。
2.2 流动特性分析
在流速0.12 m/s、积水量40 mL 条件下,对θ=30°和120°两种管壁润湿角的油水界面形态进行分析,取上倾管段100 mm 处的截面流速进行监测(图3)。在油水界面处的原油流速最大,管顶的流速最小,这是由于油水界面处受底部积水挤压和油水界面张力的作用,有效水力直径减小,流速增大;而靠近管顶的部位距离管底积水较远,受积水挤压效应的影响较小,同时受两相重力和管壁阻碍作用较为明显,因此从油水界面处到管顶的流速呈现不断降低的趋势。对比两种润湿角,θ=30°时积水沿管道径向和轴向扩散,积水平铺在上倾管段,呈分层波浪流型,积水厚度较小;θ=120°时积水积聚在上倾管肘部位置,呈水团状,水团呈明显波浪现象,积水厚度明显增加,水团的形成减少了管内的有效流通面积,原油流速变化较明显。
对比图3a 和图3b 可知,水相流速在靠近管底的位置均出现了负值,说明水相与壁面接触部分存在回流,这是由于管底受油水界面剪切应力的影响较小,此时油相具有的湍动能不足以克服油水之间的界面张力,无法阻止水滴的聚并和因重力作用导致的水滴沉降,当重力作用占主导时,水相开始沿壁面回流;在不断向下运动的过程中,水相厚度不断减小,有效水利直径增加,受到的油水界面剪切应力又不断增加,当剪切应力占主导时,水相再次攀升,形成循环过程。积水通过不断地回流和攀升往复运移流向出口,图4 为θ=30°、流速0.13 m/s、积水量40 mL 时的局部流型分析图。

图3 两种管壁润湿角下的油水界面形态Fig.3 Oil-water interface morphology under two wetting angles of pipe wall
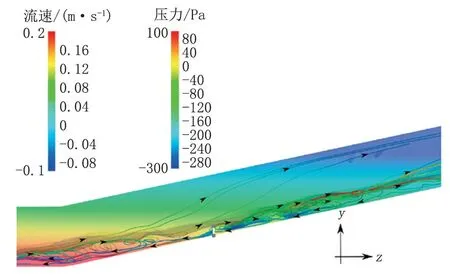
图4 局部流型分析图Fig.4 Analysis diagram of local flow pattern
2.3 壁面润湿性对携水流动的影响
在管道出口设置监测面,在积液量40 mL 条件下,对比不同原油流速下出口携水量变化(图5)。在同一流速下,原油携水量与时间呈线性关系,说明携水量基本保持恒定。随着流速增大,原油对油水界面的剪切应力不断增强,出口处的携水量不断增加。以图5a 为例,在管壁润湿角30°条件下,当原油流速为0.07 m/s 时,原油对积水表面的剪切力不足以克服重力作用,此时随着积水接近上倾管段,水平管段的水膜厚度逐渐增大,而上倾管段的水膜厚度逐渐变小,导致积水未到达管道出口;当原油流速超过0.11 m/s 时,积水随原油不断到达管道出口,且随着时间的延长,积水可全部流出,因此临界流速为0.11 m/s。对比两种接触角下的临界流速,θ=120°条件下的临界流速为0.08 m/s,较θ=30°时更小,这是由于积水形成的截面形状为水相体积和壁面润湿性的函数,θ=120°时界面失稳,积水在上倾管段形成了连续水团,较厚的水团占据了更大的管道直径,在原油流量恒定的条件下,因流速增加引发了较大的剪切力,因此较低的原油流速就能引发原油携水效应。
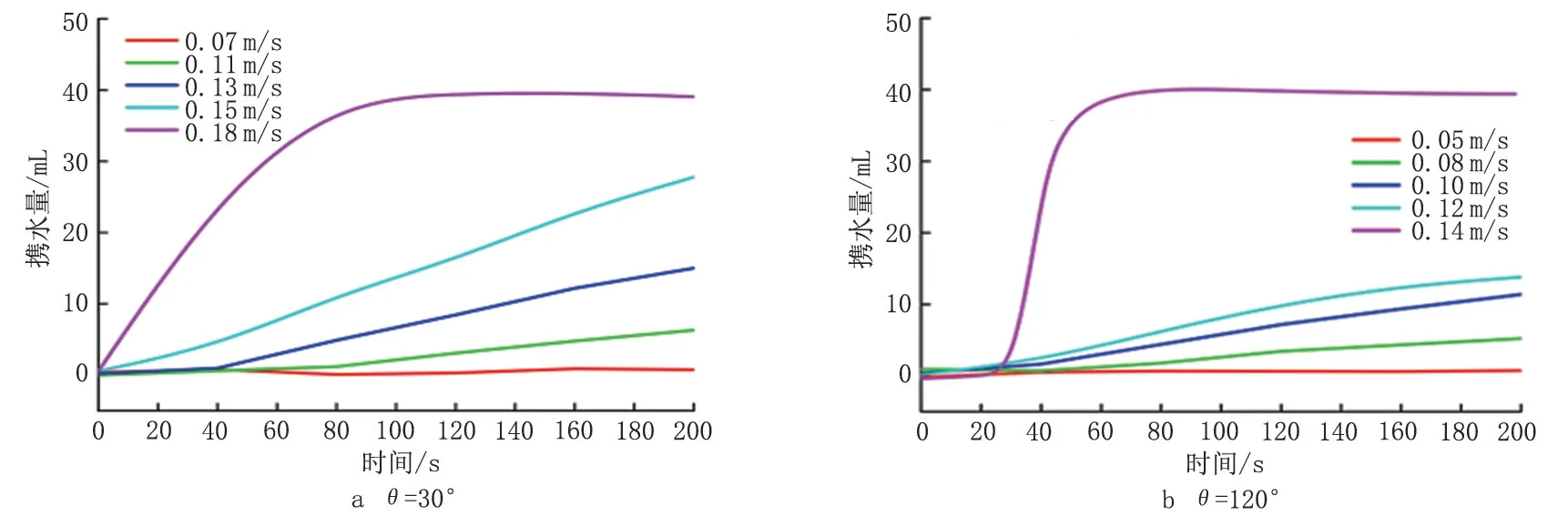
图5 不同原油流速下出口的携水量变化Fig.5 Variation of outlet water carrying volume at different crude oil flow rates
此外,在θ=30°条件下,当原油流速为0.18 m/s时,原油携带全部积水所需要的时间大幅减少,出现了明显的积水移动加速现象。这是由于在湍流混合的过程中,油水界面两侧切向速度差引发了开尔文-亥姆霍兹(Kelvin-Helmholtz)界面波动现象,导致界面处的剪切作用急剧增加,加快了积水的移动速度。在充分考虑黏性流体效应的前提下,Brauner 等[11-12]对油水两相流中的Kelvin-Helmholtz界面波动现象进行了研究,推导了积水移动加速公式:
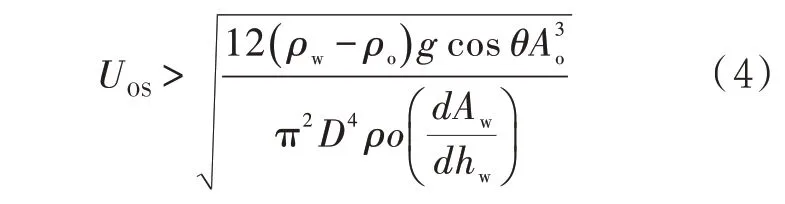
式中:UOS为原油流速,m/s;ρw、ρo分别为水相和油相密度,kg/m3;θ为管壁润湿角,°;Ao、Aw分别为油相和水相的表面积,m2;D为管道内径,m。
经计算,在θ=30°和120°的条件下,UOS分别为0.162 m/s和0.121 m/s,略低于模拟数值0.18 m/s和0.14 m/s,但总体与模拟结果相吻合。
原油流速对积水移动的影响体现在剪切作用力上,而壁面润湿性通过影响有效水力直径间接影响积水移动速度。为了进一步分析壁面润湿性对有效水力直径的影响,对上倾管段同一截面位置的水膜厚度比(水膜厚度hw与管道内径D的比值)进行模拟(图6),水膜厚度hw随润湿角θ的增大而增大。这是由于上倾段由分层波浪流转为水团流,与图3 结果相符。在θ=30°时,初始水膜厚度比随积液量的增加而增加,这是由于上倾管段存在弯曲部分,限制了积水的轴向和径向发展;在θ=120°时,底部积水的形状不确定,初始水膜厚度比与积液量无关,说明界面失稳情况更加严重,与之前的流型模拟结果相符。

图6 不同原油流速下的水膜厚度比Fig.6 Water film thickness ratio at different crude oil flow rates
3 结论
(1)采用Fluent 软件对原油携水模型进行数值模拟的方法切实可行,实验值和模拟值具有很好的一致性。
(2)随着原油流速和壁面润湿角的增大,原油携水能力逐渐增强。在θ=30°时,上倾管段呈分层波浪流;在θ=120°时,上倾管段呈水团流。原油临界流速的大小与壁面润湿性密切相关。
(3)当原油流速增大到一定值时,会出现Kelvin-Helmholtz 界面波动现象引发积水加速。
