改进遗传算法在辽东山区水文地质参数反演中的应用
2021-10-22孙颖
孙 颖
(盘山县农业水利事务服务中心, 辽宁 盘锦 124000)
水文地质参数是区域水文地质分析、水利工程勘察的重要设计参数[1]。水文地质参数主要获取的方法是基于野外勘察结合抽水试验,对勘察区域的相关水文地质参数进行分析[2]。这种方式的优点在于和勘察区域实际水文地质概况吻合度高,缺点在于不能实现区域水文地质参数分布的分析,只能针对采样点进行单一水文地质分析[3]。近些年来,基于野外勘察和抽水试验,建立水文地质参数样本数据系列和地质土层的相关模型进行反演的方法,可结合勘察区域地质分布情况,实现区域水文地质参数空间反演,在国内许多区域得到应用[4- 8]。这其中遗传算法由于可考虑样本数据系列的多个影响因素,在水文地质参数反演中应用较为普遍。但传统遗传算法由于不能考虑模型收敛度,存在无法收敛求解的情况,为此有学者对传统遗传算法进行改进,在多个研究成果应用中表明[9- 13],相比于传统遗传算法,改进的遗传算法可加速模型收敛求解,求解精度得到一定程度的提升,但改进遗传算法在区域水文地质参数中还未得到相关应用,辽东属于辽宁省典型的山区,为提高区域水文地质参数的反演精度,本文结合改进的遗传算法对区域水文地质参数进行反演分析,并结合抽水试验对反演水文地质参数进行验证分析,研究成果对于于辽东山区水文地质参数计算具有参考价值。
1 改进遗传算法原理
遗传算法针对各模型变量交叉概率的优化计算:
PC=PC1-(PC1-PC1)(fmax-f′)
(1)
式中,PC1—改进算法变量最优解;fmax—反演参数的最大取值;f′—反演参数的取值。
改进算法对各水文地质参数进行变异度的计算:
Pm=(Pm1-Pm2)(fmax-f′)
(2)
式中,Pm1—模型变量变异度最大值;Pm2—模型变量变异度最小值。
改进遗传算法针对各水文地质参数进行优化计算:
(3)
式中,dij—不同水文地质参数反演的样本间距;Si—样本数据系列最小值。
各样本数据间距计算方程为:
(4)
式中,Xi—渗透系数样本数据系列;Xj—储水系数样本数据系列。
对两个水文地质参数样本数据系列进行目标函数的计算:
f′(Xi)=f(Xi)/Si
(5)
式中,f(Xi)—目标函数适应度;f′(Xi)—改进后的目标函数适应度。
*θ表示为土层含水率(%);γ为土壤容重 (g/cm3);ω为土壤水饱和度(%);G为土壤给水度(%);T为地表温度(℃)
结合Holt-Winters对改进遗传算法进行目标函数的优化:
Yt+s=(Yt+GtS)Ht-L+S
(6)
式中,Yt+s—水文地质参数目标求解值;S—反演步长;Ht—不同时段调整度;Gt—变量趋势度。
对不同变量进行适应度的计算:
(7)
式中,M—样本数据系列总数;f—水文地质参数目标函数优化求解值;Qi—反演参数输出变量。
2 实例分析
2.1 区域概况
本文以本溪山区为具体实例,该区域主要由四个裂隙含水层所组成。各裂隙含水层主要水文地质参数见表1。结合抽水试验对不同含水层的储水系数以及渗透系数进行测定。
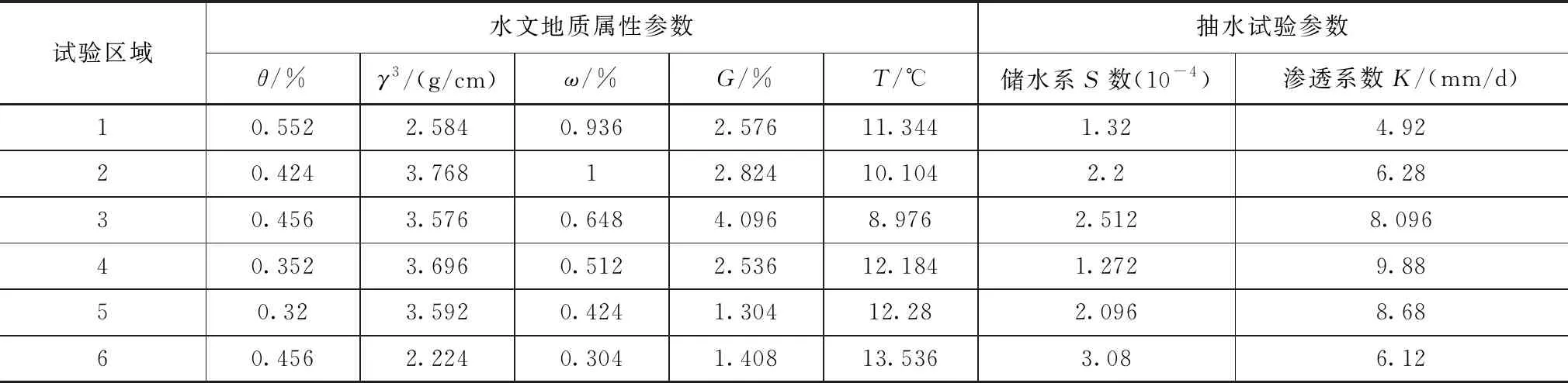
表1 不同含水层水文地质参数测定结果
2.2 模型检验
2.2.1T检验结果
改进遗传算法对不同水文地质参数反演进行优化求解,因此需要采样T检验对改进遗传算法进行不同水文地质参数和各含水层水文地质属性参数之间相关性进行检验,从而建立两组变量之间的关联度,检验结果见表2。

表2 改进遗传算法水文地质参数反演T检验结果
从改进遗传算法渗透系数和储水系数的lnθ影响因素下的T检验值高于4.0以上,储水系数的lnθ值要高于渗透系数,可见lnθ对储水系数影响程度要高于渗透系数。lnγ影响下的T检验值在0.029~0.105之间,满足T检验要求。干湿密度lnγ对于透系数和储水系数两个水文地质参数的影响程度较为接近。其他三个含水层变量的T检验值也均可满足90%的假设检验水平。从T检验值总体可看出,含水层的5个水文地质影响参数均和渗透系数和储水系数具有较好的关联度。
*lnθ为土层含水率极大似然估算参数;lnγ为土壤容重极大似然估算参数;lnω为土壤水饱和度极大似然估算参数;lnG为土壤给水度极大似然估算参数;lnT为地表温度极大似然估算参数;eT为地表温度极大似然估算参数
2.2.2F检验结果
采样F检验方法对改进遗传算法构建的水文地质输出变量和各含水层自变量参数进行非线性检验,结果见表3。

表3 水文地质输出变量和各含水层自变量参数的F检验结果
从分析结果可看出,渗透系数和储水系数两个水文地质参数和其他含水层自变量参数之间的F检验值在29.500~31.823之间,各自变量参数和两个水文地质参数之间的非线性变化程度较低,这主要是因为水文地质参数和各自变量参数之间具有较高的关联度所致。通过F0.05检验值分析渗透系数和储水系数两个水文地质参数和其他含水层自变量参数可满足95%的F0.05=2.124的显著性检验,表明两个水文地质参数和含水层物理属性参数存在显著的分析线性变化,可以用来构建回归方程,并结合改进遗传算法进行反演方程的求解计算。
2.3 参数反演验证结果
结合6个典型区域按照抽水试验对不同含水层的渗透系数和储水系数进行测定,并分别结合改进前后的遗传算法对水文地质参数进行反演,从而对参数反演值进行验证,验证对比结果见表4,并对不同方法反演的渗透系数和储水系数进行相关性分析,如图1所示。
从抽水试验对改进前后遗传算法下渗透系数和储水系数两个水文地质参数的反演验证结果可看出,相比于改进前,改进后的遗传算法由于加速求解的收敛度,使得渗透系数和储水系数两个水文地质参数与抽水试验测定值之间的相对误差平均降低15%左右。此外改进遗传算法不但可加速模型收敛度,还对渗透系数以及储水系数两个水文地质参数和含水层之间地质属性参数建立了映射和关联关系,使得模型构建的求解方程更符合区域实际含水层概况,因此改进遗传算法相比于传统遗传算法,在区域水文地质参数的反演精度更高。通过改进遗传算法,结合各含水层地质物理属性参数,即可对区域渗透系数和储水系数两个水文地质参数进行时空反演,从而获得区域水文地质参数的空间分布结果。从图1改进前后的遗传算法下渗透系数和储水系数参数和抽水试验测定参数的相关性分析结果可看出,相比于改进前遗传算法,改进后的遗传算法反演的渗透系数以及储水系数两个水文地质参数和抽水试验测定的水文地质参数值之间的相关度平均提高0.4左右,这主要是因为改进遗传算法建立的变量和自变量参数之间的关联度,提高了模型收敛精度,使得其反演值和试验测定值的相关性更高。

图1 改进前后的遗传算法下的渗透系数和储水系数参数和抽水试验测定参数的相关性分析结果
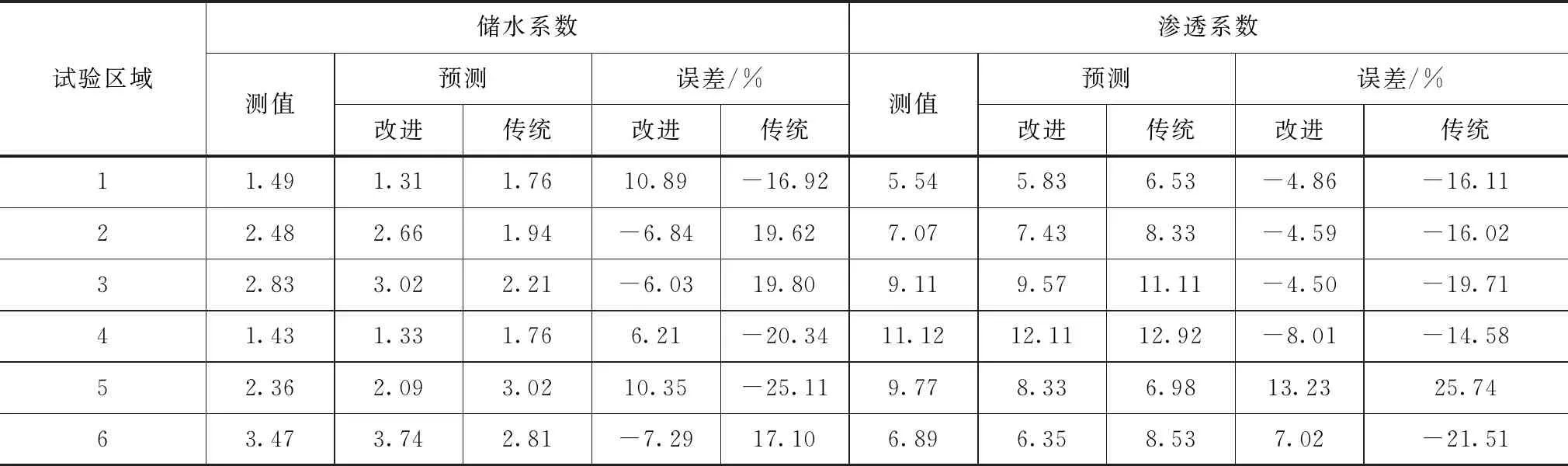
表4 不同含水层的渗透系数和储水系数参数反演验证结果
3 结论
(1)渗透系数和储水系数两个水文地质参数和其他含水层自变量参数之间的F检验值在29.500~31.823之间,各自变量参数和两个水文地质参数之间的非线性变化程度较低,这主要是因为水文地质参数和各自变量参数之间具有较高的关联度所致。
(2)渗透系数和储水系数两个水文地质参数和含水层物理属性参数存在显著的分析线性变化,可以用来构建回归方程,并结合改进遗传算法进行反演方程的求解计算。
(3)相比于改进前,改进后的遗传算法由于加速求解的收敛度,使得渗透系数和储水系数两个水文地质参数与抽水试验测定值之间的相对误差平均降低15%左右,且改进后的遗传算法反演的渗透系数以及储水系数两个水文地质参数和抽水试验测定的水文地质参数值之间的相关度平均也可提高0.4左右。
