单活塞线性压缩机用动力吸振器理论分析与Matlab仿真
2021-10-22孔德锐李海英
孔德锐,夏 明,李海英,陈 军,赵 鹏
〈制冷技术〉
单活塞线性压缩机用动力吸振器理论分析与Matlab仿真
孔德锐,夏 明,李海英,陈 军,赵 鹏
(昆明物理研究所,云南 昆明 650223)
单活塞线性斯特林制冷机由于其降温速度快、质量小和可靠性高等特点,目前正广泛用于红外探测器中,但是由于压缩机运行时产生的振动会严重影响探测器成像质量,所以在振动抑制方面动力吸振器的使用成为单活塞线性压缩机的最佳减振方式。基于此,本文首先论述了动力吸振器在单活塞线性压缩机减振方面的作用,并举例介绍了当前单活塞线性压缩机用动力吸振器的基本结构。为了不失理论分析的一般性,在动力吸振器与压缩机振动模型的理论计算中引入了几个重要的无量纲参数。最后在此基础上,利用Matlab软件对动力吸振器与压缩机模型进行振动幅频特性仿真。
单活塞线性压缩机;动力吸振器;理论设计;Matlab仿真
0 引言
随着低温电子器件和红外探测技术的升级换代,对斯特林制冷机提出了更高的应用需求。而在不同的应用条件下,对各类型斯特林制冷机的性能要求也有所不同。从表1[1]可以看出,单活塞线性斯特林制冷机虽然在降温时间及可靠性方面有良好的表现,但由于压缩机较大的振动输出会直接影响到探测器的成像质量。因此有效地减小压缩机的振动,成为提高单活塞线性斯特林制冷机性能的关键。
目前,对于单活塞线性压缩机的减振主要采用被动减振技术。原因在于被动减振系统具有结构简单、可靠性高和不耗电能等优点,且当压缩机在固定工作频率下运行时,减振效果明显。而随着被动减振技术中动力吸振器的发展,国外许多研发机构在消减单活塞线性压缩机振动方面成效显著,这使得它们进一步将单活塞线性压缩机采用隔振安装后,其振动输出已经能达到国际空间0.2N的微振动要求[2]。例如:AIM公司SX030动磁式压缩机和RICOR公司的K527动磁式压缩机在使用上述的减振技术后,其输出的振动值均小于0.2N,表2[3-4]是两种不同制冷机用单活塞线性压缩机适配动力吸振器并采用隔振安装后的相关参数。从表中数据还可以看出,RICOR/K527压缩机仅仅采用隔振安装后,其振动数值仍然较大,而当适配动力吸振器后,在相同输入功率下,输出的振动仅为30mN。由此可见,在单活塞线性压缩机减振技术方面,动力吸振器有着巨大的作用。

表1 不同类型斯特林制冷机技术特点[1]
表1中对应参数的√越多,表示制冷机在此方面具有更好的优势。例如,对于单活塞线性斯特林制冷机(split linear single piston)而言,其降温时间(cooling time)和平均失效前时间(MTTF)均比旋转集成式(integral rotary)更有优势,但其集成度(integration)不如旋转集成式的高,输出的振动(vibration)也相对较大。
1 单活塞线性压缩机振动分析
在对动力吸振器设计前,需了解被减振物体的振动成因。单活塞线性压缩机的振动来源主要是活塞运动时产生的不平衡力,而这也是由于其独特的驱动结构。这种压缩机是利用结构中电磁力、弹力和阻尼力组成的机械共振系统推动压缩活塞往复运动[5-6]。在此技术上,按照电磁驱动方式,主要可分为动圈式和动磁式两种。因为在对两种驱动方式进行振动分析时是一致的,所以本文仅以动磁式单活塞线性压缩机为例。
1.1 动磁式单活塞压缩机介绍
动磁式压缩机是在动圈式电磁驱动技术上进一步发展而来的。图1是动磁式单活塞压缩机结构图,(a)为压缩机结构示意图;(b)为RICOR公司K527单活塞动磁式压缩机剖面图[7]。径向磁化环(radially magnetized ring)产生的永久磁场与驱动线圈(driving coil)产生的交变电磁场相互作用产生轴向洛伦兹力,并施加在磁环和由内外磁轭(internal yoke, external yoke)及驱动线圈形成的定子上。由于磁环被粘合在磁钢支架上,该磁钢支架又刚性地联接于压缩活塞(compressor piston)上,就可以推动压缩活塞在气缸套内自由往复运动。
1.2 振动分析
对以上压缩机结构进行振动分析时,可以简化为如图2所示的振动模型。径向充磁的永久磁铁处于内外磁轭构成的气隙中,当励磁线圈中通过交流电时,气隙中形成交变气隙磁场,永磁体受到交变的电磁力,从而推动电动机活塞组件往复运动。期间,通电线圈也同样受到交变电磁力的作用,而由于线圈是紧密缠绕在与定子组件固连的支架上,所以交变的电磁力也同时作用于定子组件。因此,驱动力()(电磁力)不仅作用于活塞组件1,更作用于压缩机定子组件(线圈、线圈支架、气缸、内外磁轭、压缩机外壳)2上。所以当压缩机在运行时,压缩机定子组件也会因活塞组件运动而产生振动力()。
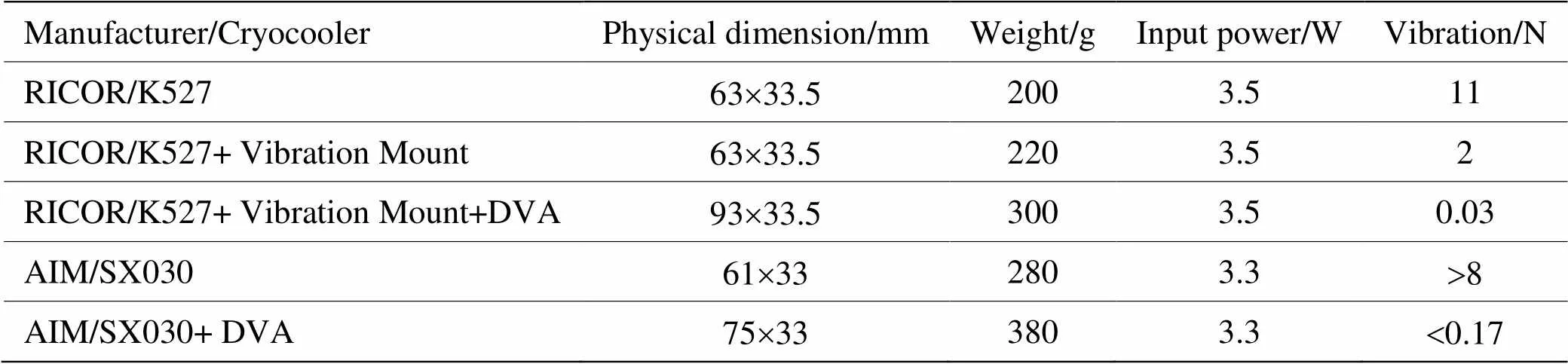
表2 K527和SX030压缩机相关参数
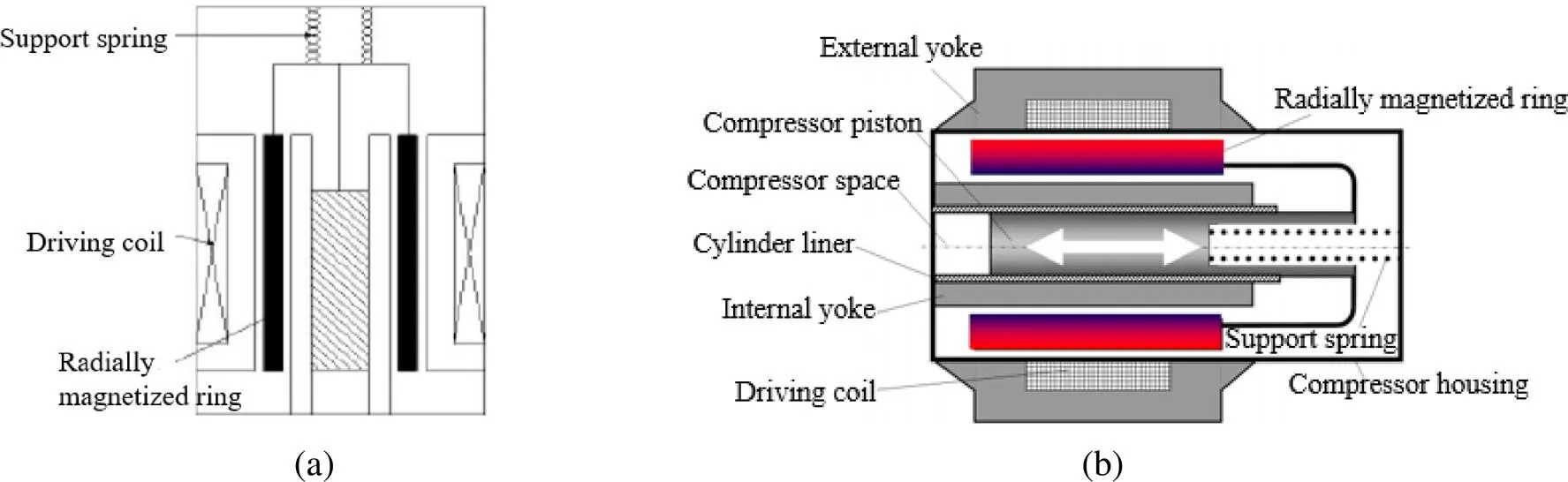
图1 动磁式单活塞压缩机结构示意图(a)和剖面图(b)
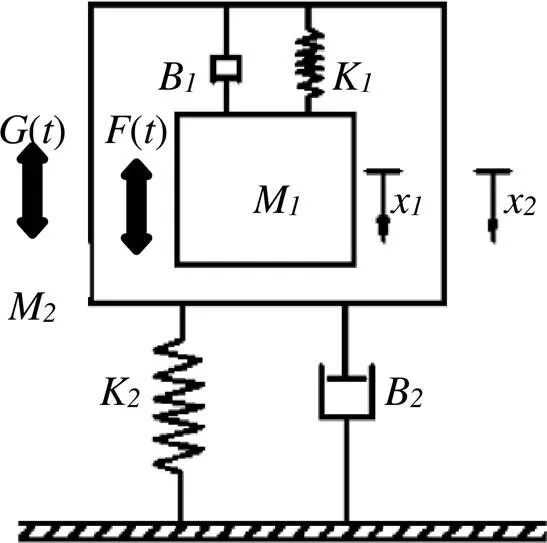
图2 单活塞压缩机振动示意图
从压缩机输出的振动力()是影响系统其他集成组件稳定运行的重要因素,因此利用动力吸振器的运动来消减压缩机本身的振动输出,并抑制振动的传输成为提高制冷机及其他系统组件工作性能的关键措施。
2 动力吸振器基本结构
常见的单活塞压缩机用动力吸振器主要包括板簧和配重两大部分,通过调节两部分之间的参数关系,即通过设计吸振器板弹簧数量、厚度和线型得到最佳的等效刚度,以及调节配重质量,就可得到适配压缩机工作频率的固有频率。
图3[3]为AIM公司动力吸振器结构图(a)和适配SX030压缩机装配图(b),其结构采用两片板弹簧和两个配重块,并通过中心孔固定的方式装配并连接于压缩机。
RICOR公司A. Veprik等人一直从事斯特林制冷机减振技术的研究。其中最具代表的就是K527制冷机用动力吸振器的研究。图4[4,8]分别为K527制冷机动力吸振器结构图(a)和实物图(b)。
Sunpower公司同轴型单活塞斯特林制冷机也是采用动力吸振器进行减振。从图5可以看出,其动力吸振器仍是通过中心孔将两片板弹簧及配重连接于压缩机[9]。
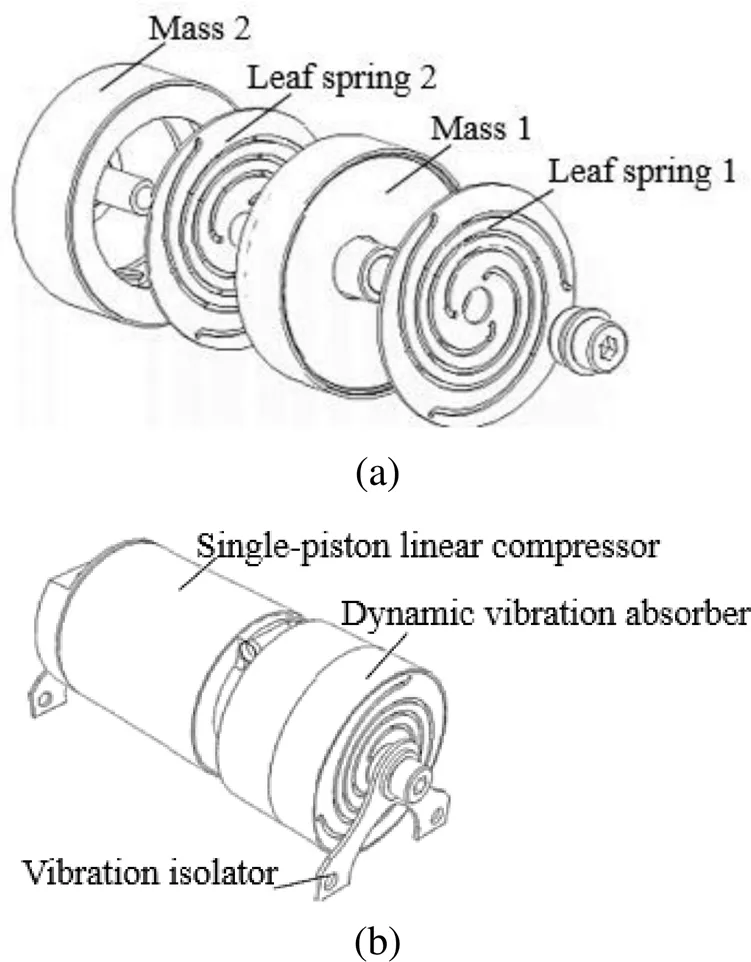
图3 SX030压缩机用动力吸振器爆炸图(a),装配图(b)

图4 K527制冷机用动力吸振器爆炸图(a),实物图(b)

图5 Sunpower制冷机与动力吸振器装配实图
3 动力吸振器设计
3.1 建立振动模型
如图6所示,采用动力吸振这种被动减振技术时,吸振器将通过一定的方式与压缩机连接,其振动模型见图7。

图6 装配动力吸振器的单活塞线性压缩机
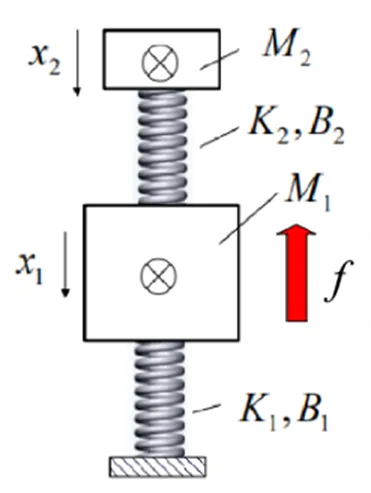
图7 振动模型
在对这种结构的吸振器进行振动分析时,由于吸振器从外观上判断不属于压缩机部分,所以可将压缩机视为一个质量单元,其内部的气体力可以不参与振动分析。因此模型中的1并不只是运动活塞质量,而是压缩机总质量;1、1则是压缩机安装于隔振支座时的等效刚度和阻尼;为压缩机因活塞组件运动产生的振动力。在吸振器部分,2代表吸振器质量,2为板簧刚度,2为吸振器等效阻尼(由于在吸振器中阻尼力<<弹性力,所以可近似认为2=0)。
由此可建立模型振动微分方程:
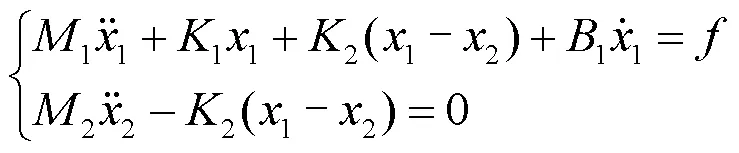
引入傅里叶变换,得到相关傅里叶变换参数:
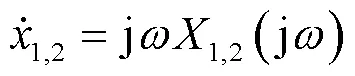
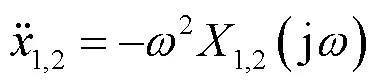
傅里叶变换后可得:
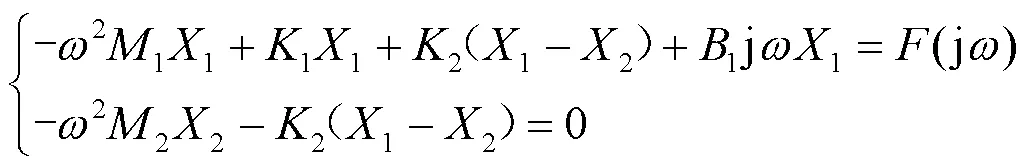
由(2)得:
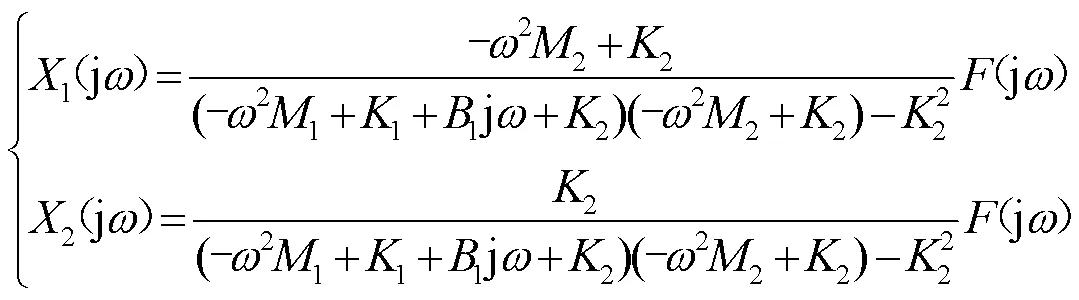
从上式可以知道,当吸振器固有频率等于压缩机工作频率时,即(2/2)1/2=,压缩机输出的振动位移值理论上可趋近零,即1(j)≈0。但由于吸振器自身存在结构阻尼和其他阻尼的影响,会导致压缩机输出的振动位移值存在一个下限,所以在这种情况下,尽管吸振器阻尼力远小于弹性力,但受阻尼的影响不可忽视。考虑吸振器阻尼后,系统振动微分方程则为:
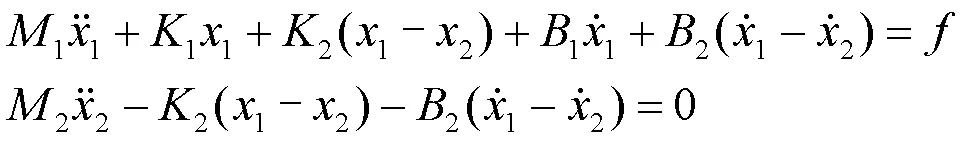
经傅里叶变换后:
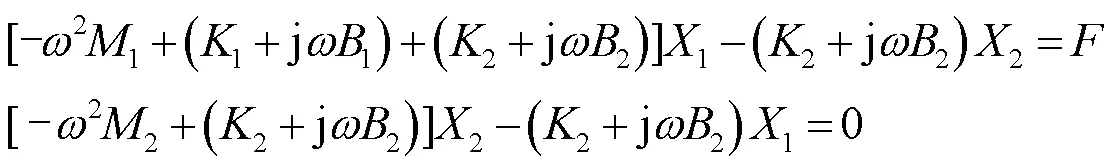
由式(5)可得:
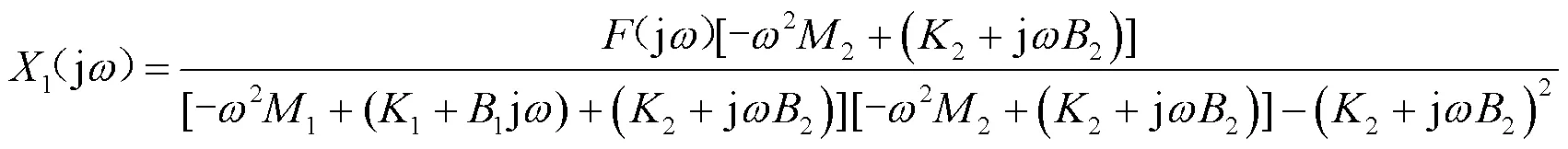
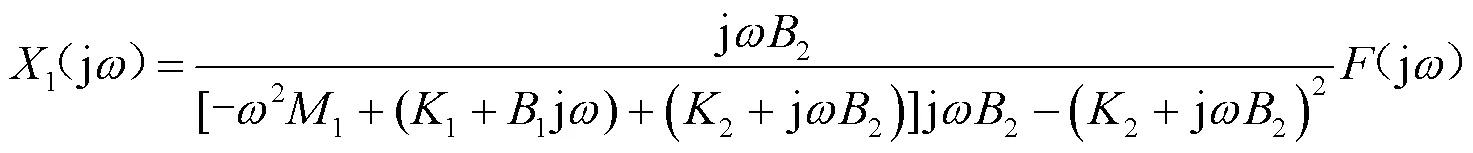
通常压缩机安装于阻尼较小的柔性隔振器(1≈0)[10]。则由式(6)可得:
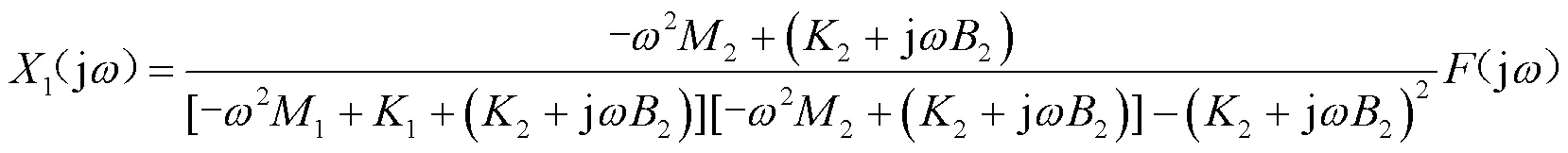
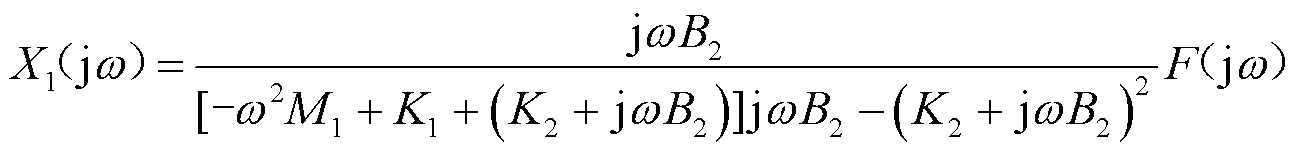
引入无量纲参数:
=2/1-质量比=吸振器质量/压缩机质量
1=(1/1)1/2-压缩机质量固有频率
2=(2/2)1/2-吸振器固有频率
=2/1-固有频率比
=/1-激励频率比
2=2/[2(22)1/2]-阻尼比
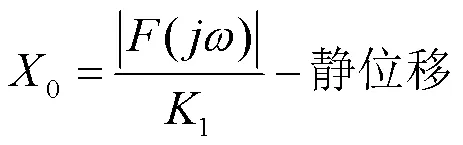
由此可得到:
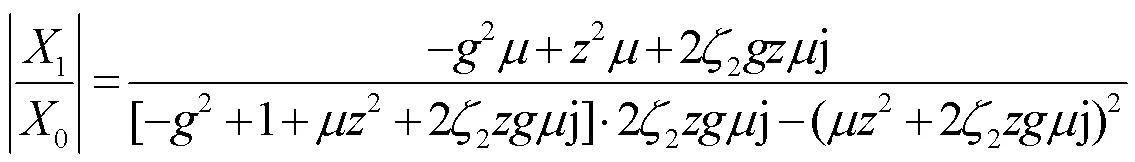
从上述分析可知,吸振器是根据某一特定频率设计的,所以作为单频减振器,其减振效果会受频率变化的影响。本案例中,假设压缩机工作频率为75Hz,而在压缩机未使用吸振器之前,仅会在工作频率或附近出现一个共振点。当使用吸振器后,虽然压缩机在工作频率点会出现“反共振”,即振动最小点,但同时在其左右会产生两个新的共振点[11],见图8的Matlab仿真曲线。

图8 压缩机使用动力吸振器前(a)后(b)振动曲线
由式(10)可知,压缩机的振幅是,,和2的函数,激励频率比又体现在压缩机主质量固有频率上,因此吸振器的减振效果主要与,和2有关。图9是当=1、=1/10,压缩机在不同的2值下,对应的振幅与频率的幅频特性曲线。
从图9中可以看出,当2=+∞时,压缩机和吸振器相当于固结在一起,系统类似于一个质量为1+2,刚度为1的单自由度系统,从而使压缩机在工作频率75Hz处无法达到反共振状态。
3.2 压缩机幅频特性与m的关系
从前文分析可知,虽然不能避免压缩机在启动和停止时经过第一个共振点,但在吸振器设计中应该注意两个共振点尽可能远离工作频率。图10为=1、2=0.12时,不同值的Matlab仿真曲线,从图中可知,两个共振点的频率带宽与平衡块质量有密切关系,往往平衡块质量越大两个共振点离“反共振”点越远。
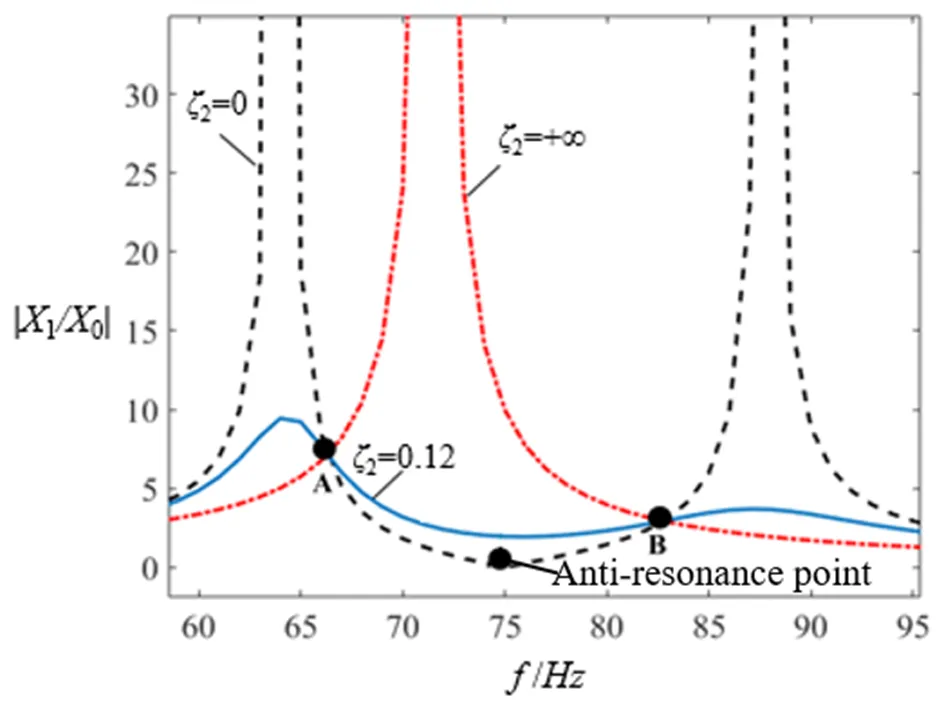
图9 压缩机幅频特性曲线
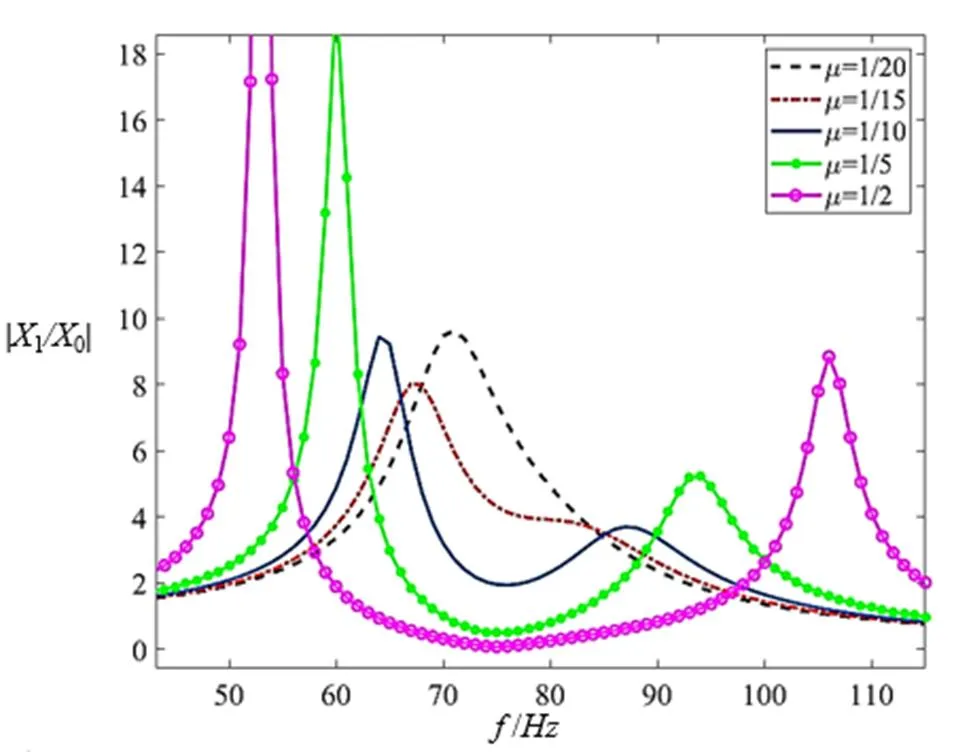
图10 不同m值对应的压缩机幅频特性Matlab仿真曲线
通常吸振器质量与压缩机质量比取10%~20%,即值在1/10~1/5之间[12]。因为吸振器质量过大,虽然两个共振点离“反共振”点越远,但两共振峰值,尤其是低频处峰值会变大。
3.3 压缩机幅频特性与z的关系
从图6可以看出,阻尼比从0~+∞的曲线都会在、两点相交,可以将2=0和+∞两临界条件代入式(10),即可确定两点位置。
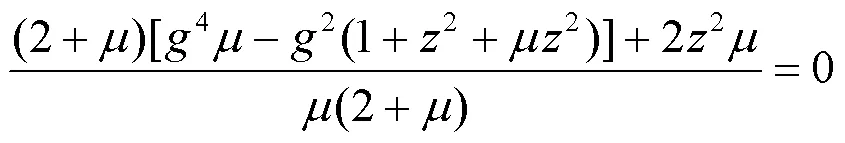
式(11)的两根12、22即对应着、处的频率比g和g,换而言之对应着、两点的频率。将计算得到的g和g代入式(10)即可得到、的纵坐标,而当两点纵坐标相等时吸振器减振效果最好[13],此时有:

当=1/10,2=0.12时压缩机幅频特性曲线与的关系如图11所示。
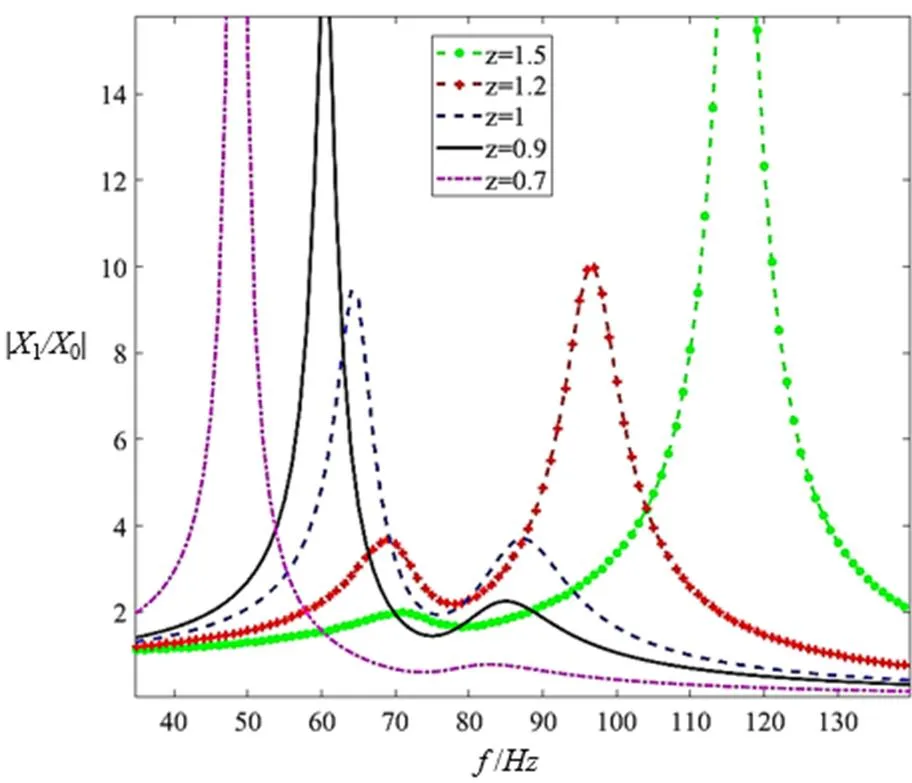
图11 不同z值对应的压缩机幅频特性Matlab仿真曲线
从图11可以看出,随着值的减小,压缩机工作频率75Hz处的反共振点值减小。此外,在图中还可以看出以下几个特性:
1)当吸振器固有频率大于压缩机主质量固有频率,即>1时,最大共振峰值位于“反共振点”的右侧。当吸振器固有频率小于压缩机主质量固有频率,即<1时,最大共振峰值位于“反共振点”的左侧;
2)虽然在=1的情况下,左右两处共振峰值最小,但反共振点处数值较高;
3)当=0.7时,虽然反共振点的值最小,但左侧共振峰值却最大。
因此在本案例中,当满足式(12)的要求,即=1/10,=0.9时,即控制了右侧最大共振峰值,又满足压缩机在反共振点处具有较小的振动值。由此可见,要达到这种要求,压缩机与隔振器之间不能存在刚性安装,需调节压缩机安装的隔振器刚度1,从而使吸振器的固有频率与安装于隔振器后的压缩机固有频率比尽可能接近理论值。例如:图12为RICOR公司柔性隔振器的设计,这种设计一方面可以抑制压缩机的振动输出,另一方面隔振器中弹性导热材料的使用,可以为压缩机提供很好的散热性能[4,14]。
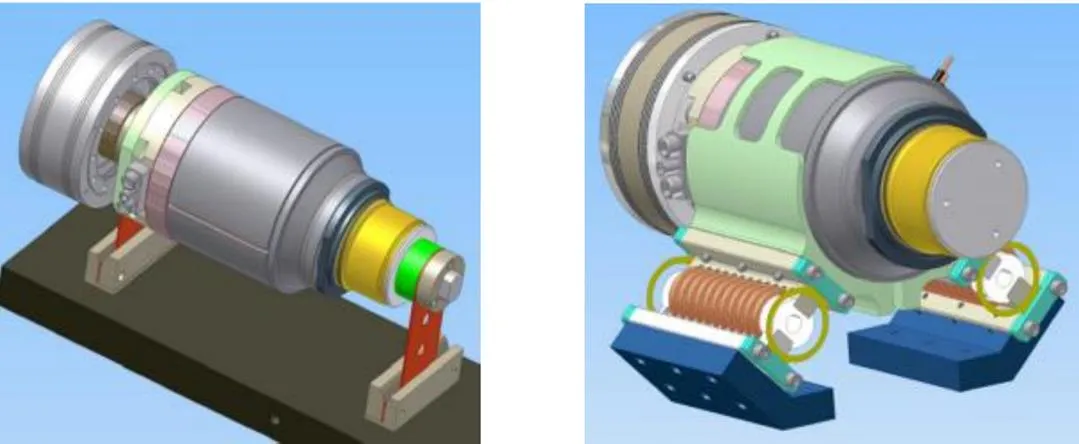
图12 RICOR公司外部柔性板弹簧隔振器(a)、螺旋弹簧隔振器(b)
3.4 压缩机幅频特性与z2的关系
尽管在对吸振器2、2参数设计时,可以假设2≈0,从而根据公式222=2来初步设计吸振器质量和所需刚度。但吸振器因自身结构特性即运行时的环境因素等影响会存在一定的阻尼。从图9可知,吸振器的阻尼并不是越小越好,而是存在一个最优值。原因在于吸振器阻尼过小会在左右共振频率处出现峰值的突增。所以,除了保证压缩机在反共振点处的数值较小外,还要尽可能地使其在工作时经过左右共振点处的振动数值尽可能的平缓。
由上分析可知,在计算最优的2值时,可以先将式(12)代入式(11),简化后对频率求导,并令左右共振峰值处的斜率为零,可得:
左处共振点:
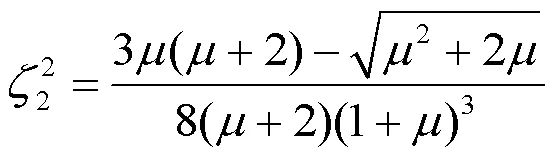
右处共振点:
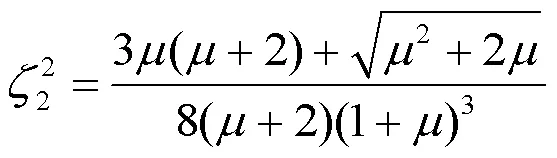
设计则可取上两式的平均值:
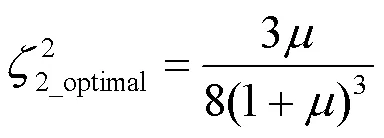
当=1/10,=1/(1+),压缩机幅频特性曲线与2的关系如图13所示。
从Matlab仿真曲线中可以看出,随着吸振器阻尼比2的增大,在反共振点处的减振效果越差。当吸振器大于最优设计值2_optimal时,压缩机在工作频率处基本无法达到反共振状态。而当阻尼比小于最优设计值2_optimal时,在接近左右共振点时,曲线斜率越大。
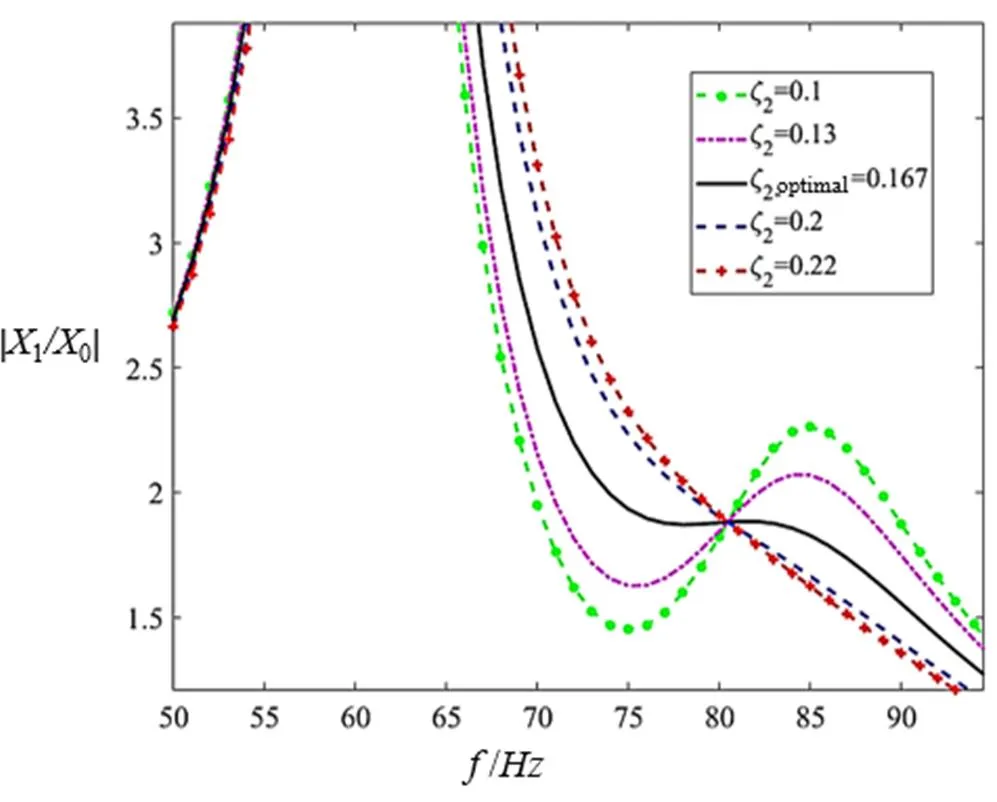
图13 不同z2值对应的压缩机幅频特性Matlab仿真曲线
4 总结与下一步研究计划
单活塞线性压缩机通过适配动力吸振器后,可以使其在工作频率处达到反共振状态,使振动输出大幅度减小,从而减小对斯特林制冷机及其他探测器组件的影响。尽管动力吸振器是一种极为可靠的被动减振技术,但在设计时仍要对其重要参数进行优化选择。本文通过对动力吸振器与压缩机模型进行振动分析,并利用Matlab进行不同参数下的幅频特性仿真后,得出以下几个结论。
1)动力吸振器的质量与压缩机质量比约为10%~20%,吸振器质量越小会使两共振频率离压缩机工作频率越近,且在工作频率处的反共振状态越弱;而吸振器质量过大,虽然可以使压缩机在工作频率处达到更好的反共振,但两共振峰也随着变大。
2)通过文中案例及分析可知,压缩机安装时要尽量满足式(12)关系,即安装于具有一定刚度的柔性隔振器。通常可以通过选择较低的隔振器弹簧刚度来达到进一步抑制压缩机振动传递到平台或其他集成组件的目的。
3)动力吸振器的阻尼比2存在一个理论上的限值,即公式(15)所述的最大理论值。在设计过程中如果大于这个理论值,将减弱动力吸振器在压缩机工作频率处的减振效果。此外,当阻尼比2过大时,压缩机和动力吸振器类似于刚性连接,从而使得动力吸振器无法发挥反共振的作用。
虽然通过本文关于动力吸振器完整的理论分析和实验仿真能较为清楚地知道在对其进行理论设计时需控制的参数范围。但在实际过程中由于材料性能、加工及装配等因素的影响,可能会使板弹簧及动力吸振器的刚度线性难以精确控制,从而在一定程度上会使动力吸振器偏离最佳设计工况点。基于此,在后续工作中将会对实物进行试验,并分析哪些实际因素会影响动力吸振器的减振性能。
[1] Katz A , Segal V , Filis A , et al. RICOR's Cryocoolers development and optimization for HOT IR detectors[C]//,+, International Society for Optics and Photonics, 2012, 8353: 83531U.
[2] 杨宝玉, 吴亦农. 空间机械制冷机的振动控制研究进展[C]//第八届全国低温工程大会暨中国航天低温专业信息网2007年度学术交流会论文集, 2007: 6.
YANG Baoyu, WU Yinong. Research progress of vibration control of space mechanical refrigerator[C]//8th2007, 2007: 6.
[3] RühlichI, Mai M, Rosenhagen C, et al. Compact high efficiency linear cryocooler in single piston moving magnet design for HOT detectors[C]//, 2012, 8353: 83531T.
[4] Veprik A, Zechtzer S, Pundak N. Split Stirling linear cryogenic cooler for a new generation of high temperature infrared imagers[C]//, 2010: 7660.
[5] 金涛, 郑水英, 谢洁飞, 等. 直线压缩机的研究现状与发展[J]. 中国机械工程, 2004, 15(8): 1405-1409.
JIN Tao, ZHENG Shuiying, XIE Jiefei. Research status and development of linear compressors[J]., 2004, 15(8): 1405-1409.
[6] 邰晓亮. 动磁式直线电机驱动微小型活塞压缩机理论分析及实验研究[D]. 上海: 上海交通大学, 2009.
TAI Xiaoliang. Theoretical analysis and experimental study of a miniature piston compressor driven by a moving magnet linear motor[D]. Shanghai: Shanghai Jiaotong University, 2009.
[7] Veprik A, Vilenchik H, Riabzev S, et al. Microminiature linear split Stirling cryogenic cooler for portable infrared imagers[C]//, 2007, 6542: 65422F.
[8] Sergey Riabzev, Ilan Nachman, Eli Levin, et al. RICOR K527 highly reliable linear cooler: applications and model overview[C]//, 2017, 1080: G1-G17.
[9] Sunpower. Cryocoolers Overview[EB/OL]. [2020-12-28]. https://www. sunpowerinc.com/products/stirling-cryocoolers.
[10] Veprik A M, Babitsky V I, Pundak N, et al. Vibration control of linear split Stirling cryogenic cooler for airborne infrared application[J]., 2000, 7(6): 363-379.
[11] 孙述泽, 闫春杰. 动力吸振器在斯特林制冷机振动控制中的应用[J].低温与超导, 2011, 39(6): 13-15, 57.
SUN Shuze, YAN Chunjie. Application of dynamic vibration absorber in vibration control of Stirling refrigerator[J]., 2011, 39(6): 13-15, 57.
[12] Kopasakis, George, Cairelli, et al. Adaptive vibration reduction controls for a cryocooler with a passive balancer[J]., 2002, 613(1): 1605.
[13] Ormondroyd J, Den Hartog J P. The theory of the dynamic vibration absorber[J], 1928, 50: 241.
[14] Veprik A, Zechtzer S, Pundak N, et al. Low vibration microminiature split Stirling cryogenic cooler for infrared aerospace applications[C]//,2011, 1434: 1473-1480.
Theoretical Analysis and Matlab Simulation of Dynamic Vibration Absorber for Single-Piston Linear Compressor
KONG Derui,XIA Ming,LI Haiying,CHEN Jun,ZHAO Peng
(Kunming Institute of Physics, Kunming 650223, China)
Single-piston linear Stirling cryocoolersare widely used in infrared detectors owing to their fast cooling, lightweight, and high reliability. However, the vibration generated by the compressor during operation considerably affects the imaging quality of the detector. Therefore, the use of a dynamic vibration absorber has become the best vibration reduction method for single-piston linear compressors. First, this article discusses the role of a dynamic vibration absorber in damping single-piston linear compressors and provides an example of the basic structure of current single-piston linear compressors.Second, togeneralizethe theoretical analysis, several important dimensionless parameters are introduced in the theoretical calculation of the dynamic vibration absorber and compressor vibration model.Finally, Matlab is used to simulate the vibration amplitude-frequency characteristics of the dynamic vibration absorber and compressor model
single-piston linear compressor, dynamic vibration absorber, theoretical design, Matlab simulation
TB652
A
1001-8891(2021)10-1014-08
2020-12-28;
2021-08-11.
孔德锐(1993-),男,云南昭通人,硕士研究生,研究方向:小型低温制冷机。E-mail:1024197919@qq.com。
夏明(1977-),男,研究员,主要从事小型低温制冷机研究。E-mail:15969586435@163.com。
