巧方法破解，多角度拓展——一道最值问题的探究

甘肃省靖远县第一中学 (730600) 唐旭尧

双变量或多变量关系条件下的代数式最值问题的求解，是近年高考中一个非常熟悉的“面孔”，经常在高考试卷中出现.此类问题变量众多，问题背景设置创新新颖，随着变量的系数、次数、符号、代数表达式等的变化，面目全非，变化多端，可以有效交汇不等式、函数或方程、导数以及其他相关的知识，融合数学知识、数学思想方法与数学能力等，能很好考查学生的数学能力，具有很好的选拔性与区分度，倍受命题者青睐.

1.问题呈现

问题(清华大学中学生标准学术能力诊断性测试2021年3月测试理科数学试卷·12)已知实数a，b，c满足a+b+c=1，a2+b2+c2=1，则a3+b3+c3的最小值是( ).

此题以“三元之和为1”与“三元平方和为1”为已知条件，进而确定“三元立方和的最小值”，创新新颖，问题背景具有渐进性、层次性，极具美感.破解问题的关键是巧妙借助对应公式的变形与转化，结合二次函数的性质、基本不等式、利用导数研究函数的单调性以及由函数的单调性确定函数的最值等知识的应用，巧妙融合，合理交汇，综合应用.

2.问题破解

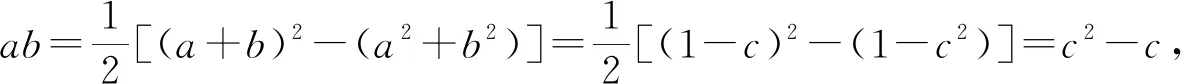
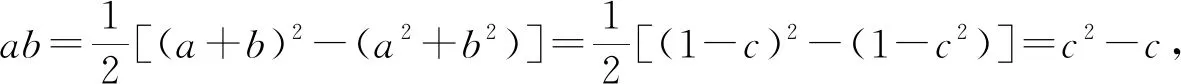
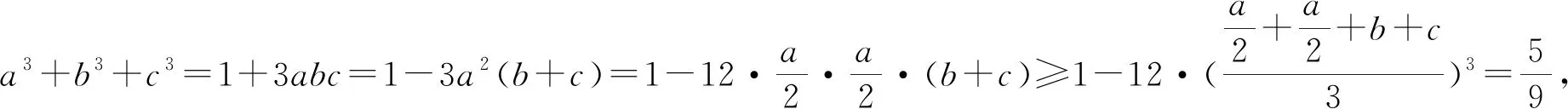
点评：合理通过代数关系式的变形与转化，巧妙配凑，把三元立方和转化为三元乘积，再通过关系式的变形，调配系数，利用三元均值不等式来转化与应用，进而得以确定对应的最值问题.不等式问题利用不等式思维来处理，是破解问题的常见思维，但对代数关系式的变形与配凑技巧性非常强，要求具备非常高的代数运算技巧与能力.

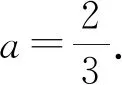
点评：极端思维方法处理，是借助多变元函数取最值时一般满足的条件来特殊情况切入，是一种逆推思维方式，有时不具有完备性.在解答选择题时可以结合选项的结论有选择性应用，而填空题等问题时要注意慎用.

3.变式拓展

探究1保留题目条件，改求“a+b的取值范围”，降低题目难度，得到以下变式问题.

变式1 已知实数a，b，c满足a+b+c=1，a2+b2+c2=1，则a+b的取值范围是( ).

A.[-1，1] B.[-，0] C.[0，] D.[0，2]

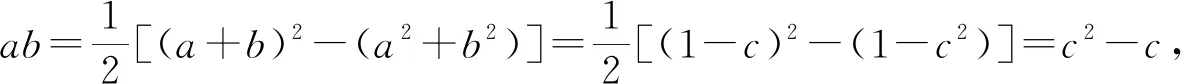
探究2保留题目条件，改求“a3+b3+c3的最大值”问题，得到以下变式问题.

变式2 已知实数a，b，c满足a+b+c=1，a2+b2+c2=1，则a3+b3+c3的最大值是( ).

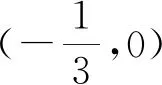
4.解后反思

破解双变量或多变量的关系条件下的代数式最值问题，关键是借助已知条件中的关系式，合理恒等变形，巧妙运算转化，充分深入理解，挖掘本质，合理整合，巧妙应用，结合不等式、函数或方程、导数以及其他相关的知识来分析与处理.同时，对于此类问题，要合理挖掘其丰富内涵，不断探究反思，举一反三，灵活变通，学会变式拓展，探究提升，真正达到融会贯通，从数学知识、数学能力、数学思维等层面融合，形成数学知识体系，转变为数学能力，有效应用于相应的数学解题，真正形成良好的数学品质，有效提高数学能力，培养数学核心素养.