控制方向未知的非线性系统有限时间跟踪控制
2021-10-22刘文慧
孟 波,刘文慧
(南京师范大学南瑞电气与自动化学院,江苏 南京 210023)
近年来,非线性系统有限时间稳定控制问题受到了国内外学者广泛的关注. 从工程实践的角度来看,有限时间稳定性比渐近时间稳定性更有意义,比如行驶中的汽车制动问题. 线性系统的有限时间控制问题是由Tang[1]所提出,该方法是更优于线性滑膜方法的终端滑膜方法. Lyapunov有限时间稳定性理论很好地解决了在非线性系统中由滑模控制器引起的抖振问题[2]. 近年来,Lyapunov有限时间稳定性理论的应用愈发广泛[3-6]. Li等[7]对一类多输入多输出的非严格反馈非线性系统结合反步法和动态面控制设计了有限时间控制器. 在现实生活中,船只航向、航空航天等的自动控制问题广泛涉及到控制方向未知的非线性系统,但是上述文献[3-7]并没有讨论当非线性系统控制方向未知时的控制问题. 在这一领域具有开拓性意义的是Nussbaum[8]提出的利用Nussbaum函数解决控制方向未知这一难题的方法,该方法至今仍是解决控制方向未知问题的主要方法. 文献[9-10]都是通过坐标变换将原系统转换为控制增益已知的新系统后设计了状态观测器应用Nussbaum函数和反步法来设计控制器,所不同的是前者设计的是线性观测器而后者设计的是模糊状态观测器. 文献[11-12]都利用了Nussbaum函数和动态面控制思想分别解决了系统控制增益符号未知的问题以及“计算膨胀”现象. 但是上述文献[8-12]并没有考虑有关控制方向未知的非线性系统的有限时间控制问题.
鉴于此,Ma等[13]针对一类具有执行器故障和未知控制方向的非线性系统设计了控制器,并且可以保证该系统全局有限时间镇定. Wu等[14]针对多未知控制方向的非线性系统提出了一种全局有限时间控制策略,文献[15]在文献[14]的基础上对于多未知控制方向非线性系统增加了未知参数并设计了全局有限时间控制器. 但是上述文献[12-15]都基于系统状态向量可测情形. 另一方面,作为控制系统中常见的非线性问题,死区往往会降低系统的控制性能,甚至导致控制系统的不稳定[16-19].
对于一类控制方向未知的不确定非线性系统的有限时间自适应输出反馈跟踪控制问题,本文主要做以下工作:
(1)针对文献[3-7]中系统均为控制方向已知,本文假设系统控制方向未知并借助Nussbaum函数来解决.
(2)对比文献[8-12]没有考虑有关控制方向未知的非线性系统的有限时间控制问题,本文对于此类系统设计了一种新的有限时间控制器.
(3)对于文献[12-15]的控制器是基于系统状态反馈设计的,本文对此条件进行了放宽,以此提出的控制策略可以更广泛地应用于工程实践.
1 问题描述、预备知识和模糊逻辑系统
1.1 问题描述
考虑下面严格反馈非线性系统:
(1)

(2)

H(υ)=μ(t)υ+Δ(t).
(3)
式中
然后可以得到:
(4)

假设2参考信号yr和它的n阶导数均是分段连续,已知且有界的.
1.2 预备知识

引理2[20]对于任意的正常数μ,τ,κ和实变量e,有不等式|e|μ||τ成立.

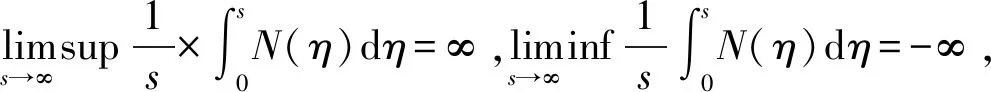
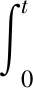
1.3 模糊逻辑系统
系统中的未知非线性项用模糊逻辑系统描述如下,IF-THEN规则:


2 模糊状态观测器设计
(5)
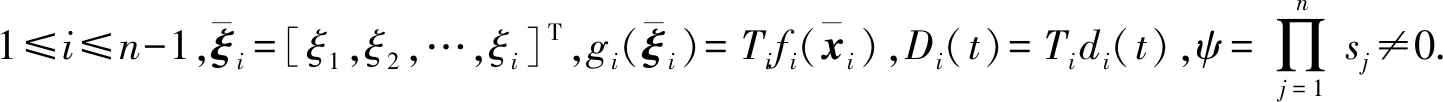

(6)
式中

(7)

(8)
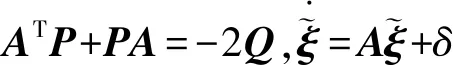
(9)
注1可以看到在系统(5)中,所有的控制增益都是已知的. 由于(5)由原系统(1)通过线性变换所得,所以(5)中所有的状态都是不可知的. 因此,本文设计了一个模糊状态观测器来估计(5)中不可测的状态,然后基于此观测器提出了一种新的有限时间控制策略.
3 控制器设计和稳定性分析
3.1 控制器设计
提出一种基于反步法的自适应有限时间控制方案. 跟踪误差zi以及Lyapunov函数分别为:
z1=y-yr,
(10)
(11)
(12)

第1步:由(5)、(10)计算跟踪误差导数为下式,其中ε′1=ε1+D1,
(13)
由(12)、(13)计算V1的导数为:
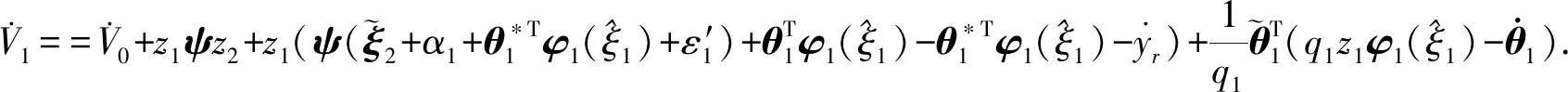
(14)
(15)
(16)
将(15)、(16)代入(14)可得:

(17)

(18)
(19)
(20)

(21)
第i(i=2,3,…,n-1)步:由(5)、(6),计算zi的导数为:
(22)
根据(12)和(22),Vi的导数为:
(23)

(24)
(25)
将(24)、(25)代入(23)可得:
(26)

(27)
(28)
由(27)和(28)代入(26)可以得到:
(29)

第n步:求得Vn的导数为:
(30)
应用Young’s不等式,由(4)可得:
(31)

(32)
(33)
由(30)、(31)、(32)和(33)可得:
(34)

3.2 稳定性分析
定理1考虑具有未知控制方向和输入死区的非线性系统(1),在假设3和引理5的条件下,基于模糊状态观测器设计的控制器(18)、(27)、(32)和自适应律(20)、(28)、(29)和(33)可以保证此闭环系统内所有信号的有界性和跟踪误差在原点处的收敛性.
证明:选择李雅普诺夫函数V=Vn,由(34)有:
(35)
应用Young’s不等式,有
(36)
(37)
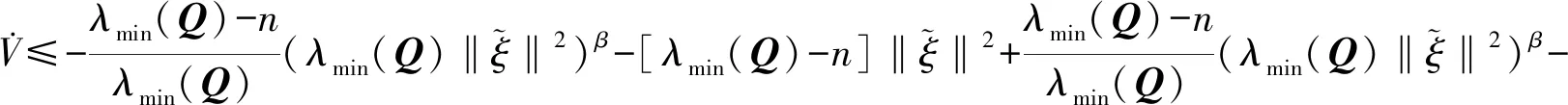
(38)
(39)
(40)
(41)
(42)
将(39)、(40)、(41)和(42)代入(38)有:
(43)
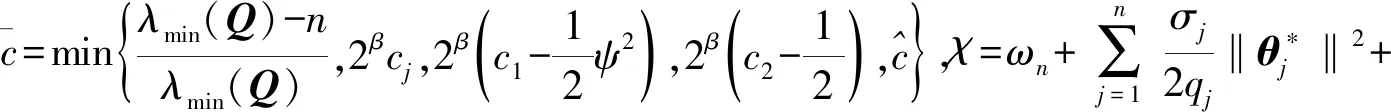

4 仿真实例
考虑下面非线性系统
(44)
式中,s1=1,s2=-1,参考信号yr=sint,对原系统进行坐标变换后新系统和模糊观测器分别为:
(45)
(46)

根据设计的控制器υ仿真结果如图1-图4所示,图1是输出信号y和参考信号yr的轨迹,图2是跟踪误差z1的仿真结果. 由图1和图2可以看出,输出信号y在控制器υ的作用下具有良好的跟踪性能. 图3 显示了经过坐标变换后式(45)的状态变量和状态估计,图4给出了模糊自适应参数.
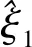

图1 输出y和参考信号yr的轨迹Fig.1 Trajectories of output y and tracking signal yr
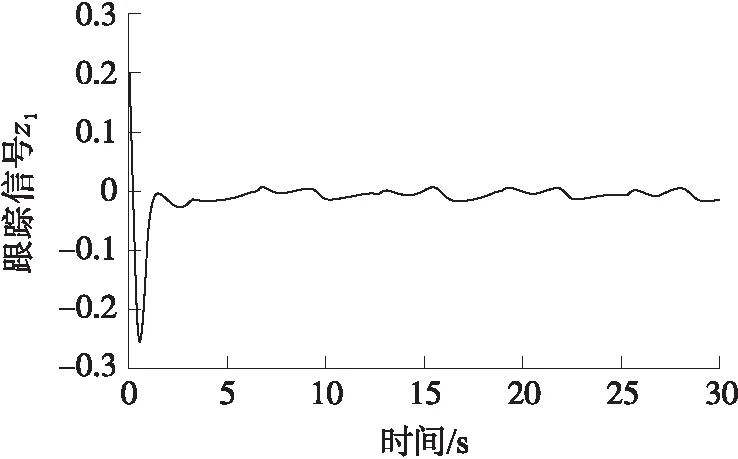
图2 跟踪误差z1Fig.2 Tracking error z1

图3 状态变量ξ1和它的估计量Fig.3 State variable ξ1 and and its estimation

图4 模糊自适应参数Fig.4 Fuzzy adaptation parameters
5 结论
本文针对一类具有输入死区以及控制方向未知且只有输出可测的非线性系统设计了半全局有限时间控制器. 首先,引入坐标变换,将所研究的系统转化为控制增益已知的等效系统. 然后,设计了一个模糊状态观测器来估计不可测的状态. 通过Nussbaum函数解决了该系统控制方向未知的困难,基于模糊状态观测器,通过反步法利用变换后的系统间接得到原系统的控制器. 此外,由仿真算例可以看出在该控制器的作用下跟踪误差在有限时间内保持有界并收敛至原点的一个小邻域内,且由引理4可知闭环系统中的所有信号都保持有界.
