基于改进遗传算法的机器人路径规划方法
2021-10-21汤云峰李鑫煌林智昌刘益剑
汤云峰,赵 静,谢 非,李鑫煌,林智昌,刘益剑
(1.南京师范大学电气与自动化工程学院,江苏 南京 210023) (2.南京邮电大学自动化学院、人工智能学院,江苏 南京 210023) (3.江苏省物联网智能机器人工程实验室,江苏 南京 210023) (4.南京中科煜宸激光技术有限公司,江苏 南京 210038)
路径规划[1-2]有着广泛的应用. 静态环境下的路径规划适用于搬运机器人、搜救机器人等领域[3],这类问题均为静态情况下面向已知环境信息,如何安全地避开障碍物找到并到达目的地的最短路径问题[4-5]. 为解决此类问题,需先进行环境建模,最常用的方法是栅格法与多种智能仿生算法[6-7](如蚁群算法[8]、遗传算法[9]、人工鱼群算法[10]等)结合使用,但均存在一定的缺陷. 国内外学者对此进行了大量研究,一直在探索新的路径规划方法或改进已有算法. 遗传算法在路径规划领域是一种有效可行的优化方法,已有多种改进遗传算法被提出. 文献[11]在适应度函数中引入倒角算子,加快了收敛速度;文献[12]采用变长编码方案,避免了遗传算子的复杂化,节约了计算成本,使收敛速度加快;文献[13]提出一种改进的交叉算子,使得算法的早熟收敛得到明显改善,并提出了一种考虑距离、安全性和能量的新的适应度函数,有助于算法找到最优路径;文献[14]提出一种新的遗传修正算子,增强了改进的遗传算法逃出局部最优路径的能力;文献[15]提出自适应遗传算法,使收敛速度加快的同时保证了机器人行驶的安全性.
基本遗传算法在机器人路径规划中存在收敛速度慢、易陷入局部最优解的问题[16]. 许多改进算法未考虑机器人的转弯次数,转弯次数过多时会消耗更多的能量,安全性也会降低. 本文提出一种改进的遗传算法,针对转弯次数较多问题,在适应度函数中考虑了长度因子和平滑度因子,并根据机器人行走时转弯角度的大小对平滑度因子加上了不同程度的惩罚,转弯角度越小惩罚越大,在进行轮盘赌选择时被选择的概率越小,有效减少了机器人转弯次数;针对收敛速度慢、易陷入局部最优解问题,在进行轮盘赌时加入精英选择策略,将每次迭代后的最优个体保留至下一代,同时让交叉、变异概率自适应改变,提高了算法逃离局部最优路径的能力,加快了算法的收敛速度.
1 基于改进遗传算法的移动机器人路径规划方法
本文在遗传算法的适应度函数中考虑了长度因子和平滑度因子,在平滑度因子中加入了惩罚操作,同时对交叉、变异概率进行了调整,并引入精英保留策略以保证个体的高适应度. 改进后的遗传算法流程图如图1所示.
1.1 环境建模
利用栅格地图表示移动机器人实际工作环境,路径上的障碍物由一定比例黑色方块替代,不足部分仍然填满栅格,白色方块为可行走空间,如图2所示.

图1 改进遗传算法的流程图Fig.1 The flow chart of improved genetic algorithm

图2 栅格地图Fig.2 Grid-based map
初始化种群的具体过程为:
步骤1 设定算法所需各项参数;
步骤2 判断栅格是否连续,判断方法为:
Δ=max{abs(xi+1-xi),abs(yi+1-yi)},
(1)
式中,(xi,yi),(xi+1,yi+1)为两个栅格对应的坐标. 当Δ=1时,表示两栅格连续,否则利用平均值法插入栅格,计算方法为:
(2)
步骤3 若P′i序号栅格附近均为障碍物栅格,则淘汰此条路径,重复上述步骤直至生成一条可行路径.
1.2 适应度函数的建立
适应度的高低决定了个体适应能力的大小,当适应度较高时易于生存,反之则会被淘汰,可用以判断个体的优劣程度[17]. 在机器人的路径规划中,长度是首要考虑因素,且机器人在行进时存在一定的转弯角度,因此本文在适应度函数中考虑了长度因子和平滑度因子,新的适应度函数如下:
Ffit=a×F1+b×F2,
(3)
式中,a、b为二者权重;F1为长度因子:
(4)
式中,LLength为路径长度.F2为平滑度因子:
(5)
(6)
式中,(xi+1,yi+1)表示机器人当前时刻所在位置;(xi,yi)表示其前一时刻所在位置;(xi+2,yi+2)表示其下一时刻所在位置;θ为机器人转弯角度. 由于运动学和动力学的约束,转弯角度不宜过大,因此当机器人转弯时给予适当的惩罚,减小其转弯的概率. 利用余弦函数判断转弯角度的大小,分别对钝角、直角、锐角给予5、30、1 000的惩罚.
1.3 遗传操作
1.3.1 选择操作
在遗传算法中使用轮盘赌法选择下一代个体,随机性会使适应度高的个体存在未被选中的可能. 为了避免此情况的发生,引入精英保留策略. 在使用轮盘赌选择前,计算所有个体适应度,把适应度最优的个体保留至下一代,不参与轮盘赌选择,剩余个体通过轮盘赌法选出较优个体,之后与精英个体进行交叉变异操作,以提升算法寻找最优解的能力,防止算法陷入局部最优解.
1.3.2 交叉和变异操作
交叉概率(crossover probability)以Pc表示. 交叉操作在路径规划中指将已搜索到的两条父代路径在相交的点(随机确定)进行交换,交换后保留较短路径,摒弃较长路径,与基因的分裂与重组类似. 在进行交叉操作后,子代路径的适应度可能高于父代路径,达到寻优的目的.
变异概率(mutation probability)以Pm表示. 变异操作在路径规划中指将已搜索到的父代路径以概率Pm进行翻转,结合交叉操作可能得到适应度更高的子代路径. 遗传算法所拥有的变异行为能使其尽可能多地搜索到可行路径,有利于其逃离局部最优解.
在基本算法中,Pc、Pm固定不变. 对于交叉操作,若Pc较大,则适应度高的个体被破坏的概率会变高;若Pc较小,则搜索的速度会变慢. 对于变异操作,若Pm较大,则随机变异个体增多,不利于搜索;若Pm较小,则存在个体不变异的可能,算法的搜索能力降低. 因此,对Pc和Pm采取自适应操作:
(7)
(8)
式中,i表示当前进化次数;Mg表示最大进化次数. 为了避免算法陷入随机搜索,对变异概率设置上限Pm_max.
2 实验结果与分析
将本文算法与基本遗传算法和文献[18]算法进行仿真对比,使用MATLAB在20×20的地图中实验. 文献[18]算法求解适应度函数时加入平滑度函数,一定程度上提高了收敛速度,但其中加入的惩罚项以长度为参考值,存在转弯角度为锐角和钝角时路线长度相同的问题,无法准确对机器人路径进行惩罚,导致转弯次数过多;未使交叉、变异概率自适应调整,在复杂障碍物环境中存在无法搜索到最短路径的问题.
本文算法的主要参数设定为:种群规模M=100;权重系数a=1,b=7;初始交叉概率Pc=0.9;初始变异概率Pm=0.01;最大进化次数Mg=100;变异概率上限Pm_max=0.3. 图3~图8为仿真结果.

图3 简单地图中基本遗传算法路径Fig.3 Basic genetic algorithm path in simple map
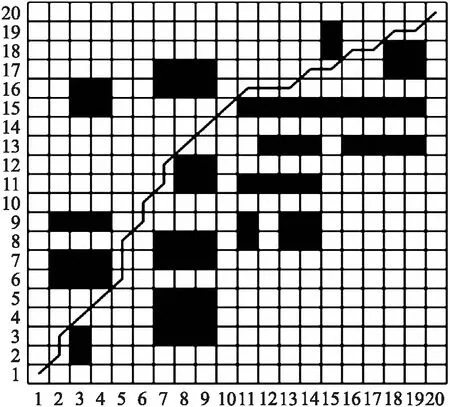
图4 简单地图中文献[18]遗传算法路径Fig.4 Genetic algorithm path of literature[18]in simple map
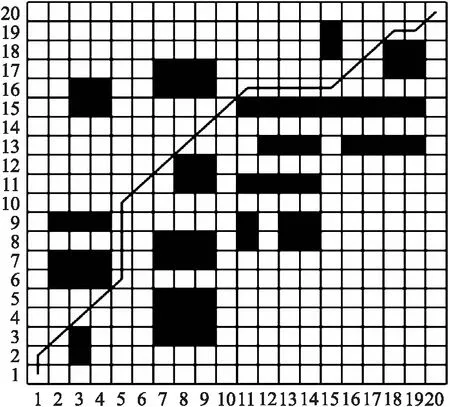
图5 简单地图中本文遗传算法路径Fig.5 Genetic algorithm path of this paper in simple map

图6 简单地图中基本遗传算法的收敛曲线Fig.6 Convergence curve of basic genetic algorithmin simple map
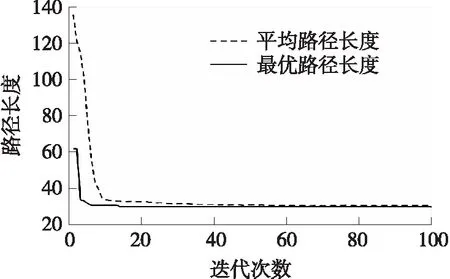
图7 简单地图中文献[18]遗传算法的收敛曲线Fig.7 Convergence curve of literature[18]in simple map

图8 简单地图中本文遗传算法的收敛曲线Fig.8 Convergence curve of this paper in simple map
由图3~图5可看出,3种算法均能找到最短路径. 在基本遗传算法和文献[18]算法中,机器人分别进行了13次和16次转弯,能耗较大且不利于机器人的行驶;本文算法中机器人仅进行了7次转弯,大大减少了转弯次数,提升了机器人的安全性,降低了能耗.
由图6~图8可看出,3种算法分别经过30次、14次、17次迭代收敛到了最短路径,文献[18]算法与本文算法收敛到最短路径时的迭代次数相近.
为了避免偶然性,对3种算法分别进行20次仿真实验进行对比,如表1所示.
本地图理论上的最优路径为29.8,基本算法有时无法找到最短路径,文献[18]算法和本文算法均能找到最短路径. 从表1中可以看出,文献[18]算法转弯次数较多,但找到最短路径的能力及平均迭代次数均优于基本算法. 本文算法中机器人转弯次数最少,且收敛速度较快,算法的优越性得到了初步证明.

表1 简单地图中3种算法仿真实验对比Table 1 Comparison of simulation experiments of three algorithms in simple map
为进一步验证本文算法的性能,在更复杂的障碍物栅格地图中进行仿真实验. 仿真结果如图9~图14所示.

图9 复杂地图中基本遗传算法路径Fig.9 Basic genetic algorithm path in complex map

图10 复杂地图中文献[18]遗传算法路径Fig.10 Genetic algorithm path of literature[18]in complex map

图11 复杂地图中本文遗传算法路径Fig.11 Genetic algorithm path of this paper in complex map

图12 复杂地图中基本遗传算法的收敛曲线Fig.12 Convergence curve of basic genetic algorithmin complex map

图13 复杂地图中文献[18]遗传算法的收敛曲线Fig.13 Convergence curve of literature[18]in complex map

图14 复杂地图中本文遗传算法的收敛曲线Fig.14 Convergence curve of this paper in complex map
从图9~图11可看出,当障碍物地图更为复杂时,基本遗传算法始终无法找到最短路径且规划出的路径杂乱无章,故在本地图中不再讨论;文献[18]算法未找到最短路径,且转弯次数较多;本文算法在复杂的地图中转弯次数依然较少.
本地图中理论上的最优路径为31.56. 由图12~图14可以看出,基本遗传算法在迭代至第60次时搜寻到的路径长度为50.38;文献[18]算法在迭代到第61次时路径长度收敛于32.97;本文算法在迭代到第38次时收敛到的最短路径长度为31.56,搜索到了最短路径.
对3种算法分别进行20次仿真实验进行对比,如表2所示.

表2 复杂地图中3种算法仿真实验对比Table 2 Comparison of simulation experiments of three algorithms in complex map
基本算法始终无法规划出一条最短路径,文献[18]算法仅规划出一次最短路径,说明以上两种算法不适用于复杂地图中的路径规划;本文算法在复杂地图中始终能够准确找到最短路径,且转弯次数较少,寻优能力得到了进一步证明.
从表1、表2可以看出,基本遗传算法由于自身的局限性,其规划效果次于改进的算法;文献[18]算法适用于障碍物较少的地图环境;本文算法在简单和复杂障碍物地图中的寻优能力、转弯次数和平均迭代次数均优于基本遗传算法和文献[18]算法,因而具有更优的路径规划能力.
3 结论
本文提出了一种改进遗传算法的机器人路径规划算法,引入带有惩罚机制的平滑度函数,减少了机器人拐弯的次数,使机器人能够更平滑地行驶至目的地;引入精英保留策略,有利于算法寻找更优解,提升算法的寻优能力;提出自适应交叉概率、变异概率,使算法的寻优能力和收敛速度都得到了提升. 实验结果表明,本文算法在简单及复杂环境下均能找到最优路径,且转弯次数较少,具有较好的路径规划能力.
