满足水功能区管理目标的中小河流纳污能力计算方法及参数取值研究

李�� 杨寅群 王艳 刘路广

摘要：由于传统中小河流水域纳污能力计算模型在模型概化、设计水文条件、水流速度、降解系数取值等方面受使用者主观影响较大，实际应用中在一定程度上制约了水环境管理目标.采用概化模型分析了传统方法的自洽性，提出了满足各类水功能区水质管理目标的中小河流纳污能力计算模型的改进方法，并在模型方法的主要参数敏感性分析及误差分析的基础上，提出了模型概化和参数取值原则，以降低主观因素对纳污能力计算结果的影响。结果表明：该方法能够保证计算结果既满足设计水文条件下的最大允许排污量，也满足水功能区水质管理目标，具有良好的通用性。

关键词：中小河流纳污能力;概化模型;误差分析;参数取值;水功能区

中图法分类号：X26文献标志码：ADOI：10.15974/j.cnki.slsdkb.2021.10.015

文章编号：1006 - 0081（2021）10 - 0081 - 07

0 引 言

“纳污能力”概念及其计算方法的提出为定量化某一水域最大污染物排放量、保护水体水质起到了重要的作用，已经成为入河污染物总量控制措施的重要依据。中国2010年颁布了《水域纳污能力计算规程》（以下简称《规程》），以其为指导全面开展了纳污能力核定工作，获得了一系列具有指导意义和应用价值的成果[1-4]。学者们在汉江、渭河、松花江、太湖流域等典型地区开展了实际研究工作[5-8]。

然而，随着纳污能力计算相关工作和研究的不断深入，发现《规程》所推荐中小河流纳污能力计算模型在模型概化、设计水文条件、水质初始条件、水质边界取值方面存在争议[3，9-11]。学者们分析了设计水文条件[12-13]、污染源和排污口概化方式及控制断面设置[14-15]、计算模型与模型参数取值[16-17]等因素对河流纳污能力计算结果的影响，并对纳污能力计算中的计算条件、参数的不确定性[18-19]进行了研究。但少有使用者定量分析《规程》中技术方法的合理性，且现有研究中所提的各种参数取值方法缺乏严谨理论分析，受主观因素影响较大，实际应用中在一定程度上制约了水環境管理目标的实现。本文从数值计算方面分析了传统方法的自洽性，提出改进的满足各类水功能区水质管理目标的中小河流纳污能力计算模型方法，并在模型方法的主要参数敏感性分析及误差分析的基础上，提出模型概化和参数取值原则，以降低主观因素对纳污能力计算结果的影响。

1 中小河流纳污能力现行计算方法分析

1.1 计算方法的自洽性分析

自洽性就是按照自身逻辑推演，自己可以证明自己至少不是矛盾或者错误的。在本文中，按照纳污能力定义，根据拟定的设计水文条件和排污情况，计算所得的纳污能力应当满足水功能区管理目标的最大允许排放量，即按照该排放强度，假设排污口断面完全混合时，水功能区内部各处均不超标，且功能区内最大浓度恰好等于功能区管理目标。但是分析表明，该方法计算出来的纳污能力并不满足上述条件，与纳污能力的定义不能完全符合，即该模型方法不满足自洽性。

《规程》中纳污能力计算依据的基本条件如图1所示。假定某水功能区起止断面分别为断面A和断面C（图1），且该功能区与其上、下游水功能区水质管理目标相同，均为[Cs]。入河排污口B废水排放强度为q，污染物最大允许排放量[Mq]，[Mq]即为待求解的该河段纳污能力。水功能区初始断面浓度[Ca=Cs]。

依据《规程》，纳污能力[Mq]计算具体过程如下。

上断面来水浓度[Ca]取值为水功能区水质管理目标：

[Ca=Cs] （1）

式中：[Ca]为上断面污染物浓度，mg/L。

在B断面与源项汇合前，污染物浓度为

[Cb1=Csexp（-kx1/u1）] （2）

与排污口B来水混合后浓度[Cb]为（因[Mq]为待求解参数，此处仅考虑排污口水量增加对上游来水的水质的影响）：

[Cb=QaQa+qCb1=QaQa+q?Cs?exp（-kx1/u1）]        （3）

式中：[Cb]为排污口混合后污染物浓度，mg/L;[Cb1]为排污口混合前污染物浓度，mg/L;[Qa]为上断面来水流量，m3/s;q为废水排放流量，m3/s;[Cs]为水质目标浓度，mg/L;K为污染物综合衰减系数，1/s;[x1]为上断面至排污口河段长度，m;[u1]为[x1]河段的平均流速，m/s。

到达末断面C时浓度为

[Cc=QaQa+qCb1?exp-kx2u2]                  （4）

式中：[Cc]为下断面污染物浓度，mg/L;[x2]为排污口至下断面河段长度，m;[u2]为[x]2河段的平均流速，m/s。

纳污能力[Mq]为

[Mq=Qa+q?Cs-Cc]                    （5）

式中：[Mq]为纳污能力，mg/s。

将上述计算所得到的纳污能力回代至排污口，假设排污口完全混合，根据质量守恒方程得排污口断面完全混合浓度[C′b]为

[C′b=Cb1?Qa+MqQa+q]                              （6）

将式（4）～（5）计算结果代入式（6）中，即排污口以纳污能力负荷排污，排污口断面完全混合浓度为

[C′b=Cs+QaQa+qCsexp-Kx1u11-exp-Kx2u2]     （7）

水功能區末断面浓度[C′c]为

[C′c=]

[Csexp-Kx2u2+QaQa+qexp-Kx1u1-QaQa+qexp-Kx1u1exp-Kx2u2]

（8）

由式（7），（8）可以看出，[C′b≥Cs]，[C′c≤Cs]，即，依据《规程》计算结果进行排污控制时，通常情况下排污口混合断面处水域水质不满足水功能区水质目标，末断面水质浓度优于水功能区水质目标，因此该控制目标并非“最大允许排放量”。在排污口至末断面之间河段会出现水质超标，仅在排污口位于功能区末断面（[x2=0）]时，能够保证排污口断面达标。

由上述分析可见，按照《规程》推荐方法在理论上不能保证水功能区的水质完全满足水功能区水质管理目标，也不能充分利用水功能区的自净能力，理论上不满足自洽性。

1.2 水功能区超标分析

由式（8）可知，对于排污控制区和缓冲区以外的其他水功能区，在排污口完全混合后断面污染物浓度超出水功能区水质目标。现就其超标幅度和超标距离进行分析。

1.2.1 超标程度

为使问题易于讨论，假设该河流为恒定流、排污口位于河段中部、上下游平均流速相等，此时[x1=x2]，[u1=u2]。

令：[β=exp（-Kx1/u1）=exp（-Kx2/u2）] ，则式（5）可写成：

[C′b=Cs+CsQaQa+qβ1-β]              （9）

其中，[QaQa+q∈0，1] ，[β1-β∈0，0.25]，即，在入河排污口混合后，断面水质超出功能区水质标准，超标倍数为[QaQa+qβ1-β]，最大超标倍数可达0.25。

1.2.2 超标距离

由上述分析可知，污水在排污口断面与上游来水混合后，会在下游形成一定距离的超标污染带。假设该超标污染带长度为x，则排污口下游x处断面水质达标为

[Cs=Cx=C′bexp-KxU]                      （10）

得到排污口下游超标距离x为

[x=UKln1+QaQa+qβ1-β]               （11）

式中：[β1-β]最大为0.25，[QaQa+q]最大为1，则超标距离x最大为

[x=UKln1.25=0.223UK]                   （12）

由式（12）可知，超标距离x取值大小取决于河段平均流速U和污染物降解系数K，即排污口下游超标距离不受人为控制。例如，当流速U=0.1 m/s，污染物降解系数 K=0.2/d时，超标距离x最大可达9.5 km。虽然水功能区末断面作为控制断面不超标，但水功能区内部可能存在部分河段超标，且超标距离不可知。对同一个排污口，不同污因子因降解系数通常不同，形成的超标距离也不同。

可见，基于现行方法计算得到纳污能力进行污染物总量控制，能保证功能区末断面达标，但无法保证整个功能区内部水质达标。这种情况，与河流水环境管理和保护的初衷不符，这也是部分水功能区所在考核断面达标，但存在黑臭水体的怪状根源。

综上所述，基于推荐方法的计算成果与纳污能力定义不一致，不满足自洽性原则;以其作为水功能区总量控制指标时，能保证水功能区末断面达标，但功能区内部存在超标河段，超标程度和超标距离均不确定。推荐方法只适用于末断面达标控制的排污控制区和缓冲区;用于其他水功能区时，排污口至达标控制断面间的水域都不能满足水功能区水质管理目标，水体的使用功能将受损。

2 修正的纳污能力计算模型

假定入河排污口污染负荷为 M g/s，根据管理要求在排污口下游距离 [X达]处达到水质目标[Cs]，与排污口污水混合前，河流中污染物背景浓度为[Cb1]，则在排污口处完全混合后浓度为

[C混=Cb1Qa+MQa+q]                           （13）

下游[X达]处浓度为

[Cs=Cb1Qa+MQa+q?exp-KX达U]                   （14）

该河段纳污能力为

[M=Qa+qCs expKX达U-Cb1Qa]      （15）

对于排污控制区或缓冲区，要求在水功能区交接断面达到下断面水质目标，因此[X达]即为排污口到水功能区交接断面的距离。对于其他水功能区，一般应要求排污口混合处达标， 即[X达] = 0 ，此时：

[M=QaCs-Cb1+qCs]                    （16）

将计算所得纳污能力再次代入式（13）计算排污口断面混合浓度，并根据式（14）计算得到水功能区水质目标管理断面浓度，等于Cs，可见该修正方法在理论上能够满足各类水功能区达标要求。因此，修正的纳污能力计算式（15）即适用于要求交接断面水质达标的排污控制区和缓冲区，也适用于对整个水功能区水质有要求的其他各类水功能区，具有更好的通用性。

3 参数敏感性分析

3.1 误差分析

基于本文提出的改进的纳污能力计算模式，分析式（15）中各参数取值对纳污能力计算结果的影响。式中，[Qa]，q，x为管理参数根据河流水功能区实际取值。对于另外两个关键参数K和U，通常因资料不足取值准确性较差，分析其取值对计算结果准确性的影响。

假定在给定河段水流速度U准确值为[Uc]，实际计算中取值[U=Uc+ΔU];降解系数K准确值为[Kc]，工作中实际取值[K=Kc+ΔK]。纳污能力计算误差形式分别为

（1）降解系数取值带来的误差计算如下：

[ΔM=Qa+qCsexpKc+ΔKxU-expKcxU]

[=Qa+qCsexpKcxUcexpKcxUcΔKKc-1]

（17）

假设所研究的污染物为外源性污染，即[Cb1=0]，令：[Qa+qCsexpKcxUc= Mk]，则相对误差为

[ΔMMk=expKcxUcΔKKc-1]                     （18）

令[EE=expKcxUc]，则相对误差为

[ΔMMk=EEΔKKc-1]                         （19）

（2）水流速度取值带来的相对误差计算如下：

[ΔM=Qa+qCsexpKcxUc+ΔU-expKcxUc]

[=Qa+qCsexpKcxUcexpKcxUc-ΔUUc+ΔU-1] （20）

同上，令[Qa+qCsexpKcxUc=Mk]，则相对误差为

[ΔMMk=expKcxUc-ΔUUc+ΔU-1]               （21）

同上，令[EE=expKcxUc]，相对误差为

[ΔMMk=EE-ΔUUc+ΔU-1]                    （22）

由式（19），（22）可知，EE对纳污能力计算结果影响较大，当其取值接近1时，相对误差受K影响降低。根据实际工作中x，[Kc]，[Uc]的取值范围，分析EE相应的取值变化区间，其结果如图2所示，其中[x∈0，10000、K∈0，0.5、U∈0，0.5]，EE的取值范围大部分位于[0，10]区间内。由图2可见，当K>0.3/d、U<0.1 m/s或x>4 000 m时，EE的值迅速变大;当流速取值较小时（如U<0.1），K，x的取值误差对于EE值影响更为显著。

3.2U的取值误差分析

EE取值范围为[0，5]、U取值与实际偏差在[-50%， 50%]区间时，纳污能力计算结果相对误差的分布如图3所示。

可见EE取值在0.8～1.4范围内时，速度U的取值误差造成的纳污能力计算结果误差较小，在EE<0.8时，U的取值无误差偏大或偏小都将导致纳污能力计算结果的相对误差显著增大，在EE>1时，U取值误差为正（偏大）时比误差为负值（偏小）时造成的误差小。

3.3降解系数K取值误差分析

EE取值范围为[0，5]、降解系数K取值与实际偏差在[-50%， 50%]时，纳污能力计算结果相对误差的分布如图4所示，可见EE取值在1附近时，降解系数K的取值误差造成的纳污能力计算结果误差较小，在EE>1时，K取值误差为负（偏小）时比误差为正值（偏大）时造成的误差小。

参数取值误差分析了计算方法的主要影响参数及其取值准确性导致的误差，提出了模型概化和参数取值原则。纳污能力计算结果受EE影响较大，在实际工作中，在河流的流速U、污染物降解系数K取值无精准结果时，为了减少参数取值引起的偏差，应当合理确定K，U，x的取值，使误差分析中的EE接近1。采用末断面达标控制时，排污口与达标控制断面的长度不宜超过4 km，当水质模型中K>0.3/d、U<0.1 m/s或x > 4 000 m时，应注意核实数值误差的影响。

4 案例分析

以府澴河为例，府澴河是长江中游北岸一级支流，发源于大洪山北麓，自北向南流经湖北省的随县、曾都区、广水、安陆、应城、云梦、孝昌、孝南、东西湖区、黄陂区等县（市、区），在武汉市湛家矶注人长江，全长348 km，是湖北省内仅次于汉江、清江的第三大水系。选取其上游随州段涢水曾都开发利用区内部涢水曾都排污控制区和涢水曾都过渡区作为研究对象，如图5所示。

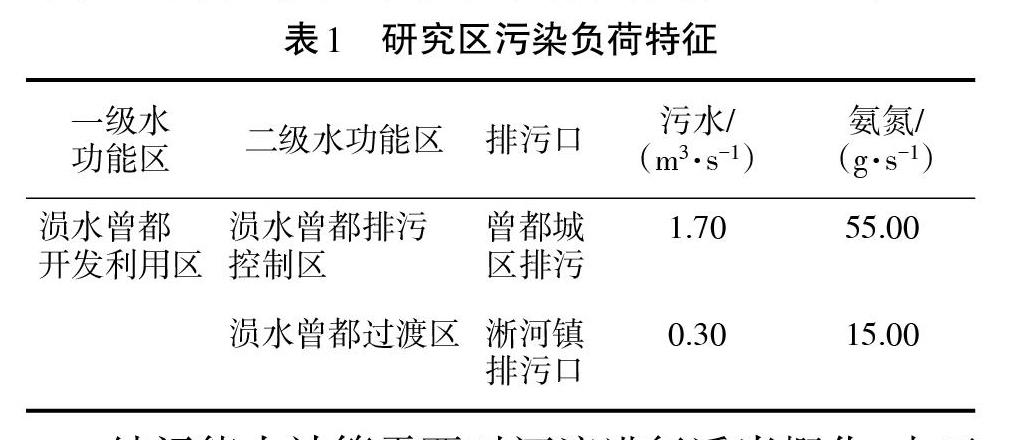
随州站多年平均流量30.5 m3/s，斷面近10 a最枯月平均流量约为6 m3/s，枯水期多次实测流速0.08～0.13 m/s。经统计，2014年研究区域废水和污染物排放强度如表1所示。

根据2014年非汛期6个月份常规水质监测结果，白云湖站氨氮平均浓度1.6 mg/L，淅河站氨氮平均浓度10.78 mg/L，该水功能区氨氮超标严重，研究该河段氨氮的纳污能力。

研究河段流速U取0.1 m/s，氨氮降解系数K参考国内类似研究成果取0.2/d，根据估算污染负荷、设计水文条件和实测水质检验各参数合理性良好。

纳污能力计算需要对河流进行适当概化，由于排污控制区长度较短（2 km），且排污集中，假设排污口位于排污控制区中部（1 km处），废水排放强度2 m3/s，研究河段涢水曾都排污控制区来水由其上游水功能区水质目标确定（Ⅲ类，氨氮1 mg/L）， 涢水曾都排污控制区无水质目标要求，下游涢水曾都过渡区末断面须达到下一水功能区水质目标（Ⅲ类，氨氮1 mg/L）管理。计算设计条件下水功能区氨氮纳污能力，并假设过渡区长度变化时《规程》方法和本文修正方法水功能区纳污能力。水功能区纳污能力计算结果见表2。

由表2可见，在现状水功能区划条件和两种假设情形下，《规程》推荐模型计算的纳污能力值均小于本文修正方法计算得到的值。当排污口排放强度分别为规程方法和修正方法计算所得的纳污能力时，计算排污口断面完全混合浓度和水功能区末断面浓度，结果表明：规程方法排污口断面浓度均小于修正方法、末断面浓度均小于下游水功能区水质管理目标，而按照本文修正方法计算所得纳污能力排放时，末断面浓度恰好等于下游水功能区水质管理目标。因此，本研究提出的改进模型在保证水功能区水质满足管理目标的同时能够更充分利用水功能区纳污能力。

5 结论与建议

（1）《规程》中河流纳污能力计算方法存在不满足自洽性、应用中受主观因素影响较大的问题。据其计算得到的水域纳污能力用于按照末断面达标控制管理的排污控制区和缓冲区时，未充分利用水域的自净容量，而用于其他对水功能区内水体有管理目标要求的各类水功能区时只能保证功能区末断面达标，水功能区内部存在水质超标河段，不符合《水法》和《水功能区划分标准》对于水功能区水质管理的要求，不利于水资源的管理和保护。

（2）研究提出了改进的满足各类水功能区水质管理目标的中小河流纳污能力计算模型方法，该方法理论满足自洽性，既适用于要求交接断面水质达标的排污控制区和缓冲区，也适用于对整个水功能区水质有要求的其他各类水功能区，具有良好的通用性。

（3）分析了计算方法的主要影响参数及其取值准确性导致的误差，提出了模型概化和参数取值原则。在实际工作中，在河流的流速U、污染物降解系数K值取值无精准结果时，U取值偏大、K取值偏小时纳污能力计算结果的相对误差较小。

（4）根据水功能区监督管理办法对于水功能区水质管理的要求，对于排污控制区和缓冲区，以缓冲区与下一水功能区交接断面达标控制，采用末断面达标模型;对于其他各类水功能区，应采用首断面达标模型，以保证各水功能区达到其水质管理目标。

（5）对于排污控制区以外的水功能区，当按照排污口断面达标管理不能满足排污需求时，可考虑将排污河段改设为排污控制区和缓冲区，以实现经济社会发展对排污的客观需求与水功能区管理法规的统一。

参考文献：

[1] 闫峰陵，刘扬扬，樊皓，等. 基于水功能区纳污能力的攀枝花限制排污总量研究[J]. 长江流域资源与环境，2016，25（11）： 1774-1780.

[2] 周孝德，郭瑾珑，程文. 水环境容量计算方法研究[J]. 西安理工大学学报，1999，15（3）：3-8.

[3] 路雨，苏保林. 河流纳污能力计算方法比较[J]. 水资源保护，2011（4）：5-9.

[4] 喬维川，谢慧芳，陈建国. 太湖流域丹阳市水体纳污能力分析及总量控制规划[J]. 环境科学与管理，2010，35（4）： 47-50.

[5] 张宏斌，赵洁，訾香梅. 渭河干流纳污能力与限制排污总量计算分析[J]. 陕西水利，2010（1）： 35-38.

[6] 潘建波，张修宇. 水体纳污能力计算模型在松花江流域的应用[J]. 人民黄河，2011，33（6）：61-63，66.

[7] 李红军，刘锐，张建元，等. 资料缺乏地区水功能区纳污能力计算——以都匀市清水江为例[J].  节水灌溉， 2015（5）：49-51.

[8] 陈君，张万顺，方芳. 南水北调工程对汉江中下游有效环境容量的影响研究[J]. 环境科学与技术，2009，32（11）：135-139.

[9] 黄茁，冯雪，赵鑫，等. 基于数值模拟的纳污能力计算方法探讨[J]. 长江科学院院报，2015，32（6）： 15-19.

[10] 赵鑫，黄茁，李青云. 我国现行水域纳污能力计算方法的思考[J]. 中国水利，2012（1）： 29-32.

[11] 侍猛，马勇骥，崔勇. 河流纳污能力计算方案及主要影响分析[J]. 江苏水利，2017，（4）：46-49.

[12] 张晓，罗军刚，解建仓.  考虑取水口和支流的河流纳污能力计算模型研究与应用[J]. 水利学报，2017，48（3）：317-32.

[13] 肖洋，喻婷，潘国艳，小型城市湖泊纳污能力核算中设计水文条件研究[J]. 人民长江，2019，50（11）：80-83，90.

[14] 程声通.  河流环境容量与允许排放量[J].  水资源保护，2003（2）： 8-10，61.

[15] 张海鸥，闵涛，罗军刚. 基于多模型的渭河陕西段纳污能力研究[J]. 水资源与水工程学报，2012，23（ 6） ： 89-93.

[16] 赵蜀汉，徐汉光.  曼宁公式应用于水体纳污能力设计参数计算的探讨[J].  水利水电快报，2002，23（19）： 24-26.

[17] 罗慧萍，逄勇，徐心彤.  江苏省太湖流域水功能区纳污能力及限制排污总量研究[J].  环境工程学报，2015，9（4）：1559-1564.

[18] 彭振华，尤爱菊，徐海波.  河流纳污能力计算一维模型主要参数的取值分析[J].  浙江水利科技，2016，44（6）：46-49.

[19] 劳国民.  纳污能力计算一维模型中各参数的敏感性分析[J]. 浙江水利科技，2003（2）：18-19.

（编辑：李 晗）

Research of water environment pollution bearing capacity calculation method for small and medium rivers and parameters analysis

LI Yan1，2， YANG Yinqun3 ， WANG Yan4， LIU Luguang1，5

（1. Hubei Water Resources Research Institute， Wuhan 430070， China;  2. Hubei Jinlang Survey and Design Co.， Ltd， Wuhan 430070， China;  3. Changjiang Water Resources Protection Institute， Wuhan 430051，China;  4. School of Resources and Environmental Sciences， Wuhan University， Wuhan 430079，China;   5.Hubei Water Saving Research Center ，Wuhan  430070， China）

Abstract： Because the traditional calculation model of the pollution bearing capacity of small and medium rivers has problems of subjective affection of users in model generalization， design hydrological conditions， flow speed， degradation coefficient value， etc. ， which gives a restriction to water environment management goals to a certain extent in practical application. The generalized model is employed to analyze the self-consistency of the traditional method， and an improved method for the calculation model of small and medium-sized rivers is proposed to meet the water quality management objectives of various water function zones， and on the basis of sensitivity analysis and error analysis of the main parameters of the model method， the principles of model generalization and parameter selection are proposed to reduce the influence of subjective factors on the calculation results of pollution bearing capacity. The results show that this method can ensure that not only the calculation result is the maximum allowable sewage discharge under the designed hydrological conditions， but also meets the water quality management objectives of the water function zone， and has good versatility.

Keywords： water environment pollution bearing capacity of small and medium rivers ; Generalized model;error analysis; parameter values;  water function area