山西省浊漳河北源流域洪水峰量演变规律及联合分布研究

宋佳佳 张芳齐

摘要：为研究山西省浊漳河北源流域洪水特征，采用浊漳河北源石栈道水文站1957～2016年共60 a逐日流量资料，对洪峰流量、1日洪量进行研究。通过Mann-Kendall非参数检验法，揭示了该水文站洪峰流量和1日洪量演变特征及规律，并通过Copula函数研究了浊漳河北源流域洪水峰量联合分布情况。结果表明：洪峰流量和1日洪量均呈现明显的下降趋势;时间序列上洪峰流量在1971年后有显著的下降趋势，1日洪量在1974年后呈现显著的下降趋势;Copula函数可较好拟合浊漳河北源洪水峰量的相关关系。研究成果可为该流域水利工程规划设计和风险评估提供科学依据。

关键词：洪峰流量;1日洪量;Mann-Kendall;Copula函数;浊漳河北源流域

中图法分类号：TV122.5 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2021.10.001

文章编号：1006 - 0081（2021）10 - 0006 - 06

0 引 言

在全球气候变化和人类活动的影响下，流域内洪水情势发生变化，需对其变化和发展趋势进行分析。洪水峰量是研究洪水的重要特征，它不仅反映洪水的强度，也预示防洪的级别，因此对洪水峰量的演变规律研究尤为重要[1]。洪水需要多个特征变量才能完整描述，如洪峰、峰现时间、时段洪量和洪水历时等存在相关性的特征变量。多个特征变量的联合分析相比于单变量分析能更好地描述洪水特性并将有利于建设安全的防洪工程系统。Copula函数是多变量联合分布构建理论与方法的重大突破，De Michele[2]采用Copula函数建立了降雨强度和降雨历时的联合概率分布。熊立华等[3]采用Copula函数构建了长江流域某站点洪峰和洪量的联合分布。近十几年来，利用Copula函数研究洪水的成果众多，主要集中在洪水峰量、洪水历时等变量的联合分布和重现期研究上[4]。多变量重现期以联合重现期、同现重现期和Kendall重现期应用最为广泛[5] ， 结构荷载重现期[6]也引起了关注。

为较全面研究浊漳河北源流域洪水极端事件，需研究多变量的联合分布，Copula函数是实现这种相关性分析的有效方法。本文以浊漳河北源流域为例，采用石栈道水文站实测水文资料，利用Mann-Kendall非参数检验法，揭示了浊漳河北源洪水峰量的演变特征及规律。洪水峰量均单独服从P-Ⅲ型分布，通过Copula函数将浊漳北源流域洪水峰量结合起来建立联合分布模型，为水利工程规划设计和风险评估提供科学依据。

1 研究区概况

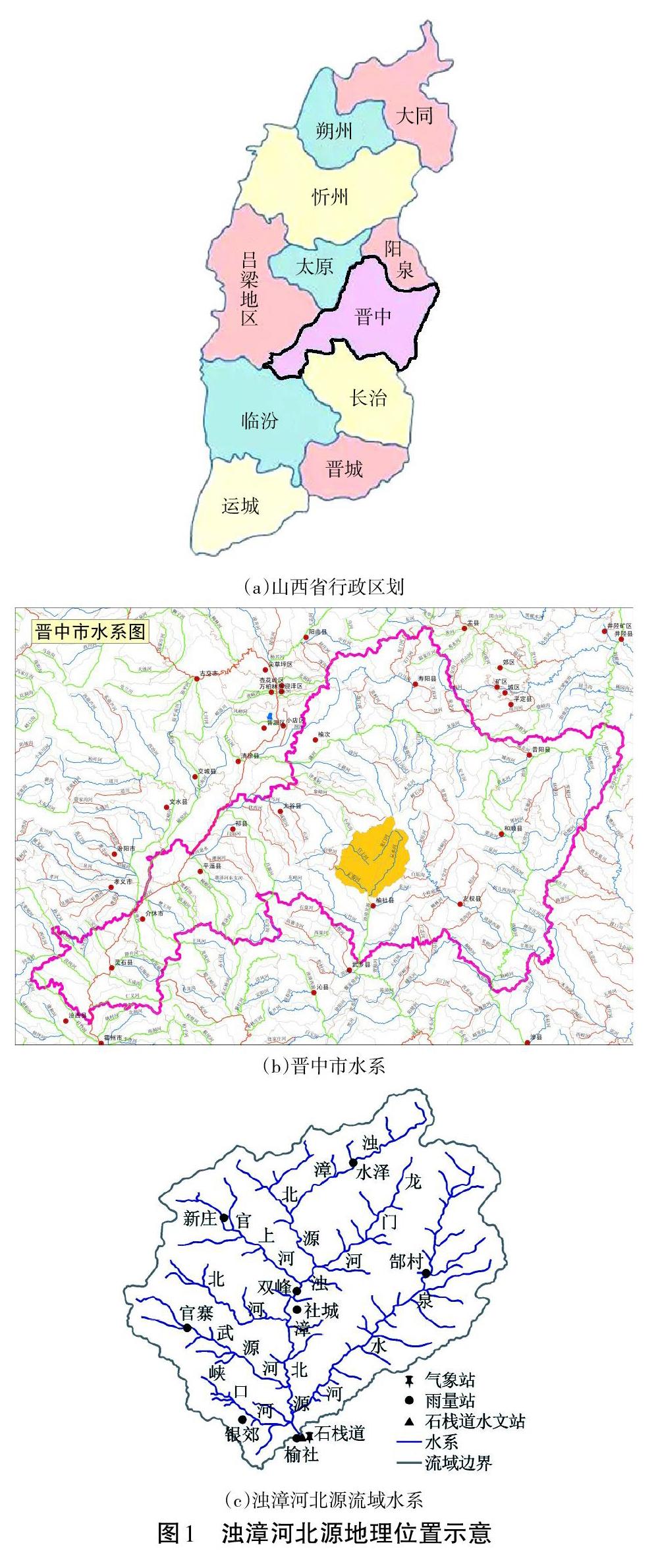
浊漳河属漳卫南运河水系，上游有北、南、西三大支流，称浊漳北源、浊漳南源、浊漳西源。浊漳河北源是浊漳河三源之一，发源于山西省晋中市榆社县社城镇焦红寺大牛村，在山西省长治市襄垣县小峧村南汇入浊漳河干流（图1）。浊漳北源流域总面积3 797 km2，主河道长135 km。

2 数据与方法

2.1 数据来源

本文数据来源为浊漳河北源河道榆社县石栈道水文站，利用石栈道水文站1957～2016年共60 a逐日流量资料，采取年内日最大选样法选取洪峰流量、1 日洪量为研究对象，运用Mann-Kendall检验法对洪水峰量进行演变规律分析，并采用Copula函数对石栈道水文站站址处洪水峰量的联合分布进行研究。

2.2 数据资料“三性分析”

2.2.1 可靠性

石栈道水文站位于晋中市榆社县石栈道村浊漳河北源河道上，地理坐标为东经112°58′、北纬37°04′，于1957年6月设立。该站属于山西省水文水资源勘测局，为基本水文站。该站观测编制水文资料均符合有关规程、规范要求，资料质量可靠，精度满足水文分析要求。

2.2.2 一致性

石栈道水文站上游约15 km处建有双峰水库，控制流域面积190.2 km2。双峰水库自1975年兴建以来，共经过两次续建，于2008年完成全部工程，达到现状规模。由于库区移民问题，2017年才开始蓄水。本文选取石栈道水文站1957～2016年实测流量系列资料具有一致性。

2.2.3 代表性

石栈道水文站实测流量系列资料为1957～2016年，流量系列相对较长，包括了丰、平、枯年。绘制石栈道水文站模比差积曲线及洪峰流量和1 日洪量变化过程线（图2～3）。石栈道水文站年最大洪峰流量和1日洪量变化规律基本一致，即大洪峰大洪量，小洪峰小洪量，但年最大洪峰流量和最大1日洪量不一定出现在同一日。石栈道水文站实测流量系列资料具有代表性。

2.3 研究方法

2.3.1 Mann-Kendall非參数检验法

本文采用Mann-Kendall非参数检验法研究水资源演变特征[7]，选择95%的置信水平检验，取值为1.96。同时，利用Mann-Kendall非参数检验法进行突变识别。

2.3.2 边缘分布函数

P-Ⅲ型曲线是一条一端有限一端无限的不对称单峰、正偏曲线，被引入水文统计中后，中国基本采用P-Ⅲ型曲线，其概率密度函数见式（1）。本文选用矩法估计，得出P-Ⅲ型曲线的参数[5]，假设一随机变量[X（x1，x2，...，xn）]：

[f（x）=βαΓ（α）（x-a0）α-1e-β（x-a0）] （1）

其中，                    [α=4C2s]

[β=2xCvCs]

[a0=x1-2CvCs]

[x=1ni=1nxi]

[Cv=i=1nki-12n-1]

[Cs=i=1nki-13（n-3）C3v]

[ki=xix（i=1， 2， ...， n）]

式中：[α]，[β]，[a0]分别为P-Ⅲ型分布的形状、尺度和位置参数;[Γ（α）]为伽玛函数;[x]，[Cv]，[Cs]分别为系列均值、变差系数、偏态系数。

2.3.3 Copula函数与参数估计

通过洪水峰量来分析洪水频率及重现期时，需计算洪水峰量两者的联合关系，水文领域中常利用Copula函数建立两者的联合分布[7-8]。常用的Copula函数分为Archimedean、椭圆型和二次型三大类[9] 。 其中，Archimedean Copula函数具有结构简便、计算相对简单、可构造形式多样、适应性强等优点，在实际应用中较为广泛。分析洪水事件中最常用的Archimedean Copula 函数主要有Gumbel-Hougaard、Clayton和Frank Copula。

本文先计算出3种Copula函数的参数θ，然后采用Kolmogorov-Smirnov检验的统计值对Copula函数模型进行检验，选用均方根误差（RMSE）确定拟合优度最高的Copula函数。利用选取的最优Copula函数分析洪水峰量的联合重现期和同现重现期，可以更好地掌握洪水事件特征，并应用于设计洪水估算和风险分析。

假设二维随机变量D和S，它们的边缘分布函数是[u=FD（d）=P（D≤d）]，[v=FS（s）=P（S≤s）]，聯合分布函数为[FD，S（d， s）=P[D≤d， S≤s]]，则三者表示为

[u=FD（d）， v=FS（s）]，

[FD， S（d， s）=exp{-[（-lnu）θ+（-lnv）θ]1θ}]

[FD，S（d， s）=（u-θ+v-θ-1）-1θ]

[FD， S（d， s）=-1θln[1+（e-θu-1）（e-θv-1）（e-θ-1）]]

式中：θ为Copula函数的参数。

本研究采用相关指标法进行Copula函数参数估计，结果如表1所示。

二维Copula函数经验频率计算公式如下：

[Po（i）=（mi-0.44）/（n+0.12）] （2）

式中：[mi]为联合观测样本中满足条件[D≤di]且[S≤si]的观测个数，[n]为样本容量

采用均方根误差评定各种Copula函数拟合结果

[RRMSE=1ni=1nPc（i）-Po（i）2] （3）

式中：[Pc（i）]为理论联合频率值，[Po（i）]为经验联合频率值。

[TDS=E（L）PD>d?S>s = E（L）1-FD（d）-FS（s）+FD， S（d，s）] （4）

[TDS′=E（L）PD>d?S>s=E（L）1-FD， S（d， s）]（5）

式中：[TDS]为洪旱事件的同现重现期（[D>d]且[S>s]），[TDS′]为洪旱事件的联合重现期（[D>d]或[S>s]），[E（L）]为洪旱间隔的期望值。

根据重现期来描述洪水事件的严重性，洪水峰量联合分布的重现期包括[D>d]或[S>s]和[D>d]且[S>s]两种情况。

3 洪水峰量突变及显著性水平检验

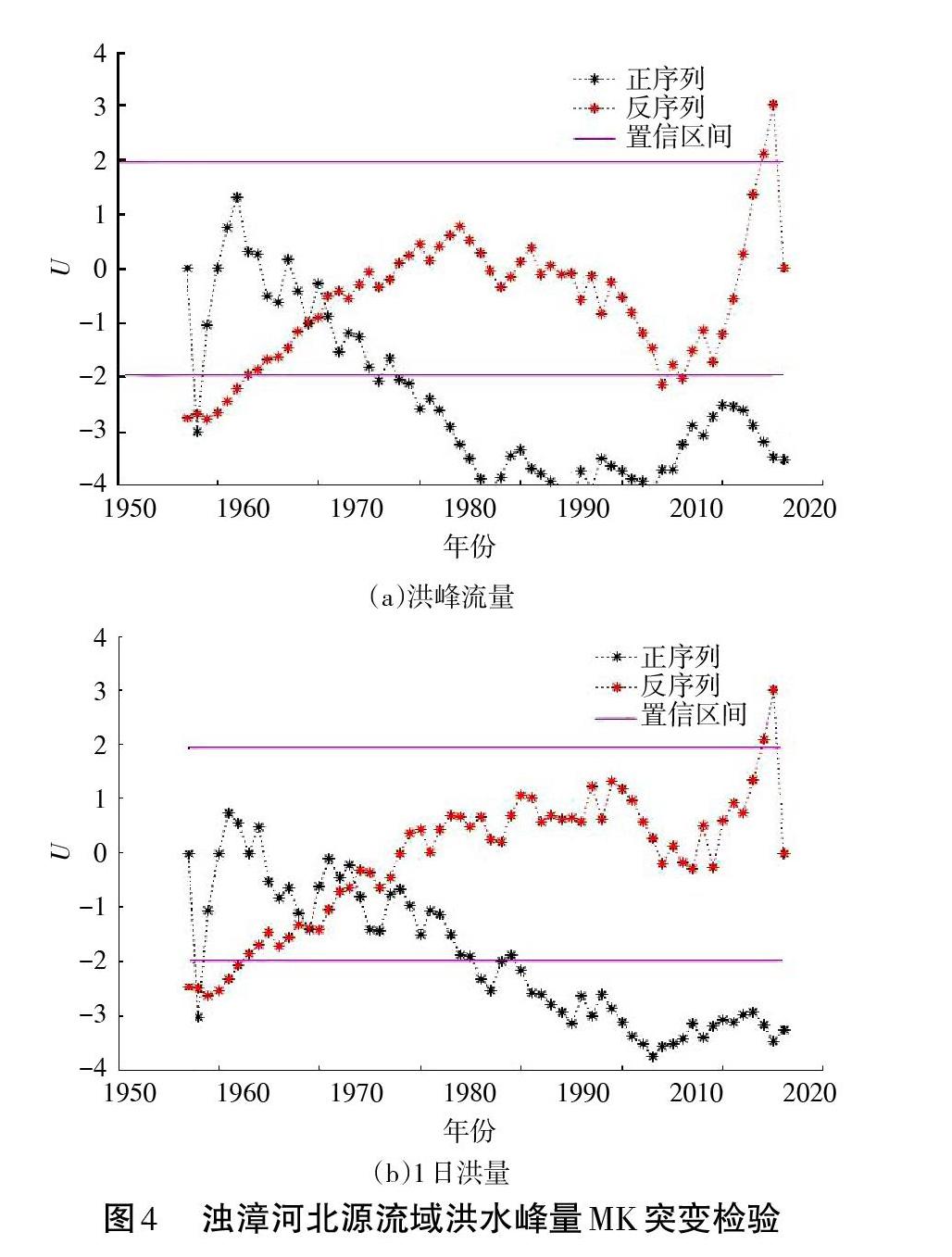
根据M-K检验成果（图4），洪峰流量在1960～1964年处于增长波动变化，其他年份均呈现波动减少变化。洪峰流量UF和UB曲线相交于1971年，且均落于0.05显著性水平阈值内，即洪峰流量在1971年出现突变，因正序列曲线在1976年突破0.05显著性水平阈值，表明洪峰流量出现显著性突变减少。

1日洪量在1960～1964年处于增长波动变化，其他年份均呈现波动减少变化。1日洪量UF和UB曲线相交于1974年，且均落于0.05显著性水平阈值内，即1日洪量在1974年出现突变，因正序列曲线在1985年突破0.05显著性水平阈值，表明1日洪量出现显著性突变减少。石栈道水文站1957～2016年洪水峰量平均值及UF均值见表2。

4 洪水峰量联合分布研究

4.1 洪水特征变量边缘分布

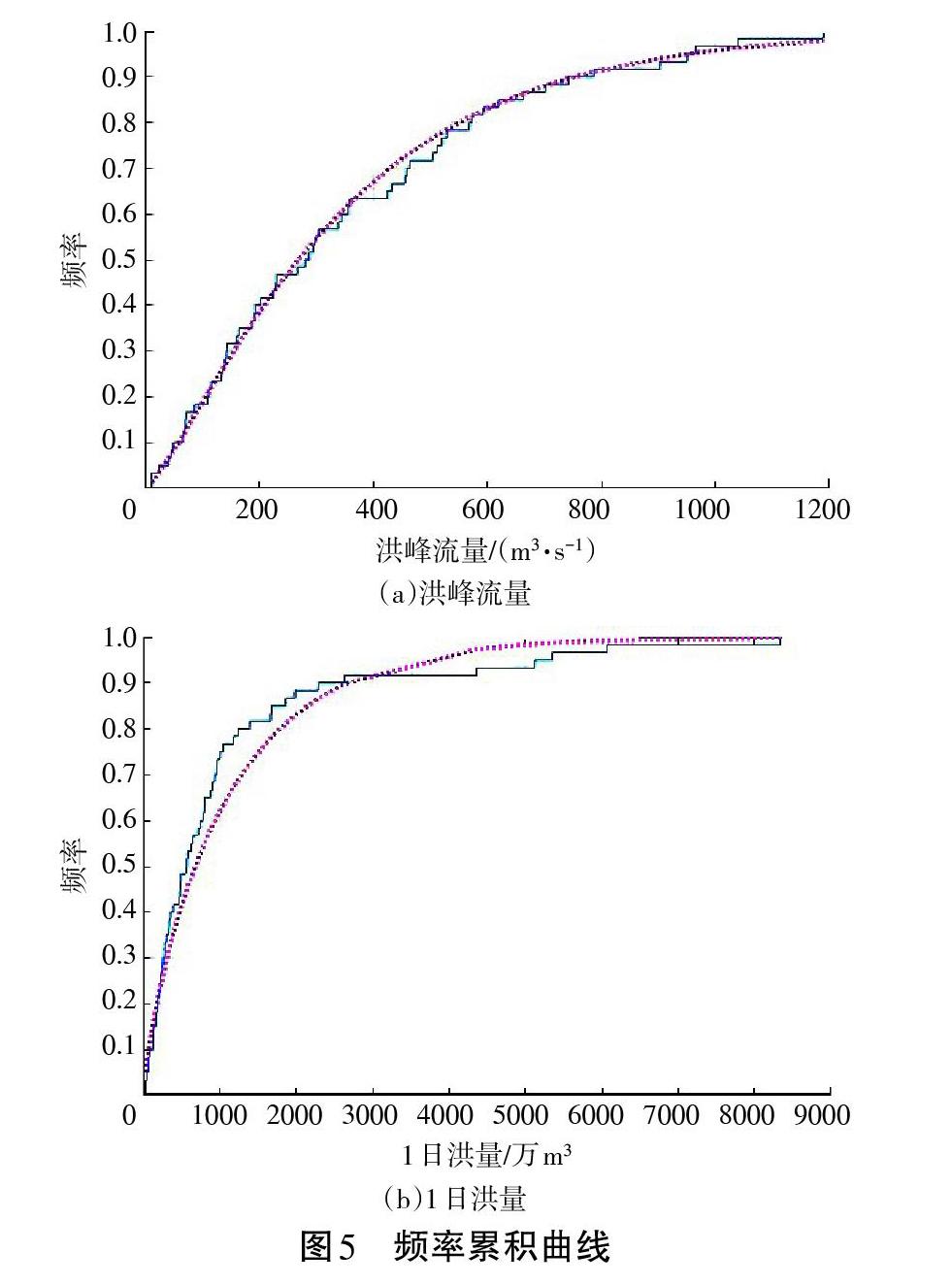
采用适线法得到石栈道水文站洪水峰量的频率曲线。洪峰流量采用[Q均值=353.78] m3/s，[Cv=0.84]，[Cs/Cv=1.82];最大1日洪量采用[W均值=536.10]万m3，[Cv=0.94]，[Cs/Cv=2.16]。同时，采用Kolmogorov-Smirnov进行检验，洪峰流量和1日洪量K-S统计检验值分别为0.063 3和0.133 5，显著水平0.05对应的临界值是0.172 3，检验结果均为0，通过检验，可认为洪峰流量和1日洪量均服从P-Ⅲ型分布。绘制洪峰流量和1日洪量的频率累积曲线，见图5。

4.2 Copula函数参数估计及拟合优度检验

采用Gumbel-Hougaard、Clayton和Frank Copula三种Copula函数建立洪水峰量的联合分布，分别运用相关指标法估计Copula函数参数，并采用均方根误差评定各种Copula函数拟合结果。结果表明：浊漳河北源石栈道水文站适合运用Gumbel-Hougaard Copula进行洪水峰量特征分析，拟合误差仅为0.300 5（表3）。

4.3 组合变量分布函数与单变量分布函数对比

（1）组合变量与单变量对应的重现期不同。1996年最大洪峰流量为951 m3/s，最大1日洪量为1 866万m3，由P-Ⅲ曲线可知，洪峰流量为951 m3/s时，重现期为15 a，洪量为1 866万m3时重现期为20 a。按G-H Copula函数洪水峰量联合分布计算，同时发生最大洪峰流量为951 m3/s、最大1日洪量为1 866亿m3大洪水的重现期为59 a。采用边缘分布函数时，1996年场次洪水洪峰流量的重现期为15 a，洪量的重现期为20 a。采用G-H Copula联合分布函数时，相同大小的洪峰或洪量任一出现的联合重现期[TDS′]为13 a，相同大小的洪峰和洪量同时出现的同现重现期[TDS]为59 a。

（2）联合重现期和同现重现期可作为实际重现期的区间估计。选取不同的边缘分布重现期得到联合分布重现期，边缘分布的重现期介于[TDS′]与[TDS]之间， 联合分布的两种重现期可以看作边缘分布的两种极端情况。可以根据联合分布的重现期作为實际重现期的区间估计，当边缘分布的重现期T为2 a时，石栈道水文站实际重现期为1.3～2.7 a，当边缘分布的重现期为100 a时，石栈道站实际的重现期在74.6～142.3 a之间，见表4。

5 结 论

（1）根据洪水峰量的趋势性分析，洪峰流量和1日洪量均呈现显著的下降趋势，洪峰流量在1976年以后开始表现出明显的下降，1日洪量在1985年以后开始表现出明显的下降。

（2）通过Mann-Kendall非参数检验法对石栈道水文站1957～2016年洪峰流量和1日洪量序列变化规律进行了分析。结果表明：浊漳河北源洪峰流量在1971年发生了突变，1日洪量在1974年发生了突变，均呈现显著的下降趋势。

（3）1957～2016年石栈道水文站洪峰流量和1日洪量变化过程线可看出，石栈道水文站洪峰流量和1日洪量变化规律基本一致，即大洪峰大洪量，小洪峰小洪量。通过矩法估计P-Ⅲ型分布函数的参数值，同时采用Kolmogorov-Smirnov进行检验，洪峰流量和1日洪量K-S统计检验值分别为0.063 3和0.133 5，显著水平0.05对应的临界值是0.172 3，检验结果均为0，通过检验，可认为洪峰流量和1日洪量均服从P-Ⅲ型分布。

（4）采用均方根误差评定Gumbel-Hougaard，Clayton和Frank Copula三种Copula函数拟合结果。结果表明，浊漳河北源石栈道水文站适合运用Gumbel-Hougaard Copula进行洪水峰量特征分析，拟合误差仅为0.300 5。

（5）基于G-H Copula函数研究分析洪峰、洪量联合分布下的联合重现期和同现重现期。结果显示，选取不同的边缘分布重现期得到联合分布重现期，边缘分布的重现期介于联合重现期与同现重现期之间。联合分布的两种重现期可以看作边缘分布的两种极端情况，可将联合分布的重现期作为实际重现期的区间估计。

参考文献：

[1] 唐建. 基于MK检验的天山山区近55年降水特征分析[J]. 甘肃水利水电技术，2019，7（1）：5-8.

[2] De MICHELE C，SALVADORI G.A Generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas[J]. Journal of Geophysical Research： Atmospheres， 2003， 108（D2）： 4067.

[3] 熊立华， 郭生练. 两变量极值分布在洪水频率分析中的应用研究[J]. 长江科学院院报，2004，21（2）：35-37.

[4] 唐建. 基于Copula函数的洪峰流量与洪水历时联合分布研究[J]. 中国农村水利水电，2017（2）：204-214.

[5] 何英，彭亮，郑淑文，等. 基于Copula函数的叶尔羌河流域洪水要素联合分布研究[J]. 中国农村水利水电，2019（4）：74-79.

[6] 刘章君，郭生练，许新发，等. 两变量洪水结构荷载重现期与联合设计值研究[J]. 水利学报，2018，49（8）： 956-965.

[7] 梁艳芹. 海河流域暴雨洪水演变趋势分析[J]. 南水北调与水利科技，2014（3）：180-185.

[8] 杨兴，赵玲玲，陈子燊，等. 中小流域洪峰流量与水位联合分布的设计洪水分析[J]. 水电能源科学，2019，（8）：43-46.

[9] 郭生练，闫宝伟，肖义，等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文， 2008，28（3）：1-7.

（编辑：李 慧）

Analysis of evolution law and combined frequency of flood peak and volume in northern source of Zhuozhang River of Shanxi Province

SONG Jiajia ， ZHANG Fangqi

（Institute of Architectural Design and Research，Taiyuan University of Technology，Taiyuan 030024，China）

Abstract：To study the flood characteristics in the northern source of Zhuozhang River of Shanxi Province， the daily discharge data of 60 years from 1957 to 2016 at the Shizhandao Hydrological Station in the basin were used to analyze the flood peak and maximum 1 day flood volume. Through Mann-Kendall nonparametric test method， the characteristics and evolution laws of flood peak and maximum 1 day flood volume at the Shizhandao Hydrological Station were revealed， and the combined frequency of flood peak volume in the northern source of the Zhuozhang River was studied by Copula function. The results showed that the peak discharge and maximum 1 day flood volume were in an obvious decreasing trend; in the time series， the peak flood discharge has a significant decreasing trend after 1971， and the 1 day flood volume has a significant decreasing trend after 1974; Gumbel-Hougaard Copula function can well fit the correlation between the peak and volume of the flood in the northern source of the Zhuozhang River. The results can provide scientific basis for planning and risk assessment of water conservancy projects in the basin.

Key words： flood peak flow; maximum 1 day flood volume; Mann-Kendall test; Copula function;  northern source basin of Zhuozhang River