光的夫琅禾费衍射实验再研究

赵小侠，袁宇博，杨 迪，邹呈祥，王 浩，贺俊芳，王碧熙，王红英，付福兴

(西安文理学院 机械与材料工程学院，陕西 西安 710065)

光波是极高频率的电磁波(可见光波段频率ν：7.5×1014～4.1×1014Hz)，因此它的波长很短(可见光波段波长λ：390～760 nm，1 nm=10-9m)。相对于日常所见的宏观物体来说，光波的波长实在是太小了，根据光的衍射条件，光在行进中遇到的障碍物的尺寸与光的波长可比拟才可以观察到光的衍射现象。因此实际生活中，光虽然在传播过程中具有波动性，但是在实际问题的处理中均以几何光学即光在均匀介质中是直线传播的，不考虑光遇到障碍物的衍射现象。在考虑光的波动性，讨论光遇到障碍物的衍射现象时，根据光源与障碍物以及观察屏的远近，又人为的分为菲涅尔衍射(近场衍射)和夫琅禾费衍射(远场衍射)。本文利用惠更斯-菲涅尔原理与基尔霍夫标量衍射理论[1-5]在分析夫琅禾费衍射光强的基础上，设计了远场的夫琅禾费衍射实验光路，对不同形状的衍射物的夫琅禾费衍射光强进行了研究。使衍射的理论公式更为形象，有利于对光的衍射规律的理解。

1 理论分析

根据惠更斯一菲涅尔原理得出的单缝夫琅禾费衍射光强[6]分布可知，单缝衍射的中央亮纹位置，由

sinu=0

(1)

决定，其中u=(πbsinθ)/λ，λ为单色光波长，b为单缝的宽度，θ为衍射角。

这样满足方程u0=(πbsinθ0)/λ

(2)

的方向，即衍射角sinθ0=0(衍射中央最大值的位置即透镜焦点F0处)，IPo是在透镜焦点F0处的光强：

Ipo=A2

(3)

其中A为振幅大小，这时衍射光强为最大值。

如果在透镜的物方焦平面上光源S有变动得到单缝衍射的光强公式普遍形式[7]，

(4)

其中IP为观察屏上任一点P的衍射光强，I0为焦点F0处的最大光强，φ为光源的方位角，θ0为衍射角。

胡柯[8]利用数值积分精确计算了各级明暗环衍射角、中央艾里斑与衍射图样中各级明环光强和各级明环峰值光强，并利用最小二乘法探讨了各级明暗环衍射角与相对光强随衍射级次的变化规律，得到圆孔夫琅禾费衍射光振幅径向分布的积分表达式的相对光强分布：

(5)

其中IP是观察屏上任一点P的光强，I0为中央艾里斑光强度，EP和E0分别为P点和中心处的振幅强度，x′=x/R为积分路径，R为圆孔的半径，x为选取的直条形面元距中心的距离，m=kRsinθ，k为波数，θ为衍射角。

由公式(4)和(5)理论上可以分析得到衍射屏上各处的单缝和圆孔衍射光强，为了使上面衍射光强分布直观，设计了下面图1所示的夫琅禾费衍射光路图，将不同形状和大小的障碍物作为衍射物进行了实验研究。

2 夫琅禾费实验光路设计

夫琅禾费实验实物光路图见图1。

图1 夫琅禾费衍射实验实物光路图

图1中从左到右依次为：(1)532 nm的激光器作实验光源；(2)圆形可调衰减器；(3)空间滤波器；(4)焦距为100.0 mm的准直透镜；(5)可变光阑；(6)衍射物；(7)焦距为100.0 mm的透镜；(8)CMOS数字相机，通过数据线与电脑连接。

搭建调试好如上图1的夫琅禾费衍射光路后，让经前面光路准直后的平行光投射在衍射物上，经过聚焦透镜7的变换，将CMOS相机放置在透镜焦平面上，通过调节数字摄像机CMOS的成像参数，把采集到的衍射图样通过数据线传输到电脑中进行观察。

3 不同衍射物的夫琅禾费衍射实验结果及分析

3.1 夫琅禾费单缝衍射实验

图2所示的是衍射物6为不同宽度的单缝的夫琅禾费衍射实验图，图中左边为CMOS相机采集到的衍射图样，右边为经过软件处理后的衍射图样的光强分析图。

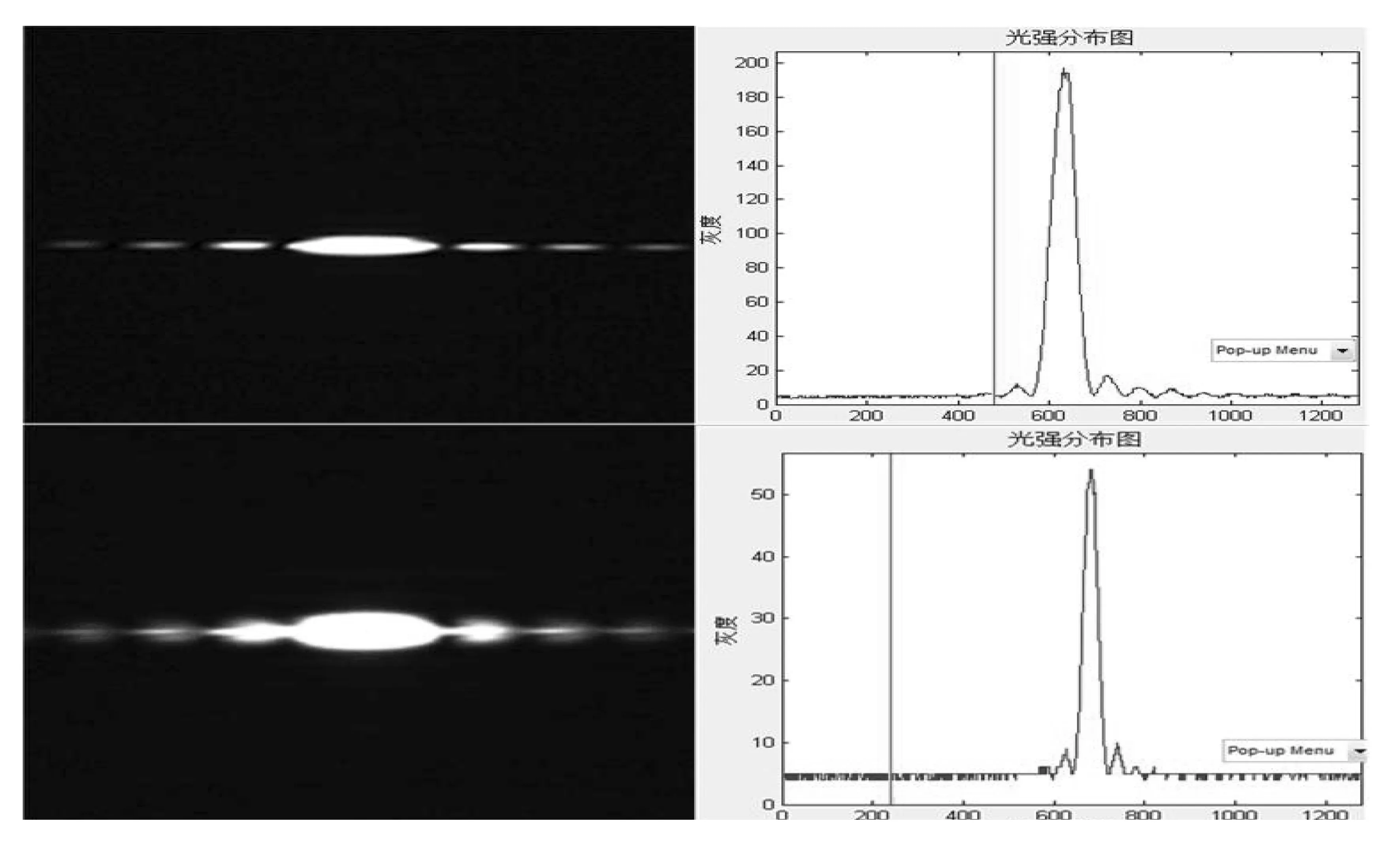
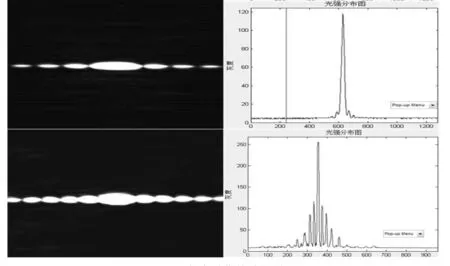
图2 夫琅禾费单缝衍射图

图2左边从上到下狭缝宽度依次为150 μm、250 μm、350 μm、450 μm。图中右边为经过软件处理的对应单缝缝宽时衍射光强分布。从图2可以看出亮纹最大光强值是不相等的，中央最大值的光强是最大，等于其他亮条纹亮度的二倍。随着单缝宽度b的增大，衍射现象变得不明显，各级次极大光强逐渐增大。

3.2 夫琅禾费圆孔衍射实验

图3为衍射物6为不同尺寸的圆孔时的夫琅禾费衍射实验图。图3左边为CMOS相机采集到的衍射图样，右边为经过软件处理后的衍射图样的光强分析图。

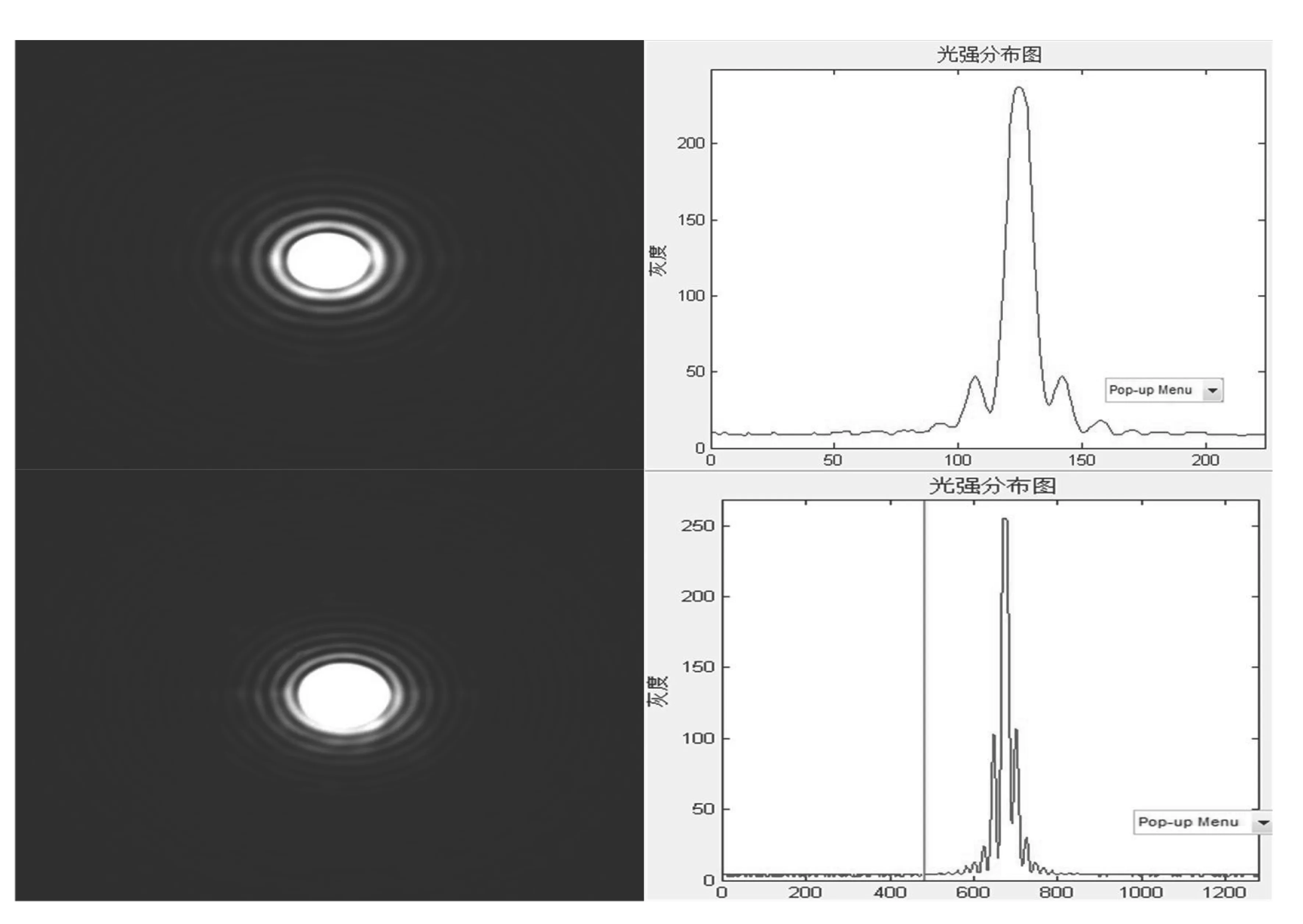
图3 夫琅禾费圆孔夫琅禾费衍射图

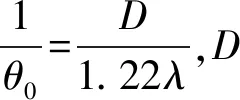
比较图2和图3夫琅禾费单缝衍射和圆孔衍射，可以看出这两者在定性方面是一致的，圆孔衍射只有形状和因数1.22不同。中间零级光强较强；除中间亮斑外，光强沿径向，呈现强弱相间分布，并且随着极径增大其峰值逐渐减小。

3.3 夫琅禾费正六边形衍射实验

图4为衍射物6为不同尺寸的正六边形的夫琅禾费衍射图样，图4左边为CMOS相机采集到的衍射图样，右边为经过软件处理后的衍射图样的光强分析图。

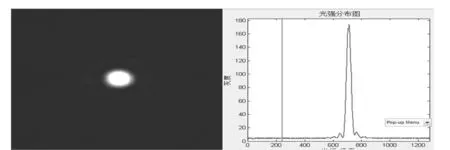
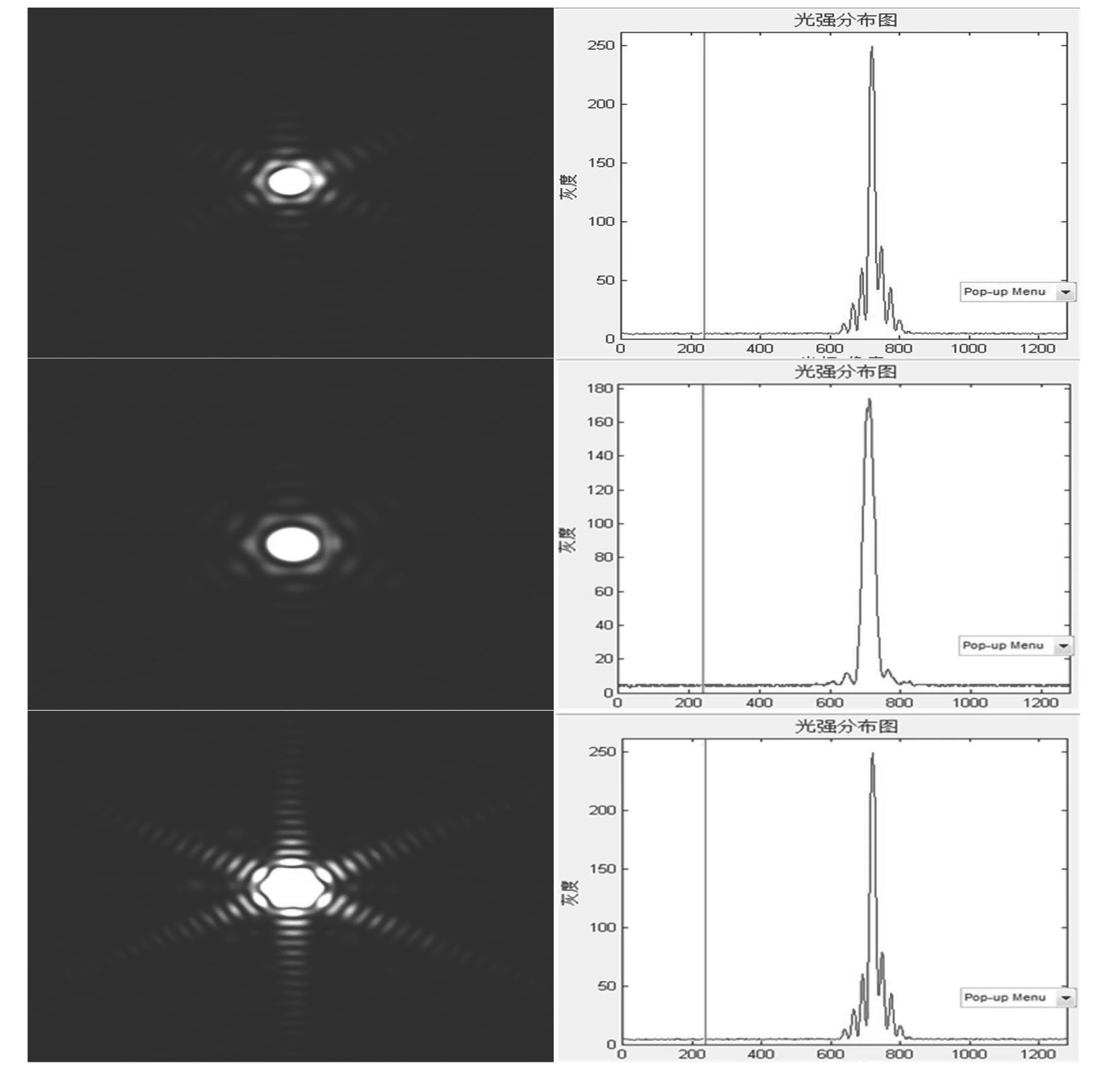
图4 夫琅禾费正六边形夫琅禾费衍射图

图4左边从上到下六边形内切圆半径依次为150 μm、250 μm、350 μm、450 μm。由上图可以清楚地看到当六边形衍射图样，与理论分析的规律一致[9]。当六边形内切圆半径较小时的衍射图样与圆孔衍射相似，随着内切圆半径的增大，六边形各边的衍射逐渐明显，从衍射图样可以看出六边形的每一边对应的衍射图样相当于一个单边衍射[10]，六边形每一边的衍射图样中也存在许多次极大值，这是由于在其他方向上的衍射光线叠加后光强很弱所造成的。当正偶数多边形的边数增加时，每组相对的平行边的同级衍射明条纹会逐渐靠近，可以推测当边数趋于无穷大时衍射图样应该与圆孔衍射的图样一致。

3.4 夫琅禾费单边衍射实验

为了验证对六边形衍射图样的猜想，随后又做了夫琅禾费单边衍射的实验，将衍射物6换为单边，经CMOS相机采集到的单边夫琅禾费衍射图样如图5所示。

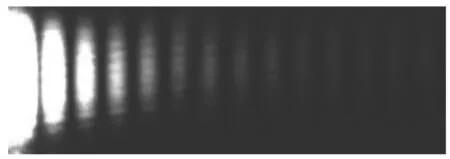
图5 夫琅禾费单边衍射的衍射图样

图5的夫琅禾费单边衍射的衍射图样，与上述六边形中一个边的衍射图样是一致的，也与下面图6所做的正方形的夫琅禾费衍射图样中单边衍射图样一致。

3.5 夫琅禾费正方形衍射实验

图6为衍射物6为不同尺寸的正方形的夫琅禾费衍射图样。

图6 夫琅禾费正方形衍射图样

图6中从左到正方形边长依次为150 μm、250 μm、350 μm、450 μm。当正方形边长比较小时，夫琅禾费衍射图样模糊，且接近于圆孔衍射，随着正方形边长的增大，可以清楚地看到正方形衍射图样与理论分析一致[11，12]，且衍射条纹也变得越来越清晰。正方形每一边都呈现的是单边直边衍射现象。中央亮纹强度最大，中央亮纹宽度是各次级大亮纹宽度的2倍，所以中央亮纹光强是相对的两边直边衍射的叠加。其他亮纹强度随着级数的增加，迅速减弱，这与图5的单边衍射图样是一致的。

3.6 夫琅禾费正三角形衍射实验

图7为衍射物6为正三角形的夫琅禾费衍射图样。

图7 夫琅禾费三角形衍射图样

图7为衍射物是正三角形的夫琅禾费衍射图样，从左到三角形内切圆直径依次为150 μm、250 μm、350 μm、450 μm。由图中可以清楚看到当三角形外切圆直径值很小时，衍射图样变得模糊。随着三角形内切圆的直径增大，衍射图样变得清晰可见。三角形各边显示单边衍射图样与前面讨论一致，当光通过三角形两边夹角处时，因为满足光的干涉条件，在两边夹角处又同时发生了光的干涉。所以一幅三角形夫琅禾费衍射图样中既有单边衍射，又有两边之间的干涉，是干涉和衍射同时存在，这正是光学的魅力所在。

4 结 语

本文在分析单缝和圆孔夫琅禾费衍射光强的基础上，设计了夫琅禾费衍射实验光路，对不同单缝宽度的单缝、不同圆孔直径衍射物的夫琅禾费衍射光强进行了定性和定量研究。使衍射的理论公式更形象，有利于对衍射规律的理解。随后又实验了不同尺寸的六边形、正方形衍射物的夫琅禾费衍射图样，根据所得的衍射图样猜想图样中的衍射含有单边直边衍射，接着实验得到单边夫琅禾费衍射的衍射图样，单边衍射图样能够很好地解释六边形和正方形的夫琅禾费衍射图样。这样可以把单缝夫琅禾费衍射图样看成是两个间距与波长可比拟的相互平行的两个单边衍射之间的干涉图样，正方形夫琅禾费衍射图样看成是在正方形两相对边间的单边衍射之间的干涉图样和两对相互垂直方向上的干涉图样的非相干叠加的结果。由图4和图7的正六边形和正三角形夫琅禾费衍射图样可以看出他们是各自的单边衍射和各边间的干涉共同作用的结果，对于正六边形来说相邻两边夹角为120°，等边三角形的相邻两边间的夹角为60°，因此对于相邻的两边间的单边衍射之间的干涉来说，三角形的光强在平行方向上的分量大于六边形，这也是三角形衍射图样中相邻两边间干涉图样比六边形衍射图样中相邻两边间干涉图样较为明显的原因。对多边形衍射图样的分析可以看出是他们的衍射图样都可以看成是各边的单边夫琅禾费衍射的衍射图样和相邻两边间干涉的共同作用结果。