Crossed products for Hopf group-algebras
2021-10-21YouMimanLuDaoweiWangShuanhong
You Miman Lu Daowei Wang Shuanhong
(1School of Mathematics and Information Science, North China University of Water Resources and Electric Power, Zhengzhou 450045, China)(2Department of Mathematics, Jining University, Qufu 273155, China)(3School of Mathematics, Southeast University, Nanjing 211189, China)
Abstract:First, the group crossed product over the Hopf group-algebras is defined, and the necessary and sufficient conditions for the group crossed product to be a group algebra are given. The cleft extension theory of the Hopf group algebra is introduced, and it is proved that the crossed product of the Hopf group algebra is equivalent to the cleft extension. The necessary and sufficient conditions for the crossed product equivalence of two Hopf groups are then given. Finally, combined with the equivalence theory of the Hopf group crossed product and cleft extension, the group crossed product constructed by the general 2-cocycle as algebra is determined to be isomorphic to the group crossed product of the 2-cocycle with a convolutional invertible map of the 2-cocycle. The unit property of a general 2-cocycle is equivalent to the convolutional invertible map of the 2-cocycle, and the combination condition of the weak action is equivalent to the convolutional invertible map of the 2-cocycle and the combination condition of the weak action. Similarly, crossed product algebra constructed by the general 2-cocycle is isomorphic to the Hopf π-crossed product algebra constructed by the 2-cocycle with a convolutional invertible map.
Key words:Hopf π-algebra; cleft extension theorem; π-comodule-like algebra; group crossed products
Hopf crossed products were introduced independently by Yukio et al.[1]and Blattner et al.[2]as a Hopf algebraic generalization of group crossed products. In particular, a Hopf crossed product is, in fact, always a Hopf cleft extension, provided that the cocycle that appeared in a Hopf crossed product is convolution-invertible[3-5].
Hopf group-algebras were related to homotopy quantum field theories, which are generalizations of ordinary topological quantum field theories[3,6-8]. In 2007, Wang et al.[9-11]introduced group smash products of Hopf group-algebras. Group crossed products of Hopf group-coalgebras were introduced[12-13]. Other related works can be found in Refs.[14-17].
In this article, we introduce and study the notions of a group crossed product and a group cleft extension. We then characterize group crossed products by the group cleft extension. Finally, we prove the equivalences of the group crossed products for the Hopf group-algebras.
1 Group Cleft Extensions and Existence of Group Crossed Products
Definition1LetA=({Aα}α∈π,Δ,ε) be a Hopfπ-algebra with the bijective antipodeSandJas algebra. We say thatAacts weakly onJif there exists a family of maps:
a⊗xa⇀αx, ∀α∈π,a∈Aα,x∈J, such that
1) 1α⇀x=x, ∀x∈J;α∈π;
2)a⇀α(xy)=(a(1,α)⇀αx)(a(2,α)⇀αy), ∀a∈Aα,x,y∈J;
3)a⇀α1J=εα(a)1J, ∀x∈J.
Furthermore, ifJis anAαmodule for eachα∈πand satisfies 2) and 3), we callJa leftπ-A-module-like algebra.
Definition2LetA=({Aα}α∈π,Δ,ε) be a Hopfπ-algebra andJa leftπ-A-module-like algebra. Letχα,β:Aα#Aβ→Jbe a family ofk-linear maps and suppose thatχis an invertible map. Suppose thatJacts weakly on eachAαwithα∈π. For anyα∈π, there is aπ-crossed productJ#χAαwith the multiplication given by (x#αa)(y#βb)=x(a(1,α)⇀αy)χα,β(a(2,α),b(1,β))#αβa(3,α)b(2,β), for alla,b∈Aα,Aβ,x,y∈J,α,β∈π, and the unit is 1J#1α.
Proposition1With the above notations,J#χAαis a Hopfπ-crossed product if and only if the following conditions hold: ∀a∈Aα,b∈Aβ,c∈Aγ,∀α,β∈π, andx,y∈J.
χα,β(a,1β)=χα,γ(a,1γ)=εα(a)1J
(1)
χα,β(a(1,α),b(1,β))χαβ,γ(a(2,α)b(2,β),c)=
(a(1,α)⇀αχβ,γ(b(1,β),c(1,γ)))χα,βγ(a(2,α),b(2,β)c(2,γ))
(2)
χα,β(a(1,α),b(1,β))(a(2,α)b(2,β)⇀αβx)=
a(1,α)⇀α(b(1,β)⇀βy)χα,β(a(2,α),b(2,β))
(3)
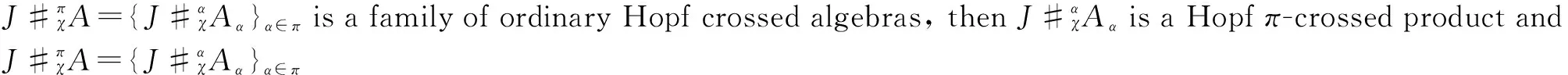
Remark11) Ifπ=1, the Hopfπ-crossed product is then the ordinary Hopf crossed product.
2) If we takeχα,β(a,b)=εα(a)εβ(b)1J, ∀α,β∈π,a∈Aα,b∈Aβ, the Hopfπ-crossed product becomes the Hopfπ-smash product.
LetAbe a Hopf algebra. For anyα∈π, denoteδαas the one-dimensional linear space generated byα. Then we have a Hopf group algebraH={Hα=A⊗δα}α∈πwith the structure (a⊗α)(1,α)⊗(a⊗α)(2,α)=a1⊗α⊗a2⊗α,εα(a⊗α)=ε(a),Sα(a⊗α)=S(a)⊗α-1.
IfJ#σAis a crossed product withσ:A⊗A→J. Define
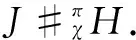
Definition3LetJbe a leftπ-Aα-module-like algebra.
1) We say thatH⊂Jis aπ-Aα-extension ifJis a rightπ-Aα-comodule algebra with a family ofk-linear mapsρ={ρα:J→J⊗Aα},
JcoAα={x∈J|ρα(x)=x⊗1α∈J⊗Aα, ∃x∈J, ∀α∈π}
which is called aπ-subalgebra of the rightπ-co-invariants.

εα(a)1J∀a∈Aα,α∈π
Lemma1LetH⊂Jbe aπ-Aα-cleft extension with a rightπ-Aα-comodule structure map:ρ={ρα:J→J⊗Aα} viaxx(0,0)⊗x(0,α)forα∈πand aπ-Aα-cleft structure map:γ={γα:Aα→J}α∈πsuch thatγα(1Aα)=1Jwith We then have

Proposition3LetH⊂Jbe aπ-Aα-cleft viaγ={γα:Aα→J}α∈πsuch thatγα(1Aα)=1Jwithα∈π. Then, there is a Hopfπ-crossed product with a weak action ofAαonJgiven by
and a family of convolution-invertible mapsχ={χα,β:Aα⊗Aβ→J}α,β∈πgiven by
∀a∈Aα, ∀b∈Aβ

ProofFirst, we compute forx∈J,a∈Aα,
⊗Sα-1(a(3,α-1)))=a⇀αx⊗1Aα∈J⊗Aα
and thus,a⇀αx∈H=JcoAα. Furthermore, it is easy to see that Definition 1 2) and 3) hold.
Similarly, we can prove thatχ={χα}α∈πhas values inA. In fact, ∀a,b∈Aα,Aβ,
ρα(χα,β(a,b))=ραγα(a(1,α))ραγβ(b(1,β))·

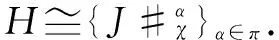
Finally, it is easy to check thatΦ={Φα}α∈πis a leftπ-J-module-like map and is a rightπ-Aα-comodule map.
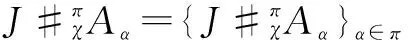

To check thatνis a right inverse forγis more complicated. By a computation similar to the above, we have
a(5,α))]χα(α(2,α),S(a(3,α)))#1Aα
(4)
and hence,νis a right inverse forγif and only if
(5)
Sinceχ={χα,β:Aα⊗Aβ→J} is invertible, Eq. (2) gives

(a(3,α),b(3,β)c(3,γ))=a⇀αχβ,γ(b,c)
(6)
for anya∈Aα,b∈Aβ,c∈Aγ.

εα(a)εβ(b)εγ(c)1J
(7)
Hence, from Eq. (7), we obtain
(8)
We may now verify Eq. (6) using Eq. (8):
By Proposition 3 and Proposition 4, we can now get the main result of this section as follows.
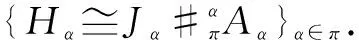
2 Equivalences of Group Crossed Products
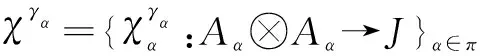

The proof is clear.
Theorem2LetJbe a Hopfπ-algebra,Aαa family of coalgebrasA={Aα,mα,1Aα}α∈π, andγ={γα:Aα→J}α∈πa family of convolution-invertible linear maps. Ifχ={χα:Aα⊗Aα→J}α∈πis a family ofk-linear maps, we then have the following assertions with the above notationsχγαfor anyα,β∈π:
2)χsatisfies Eq. (1) if and only ifχγsatisfies Eq. (1);
3) (χ,⇀) satisfies Eq. (2) if and only if (χγ,⇀γ) satisfies Eq. (2);
4) If(χ,⇀) satisfies Eq. (2), (χ,⇀) satisfies Eq. (3) if and only if (χγ,⇀γ) satisfies Eq. (3);


3) If (χ,⇀) satisfies Eq. (3), then
(a(1,α))⇀γα(b(1,β)⇀γβx))χγαα,β(a(2,α),b(2,β))=
γα(a(1,α))(a(2,α)⇀γβ(b(1,β)))χα,β(a(3,α),b(2,β))

Conversely, we get it from Lemma 2.
4) If (χ,⇀) satisfies Eq. (2) and Eq. (3), then, fora∈Aα,b∈Aβ,c∈Aγ,
γα(a(1,α))(a(2,α)⇀[γβ(b(1,β))(b(2,β)⇀γγ(c(1,γ)))·

γα(a(4,α))(a(5,α)⇀γβγ(b(5,β)c(4,γ)))χα,βγ(a(5,α),b(6,β)c(5,γ))·
2) and 5) of Theorem 2 are clearly proved.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Drivers’ fixation transfer characteristics in urban tunnels
- Performance analysis of a novel tobacco-curing system with a solar-assisted heat pump
- Sustainability of health information exchange platform based on information cooperation
- Comparative study of low NOx combustion optimization of a coal-fired utility boiler based on OBLPSO and GOBLPSO
- Concept and evaluation method of equipment system of systems contribution rate
- TOD typology: A review of research achievements
